高中数学函数解题思路多元化的方法分析

唐菊香

(江苏省扬州市邗江区公道中学 225000)

新课改标准下，高中学生在学习期间逐步意识到函数解题的重要性，多元化解题思路成为影响学生学习效果的关键点，关联学生综合能力的培养.在多元化解题过程中，不只是可调动学生学习主观能动性，还可使得学生数学素养得以发展，为学生全面成长奠定基础.如何带领学生掌握函数解题多元化方法，拓展学生学习视野是至关重要的课题，为此笔者给出下列建议.

一、高中数学函数解题思路多元化概述

在高中函数学习过程中，为了保障学生逻辑思路清晰化，学生要以客观的视角出发，在处理函数问题时，了解计算方法，可是不知道解决问题的真实含义.因此在训练解题思路过程中，要深层次探索解题问题的意义，多元化解题方法可实现这一个目标，调动学生创新思维，在问题解决期间掌握多元化处理问题的思路，提高学生解决问题效率，所以多元化解题方法的运用是至关必要的.学生学习函数之后，可初步了解函数代表变量y以及变量x之间的关系，高中阶段涉及的函数知识比初中阶段的函数知识更加繁琐，重点是基于集合变量，计算对应关系.解决问题时要分析函数相关概念，了解变量之间的关联，由此优化现有的解题形式.在具体解决问题期间，没有完全明确概念知识条件下就参与训练，取得的结果是不理想的，因此在日常学习与教学中，要全面掌握函数知识，以基础知识为主探索解决问题的更多方法，加强学生对知识点理解与掌握，强化学生综合能力和数学素养发展.

二、函数解题思路多元化，形成发散思维

在处理数学问题过程中，也就是分析数量问题，研究题目内多个元素之间的关系与具体结构，挑选切合实际的处理问题方法.总体而言，学生参与训练为了获取解决问题的思路，若局限在一个解决问题方式上，学生自身的思维会相对被动化，信息处理时间不足，对应的思考空间也会相对封闭.可是因为多种因素的影响，大多数情况下教材中的例子仅仅存在单一解决问题的方法，引出学生思维受到限制的结果，降低学生发散思维培养效果，降低知识网络建立有效性.所以要适当组织学生参与一题多解的学习活动，一方面保证学生对问题进行优化，另一方面延伸学生思维空间，找到思维发散的具体方向，保证学生更好的学习与思考.

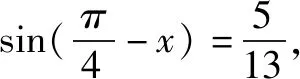
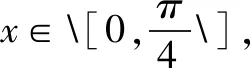
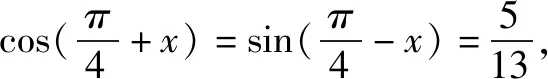
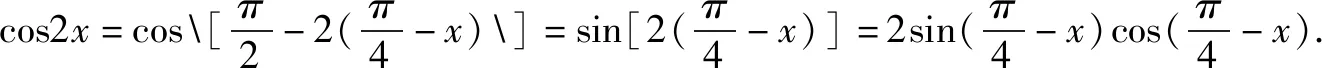
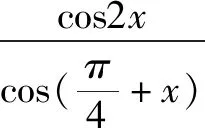
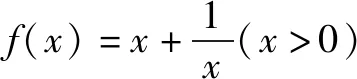
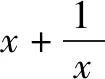
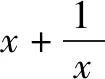
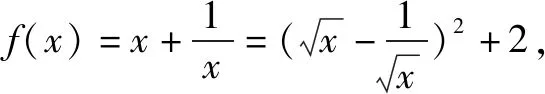
由此，处理数学函数问题的方法是灵活且多样的，技巧性比较强，问题的分析成为处理问题的关键点，熟练运用解决问题方法是要点，联想计算问题答案是必要的手段，科学旋转与公式变形都是促使学生思维发散运作的媒介.所以要组织学生善于使用发散思维，找到思维定势的突破点，增强学生研究问题能力，长时间训练之后势必会促使学生思维更为开放.

三、函数解题思路多元化，形成逆向思维

结合个体的思维方式差异，思维过程涉及的方向性包含正向思维以及逆向思维，两者互相矛盾与冲突，可都是比较重要的思想.然而现阶段高中阶段的数学教学内容缺少逆向思维的渗透，在一定程度上影响学生逆向思维形成，要想通过正向思维对问题进行处理会产生困难，所以要探索另外处理问题方式，明确逆向思维的使用思路，使得学生在有限时间内通过逆向思维简化问题.

例3若Sn代表等比数列前n项和，已知S3、S9以及S6之间成等差数列，证明：b2、b8与b5也是等差数列.

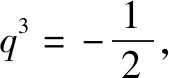
基于此，对函数问题进行多元化思考，改变以往的解决问题顺序，引进逆向思维模式，更加透彻的分析问题和解决问题，树立学生学习信心，调动学生学习积极性，在学生得到良好学习体验同时强化学生逆向思维发展.

四、函数解题思路多元化，形成创新思维

一题多解，即解题思路多元化，能够改变一组命题的结论，关联着解决问题的方法，师生对命题与命题的形式加以分析，增强解决问题的综合水平，活跃学生大脑思维，不断调动学生创新力，在解题思路多元化操作之下，帮助学生形成创新思维.

例4 计算不等式：3<|2x-3|<5.

解法1 对不等式进行变形：3<|2x-3|<5可替换3<|2x-3|并且|2x-3|<5，所以3

解法2 按照绝对值基本定义，分类进行讨论：

(1)在2x-3≥0时，3<|2x-3|<5等价为3<2x-3<5，即3

(2)在2x-3<0时，3<|2x-3|<5等价为-1

解法3 通过等价命题法，3<|2x-3|<5替换成3<2x-3<5或者-5<2x-3<-3，得到{x|3

基于此，适当引进思维创新方法，从多个角度上思考和处理问题，体现数学问题的灵活多变性，启迪学生思维，使得学生思维得以创新与发展，强化高中学生学习效率.

综上所述，高中数学教材中，函数知识是比较重要的，存在逻辑性与多变性，师生应该立足于函数问题的本质，从函数概念出发，充分挖掘解决函数问题的多元化方法与思路，在发散思维、逆向思维与创新思维培养之下，不断提高学生解决问题的速度，丰富学生数学知识面，加深学生对知识点印象和感知，由此确保高中数学课程高效率进行.