一道2020年高考圆锥曲线试题的探究与推广
2021-08-05喻秋生
数理化解题研究 2021年10期
喻秋生
(广东省深圳实验学校高中部 518055)
一、问题的提出
2020年高考(北京卷)第20题是求值问题,该试题如下:
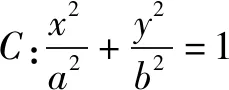
(1)求椭圆C的方程;
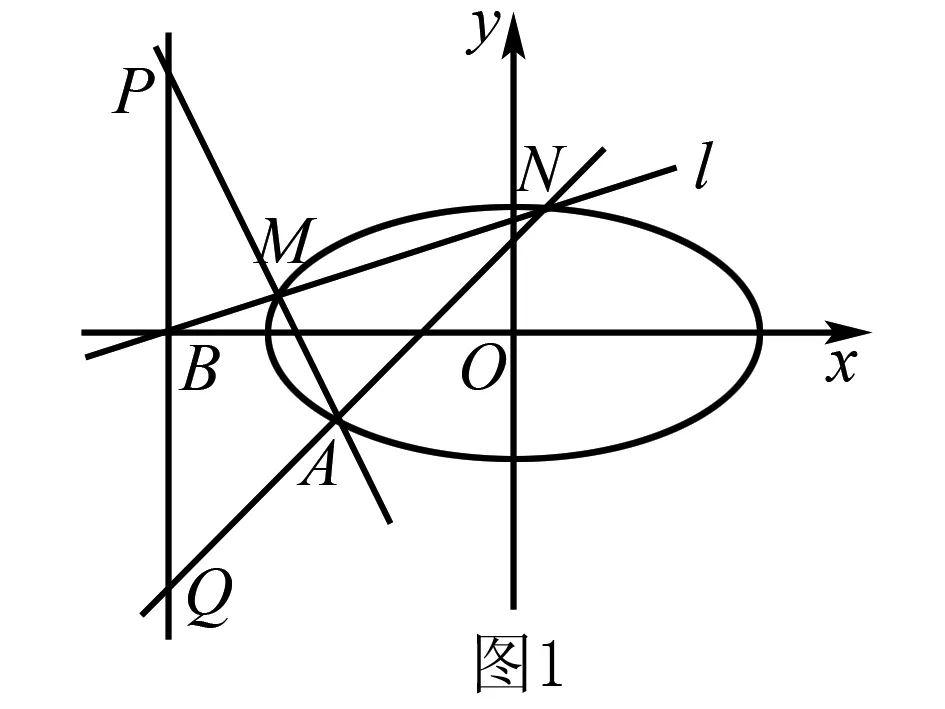
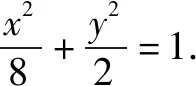
(2)如图1,直线l的斜率存在,设直线l的方程为y=k(x+4),
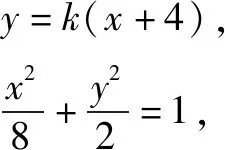
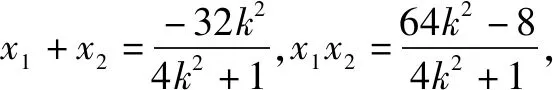
把y1=k(x1+4),y2=k(x2+4)代入上式化简,得
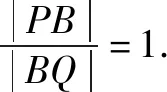
在这道试题中,椭圆C是给定的椭圆,点A、B分别是椭圆C、x轴上的特殊点,通过计算发现点B为PQ的中点.如果椭圆C是任意的椭圆,点A、点B分别是椭圆C、x轴上的任意点,是否仍然有对任意过点B的直线l,都使得点B为PQ的中点这一结论呢?
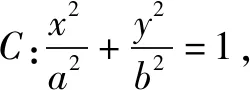
二、问题的探究
当直线l垂直于x轴且与椭圆有交点时,点P,Q即为M,N,点B为PQ的中点.
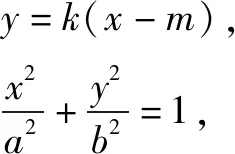
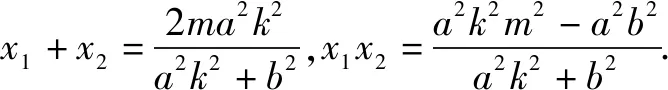
①
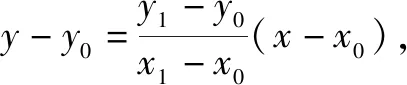
∵m-x0≠0,2y0,m-x0为常数,
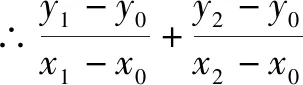
∵y1=k(x1-m),y2=k(x2-m),
②
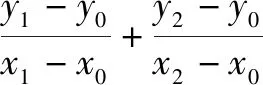
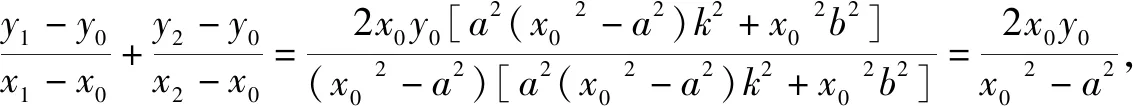
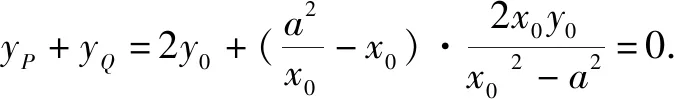
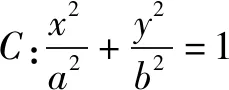
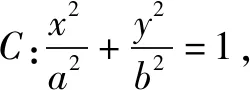
在结论1中,点B在x轴上,如果点B在y轴上,可以得出下面的结论,证明过程略.
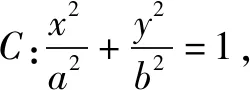
在圆中,经研究也有类似的结论:
结论3 已知圆C:x2+y2=r2,点A(x0,y0)在圆C上,过点B(m,0)(m≠x0)的动直线l与圆C交于M,N,直线MA,NA分别交过点B且垂直于x轴的直线于点P,Q.当且仅当mx0=r2,即直线AB为圆C的切线时,点B为PQ的中点.
三、问题的推广
如果曲线C为双曲线或抛物线,经研究也有类似的结论:
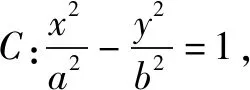
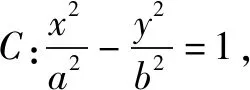
结论6 已知抛物线C:y2=2px,点A(x0,y0)在抛物线C上,过点B(m,0)(m≠x0)的动直线l与抛物线C交于M,N,直线MA,NA分别交过点B且垂直于x轴的直线于点P,Q.当且仅当m+x0=0,即直线AB为抛物线C的切线时,点B为PQ的中点.
上面三个结论的证明与结论1的证明类似,证明过程略.
