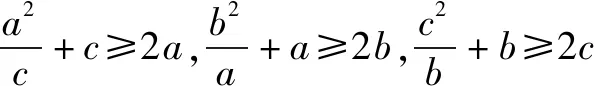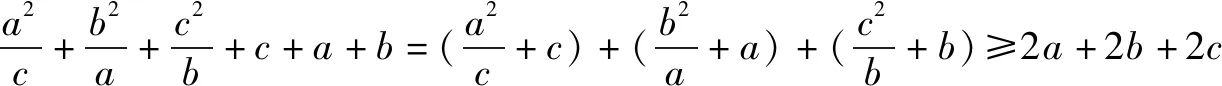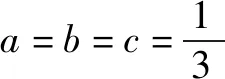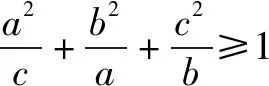基于核心素养下对基本不等式的再思考
2021-08-05杨伟达
数理化解题研究 2021年10期
杨伟达
(广东省广州市花都区第二中学 510800)
新教材将基本不等式放入高中数学第一册第二章,成了一线数学教师对新教材教学的热门话题,其意义深远,即突显出基础性、实用性、技巧性,又能够进一步提升学生的运算求解能力和转化与化归能力.下面是笔者对一些关于基本不等式的数学问题进行剖析,旨在提高学生的数学核心素养.
一、和与积
和与积是天生一对孪生兄弟.缺了谁,就找谁﹒如果和为定值,就要想办法找积的形式;如果积为定值,就要想办法找和的形式.在运用“和与积”时,必须满足“一正、二定、三相等”,若发现不符合三个条件时,就要进行变形,运用基本不等式即可.
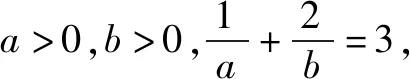
分析已知条件是和的形式,和为定值求积的最大值.观察、发现直接运用基本不等式即可.
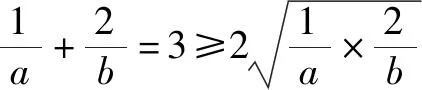
二、倒数和
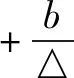
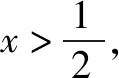
分析观察、发现倒数和的两项乘积不是定值,不能直接运用不等式,此时需要对倒数和进行变形,直到乘积为定值时运用基本不等式即可.
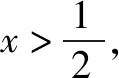
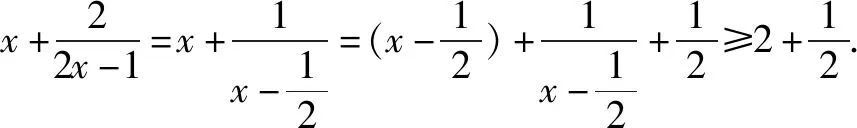
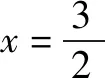
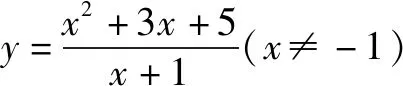
分析本题看似与不等式无关,实则可以通过拆分变为倒数和的形式,然后再运用基本不等式求解.
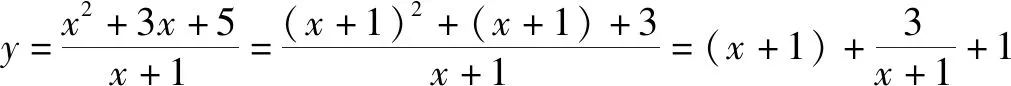
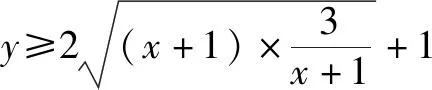
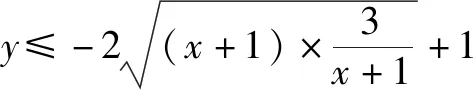
三、整式和与分式和
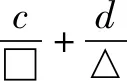
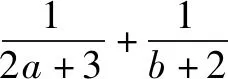
分析本题是整式和为定值求分式和的最值问题.解决办法:整式和乘以分式和﹒笔者观察、发现分式中的两分母之和与已知条件的定值不吻合,所以先将分式进行变形,后再将整式变形即可.
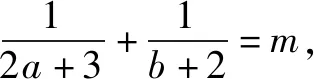
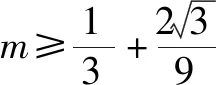
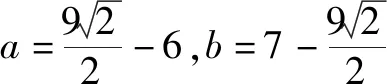
例5 已知a>0,b>0,a+3b=5ab,则3a+4b的最小值是( ).
分析将题设条件化简为分式和为定值的形式.笔者发现原问题是分式和为定值求整式和为最值的数学问题.解决办法:整式和乘以分式和后用基本不等式即可.
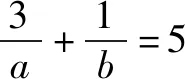
不妨设3a+4b=m,且a>0,b>0,则有
即5m≥25 解得m≥5,故选C﹒
四、整式和与整式和
已知整式和为定值求另一个整式和的最值.解决办法:分离后找配对.即配添分离,运用基本不等式即可将问题解决.
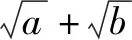
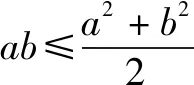
解因为a>0,b>0且a+b=1
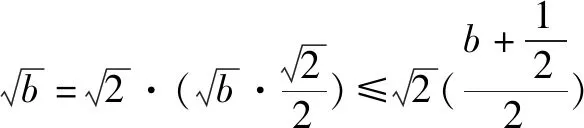
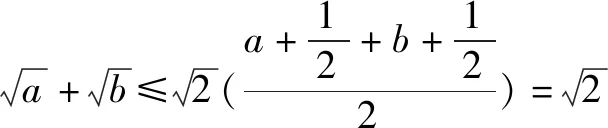
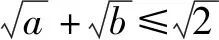
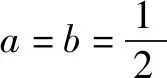
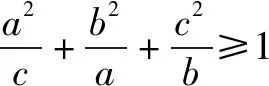
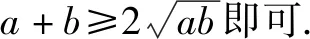
解a>0,b>0,c>0