行进中发现 反思中优化——以四道解三角形试题为例

郑 良

(安徽省合肥市第四中学 230000)

学习数学离不开解题，解题只是学习数学的有效手段而不是最终目的.解题需要且行且思，但离不开必要的基础知识、基本技能、解题经验，通过解题可以促进学生的观察能力、分析能力、表达能力的全面提高.解题的切入角度反映出学生思维的敏感性，预设方向取决于学生的解题经验，遇到困难时的思维转换体现出学生思维的深度，方法的选择与优化反映出学生思维的广度、深度与高度.解题的效率是学生数学综合素养的体现.下面以四道解三角形试题为例，谈谈解题过程的关键点，以期能对大家有所帮助.

一、分类与整合中优化

这四个结论中一定成立的个数是( ).

A.1 B.2 C.3 D.4

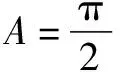
结合题意可知，②③④一定成立，答案为C.

二、不同视角中优化

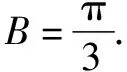
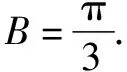
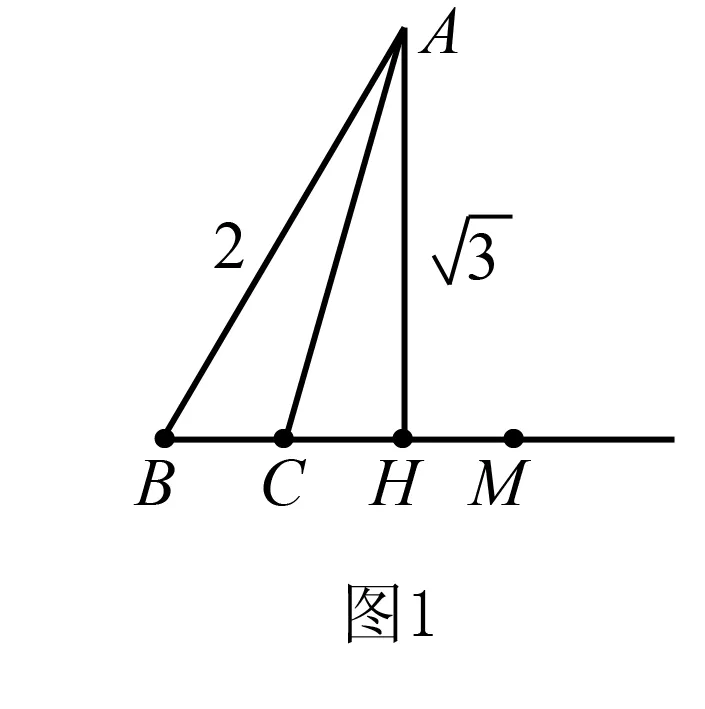
点评本题为2018年高考数学北京卷文科第14题，从以上解题过程可以看出，∠B的确定不受条件“∠C为钝角”的约束.解法1以问题为引领构建目标关于自变量∠C(题设隐性给出了∠C的范围)的函数，转化为函数的值域问题；解法2采用迂回战术构建目标关于自变量∠A(可间接求出∠A的范围)的函数，使分式函数的分母更简洁；解法3(类比：在△ABC中，已知边b，c和角∠B，判定三角形的解的个数)以静制动、数形结合，让结论更加清楚直观.

三、从逻辑关系中优化

例3 在△ABC中，a,b,c分别为内角A,B,C的对边，若a+c=4，2sinB=sinA+sinC，则△ABC的面积的最大值为( ).

解法1 由2sinB=sinA+sinC，根据正弦定理，可得2b=a+c，所以b=2.

点评解法1先利用对勾函数的性质确定角B的取值范围，再构建S△ABC关于角B的函数(求解取值范围的通性通法)，转化为求函数的最大值问题；解法2基于最值的概念与问题的特殊性(正数构成的积函数，当各部分均取最大(小)值时，函数取得最大(小)值，反之未必成立).本题将ac与sinB作为S△ABC的两个部分，它们同时取最大值的条件成立.

四、从问题结构中优化

A.①③ B.①② C.①②③ D.①②③④

解析由题意，得2b2=a2+c2.

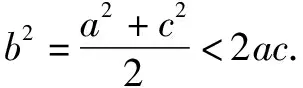
以上每道试题均涉及到问题的多个方面，例题只提到反思优化的几个方面，权当抛砖引玉，敬请批评指正.