基于北斗的μPMU相角同步测量精度问题的研究

魏文震，李 江，巩方伟，孙 磊，李 垚，王 欣

（1.国网山东省电力公司淄博供电公司，山东 淄博 255000；2.东北电力大学电气工程学院，吉林 吉林 132012）

0 引言

基于全球定位系统（Global Positioning System，GPS）的同步相量测量单元（Phasor Measurement Unit，PMU）已经在广域测量系统（Wide Area Measurement System，WAMS）中得到大规模应用［1-3］。由于GPS 信号受美国军方控制，一旦信号丢失，PMU将无法正常工作。随着我国北斗卫星导航系统（Beidou Navigation Satellite System，BDS）组网成功，考虑到PMU 体积庞大，价格昂贵，安装复杂等弊端，在配电网、低压系统中，研究基于BDS的微型同步相量测量单元μPMU 对提高系统的动态安全监控性能，确保配电网安全稳定运行具有重要意义。

高精度的相量测量是系统动态监测的关键［4-6］，因此BDS同步授时信息精确度直接影响相量测量的精度和可靠性。文献［7］对BDS信号覆盖范围、同步授时精度及工作可靠性进行了综合分析，证明了BDS 能确保异地被测相量的高度同步性，测量精度要比GPS 更高。在输电网中基于北斗与GPS 互备授时的PMU 早已有所研究［8-9］，通过对比北斗和GPS授时的同步相量测量试验结果验证了北斗授时的有效性。文献［10-11］通过相量表达式的推导和对发电机转子角测量原理的分析，分别讨论了授时偏差对P类和M 类PMU 量测的影响。然而，以上工作都是基于输电网PMU 开展的，对于配电网相量测量装置的研制及BDS的应用还很欠缺。

在之前研制的配电网μPMU 与故障录波装置的基础上，对时钟源进行更换［12］。在装置改进前，考虑到系统的环境、电磁干扰等因素会给BDS 的授时带来偏差，因此，BDS 授时偏差对量测精度的影响是改进能否成功的关键。分别从稳态和动态两方面推导了授时偏差下μPMU 量测相量的计算公式，分析了BDS 授时偏差对相量幅值和相角的影响规律。最后，通过MATLAB 对基于BDS 的μPMU 相量误差进行仿真，仿真结果验证了理论分析的正确性，采用BDS 作为时钟源可以有效提高原装置的相量测量精度，尤其是相角精度。

1 基于BDS的μPMU结构原理

基于BDS 的μPMU 结构原理如图1 所示。总体上可分为微控制器模块、综合电能监测模块、BDS 授时模块、过零检测模块、故障录波模块、人机接口模块和上位机通信模块等［8］。

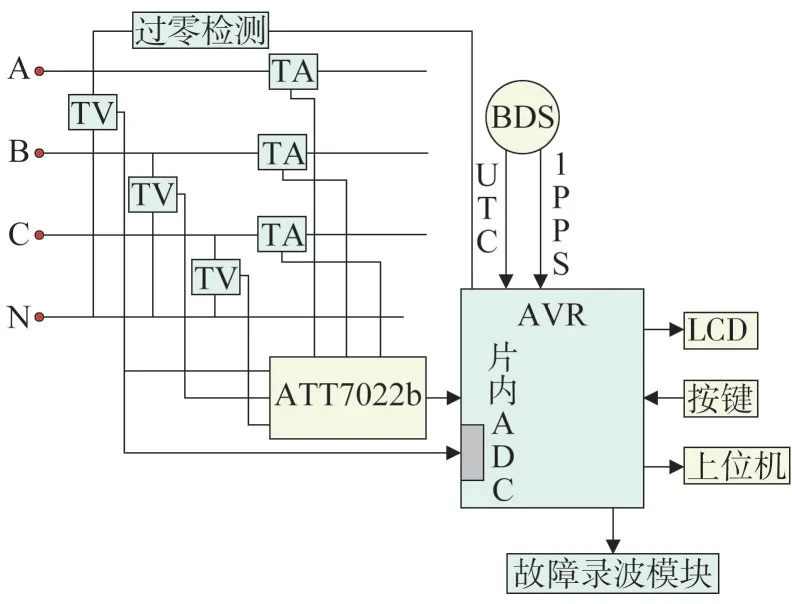
图1 μPMU的结构原理

三相四线制中的A、B、C 三相和零线N 经电压互感器TV 和电流互感器TA 接入到综合电能检测模块ATT7022b，经处理后将计量参数和校表参数传递到微控制器模块AVR 单片机，由BDS 提供精准授时，通过过零精测模块增强装置采样的抗干扰性。AVR 单片机与人机接口模块（LCD 液晶显示屏和按键）、上位机模块、故障录波模块相连，分别完成读数和设置、实时传输数据、故障数据保存等功能。

2 BDS时钟同步误差

由图1可见，μPMU 是在BDS提供的世界协调时间（Coordinated Universal Time，UTC）和1 秒脉冲（Pulse Per Second，PPS）下，对配电网中各安装节点的电压、电流进行同步测量，从而确保全网的测量结果具有同时性。因此，同步授时信息的精确度将直接影响相量量测的精度和可靠性。

2.1 BDS授时精度分析

BDS具有单向授时和双向授时2种授时功能，分别提供100 ns（单向授时）和20 ns（双向授时）的时间同步精度。因此，如果BDS的综合精度按50 ns计算，当系统信号频率为50 Hz时，其相角误差为0.000 9°，频率变化时的相角误差可以按（1+Δf）0.000 9°计，Δf为实际频率相对于额定频率的偏移量，可见，BDS作为μPMU 的异地同步测量时钟源具有比GPS 更高的精度［13-14］。时钟源授时精度到相角测量误差的转换为

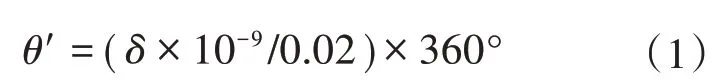
式中：δ为时钟源的授时精度，ns。

2.2 授时偏差的来源

当电力系统中μPMUs 的采样率为50 次/s 时，用Δt1、Δt2分别代表时间戳产生时经过精确时钟和偏差时钟的时间，Δt1=0.02 s，Δt2=0.02 s±ε，ε代表时间偏差［15］。Δt2略大于Δt1时产生的时间偏差如图2所示，Δt2略小于Δt1时产生的时间偏差如图3 所示。由图2、图3 中红色椭圆部分可见，偏差时钟在1 s 内产生的时间偏差比较明显。这是因为在偏差时钟下的相量测量结果并没有同步，导致此时的待测相量并不是在时间戳产生的瞬间而测得。

图2 Δt2略大于Δt1时产生的时间偏差

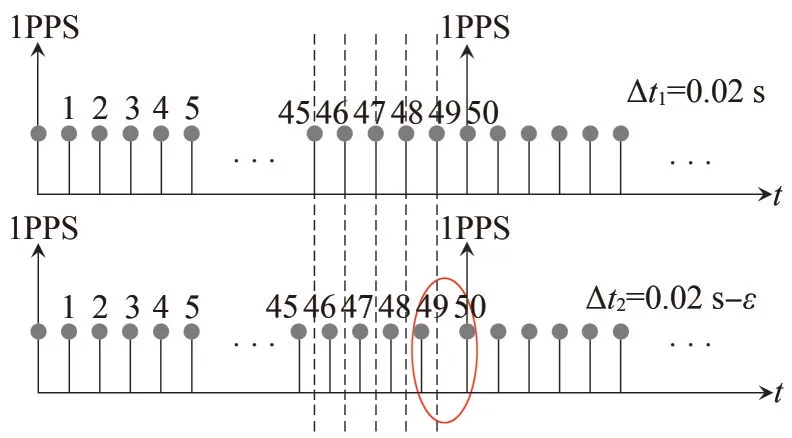
图3 Δt2略小于Δt1时产生的时间偏差

用电压相角的变化可以判断BDS 时钟是否精确，电压相角变化为

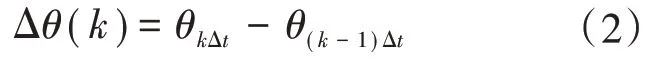
式中：k为采样数；Δt为采样间隔。

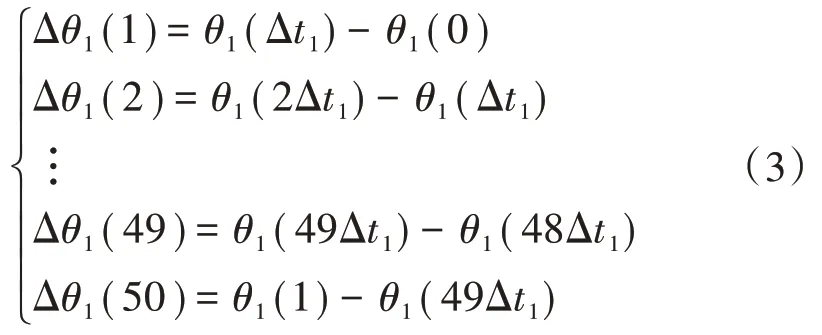
用Δθ1表示精确时钟下当采样率为50 次/s 时，电压相角在1 s 内的变化量。对于精确时钟，即Δt=50 s，每次采样后的电压相角变化为用Δθ2表示偏差时钟下当采样率为50 次/s 时，电压相角在1 s 内变化量。对于偏差时钟，即Δt2=0.02 s±ε，每次采样的电压相角变化为

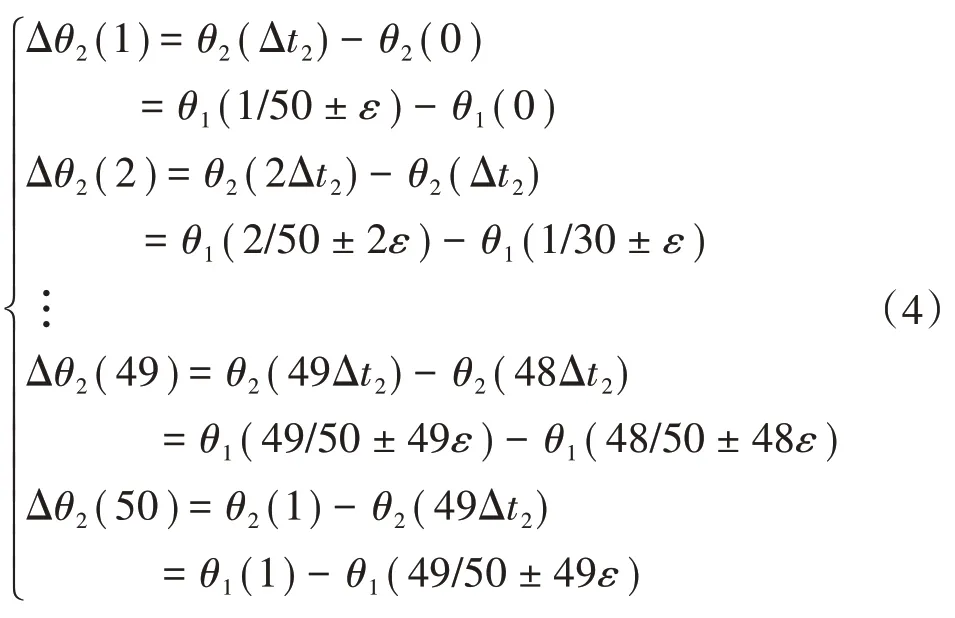
通过比较式（3）和式（4）中第50 次采样的电压相角变化可以看出，当时钟精确时，此时的时间间隔仍为0.02 s；当时钟存在偏差时，则时间间隔变为|0.02 s±ε|，从而导致电压相位发生偏移。精确时钟下和偏差时钟下电压的相位偏差实际测量结果分别如图4和图5所示。

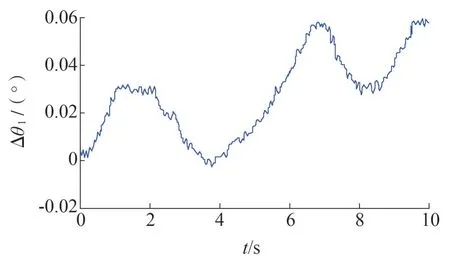
图4 精确时钟下电压的相位偏差

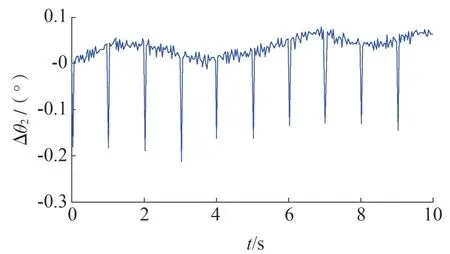
图5 偏差时钟下电压的相位偏差

由图4、图5 可知，当时钟精确时所测电压相角的变化很小，其绝对值在［0°，0.06°］范围内变化；而当时钟存在偏差时，电压相角差在每秒内都存在尖峰值，相角的最大误差能达到0.2°。

综上所述，BDS 时钟的授时精度对相角量测影响很大，下面分别从稳态系统和动态系统两方面详细研究BDS授时精度对相量量测的影响。

3 稳态下BDS偏差对μPMU量测的影响

3.1 系统频率为额定频率

当系统处于稳定运行状态，且工作频率为额定频率时，其电力信号的表达式为

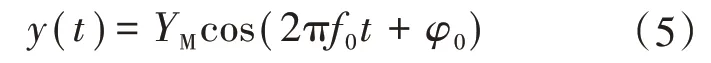
式中：YM为信号的幅值；f0为系统的额定频率；φ0为信号的初始相位。

电力输入信号的复指数表示形式为

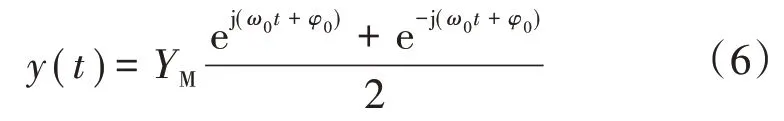
式中：φ0为额定角频率。

对信号进行采样，其中采样频率fs=Nf0，N为正整数，采样间隔ΔT=1/fs，则采样信号为

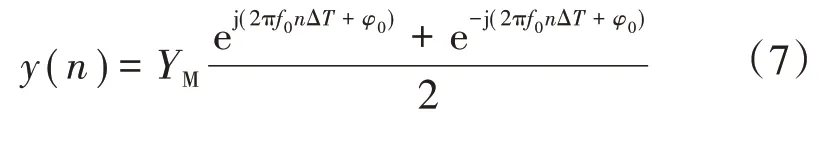
式中：n为采样数。

为了防止频谱泄漏，对系统信号进行汉宁加窗处理［16］，处理后的信号为

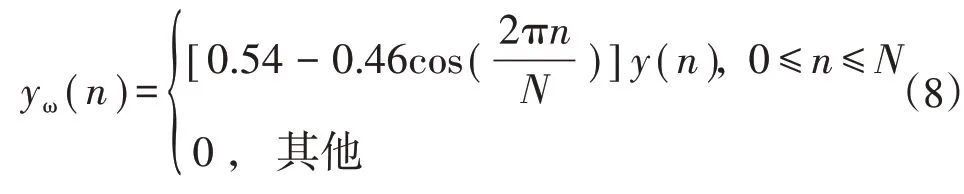
加窗后采样信号的离散傅里叶变换（Discrete Fourier Transform，DFT）表达式为

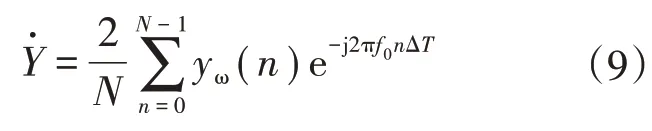
由于汉宁窗与正整数N和采样数n有关，与时间无关，可以将汉宁窗看作为K，则式（9）为

当BDS 的授时偏差为Δt时，即采样时刻发生了Δt的偏差，第n次采样得到的相量为

比较式（10）和式（11）可见，当系统在额定频率下稳态运行时，授时偏差Δt对相量幅值不会产生影响，对相角产生了2πf0Δt的偏差。

3.2 系统频率为非额定频率

当系统处于稳定运行状态，但频率为非额定频率时，此时的电力信号可表示为

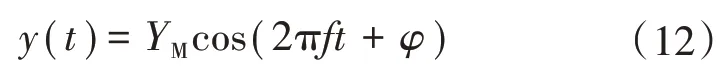
式中：f和φ分别为信号的频率和相位，经采样频率为fs的模数变换后得到采样序列y(n)为：

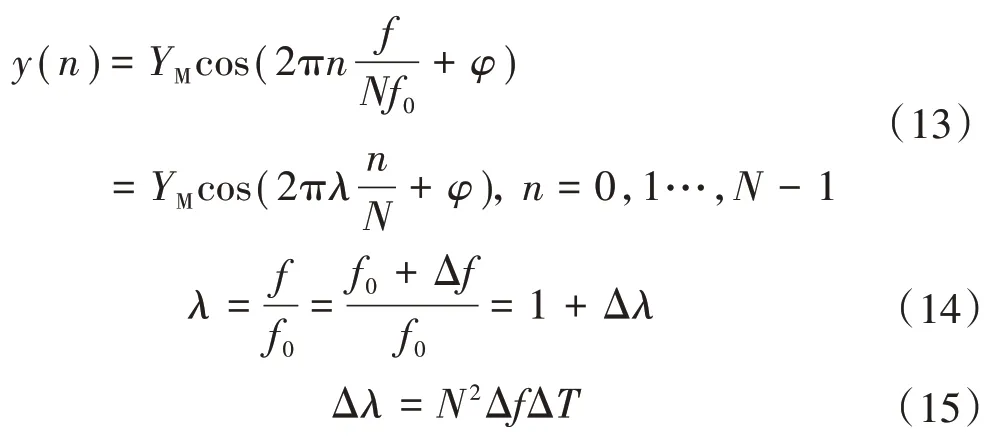
式中：ΔT为采样间隔。如果BDS 的1PPS 因干扰产生Δt的偏差，令T′=(ΔT+Δt)，此时的采样序列的实测值为

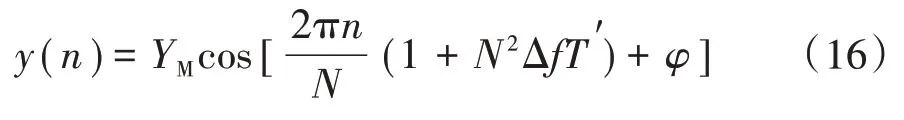
3.2.1 对同步采样的影响

同步采样即采样频率随系统频率的变化而不断调整，确保采样频率始终是系统频率的整数倍，即fs=Nf［17］。

式（15）中当Δλ=0 时即为同步采样，式（13）的DFT基波分量展开式为

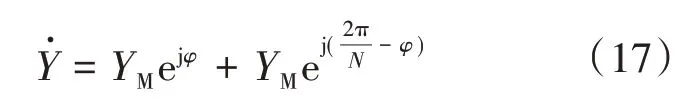
任意时刻t的向量为y(t)=

由式（17）可以看出，此时BDS 的授时偏差对相量的幅值和相角都没有影响。

3.2.2 对异步采样的影响

异步采样即采样频率为定值，不随电力信号基波频率的变化而调整，此时Δλ≠0［18-19］，式（6）的DFT基波分量展开式为

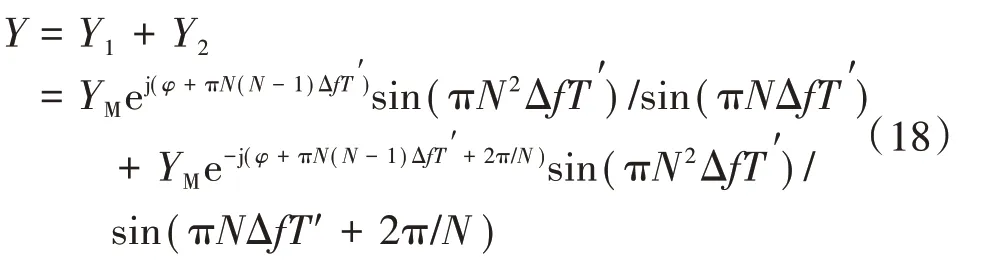
式中：Y1和Y2分别为采样信号的两个分量。

授时偏差Δt对相角测量结果的影响如图6所示。

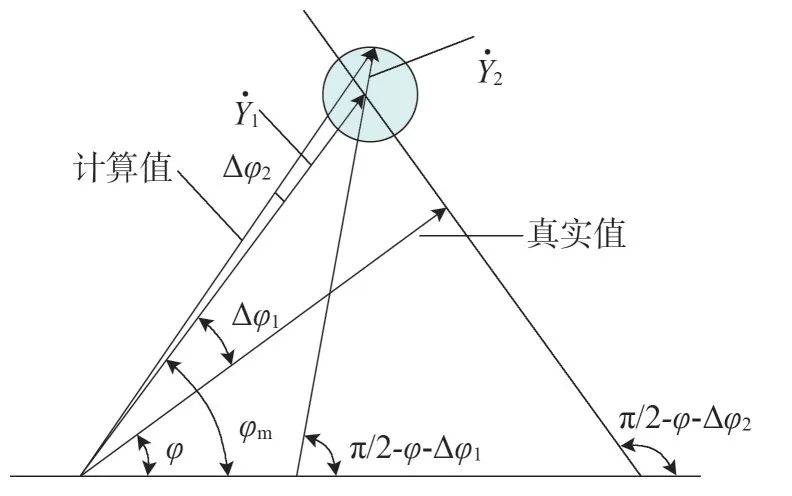
图6 时间偏差对相角测量结果的影响

图6中，Δφ1=N(N-1)πΔfT′，φM为测量相量的相位，相角测量误差为

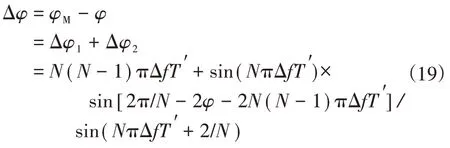
式中：Δφ1和Δφ2分别为信号两个分量Y1和Y2分别产生的相角差。

由以上分析可知，BDS 的授时偏差Δt对相量幅值不会产生影响，但对相角偏差影响很大。

当系统在非额定频率下稳态运行时，同步采样时BDS 的授时偏差对相量幅值和相位的量测没有影响，异步采样时BDS 的授时偏差对相量幅值虽不会产生影响，但对相位会产生一定的测量误差。

4 动态下BDS偏差对μPMU量测的影响

电力系统在动态条件下电压、电流信号不再是纯正弦信号，动态条件下的电力信号模型为

式中：YM(t)为动态条件下信号的幅值；f(t)为动态条件下信号的频率；Δf(t)为动态条件下频率的偏差。

为了防止频谱泄漏，将传统的DFT 算法与数字低通滤波器相结合，得到消除高频分量后的相量为

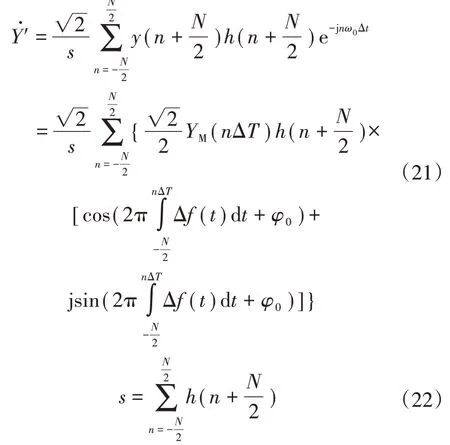
在系统振荡期间，幅值、相角、频率等量的变化是非线性的，且为时间相关的函数，为了在采样窗内近似描述这种动态变化，可以用二阶泰勒级数展开式模拟相量各参数的波形变化，即为

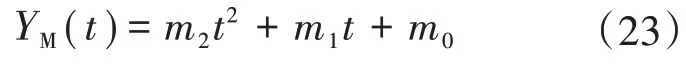
式中：m2为二阶导数；m1为一阶导数；m0为常数。

将式（23）代入式（21）得

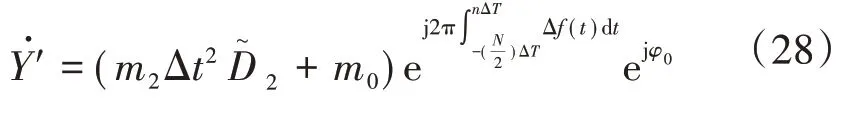
由于时间标记设置在数据窗的中间，所以该点的实际相量为

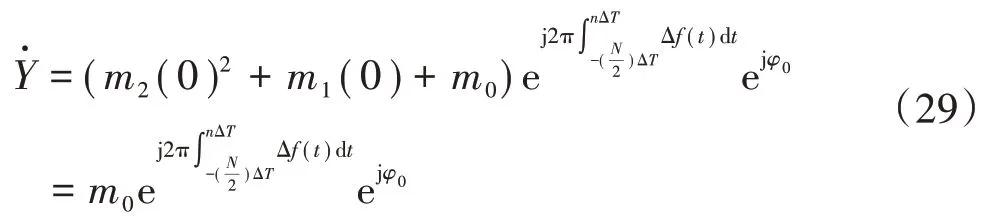
因此，相量测量误差为

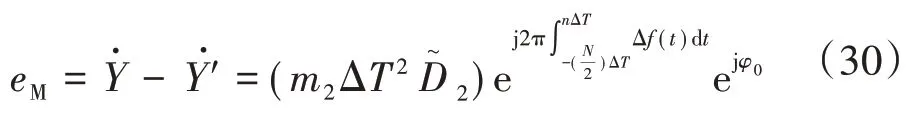
当授时偏差为Δt时，则采样间隔变为KΔT+Δt，相量测量误差为

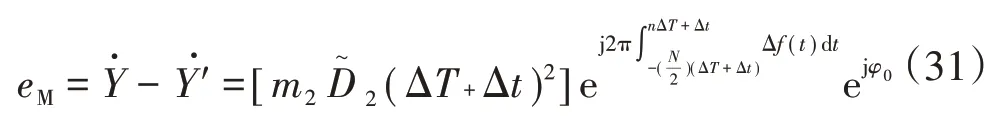
幅值偏差为

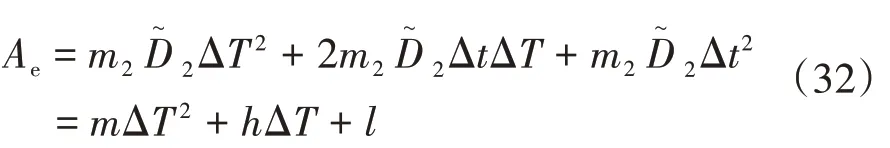
式中：m、h、l为常量。

由于动态情况下，频率是动态变化的，假设频率偏差Δf(t)=2t，则相位偏差为

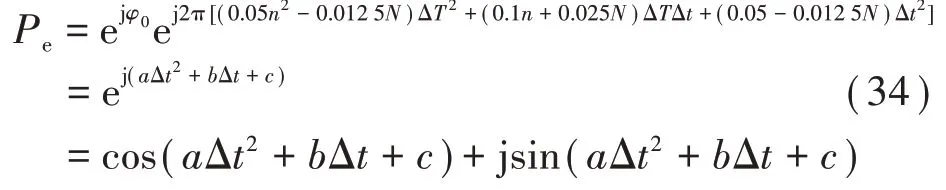
由于实际运算中，样本数N、滤波器系数h(n+)、加权平均值及采样间隔ΔT都为定值，所以式（34）中a、b、c也为定值。由式（32）和式（34）可见，当Δt为定值时，幅值误差和相位误差都为定值；当Δt变化时，幅值误差的变化轨迹为抛物线，相位误差的变化规律近似为正弦曲线。

5 仿真分析

为验证上述理论，利用MATLAB 分别进行稳态和动态仿真分析。考虑到BDS 授时精度会受环境、电磁干扰等因素影响，为了能直观反映授时偏差Δt对相量测量精度影响，试验中Δt取值为

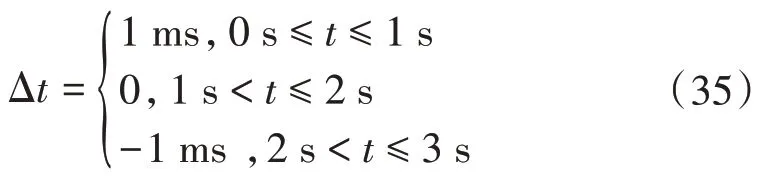
稳态下的测试信号为

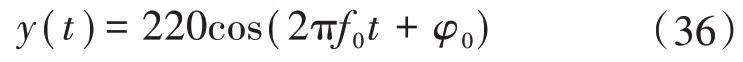
式中：f0=50 Hz，φ0=π/3，测试信号的时长为3 s。图7、图8 分别为系统稳态情况下无授时偏差和授时偏差为Δt时电压幅值、相位的仿真结果。

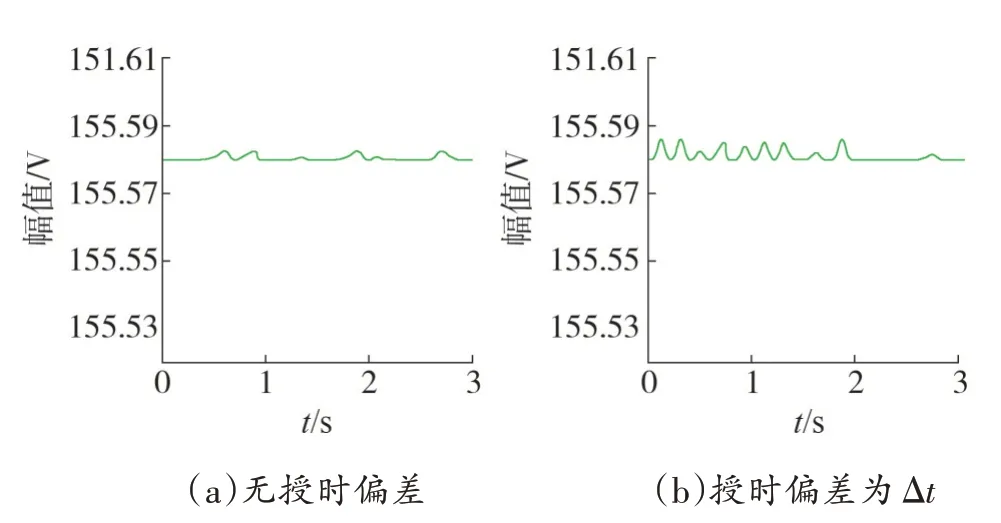
图7 稳态时的电压幅值

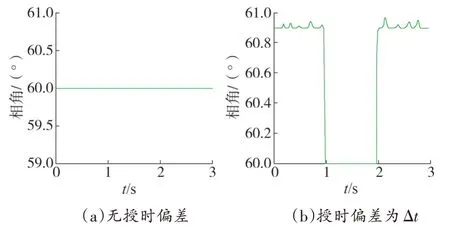
图8 稳态时的电压相位

由图7、图8 可知，授时偏差为±1 ms 时，相角偏差约为0.9°，满足2πf0Δt的理论偏差；电压幅值偏差约为0.01 V，授时偏差对幅值的影响可忽略。

动态情况下的测试信号如式（32）所示，YM(t)=220 V，f0=50 Hz，φ0=π/3，为了简化计算，设频率偏差Δf(t)=2t，m=h=l=0.5，样本数N=200，测试信号的时长取20 s。无授时偏差和授时偏差为Δt时的电压幅值、相位的实验结果如图9和图10所示。

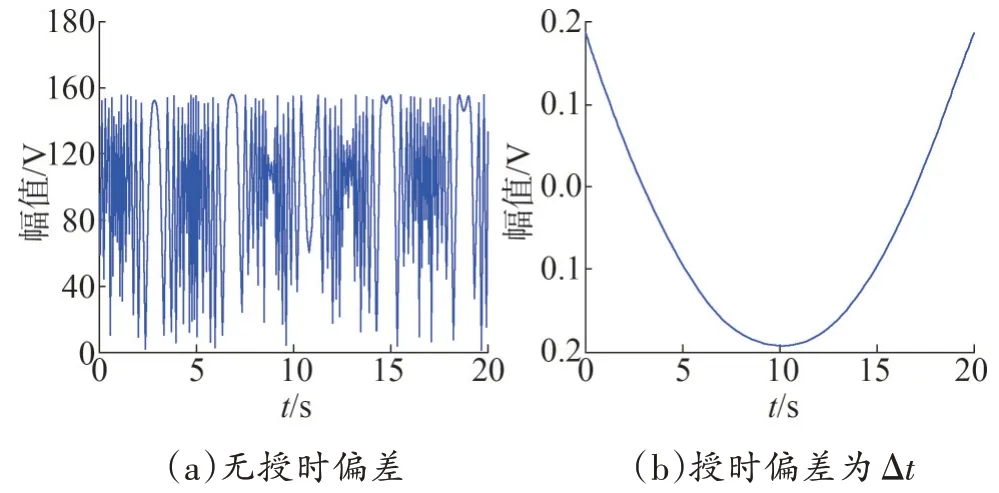
图9 动态时的电压幅值

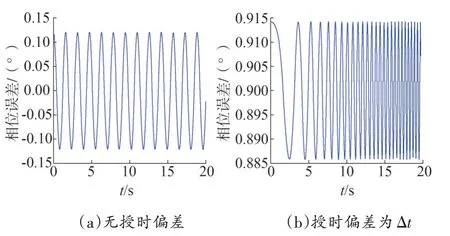
图10 动态时电压相位偏差

由图9、图10 可见，动态情况下，授时偏差为±1 ms 时，电压幅值随时间不停变化，由于受频率偏差Δf(t)=2t的影响，电压幅值不再满足简单的正弦规律。授时偏差Δt与无授时偏差的电压幅值差小于0.2 V，满足抛物线的理论分析。授时偏差Δt下的相位误差约为0.9°，且随时间的增加，偏差波动越明显，符合相位偏差近似正弦曲线变化的理论分析结果。

为了更直观地描述授时偏差大小对相量测量误差的影响，对授时偏差分别为1 μs 和1 ms 的TVE 值进行比较，如图11所示。

由图11 可知，授时偏差与相量总误差（Total Vector Error，TVE）值成正比。当授时偏差为1 μs时，能够满足标准中TVE 值小于1%的要求［20-21］。由于BDS 的授时偏差能达到纳秒级别，因此，基于BDS的配电网μPMU 的相量测量精度会更高，尤其是相角测量将会更精确。

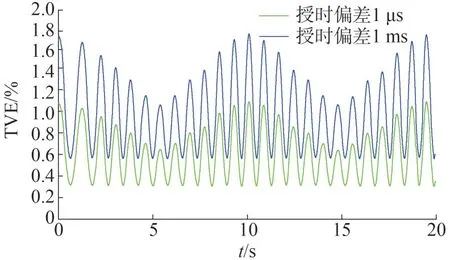
图11 授时偏差分别为1 μs和1 ms的TVE值

6 结语

在研制的配电网μPMU 与故障录波装置的基础上，着重研究了当装置时钟源更换为BDS后对相量幅值、相位可能带来的影响。从稳态和动态两方面推导了授时偏差对相量幅值、相位的误差影响表达式，并通过MATLAB仿真验证了理论分析结果。稳态时，BDS授时偏差对相量幅值没有影响，对相位将会差生一定的偏差；动态时，BDS 授时偏差对相量幅值偏差的影响按抛物线规律变化，对相位偏差的影响近似正弦曲线，且随时间的增加，误差波动会越明显。综合以上分析，结合BDS 授时偏差为纳秒级的因素，基于BDS的μPMU相量测量精度比之前的装置将有所提高。

研究结果将为配电网μPMU 与故障录波装置的改进，配电网相量测量精度的提高提供良好的基础。