VMD和小波阈值重构的电力电缆局部放电信号去噪法

赵永梅

(国能技术经济研究院有限责任公司,北京 102209)

0 引 言

矿用电力电缆的绝缘性能直接关系着煤矿供电系统的安全可靠性，测量局部放电信号能够提前判断电力电缆的绝缘性能。然而局放信号本身较弱，其幅值与现场其他电磁波等干扰信号相差较小，故局放的检测过程中受到的干扰严重，导致采集信号的信噪比低。因此，尽可能地保证局放信号不失真，同时增加采集信号的信噪比是电力电缆进行局放检测的关键。

局放信号具有非线性、时间序列非平衡的特征，且频带范围分布较广，所以很难通过选取局放信号的频带进行有效去噪[1]。目前，局部放电的去噪方法主要有经验模态分解法(empirical mode decomposition，EMD)和小波阈值法。EMD方法递归地检测信号中的局部最大值和最小值，高度依赖于极值点搜索法，根据能量法则直接丢弃了阶数小的本征模态(intrinsic mode function，IMF)，使得部分有用信号丢失[2-6]。小波变换可以实现信号在时域和频域上同时局部化，具有良好的时频分析能力[7-9]，但小波变化会导致局放的暂态过程丢失。

2014年Konstantin Dragomiretskiy基于EMD最早提出了变分模态分解法(variational mode decomposition，VMD)[10]。相较于EMD，VMD的分解层数少，具备严密的数学理论，提高了对噪声干扰的鲁棒性[11-19]。VMD法能够较为完整的保留局放的暂态过程，但对噪声的抑制能力较弱。综上所述，对于受现场干扰信号影响较为严重的局放信号，上述方法在单独使用时的滤波效果均不太理想。

笔者提出的基于VMD和小波阈值的电力电缆局部放电信号去噪方法，结合了VMD法能够自适应地调整各模态中心频率和小波阈值良好的时频分析能力的优点，同时避免了VMD法对噪声抑制能力较弱和小波阈值丢失暂态过程的缺点，用于提高局放信号的信噪比，更好地保留局放信号的有效信息。对比分析和实验表明，该方法的去噪效果优于现有其他方法。

1 基本原理

1.1 VMD算法

VMD能够自适应、非递归地将输入信号分解为多个具有特定稀疏性质的IMF，且每个IMF均有对应的中心频率。分解过程中不断地评估各个模态，使各IMF及其中心频率的分布达到最优。VMD法的主要分解过程如下。

1)初始化确定IMFs的个数K，对于每个本征模态uk，k=1，2，…，K，通过希尔伯特变换计算相关的解析信号，从而获得单边频谱。

(1)

2)将每个本征模态uk乘以e-ωkt，使其与对应的预测中心频率ωk进行频率混合，从而将子信号的频谱移位到“基带”。

(2)

3)通过解调信号的高斯平滑度来估计带宽。产生的约束变分问题见式(3)。

(3)

式中 {uk}为所有本征模态集合；{ωk}本征模态对应的中心频率集合。

4)通过二次惩罚项α获得了良好的收敛性，同时通过拉格朗日乘子λ(t)严格地重建约束。引入的增广拉格朗日见式(4)。

L({uk}{ωk},λ)=

(4)

5)步骤(3)中最小化问题的解可用AMMD[20]求得。通过交替更新来求最小值点，本征模态uk的交替更新表达式见式(5)。

(5)

式中ωk和ui≠k为最近可用的更新值。将上述问题转换到在频域求解，求解结果见式(6)。

(6)

将公式(6)中的第1项中的变量ω←ω-ωk进行变更，并转化为非负频率上的积分形式。

(7)

最后，得到二次优化问题的解见式(8)。

(8)

按照与uk同样的求解过程，中心频率ωk的二次优化问题的解见式(9)。

(9)

得到的新的ωk是相应的本征模态uk的功率谱的中心。

1.2 小波阈值算法

小波阈值法的基本原理是，含噪信号经小波分解后，可得到原始信号和噪声的分解系数，且原始信号的分解系数大于噪声的分解系数，因此，需选取合理的阈值，当分解系数大于阈值时认为分解系数由原始信号而来，保留相应的信号分量；反之，当分解系数小于阈值时，舍弃相应的信号分量[7]。

小波阈值算法的关键是确定小波基、分解尺度以及阈值函数。经分析，选db.4小波作为小波基，分解尺度为3层，阈值的计算采用固定阈值估计法。为了保证信号的平滑性，选用软阈值函数进行处理。软阈值函数的数学表达式见式(10)。

(10)

2 基于VMD和小波变换的局放信号去燥

局放信号的频带宽，主频率不明显[21-25]。通过上述基本原理可知，VMD法可以自适应地将局放信号分解为多个具有中心频率的本征模态。为了既能将局放信号从干扰中提取出来，又能尽可能地保留局放信号暂态过程。根据VMD与小波阈值的基本原理，笔者提出一种基于VMD与小波阈值重构的局放去噪方法。首先，利用VMD法将实际输入的信号分解为K个初始信号{u1,u2,…,uK}及其对应的初始中心频率{ω1,ω2,…,ωK}，利用公式(6)～(9)，不断更新uK，直至各uK的精度小于其判别精度，停止更新分解出K个IMFs，即{u1,u2,…,uK}及其对应的中心频率{ω1,ω2,…,ωK}；然后，对每个IMF进行小波阈值去噪，进一步将每个IMF去噪处理，从而得到每个IMF的去噪分量，最后对所有IMFs的去噪分量进行信号重构，得到去噪后信号。

VMD分解过程中，IMFs的个数K和惩罚因子α是决定信号分解效果的主要因素。其中，K值太大会造成各IMFs的中心频率发生重叠，太小会导致信号中某一频带的分量同时出现在多个IMFs中。因此，须通过多次尝试来确定K的取值。

2.1 本征模态个数K

经多次反复试验发现，当K=5时，信号的分解效果最好，此时本征模态分量及其对应的频谱如图2所示。可以看出，模态u2的频谱峰值与含噪信号的频谱峰值重合，模态u3的频谱峰值与含噪信号在2 MHz附近的峰值重合，此时含噪信号的VMD分解效果最好。

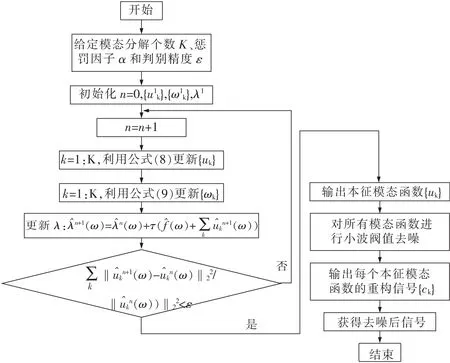
图1 VMD与小波阈值去噪重构流程

图2 K=5时本征模态分量波形及频谱

2.2 惩罚因子α

确定K值后，对惩罚因子的取值做大量的测试。通过重构信号与原始“纯净”信号的相关系数来确定惩罚因子，图3为惩罚因子在200～5 000之间变化时对应的相关系数的走势图。可以看出，当α取值在600～2 800范围内时，相关系数大于0.64，即信号的重构效果最佳，因此α的取值在该范围内均可，取值α=1 000。

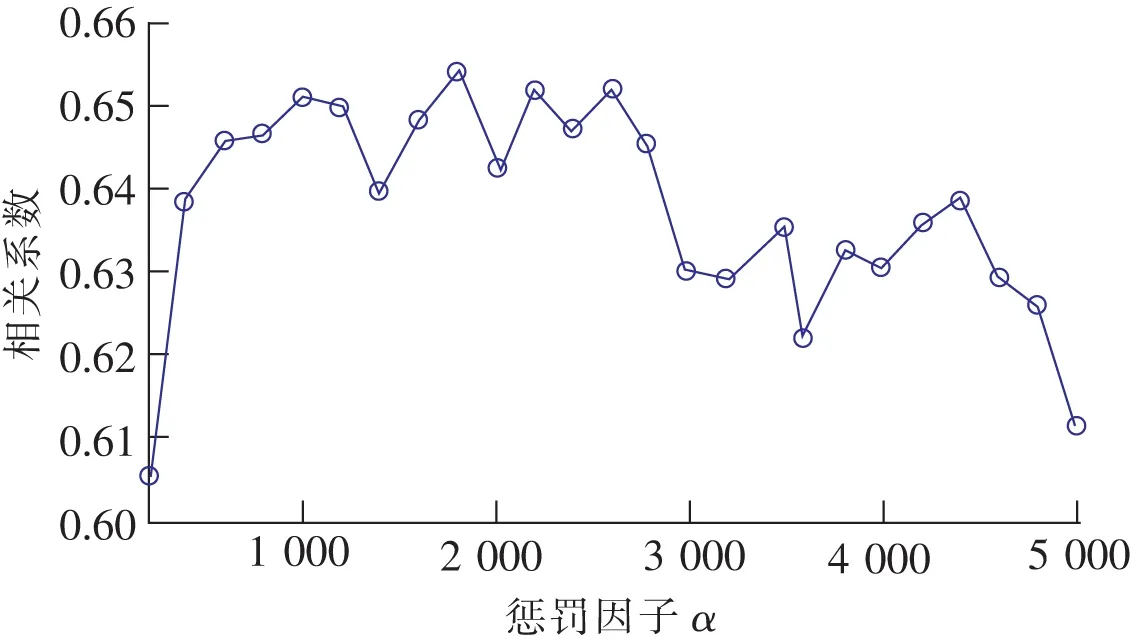
图3 不同惩罚因子对应的信号相关系数

确定α值后，对含噪信号进行VMD分解，分解后得到的各模态分量uk中仍含有明显的噪声干扰，因此分别对各模态分量uk进行小波阈值去噪，以达到更好的去噪效果。如图4(a)为各本征模态uk的波形，图4(b)为各本征模态经小波阈值处理后得到的对应波形ck。

从图4可以看出，各本征模态分量uk经小波分解后得到的重构信号ck中，噪声被明显抑制。特别是，在u4和u5中局放分量被完全淹没在了噪声中，经小波阈值分解后，c4和c5中局放分量明显。VMD的特点是可以将一个宽频带信号分解为由多个窄频带组成的信号，因此有学者通过VMD对IMFs进行选择性的取舍，实现了低频混合信号或低频含噪信号的分离。但是局放脉冲信号的特征在于其频带极宽且难以找到固定的主频率，因此对IMFs的舍弃会导致有用信号的信息缺失。通过小波阈值去噪的二次处理，有效地去除了噪声干扰，极大限度地保留了各IMFs中的有用信号。

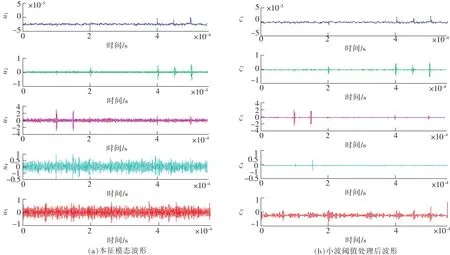
图4 本征模态分量及其小波阈值去噪信号

3 与EMD自相关、小波变换对比分析

将经小波阈值处理后的信号ck进行重构，得到基于VMD和小波阈值的重构信号。为了对比笔者提出的局放去噪方法的去噪能力，将该方法与目前几个主流的局放去噪方法进行比较。图5为含噪的局放信号经VMD、小波阈值、EMD自相关以及VMD和小波阈值重构等方法处理后的重构信号波形。其中，EMD自相关法是经EMD法改进后的去噪方法，其去噪效果优于EMD法。可以看出，笔者提出的基于VMD和小波阈值重构法优于其他3种方法，并且很好的保留了局放信号的暂态部分。经小波阈值处理后的信号的去噪效果也比较显著，但是局放信号的暂态部分缺失较为严重。

从图5可以直观地看出,各种方法的去噪能力，为了进行进一步的定量比较，结合实际情况，对不同信噪比的局放信号进行去噪，同时引入信噪比SNR、相关系数R以及均方根误差RMSE作为判断去噪能力的依据。

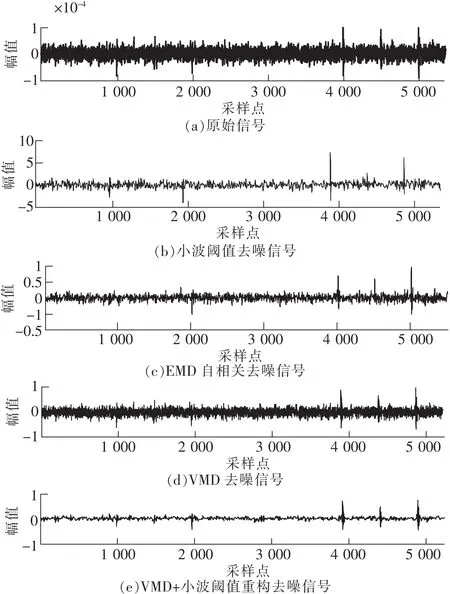
图5 3种方法的去噪效果对比(原信噪比-2.673 dB)

可以看出，VMD与小波阈值重构法的去噪效果明显优于VMD法、EMD自相关法和db4小波阈值法，尤其是对于信噪比愈小的信号，其去噪效果愈加显著,见表1。

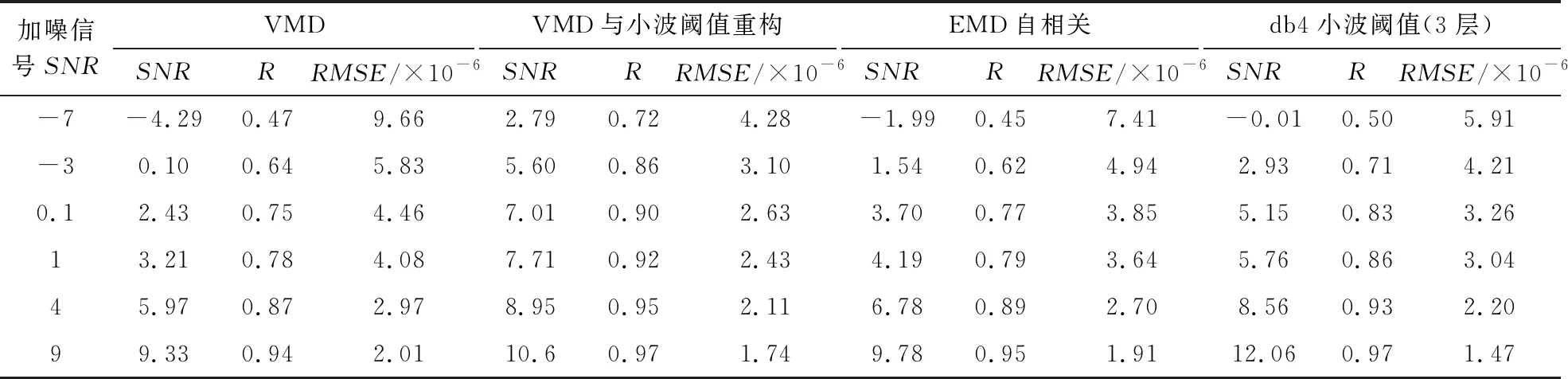
表1 4种方法抑制噪声效果比较

4 实验信号分析

为了进一步验证文中提出的去噪方法对实测信号的去噪效果，在实验室中对6 kV电力电缆施加2.5 kV直流电压，采用检测阻抗法测量其局放电压信号，并通过Matlab处理实验获得的信号数据。图6(a)为实验室实测到的局放信号的波形，可以看出局放信号几乎淹没在噪声干扰中。图6(b)和(c)分别是利用VMD法和VMD与小波阈值重构法对实验信号进行去噪处理后的信号。

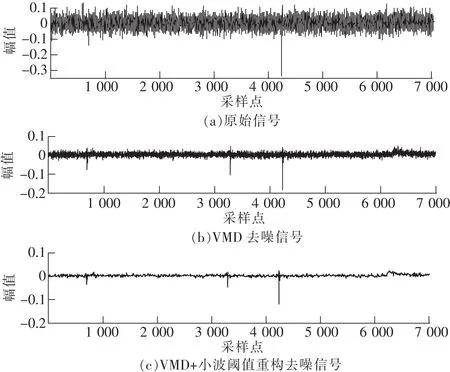
图6 实验局放信号分析

从图6可以看出，变分模态分解法去噪后，信号中仍然存在震荡现象和较多的噪声含量。经VMD与小波阈值重构的去噪信号中不存在震荡现象，同时噪声被明显地抑制。由于信噪比 、相关系数以及均方误差的计算需要原始“纯净”信号，而实验信号的原始“纯净”信号未知，故此处引入信号去噪前后的噪声抑制比(noise rejection ratio，NRR)来衡量去噪效果。NRR表征去噪后有效信号的突出程度。表2所示为2种方法的NRR计算结果。

(11)

可以看出，VMD与小波阈值重构法的噪声抑制能力更优越，优于VMD法。

5 结 论

矿用电力电缆早期绝缘劣化时产生的局部放电特征信号微弱，受现场环境干扰较为严重，故障识别准确率低。为了提高局放信号的信噪比和故障识别准确率，提出一种基于变分模态分解和小波阈值重构法。

经仿真和实验分析表明，根据所处理的信号，须提前确定VMD法的分解个数与惩罚因子，以确保其去噪能力。VMD方法能够自适应地将信号分解为多个频带的模态，且各模态及其中心频率在不断地更新，同时恰当地平衡各模态之间的误差，使各模态的分布达到最优。通过小波阈值法对各模态分量作进一步处理，可以提高各模态的信噪比。与现有的去噪方法比较，对于信噪比越低的局放信号，VMD与小波阈值重构法的滤波性能越好。目前需通过多次尝试确定K值，后续将研究自动求解最优K值的方法。