基于动态贝叶斯网络的电源系统可靠性分析与故障诊断

2021-08-04黄洪钟李彦锋

电子科技大学学报 2021年4期

李享，黄洪钟，黄鹏，李彦锋

(电子科技大学系统可靠性与安全性研究中心成都 611731)

电源系统是由配电设备、储能设备、调波设备、开关设备、充电控制设备以及相关电线电路组成的总体[1]，为各种电机提供高/低频、交/直流电源，其可靠性直接影响整个电机系统的平稳运行[2]。然而，电源系统结构复杂、设备繁多，如何理清其系统结构，识别主要脆弱点和关键薄弱点，影响并制约着供电任务的平稳实施。传统的静态可靠性分析方法只能应用于固定时刻的系统可靠性分析，在所有电源设备集成为一个动态系统时，其复杂结构、高危高压、动态失效的运行特点，使得该系统可靠性问题需采用动态的分析方式。

动态系统可靠性分析方法是近年的研究热点及难点，DBN从这些方法中脱颖而出。机器学习[3]、数据挖掘[4]等技术的兴起也为DBN的发展和应用提供了更为广阔的空间。目前，DBN的理论成果得到了进一步的发展完善，包括因果推断[5]、不确定性知识表达[6]、模式识别[7]和聚类分析[8]等。DBN也因其在双向推理及故障诊断方面的优势，被广泛应用于复杂系统的动态可靠性分析。文献[9]通过引入 β因子，结合模糊DBN，提出了一种针对数据缺失的多态系统可靠性分析方法。文献[10]基于贝叶斯网络对海上浮式风机进行了可靠性分析，大幅提升了故障诊断的准确率。文献[11]利用隐马尔科夫模型度量证据节点的先验概率，结合DBN，实现了化工设备的任务可靠性预计与评估。

现有的DBN算法主要分为：离散时间贝叶斯网络算法(discrete-time Bayesian network, DTBN)[12]与连续时间贝叶斯网络算法(continues-time Bayesian network, CTBN)[13]。其中，DTBN以离散任务时间的方式，通过定义节点的条件概率表(conditional probability table, CPT)及边缘概率表(marginal probability table, MPT)，求解出系统在不同任务时间片的后验概率。其中，文献[14]基于DTBN与改进的GO-FLOW方法，研究分析了多阶段多状态系统的共因失效问题。文献[15]通过引入区间分析理论，对无人机中表决系统的不确定性问题进行了量化处理，并基于DTBN算法对该系统进行了可靠性建模分析。然而，随着系统节点数与时间片数的增加，CPT&MPT的维度呈指数增加[16]，导致求取系统可靠度所需的计算量也指数增长。

CTBN可在连续任务时间条件下，建立各个节点的概率密度函数(probability density function,PDF)的解析解，并借此得出任意时刻节点的后验概率，极大地减少了计算时间。文献[17]基于CTBN构建车辆系统的性能函数，并将其应用于该系统的可靠性优化设计。文献[18]通过模糊函数量化了失效数据的参数不确定性，并针对DBN中的动态逻辑门，构建了基于CTBN算法的模糊函数解析解模型。然而，现有的CTBN算法，需要针对不同的分析对象建立特定的分析模型，缺少通用的建模方法[19]。

因此，本文提出一种改进的DBN概率表建模方法，在无需离散任务时间的情况下，实现电源系统的动态可靠性分析与故障诊断。

1 动态贝叶斯网络

1.1 离散时间贝叶斯网络

在DTBN算法中，任务时间被离散为多个时间片段，且节点的条件概率与边缘概率以CPT和MPT的形式给出。以2时间片段的DTBN为例，“与”门的CPT&MPT如图1所示。对于节点A和B，P1和P2分别代表节点在对应时间片中的失效概率，而状态3的概率1 -P1-P2表示该节点在任务时间内未发生失效的概率。而在“与”门的CPT中，P(T=1|A=1,B=1)=1表示节点A和B在第一个时间片中失效时，该“与”门在此时间片内失效的条件概率为1，其他的概率也类似定义。基于图1的CPT，可通过式(1)～式(3)求解出节点T在各个状态的边缘概率。

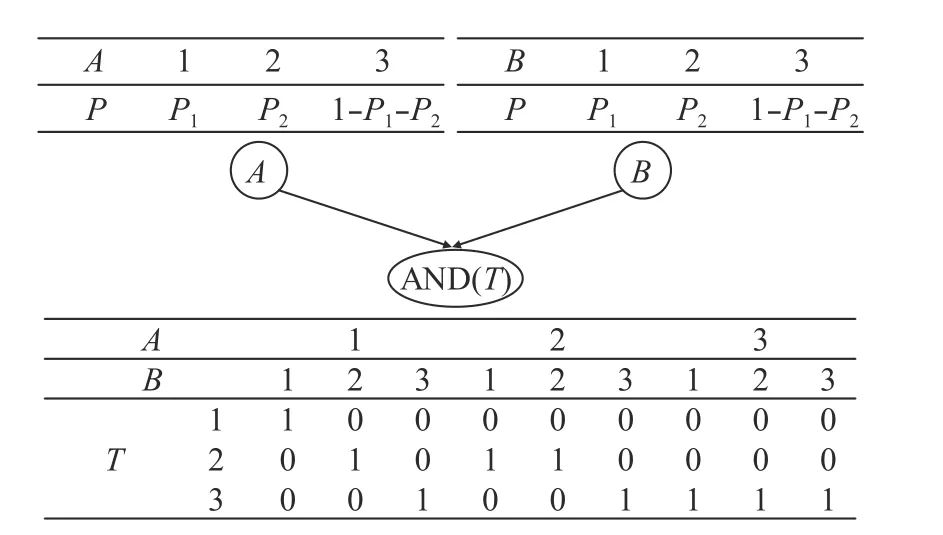
图1 CTBN中“与”门的CPT&MPT

1.2 连续时间贝叶斯网络

则求解出节点T的PDF为：

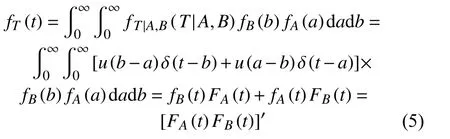
但是，正如引言中介绍的，现有的CTBN算法，需要针对不同的分析对象建立特定的解析解模型。并且随着动态逻辑门和节点数的增加，该方法的建模难度也会随之增加。因此，本文提出一种改进的CPT&MPT建模方法。

1.3 概率表建模

以“与”门的CPT&MPT为例，如图2所示，P(A=1)=FA(t)表示节点A在该时间点的失效概率，而P(A=2)=RA(t)=1-FA(t)表示节点A在该时间点的可靠度。通过图2中节点T的CPT，则可由式(6)得出该节点的边缘概率分布。

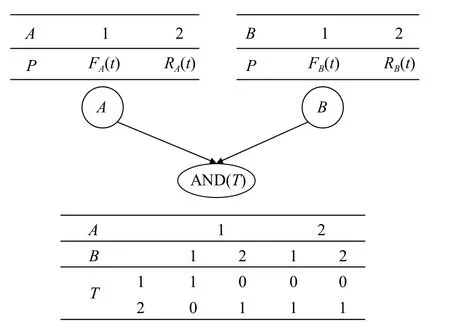
图2 “与”门的CPT&MPT

可以看出，该CPT与传统CTBN算法中的单位阶跃函数和脉冲函数有相同的功能。且通过算法1，可以计算出任意数量节点的“与”门CPT，且该“与”门的父节点可以服从任意的失效分布类型。

算法 1 由i个节点组成的“与”门的C PT 计算

而针对动态贝叶斯网络中的动态逻辑门，以温备份门为例(warm spare, WSP)，如图3所示，节点B为节点A的温备份节点。当节点A正常运行时，节点B处于温备份状态，其失效率 λB下降为αλB， α为备份因子，且 0 ≤α≤1。当 α=0时，节点B转变为冷备份节点； α =1时，节点B转变为热备份节点。当A失效时，B转变为工作状态，且失效率转变为 λB。则节点B的条件概率可由式(7)～式(10)得出。

图3 温备份门的CPT&MPT

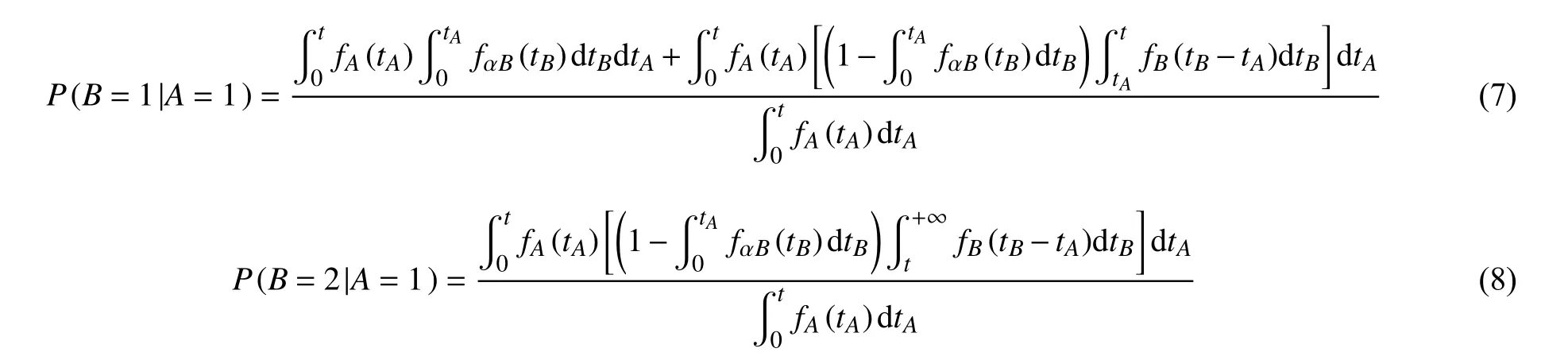
式中，fA(t)、fB(t)分别为节点A和B工作时失效概率的PDF；fαB(t)为节点B在温备份状态下的PDF；tA、tB分别为节点A和B的失效时间。针对电子系统，当节点A和B的失效类型服从指数分布时，即fA(t)=fB(t)=λe-λt，fαB(t)=αλe-αλt，则节点B的CPT如表1所示。

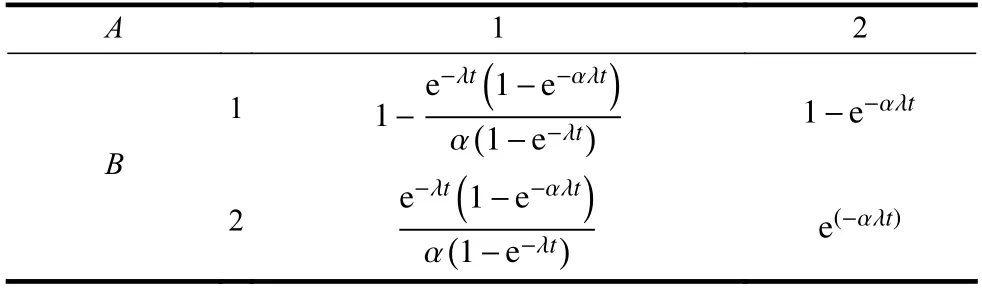
表1 温备份节点B的CPT

为验证所提方法的准确性，以图3中的温备份门(节点T)为例，将各节点的CPT&MPT代入算法2中，当 λA=λB=0.00001， α=0.5时，可计算出T节点的可靠度曲线，分别与蒙特卡罗仿真(Monte Carlo simulation, MCS)[18]以及DTBN的计算结果进行了对比，如图4所示。

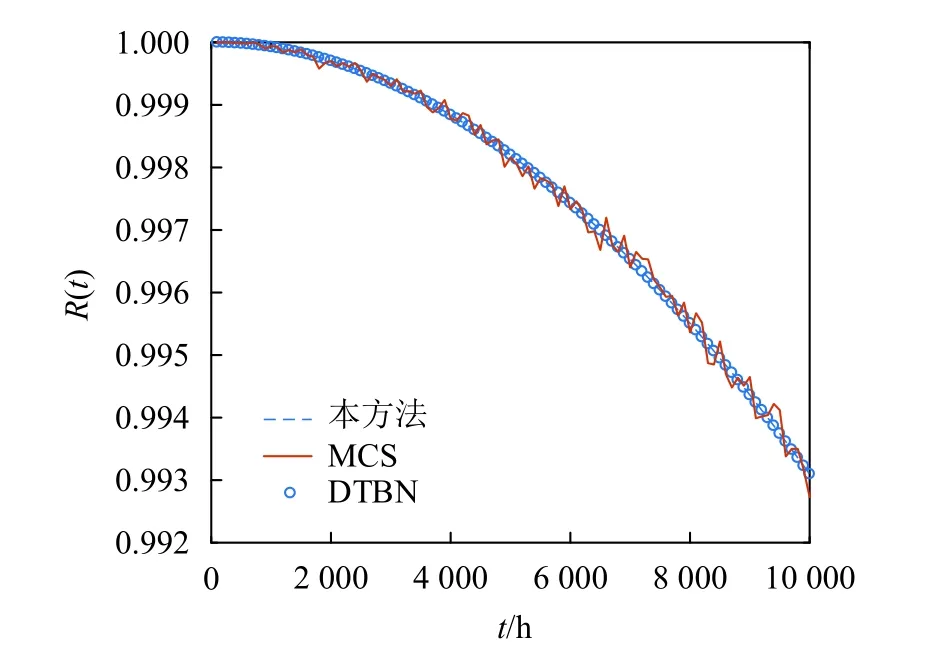
图4 结果对比分析

算法 2：DBN后验概率求解算法

由图4结果可知，所提方法可在未离散任务时间的情况下，获取与DTBN相同的系统可靠度计算结果。而且，本方法B节点的CPT维度仅为(2×2)，即便是与最简单的2时间片段DTBN相比，其建模难度也远小于DTBN的CPT[16]。与MCS的计算结果的对比分析结果也验证了所提方法的准确性。

由表1的CPT可求解出B节点FB(t)的解析解，如式(11)所示，其结果与CTBN[19]一致。并且，通过将构建的CPT&MPT与算法2相结合，即可计算得到观测节点的后验概率，而无需针对不同分析对象建立特定的解析解模型。

2 电源系统的动态贝叶斯网络建立

本文以某电源系统为研究对象，该系统组成结构如图5所示。

图5 电源系统结构框图

该系统通过将民用电转换成高压直流电，给规定容量的主预储能电容器充电。在规定的时间范围内达到指定值，在规定的时序触发下，主、预储能电容通过晶闸管固态开关、平波电感给负载放电，为负载提供合适的能量脉冲，使它们的形状、幅度和时序保持一致。根据该电源系统的结构框图，可建立其DBN如图6所示，事件编号及失效率如表2所示。

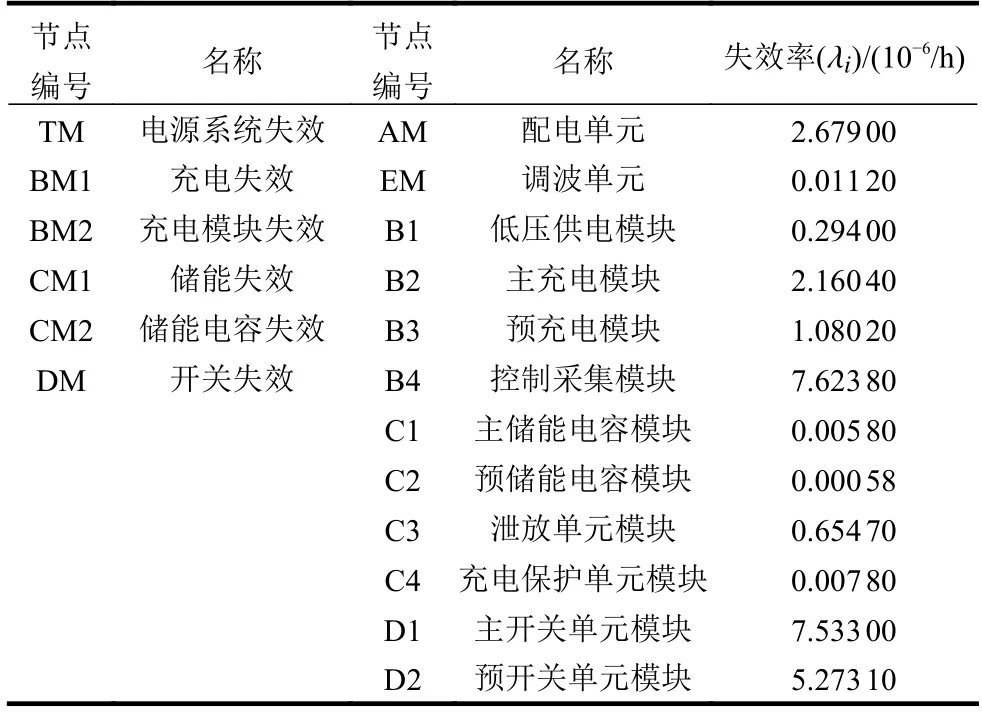
表2 事件节点编号及失效率

图6 电源系统的DBN

3 电源系统的可靠性分析与故障诊断

该电源系统的DBN模型中，包括3个WPS门(BM2、CM2、DM)，其组成节点的CPT&MPT如图3所示，节点B3、C2、D2的CPT可由表1计算。将各节点的CPT&MPT代入算法2中，即可求解出各个节点的后验概率。各节点状态为2时的边缘概率即为该节点对应事件的可靠度值。通过算法2，可以求解出电源系统顶事件及中间事件在任务时间内(5×105h)的可靠度变化曲线，如图7所示。其中，节点AM为底事件节点，且服从指数分布，所以其可靠度曲线是典型的指数分布曲线。根据表2中的失效率数据，因为与节点EM、CM1、CM2相关联底事件的失效率太低，所以在任务时间内上述3个节点的可靠度没有明显变化。其他的节点(TM、BM1、BM2、DM)则由各种逻辑门组合而成，因可靠度不服从特定分布，所以曲线呈现出图7所示的变化趋势。

图7 电源系统可靠度曲线

基于算法2，可以求解出顶事件TM状态为1时，其他节点i状态为1的后验概率P(i=1|TM=1)(i=AM、BM1、BM2、CM1、CM2、DM、EM)。即电源系统失效时，其他节点失效的条件概率，该条件概率可用作系统失效下部件故障的诊断分析。诊断结果如图8所示，在0.875×105h前，节点AM的后验失效概率最大，此时段若系统失效，则配电单元失效的概率最大。而在(0.875～2.9)×105h之间，则是DM节点(开关失效)的后验失效概率最大。在1.925×105h时刻，BM2(充电模块失效)的后验失效概率超过AM节点，且在2.9×105h之后成为后验失效概率最大的节点。