航天器姿态跟踪有限时间自适应积分滑模控制

冯昱澍，刘 昆，冯 健

(1. 国防科技大学空天科学学院 长沙 410073；2. 北京跟踪与通信技术研究所 北京 海淀区 100094；3. 中山大学航空航天学院 广州 510006；4. 中国人民解放军96901部队 北京 海淀区 100094)

航天器要完成空间探测、开发空间等特定的飞行任务，对姿态控制提出了各种要求。其中对地观测卫星在轨运行和对地观测中要求卫星在一定的干扰下实现高精度的对地指向，更需要高精度的姿态控制。近年来，卫星姿态控制领域取得了许多成果，如经典的PID控制[1-2]、最优控制[3]、鲁棒控制[4-5]、自适应控制[6-7]、滑模控制[8]、模糊控制等。

其中滑模控制本质是一类特殊的非线性控制，在控制过程中，系统的状态沿着滑动模态运动，由于滑动模态可以设计且与系统参数变化和外界扰动无关，因而具有很好的鲁棒性。但在实际系统中，状态轨迹一般不会完全沿着滑模面运动，而是在滑模面两侧来回穿越，产生抖动。对航天器来说，这种抖动不仅会影响系统的控制精度，增加航天器的能量消耗，也有可能会激发系统的高频未建模动态，使系统产生振荡甚至失稳。国内外许多学者从不同的角度提出了解决的方法。文献[9]改进了滑模切换函数，提出了边界层的概念，在边界层外采用滑模切换函数，而在边界层内使用饱和函数替代切换函数，通过减少切换增益来减小抖振。然而在系统存在参数不确定性和外界存在扰动时，边界层的方法会产生稳态误差。同时传统的滑模控制中系统的相轨迹分为到达段和滑模段，系统只有处于滑模段时，才表现出对于参数变化和干扰的鲁棒性。基于此，文献[10-11]将积分项引入了滑模面的设计中，利用积分滑模的积分特性和全局滑模特性消除稳态误差和缩短到达滑模时间。

上述控制方法仅使系统渐进稳定，即闭环系统状态要在时间趋于无穷大时才能收敛为零。有限时间控制是近年来新兴的热门控制方法，相比传统的控制方法，闭环系统状态可以在有限时间收敛到零，同时具有更快的收敛特性，在工程应用中具有发展前景。文献[12]针对不存在和存在扰动力矩的两种情况设计了两种基于修正罗德里格斯参数(MRP)描述刚体航天器姿态的有限时间控制律。文献[13]基于欧拉角描述的航天器姿态模型，设计了使闭环控制系统具有负齐次性的有限时间控制律，该方法针对系统扰动和不确定性具有一定的鲁棒性。

本文综合有限时间控制和滑模控制的特点，在滑模面的设计中加入有限时间控制算法，同时应用自适应方法设计了动态滑模切换函数增益，提出了一种有限时间自适应积分滑模控制方法。该方法相较于常规滑模控制方法，系统状态收敛更快，而相较于常规有限时间方法，鲁棒性更好。数值仿真表明了该方法的有效性。

1 航天器姿态跟踪数学模型

建立四元数表示的航天器姿态跟踪模型如下[14]：

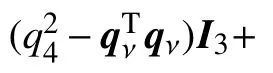
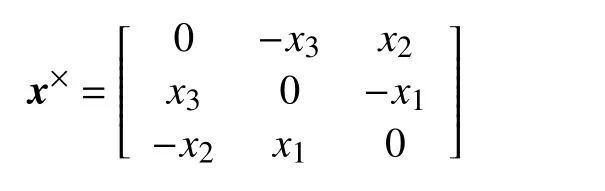
2 有限时间稳定定理

定义 1(强稳定性)[15]考虑非线性系统：

1)z(t)=x(t) ∀t∈[0,t1)

2)‖z(t)‖≤B(α) ∀t≥0

3)‖z(t)‖＜ε ∀t≥T(α,ε)

则x=0为 系统(5)的强稳定平凡解，当D=Rn时，系统为全局强稳定。

定义 2(有限时间稳定)[16]考虑非线性系统：

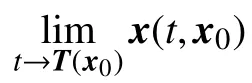
定义 3(向量函数齐次性)[17]考虑如下向量函数，f(x)=(f1(x),f2(x),···,fn(x))T:Rn→Rn，若对任 意 的 ε＞0 ， 存 在 (r1,r2,···,rn)∈Rn， 其 中ri＞0，i=1,2,···,n， 使得f(x)满足：

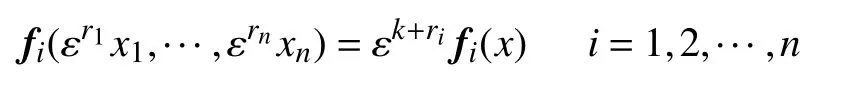
式中，k＞-min{ri,i=1,2,···,n}， 则称f(x)关 于(r1,r2,···,rn) 具 有齐次度k， 其中 (r1,r2,···,rn)称为扩张。

定义 4(标量函数齐次性)[18]考虑如下连续函数，V(x):Rn→R， 若对任意的ε ＞0 ， 存在σ ＞0和扩张(r1,r2,···,rn)∈Rn， 其中ri＞0，i=1,2,···,n，使得：

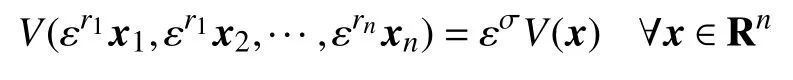
则称V(x)关 于(r1,r2,···,rn) 具 有齐次度σ。

引理 1[19]对于非线性系统(6)，若该系统是全局渐进稳定的且具有负的齐次度，那么该系统是全局有限时间稳定的。

3 有限时间自适应积分滑模控制

3.1 无扰动时有限时间控制器设计

不考虑外界干扰和转动惯量不确定性的标称航天器姿态跟踪动力学方程为：

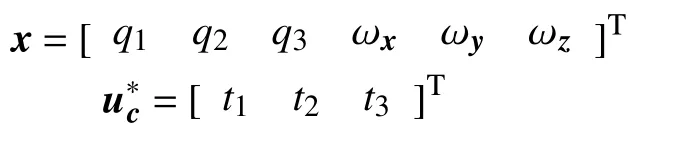
则系统(7)和系统(8)可改写成如下形式：

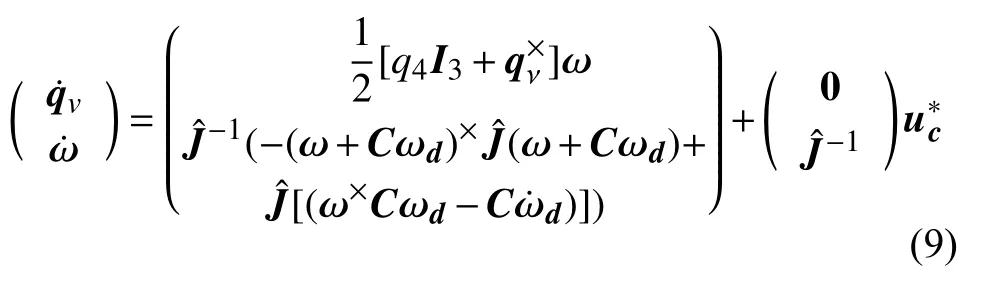
为方便控制律的设计和证明，对式(9)进行坐标变换。定义新的状态变量如下：

令：

则有：

对上式移项并对ω 求导，可得：

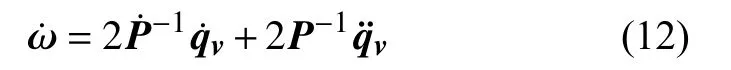
将式(12)代入式(9)，得：

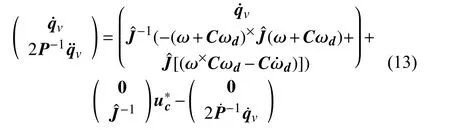
对上式进行变换如下：

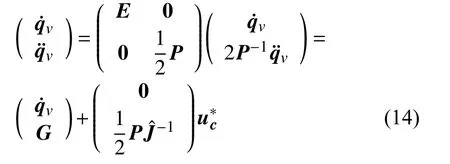
式中，

证明：将控制律式(15)带入式(14)，得：

考虑备选Lyapunov函数：

不难验证V(z)是 正定的，且当z≠0时是连续可微的，V(z)沿闭环系统(16)的解对时间的导数为：

4 数值仿真

为了验证本文方法的有效性，采用文献[20]的线性滑模面代替积分滑模面，设计控制律和3.1、3.3节的控制律分别进行数值仿真并比较。刚体航天器及控制律各项参数如下：Jˆ=diag(900,600,300)kg·m2为 惯量阵标称值，不确定性ΔJ取标称值的2%，外部干扰力矩ud=(50sin(0.1t),50sin(0.5t),50sint)N·m ，初始姿态误差四元数为q=[0.9515,0.2685,0.1449,0.0381]T，对应的姿态误差欧拉角为angle=[20◦,30◦,10◦]T，初始误差姿态角速度为ω(0)=[0.01,0.01,0.01]Trad/s，初始期望姿态四元数为qd(0)=[1,0,0,0]T，期望的姿态角速度为ωd=[0.03sin(0.1t),0.03sin(0.1t),0.03sin(0.1t)]Trad/s，控制参数取α1=0.5，k1=k2=k=1，a=0.01，c=10。

首先考虑无外界扰动和航天器转动惯量确定的情况，为方便比较，将误差四元数转换成按3-2-1转序得到的误差姿态角，仿真结果如图1～图3所示。

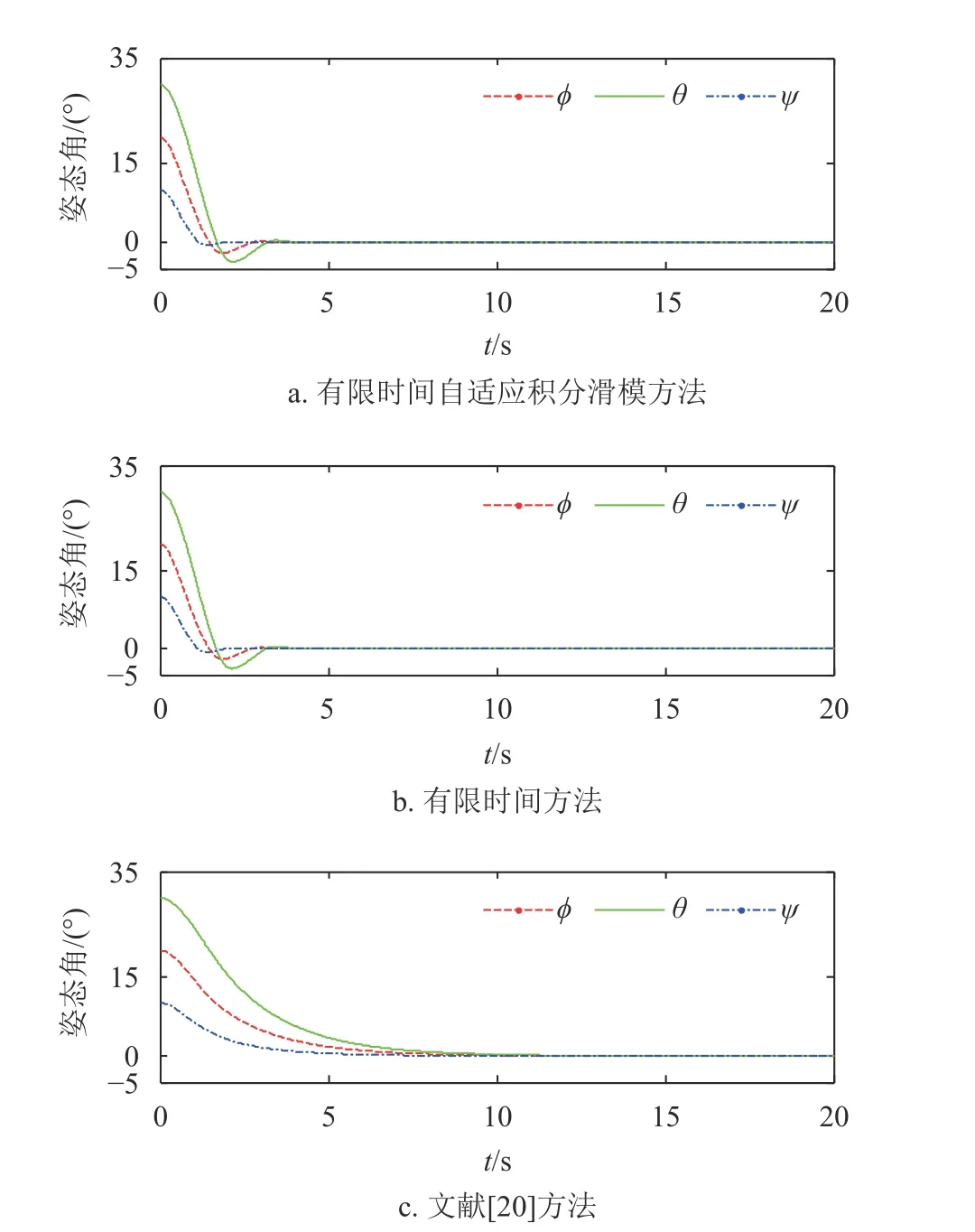
图1 无扰动时3种方法误差姿态角比较

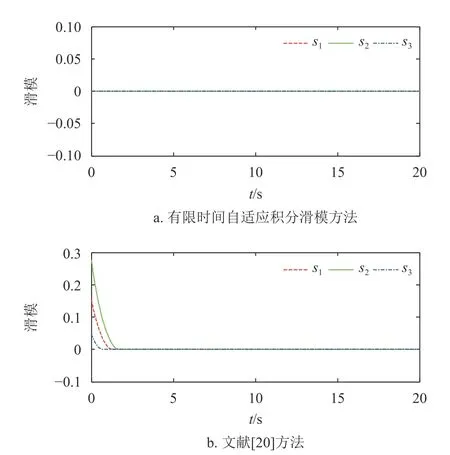
图3 无扰动时滑模方法滑模面比较

图1、图2为3种方法的误差姿态角和误差姿态角速度仿真结果，从图中可以看出，3.3节提出的有限时间自适应积分滑模方法能够使得误差姿态角和误差姿态角速度在有限时间收敛到零，在没有外界扰动和航天器转动惯量确定的情况下，与本文3.1节提出的有限时间算法结果基本相同。这是因为在积分滑模面的设计中，将有限时间控制的系统状态运动轨迹作为期望的滑动模态的导数，当系统保持在滑模面上时，状态运动轨迹便与有限时间算法相同。两种方法收敛速度均快于文献[20]，原因是文献[20]使用线性滑模面，因此系统状态只能是指数收敛，在时间趋于无穷大的时候状态收敛到零。

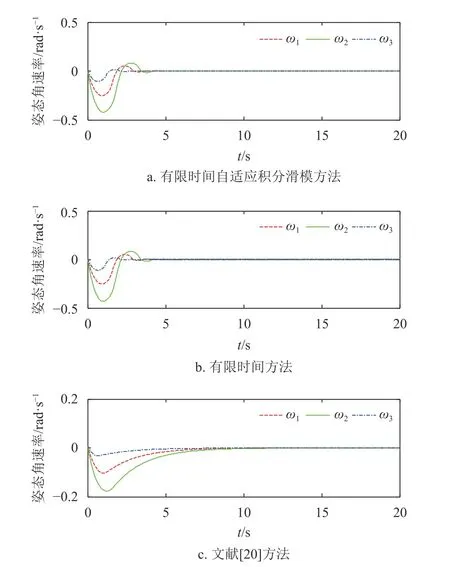
图2 无扰动时3种方法误差姿态角速度比较

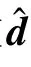
在考虑外界扰动以及航天器转动惯量存在不确定性的情况下，仿真结果如图4～图6所示。

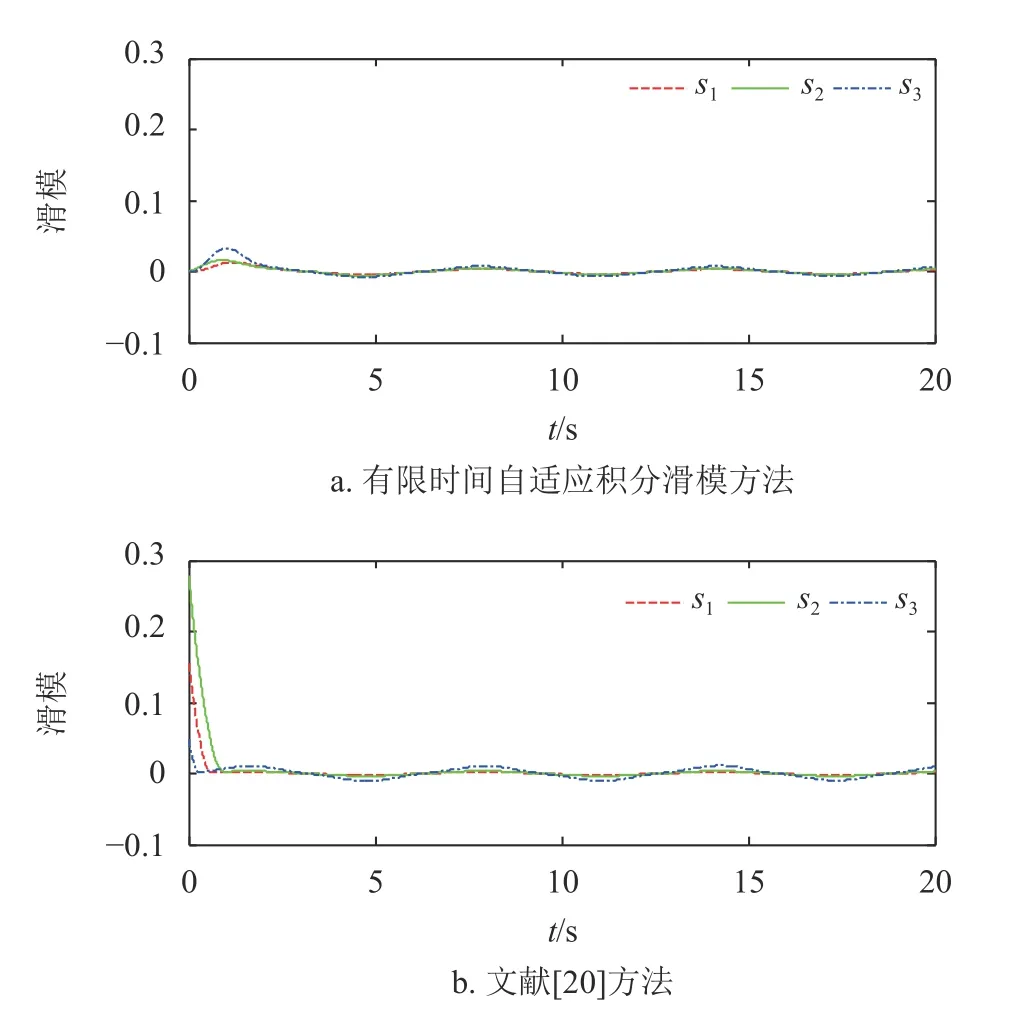
图6 有扰动时滑模方法滑模面比较

从图4和图5中可以看出，在存在外界扰动和航天器转动惯量存在不确定性的情况下，3.3节提出的有限时间自适应积分滑模方法能够克服聚合扰动，使得误差姿态角和误差姿态角速度仍在有限时间内收敛，体现了一旦系统运行在滑动阶段，滑模控制具有对外界干扰和参数不确定的不敏感性特点。而3.1节和文献[20]的方法都只能使得误差姿态角和误差姿态角速度在零点附近波动，前者的收敛速度更快，这是因为有限时间控制方法相比线性指数控制方法具有更快的收敛性[21]。

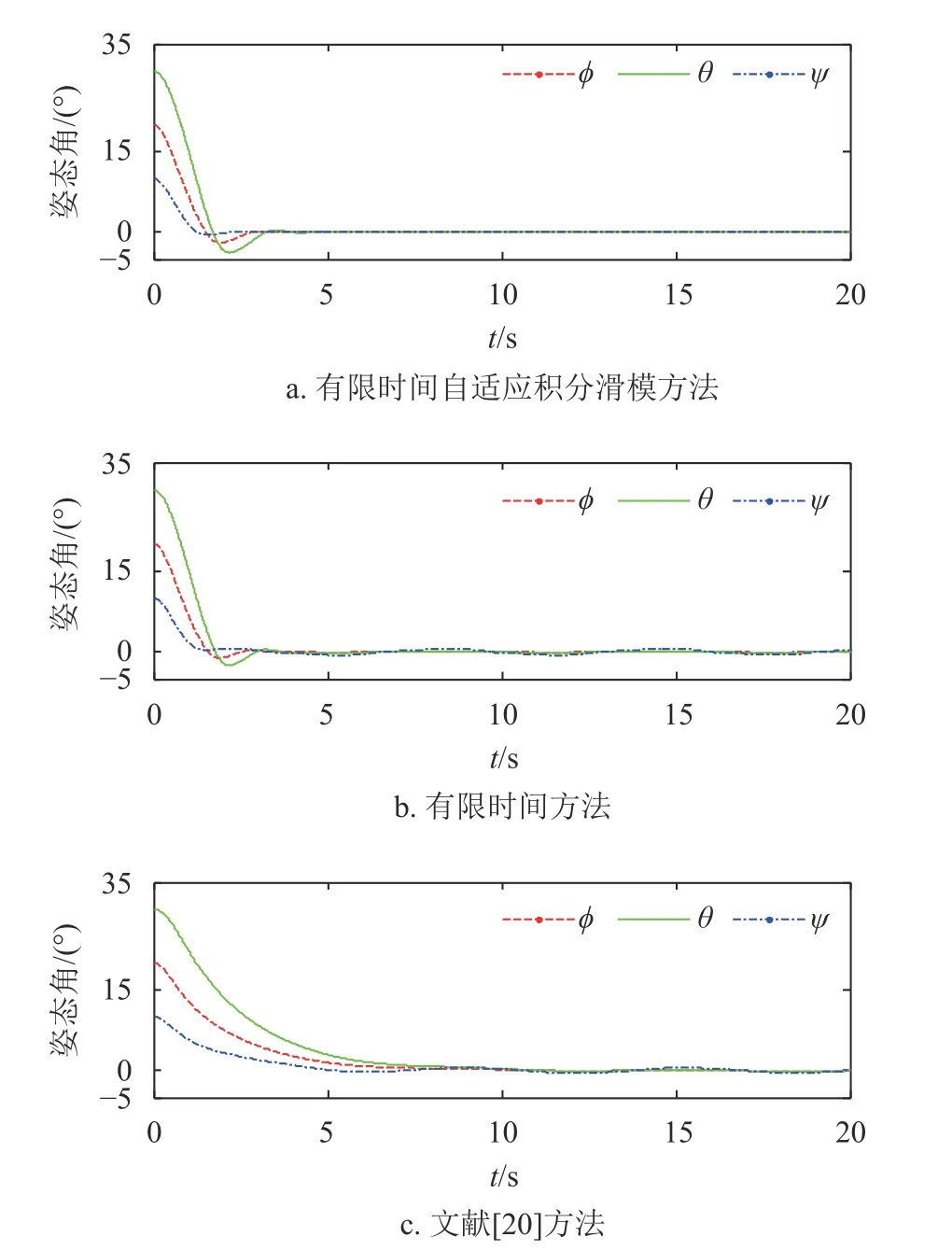
图4 有扰动时3种方法误差姿态角比较

图5 有扰动时3种方法误差姿态角速度比较

考虑到工程上的可实现性，使用了连续函数f(s)代 替切换函数s gn(s)。从图6可以看出，在聚合扰动存在的情况下，传统滑模面和积分滑模面都不能收敛到零，只能收敛到边界层以内(本文仿真取边界层a=0.01)，但积分滑模的全局滑模的特点使得积分滑模面能够迅速收敛到边界层内。

图7 有扰动时自适应参数

5 结 束 语

考虑存在模型参数不确定和外界干扰的情况，本文建立了用四元数表示的航天器姿态跟踪数学模型，提出了一种有限时间自适应积分滑模控制方法。首先针对无参数不确定性和干扰的情况，设计了一种有限时间控制器，保证航天器姿态在有限时间跟踪上期望姿态。在考虑扰动的情况下，结合有限时间控制和滑模控制设计了一种积分滑模面，利用自适应方法动态调整切换函数增益，在线辨识聚合扰动的上界。该方法兼具有限时间控制和滑模控制的优点，可使闭环系统状态有限时间收敛并具有很好的鲁棒性。理论分析和仿真结果说明了本文方法的有效性。