基于稀疏字典学习的VLSI温度场重构技术

张天一，李文昌*，肖金玉，刘 剑

(1. 中国科学院半导体研究所 北京 海淀区 100083；2. 中国科学院大学微电子学院 北京 石景山区 100049；3. 华润上华科技有限公司 江苏 无锡 214028；4. 中国科学院大学材料科学与光电技术学院 北京 石景山区 100049)

随着集成电路工艺的发展，晶体管的特征尺寸越来越小，多核处理器等超大规模集成电路(very large scale integration, VLSI)单位面积上集成的器件越来越多，导致芯片功率密度增加，工作温度上升，从而引起严重的热问题。过高的温度会降低芯片的运行性能，减少芯片的使用寿命，严重时甚至导致芯片直接损坏[1-2]。高性能芯片采用动态热管理(dynamic thermal management, DTM)技术处理热问题[3-4]。DTM通过集成在芯片上的温度传感器监测芯片温度场信息，当芯片温度超过阈值时，触发管理机制并采用调整芯片工作负载、降低时钟频率或者启动冷却装置等方式降低芯片温度，可以有效地抑制芯片过热的情况发生[5]。温度场监测精度对DTM准确、高效运行至关重要。温度场监测误差会导致DTM过早或过晚触发。不必要地过早触发DTM会使芯片低性能运行；而延迟触发DTM则可能导致芯片的温度过高，甚至导致芯片失效。因此，精确监测芯片温度场对于保障芯片运行性能和可靠性十分必要。

在实际应用中，受芯片资源限制，只允许少量温度传感器布置在被监测芯片上。因此，如何通过有限数量的温度传感器精确地获得温度场信息成为研究热点[6-7]。文献[8]利用奈奎斯特-香农采样定理，通过频域傅里叶分析技术实现了多核处理器的温度场重构，研究证明温度场在频域表现为稀疏性，所谓稀疏性即大部分数据为零或者接近零，非零数据的个数称为稀疏度。文献[9]通过离散余弦变换在频域分析温度场先验信息，并利用频域信号能量特性提出了温度传感器布局与温度场重构策略，相比于傅里叶变换，离散余弦变换在频域具有更好的能量集中性。文献[10]在频域分析的基础上，通过改进Voronoi图构建算法来提高温度场重构精度。在频域下，温度场信号主要集中在低频区，因此基于频域的温度场重构技术在重构温度场时会忽略大部分高频信号，这在一定程度上会造成重构精度的降低。文献[11]提出了基于压缩感知的温度场重构技术，利用温度场频域稀疏性并结合压缩感知理论还原温度场，但需要注意的是，根据压缩感知理论当温度传感器数量小于稀疏度时，重构精度会降低。除了频域法，文献[12]提出了基于主成分分析法(principal component analysis, PCA)的温度场重构技术，将温度场用线性模型表示，但是线性模型为欠完备字典，会损失一部分信息。

本文提出一种基于稀疏字典学习的温度场重构技术。首先利用温度场先验信息训练字典，然后通过字典学习将温度场进行稀疏表示，并将温度传感器布局转化为NP-hard问题，采用模拟退火算法求解传感器位置，最后利用正交匹配追踪算法重构温度场，提高温度场重构精度。

1 温度场稀疏编码

许多高性能芯片在不同工作条件下，产生的温度场分布不同，在芯片设计阶段可以得到温度场分布的先验信息。通过对温度场先验信息进行字典学习，可以将温度场稀疏表示[13]。假设温度场先验信息包含T个温度场，对于1≤t≤T，温度场ft是一个W×H的离散化数据矩阵，W、H分别代表温度场宽和高方向的离散数据分辨率。记N=W×H，对于0≤n≤N-1，将温度场矩阵ft转换为向量表示：

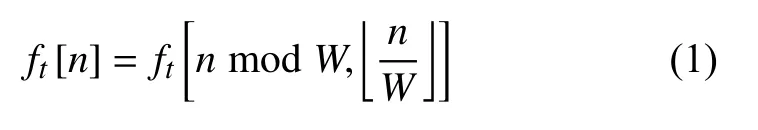
式中，D称为字典，D={d1,d2, ···,dK}，是由一组基向量组成的N×K矩阵，每个基向量称为原子；K为原子个数，当用于稀疏表示时，D为过完备字典，即K＞N；X={x1,x2, ···,xT}，是F的稀疏编码，当稀疏度为R时，X的每个列向量中只有R个非零值。

图1 温度场重构过程

求解字典D为一个迭代过程，每次迭代需要完成稀疏编码和字典更新两个步骤，直到完成迭代次数，流程如图2所示。

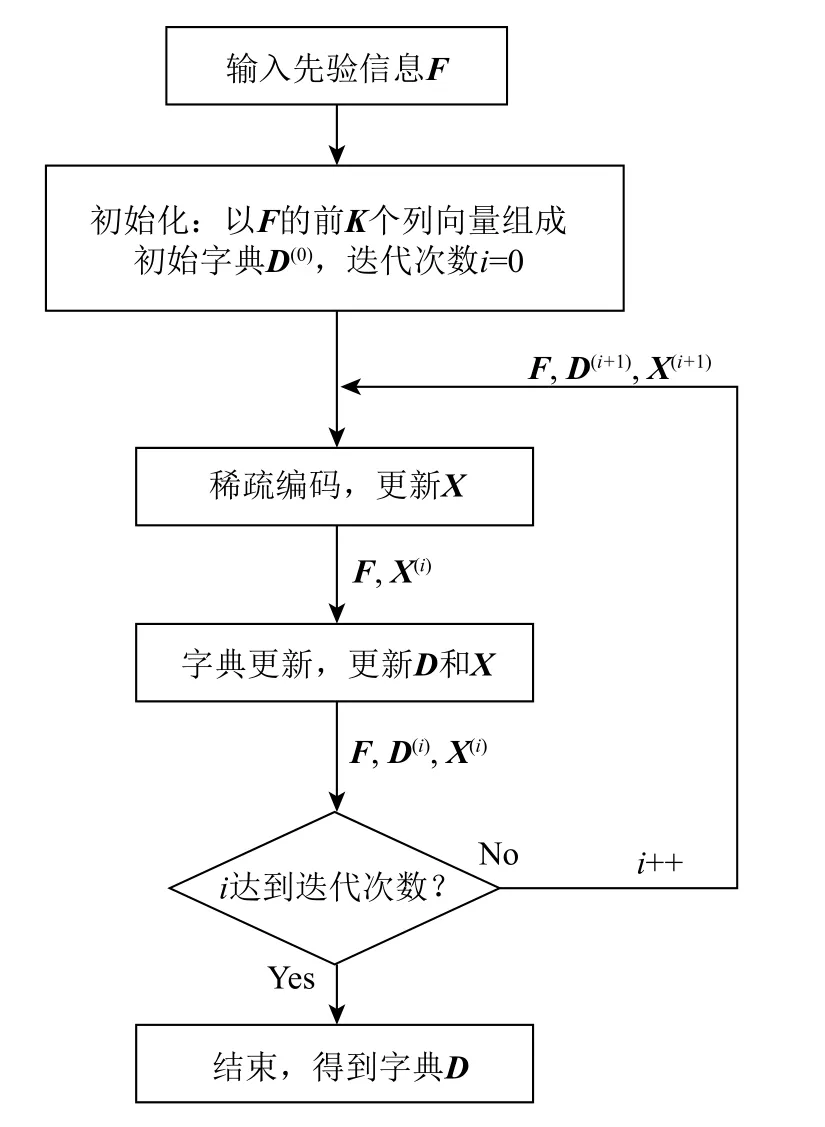
图2 字典D的求解流程

稀疏编码，即为已知字典D更新X的过程，采用逐列更新方式，对于X的第t列xt，以最小均方误差作为原则，求解可以表示为：

式中，下角标F代表Frobenius范数。由于ft、D及xt的稀疏度R均是已知的，可以利用正交匹配追踪算法计算[14]。X的完整更新算法过程如下：

1) 已知字典D、先验信息F、稀疏度R；

2) 当更新X的第t列，初始化：残差r0=ft；索引集Φ = ∅；i= 1；

3) 判断：当i≤R时进行下一步，否则跳至步骤9)；

4) 求D每列与残差ri-1的内积，并从其中找出最大值对应的位置λi，即：

5) 更新索引集Φ =Φ∪{λi}，根据索引集中的角标位置从D中提取相应位置列向量组成矩阵Di={dλ1,dλ2, ···,dλi}；

6) 根据最小二乘原理求得稀疏表示：

式中，符号“†”表示广义逆矩阵运算，即：

式中，符号“*”代表矩阵的共轭转置运算。

7) 更新残差ri，ri=ft-Dixi；

8) 完成本次迭代，i=i+ 1，跳至第3)步；

9) 完成X的第t列更新，xt[Φ] =xi，跳至第2)步并重复步骤3)～8)，直至X的所有列更新完毕。

字典更新，即为已知X更新D的过程，逐个更新字典原子，对于D的第k个原子满足最小二乘原则：

式中，xT表示X的行向量；上角标j、k表示第j、k行；Ek代表更新第k个原子时对应的残差矩阵。此时可以利用奇异值分解求解dk。对Ek进行奇异值分解，取左奇异矩阵的第1个列向量作为dk，取右奇异矩阵的第1个行向量与第1个奇异值的乘积作为xTk，则完成了对第k个原子的更新，同时更新了X。D的完整更新算法过程如下：

1) 已知原字典D，先验信息F，稀疏编码X；

2) 更新第k个原子，找到xTk中非零元素的位置索引集合Λ；

3) 令dk= 0，并计算残差矩阵：

6) 同时更新dk及xTk：

dk=U[:,1]xTk[Λ]=Σ[1,1]V[:,1]*

7) 跳至第2)步并重复步骤3)～6)，直至D的所有原子更新完毕。

完成图2的流程后得到字典D，然后就可以利用字典D计算温度传感器位置，并实现温度场重构。

2 传感器分配与温度场重构

如图1所示，根据温度传感器数据计算出X。对于s个温度传感器，温度传感器的位置记为L={l1,l2, ···,ls}，可以得到：

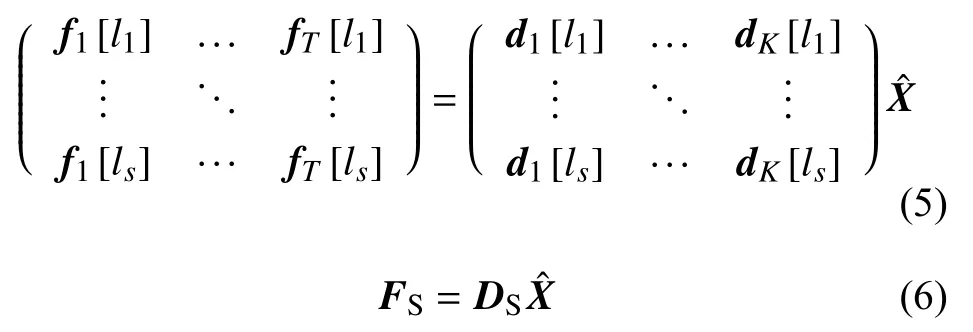
温度传感器的位置会影响X的解算精度。考虑实际温度传感器的采样噪声以及X的求解误差，式(6)的表达式调整为：

式中，δ为随机噪声；ε为求解误差。对式(7)进行分析可以得到如下关系：

根据式(8)，求解误差ε的大小被矩阵DS的条件数Cond2(DS)限制，因此，选出s个温度传感器位置，使Cond2(DS)最小就能使求解误差最小。从N个位置中选出最优的s个位置，这是NP-hard问题。本文采用模拟退火算法求解该NP-hard问题[15]。为了不使X的求解变为不适定问题，温度传感器数量s与稀疏度R应满足s＞R，同时矩阵DS的秩应不小于R，即rank(DS) ≥R。传感器位置完整更新算法过程如下：

1) 已知字典D；

2) 初始化模拟退火参数：初始温度Tin，终止温度Tstop，温度衰减指数γ，内循环次数M；

3) 随机生成s个位置L和Lc，分别为最优解和当前解，如果rank(DS)≥R且rank(DSc)≥R，则分别计算DS和DSc的条件数C和Cc，否则重复该步骤；

4) 令初始温度T=Tin，开始模拟退火，当T＜Tstop时，跳至第11)步；

5) 执行内循环，完成步骤6)～9)M次；

8) 生成随机数 θ∈(0,1)，计算Metropolis准则概率：

10) 更新当前温度T，T= γT，跳至第4)步；

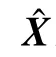
3 实 验

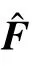
图3 实验原理

实验中，TTC包含225个基本单元即传感器备选位置为225个，每个温度场离散为W×H= 15×15的二维矩阵，相应的温度场分辨率N= 225。先验信息由300个温度场组成，T= 300。在进行字典学习时，选取的字典原子个数K= 250。利用有限数量温度传感器重构温度场的性能，对比温度传感器数量s= 7, 9, ···, 17, 19时重构温度场与先验信息之间的平均误差、均方误差和误报率。

平均误差Eavg，即温度场重构误差的平均值，其值越低表示重构精度越高，定义为：

均方误差EMSE，即温度场重构误差平方的平均值，其值越低表示重构精度越高，定义为：

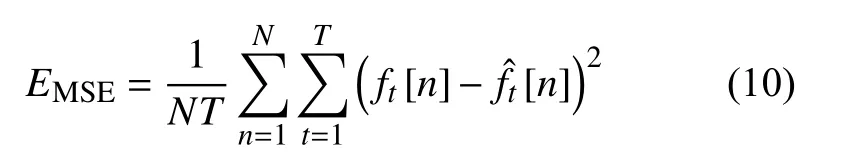
误报率(false alarm rate, FAR)，定义为漏报或虚假紧急情况所占的比例[16]。漏报表明实际温度已经达到DTM的报警阈值，但重构温度却低于该值；虚假紧急情况表明实际温度尚未达到报警阈值，但重构温度已高于该值。FAR越低意味着温度场重构精度越高，表达式为：

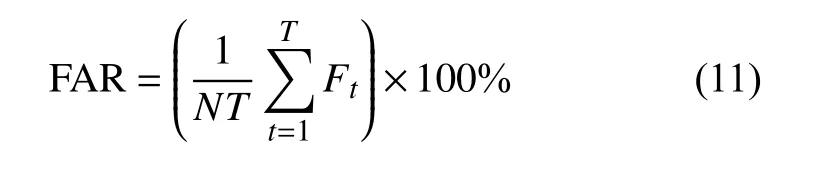
式中，Ft表示第t个温度场中发生误报的次数。这里选取的阈值为50 ℃。

使用性能变化的相对率对比不同方法的性能，定义为：

式中，X1、X2分别表示方法1、方法2的X性能，本文中X包括Eavg、EMSE和FAR。

将Voronoi图方法[10]、K-LSE方法[11]、PCA方法[12]与本文提出的方法进行比较，结果如图4～图6所示。可以看出，4种方法的温度场重构精度随温度传感器数量的增加而提升。表1列举了不同方法的平均重构性能，本文提出的方法在Eavg、EMSE和FAR方面均优于Voronoi图和K-LSE方法。相比Voronoi图方法，Eavg、EMSE和FAR平均提升了1.5 ℃、9.7和10.5%，相对提升了39.6%、46.7%和36.2%；相比K-LSE方法，Eavg、EMSE和FAR平均提升了0.9 ℃、5.4和7.3%，相对提升了28.5%、32.7%和28.3%。

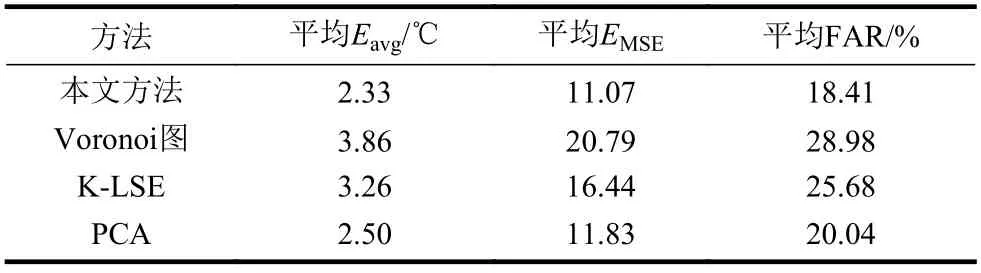
表1 不同方法性能对比

图4 不同方法Eavg对比

图6 不同方法FAR对比

相比PCA方法，本文方法Eavg、EMSE和FAR平均提升了0.2 ℃、0.8和1.6%，相对提升了6.8%、6.4%和8.1%，稍优于PCA方法，但随着温度传感器数量的增加，本文方法重构性能更加优越。上述结果表明，本文提出的方法重构温度场更精确。

图5 不同方法EMSE对比

鉴于芯片设计阶段的算法均离线实现，因此温度场重构完成时间主要由芯片工作阶段的算法运行时间决定。为了比较不同方法的收敛速度和计算量，将不同算法的运行时间进行对比。所有方法均在上位机运行，上位机配置为：Core i7-9700处理器；3.00 GHz主频；16.00 GB内存，实验结果如图7所示。Voronoi图方法由于需要进行数次域变换，算法的运算时间最长。本文方法与K-LSE方法的运算时间接近，略高于PCA方法。综合考虑重构精度及运算时间，本文方法更具有优势。

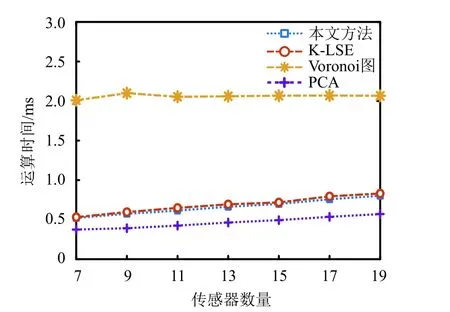
图7 不同方法运算时间对比

下面分析使用本文方法时，稀疏度R的设置对重构精度的影响。实验设定温度传感器数量s=15，然后对比R从5变化到14时温度场的重构性能，结果如图8所示。随着稀疏度R增加，温度场重构精度呈上升趋势。这是由于稀疏度的增加意味着使用了更多的字典原子，可以还原的温度场细节随之增多。需要注意的是，R接近s时，性能的提升不再明显。另一方面，考虑到R的增加也会导致稀疏编码X求解时迭代次数的增加，这会加重计算负担。所以R应避开较大和较低值，综合考虑设定适中值。

图8 稀疏度影响的分析

4 结 束 语

本文提出了一种基于稀疏字典学习的温度场重构技术。通过字典学习方法将温度场先验信息稀疏编码，然后用模拟退火算法计算温度传感器位置分布，利用正交匹配追踪算法计算稀疏编码，从而实现温度场重构。结果表明，相较基于频域分析的方法，本文提出的方法能够提高温度场重构精度，同时占用较低的运算时间，具有更优越的温度场重构性能。