脉间波形幅相联合设计抗欺骗干扰方法

葛萌萌，余显祥，严正欣，方学立，崔国龙*，孔令讲

(1. 电子科技大学信息与通信工程学院 成都 611731；2. 复杂航空系统仿真重点实验室 北京 丰台区 100076)

现代电子战中，各类干扰技术快速发展，从箔条类的无源干扰到噪声压制、假目标欺骗的有源干扰[1-2]，使得现代雷达的生存环境越来越复杂，严重降低了雷达的生存性能。为了保证雷达在干扰环境下正常工作，雷达抗干扰技术得到了广泛关注与研究[3-5]。

波形设计作为一种典型的雷达抗干扰手段，主要分为抗距离欺骗干扰和抗速度欺骗干扰两方面。针对距离欺骗干扰，文献[6]利用波形分集技术，在不同脉冲重复时间(pulse repetition time, PRT)发射相互正交信号，并利用匹配滤波抑制距离欺骗干扰，但是该方法采用的正交波形会导致较高的距离旁瓣。文献[7]从低截获抗干扰角度出发，通过对线性调频-频率编码复合波形设计滤波器抑制距离旁瓣，进一步提高了线性调频-频率编码复合波形的低截获抗干扰能力。文献[8]针对切片重构干扰和频谱弥散干扰导致的距离维假目标，通过最小化发射信号与干扰信号的互相关积分电平(integrated level,IL)和发射信号的自相关积分旁瓣电平(integrated sidelobe level, ISL)的加权和，在恒模约束下，设计发射波形，有效抑制了这两种干扰类型。文献[9]针对间歇采样干扰，通过建立最小化目标信号与接收滤波器的ISL和干扰信号与接收滤波器的IL的加权和的优化准则，在PAR约束下，采用交替方向乘子法(alternation direction method of multipliers,ADMM)联合设计发射波形与接收滤波器实现间歇采样干扰抑制，但是该算法无法保证收敛性。另一方面，针对速度欺骗干扰，文献[10]通过设计脉冲初相有效地对抗速度欺骗干扰。该方法考虑恒模约束，建立最小化干扰阻带内能量的优化问题，利用共轭梯度法求解最优脉间初相，极大地改善了脉冲多普勒雷达在速度欺骗干扰环境下的目标探测性能。在此研究基础上，文献[11-12]分别利用修正牛顿法和WeCAN算法求解文献[10]中的优化问题。但是，文献[11]的工作仅涉及脉间初相，未考虑脉间幅度设计，没有充分利用幅度这一自由度；同时，相比离散量化相位，连续相位设计在实际工程应用中较为困难。

对此，本文增加脉冲幅度这一自由度，同时考虑离散相位，研究脉间波形幅相联合设计抗速度欺骗干扰方法。通过将最小化阻带内干扰能量与目标旁瓣能量的加权和作为优化准则，在离散量化相位和PAR约束下，构建幅度-相位联合设计抗速度欺骗干扰的优化问题。然后，根据交替方向惩罚法(alternating direction penalty method, ADPM)框架，提出IADPM算法求解该优化问题，具体地，通过引入辅助变量将原优化问题分解为一系列子问题，每个子问题利用不同算法求出近似解，进而不断循环迭代，求出最优幅度和相位，最终实现脉间幅度相位联合设计抗速度欺骗干扰。

1 信号模型

假设脉冲多普勒雷达在一个CPI内发射N个不同幅度和初相的脉冲信号，第n个脉冲发射信号为：

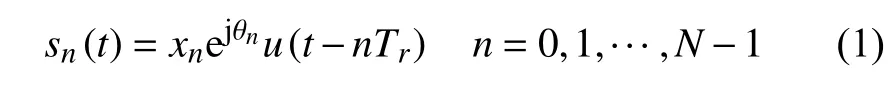
式中，xn和 θn分 别为第n个脉冲信号的幅度和初相；Tr为 脉冲重复时间；u(t)定义为：

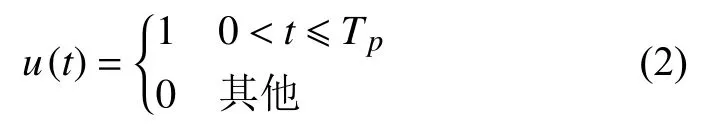
式中，Tp为脉冲宽度。

假设在某一距离单元内，有Q个不同多普勒频率的目标，因此，第n个脉冲接收到的目标回波为：

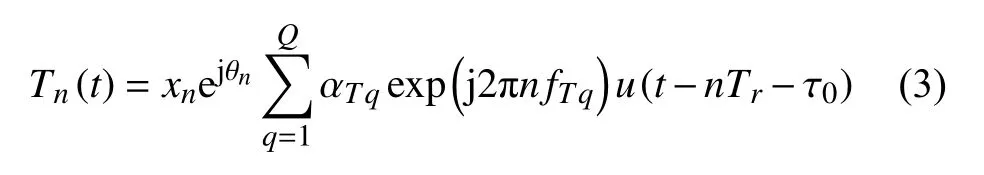
式中， τ0为 目标双程时延； αTq为 第q个目标的回波幅度；fTq=2vTqTr/λ为 第q个目标的归一化多普勒频率；vTq为 相应的目标速度；λ为雷达工作波长。

数字射频存储器(digital radio frequency memory,DRFM)干扰机截获到雷达信号后需要对信号进行分选识别，调制虚假多普勒信息形成干扰信号后转发出去，一般假设DRFM干扰机发射的脉冲信号滞后真实雷达信号i个PRT[10]，如图1所示。

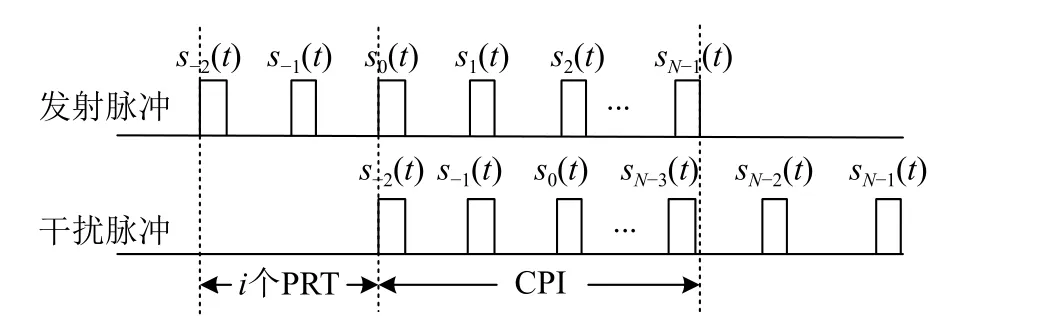
图1 干扰脉冲示意图

假设在时延 τ0处 ，DRFM干扰机调制了P个不同多普勒频率的虚假目标，则第n个脉冲接收到的干扰回波为：

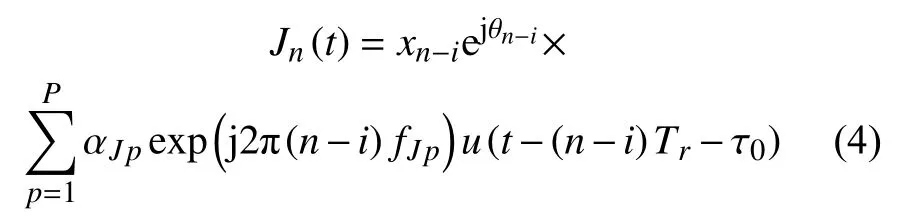
式中， αJp和fJp分 别为第p个虚假目标的幅度和归一化多普勒频率。

因此，第n个脉冲的接收回波为：

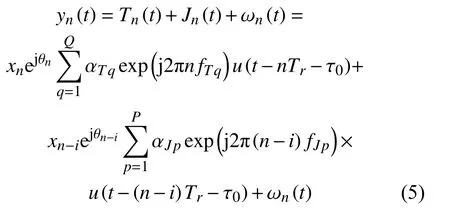
式中，ωn(t)表示加性高斯白噪声信号。

经过匹配滤波处理后，在时延 τ0处 ，第n个脉冲的输出为：

式中， υ(n)为 ωn(t)的滤波输出值，满足均值为0，方差为σ2的高斯分布。

2 问题描述

利用文献[10]中的多通道处理技术，获取目标和干扰信号的多普勒先验信息。假设干扰信号与目标信号的多普勒频率均在阻带范围内，设置阻带范围为：

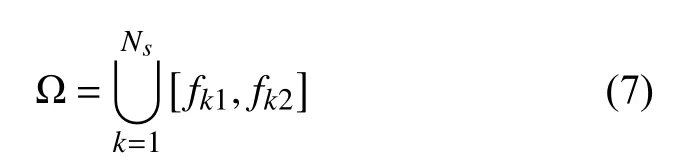
式中，∪ 为取并集操作；Ns为 阻带个数；fk1和fk2分别为第k个阻带的下限和上限频率。

根据文献[13]，忽略干扰回波幅度 αJp，可以推导出P个干扰信号在阻带内的能量为：

式中，( ·)H表示共轭转置操作；s表示为：

式中，( ·)T为转置操作。矩阵RJ的第(m,n)个元素表示为：

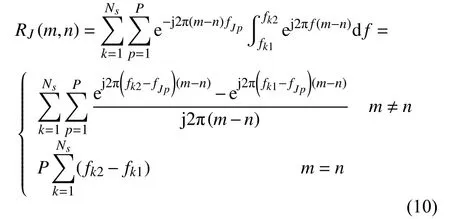
相似地，Q个目标信号在阻带内的旁瓣能量可以推导为：

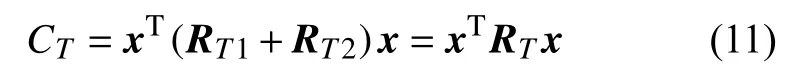
式中，x=[x0,x1,···,xN-1]T；RT1和RT2中 的第(m,n)个元素分别表示为：

式中，Δf=1/N为归一化多普勒频率间隔。

令：

因此有：

式中，| ·|为 取模操作；⊙ 为哈达玛积；J为循环移位矩阵，定义为：

为了抑制欺骗干扰，需要使干扰信号在阻带范围内能量尽可能小，同时也要保证目标信号在阻带范围内的旁瓣能量尽可能小。同时，为了避免波形的非线性失真，考虑PAR约束，可以构造以下优化问题：

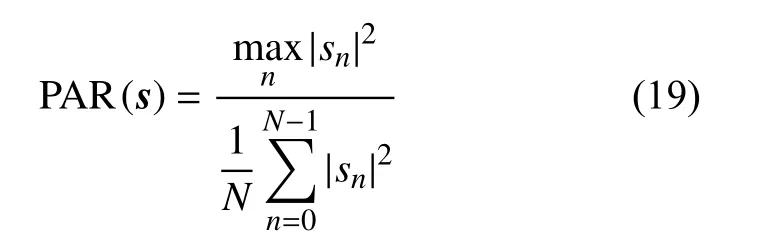
3 基于IADPM的脉间波形设计

本节提出了IADPM算法求解问题 P0。该算法的核心思想是通过引入辅助变量将原问题转换为一系列子问题，通过对每个子问题求取非精确解并不断交替循环迭代，最终求解包含幅度与相位的序列s。

3.1 算法描述

将式(15)～式(16)带入问题 P0中 ，问题 P0可进一步写为：

式中，RN为N维实向量集合。

基于文献[15]中ADPM框架，本小节提出了IADPM算法求解问题 P1。 首先，引入辅助变量z，问题P1可重写为：

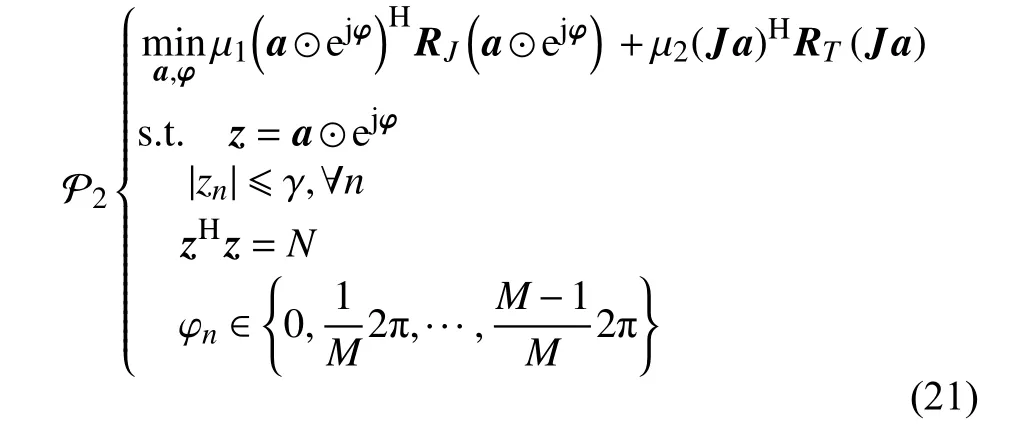
进而，构造增广拉格朗日函数：

式中，λ为拉格朗日乘子；ρ为惩罚因子；ℜ {·}为取实部操作；‖ ·‖表示二范数。

根据ADPM框架，通过交替更新z,a,φ来最小化L(a,φ,z)， 进而求得原问题的解。假设z,a,φ在第t次迭代的解分别为z(t),a(t),φ(t)，则提出的IADPM算法的迭代规则如下：

式中，δ1c和 δ2c为 接近1的两个常数，且满足0＜δ1c＜1和δ2c＞1。

首先，固定a(t-1),φ(t-1),λ(t-1),ρ(t-1)， 更新z(t)。忽略与z的无关项，式(23)可以重写为：

式(31)可以用经典的Power Method[16]方法求解，首先定义：

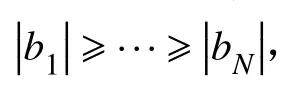
当mγ2＞N时，式(31)的解为：

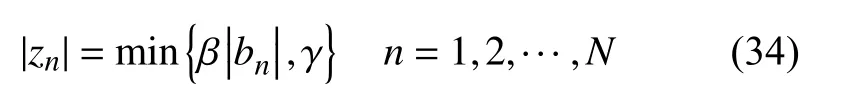
式中，

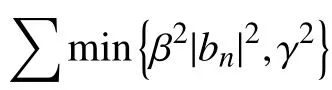
接着，固定z(t),φ(t-1),λ(t-1),ρ(t-1)，更新a(t)。忽略a的无关项，式(25)可以写为：

式中，矩阵D定义为：

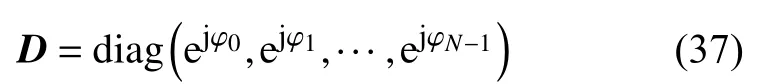
式中，d iag(···)表示将数据形成对角矩阵。

利用坐标下降(coordinate descent, CD)[17]算法求解a， 固定a0,···,ap-1,ap+1,···,aN-1，式(36)中目标函数可以表示为关于ap的表达式为：

式中，

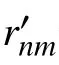
最后，固定z(t),a(t),λ(t-1),ρ(t-1)， 更新 φ(t)。忽略φ的无关项，关于φ 的优化问题可写为：

同样采取CD算法求解φ。 固定φ0,···,φp-1,φp+1,···,φN-1， 式(38)关于φp的表达式可以重写为：

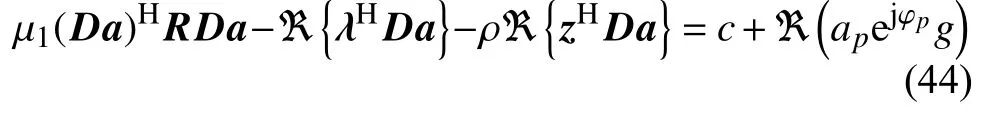
式中，

因此，式(44)关于 φp的优化问题可以重写为：

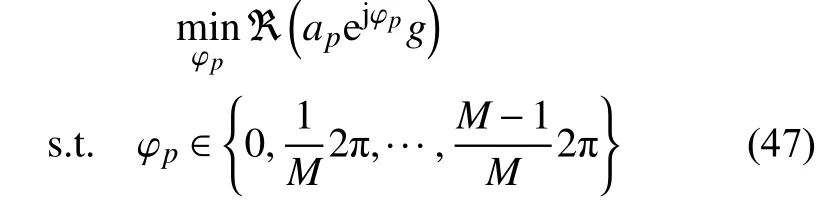
可以求得：

式中，f(ψ) 表 示最接近ψ 的离散量化相位值。

z,a,φ,λ,ρ不断迭代更新直到收敛。根据文献[18]，设置停止迭代的条件为：

IADPM算法求解问题 P0，总结IADPM算法流程如下所示。

输入：初始值z(0),a(0),φ(0),λ(0),ρ(0)， δ1c,δ2c和控制收敛的阈值ζ

输出：局部最优解a和φ；

whileϵ(t)＞ζ

判断mγ2是 否大于N，根据式(33)和式(34)更新z(t)；

根据式(42)更新；

end

forp= 1:N

end

分别根据式(29)和式(30)更新ρ(t)和 λ(t)；

根据式(49)计算ϵ(t)；

end while

求出最优序列a和 φ后 ，根据a和 φ的定义，即可计算发射脉冲串的幅度和相位序列。

3.2 计算复杂度分析

基于IADPM算法求解问题 P0的计算量主要与迭代次数和矢量z,a,φ的更新有关。其中，更新矢量z所用的Power Method计算量主要来自于二分法求 β值，相应地计算量为O(I(N))， 其中I为二分法迭代次数；更新矢量a中的计算量主要来自于计算u和v，其计算量为O(N)，遍历N个元素，其计算量为O(N2)；更新矢量 φ中的计算量主要来自于构造g，其计算量为O(N)，遍历完N个元素，其计算量为O(N2)。因此，在(I)ADPM算法一次迭代中的计算量为O(I(N))+ON2。

4 仿真实验

本节主要通过仿真实验验证脉间幅度相位捷变设计抗速度欺骗干扰方法的有效性。

4.1 算法性能分析

本小节首先对提出的IADPM算法的收敛性进行分析。考虑单目标与单干扰场景下，即P=1，Q=1，假设雷达发射脉冲个数N=512，干扰的归一化多普勒频率fJ=0.4， 目标的归一化多普勒频率fT=0.47，干扰信号滞后目标信号2个PRT，设置阻带范围为Ω=[f11,f12]=[0.3,0.5]。 随机初始化s,λ ,z的初始值与s的初始值保持一样， δ1c=0.9995， δ2c=1.0005,μ1=0.9,M=16。将ADMM算法作为对比算法[18]，其中ADMM算法中惩罚因子 ρ保持不变，其他参数迭代规则按照式(23)～式(30)所示。

图2分别展示了IADPM与ADMM算法中的残差 ϵ随迭代次数变化曲线图。可以看到，对于IADPM算法，无论惩罚因子ρ 的初始值取多少，残差ϵ 总能不断保持下降趋势直至收敛，然而ADMM算法受惩罚因子 ρ影响较大，并不能总是收敛，当ρ为1和100时，ADMM算法最后趋于收敛，然而当ρ 取值较小为0.1时，ADMM算法无法收敛。

图2 ϵ随迭代次数变化的曲线图

4.2 抗干扰结果分析

本小节针对设计的脉间幅度-相位波形序列的抗干扰效果进行仿真验证。首先考虑单目标与单干扰场景，参数设置与4.1节保持一致，设置噪声功率 σ2=0 dB，目标信号幅度 |αT|2=10 dB，干扰信号幅度| αJ|2=20 dB。

图3为单目标单干扰场景下的抗干扰结果。可以看到，由于干扰的存在，利用传统脉间波形得到的慢时域多普勒谱上，目标和干扰同时存在，且干扰幅度比目标幅度高约10 dB。相反，利用优化后脉间波形得到的多普勒谱上，可以看到干扰尖峰消失，仅剩下目标尖峰，且在 [0.3,0.5]阻带范围内存在凹槽。

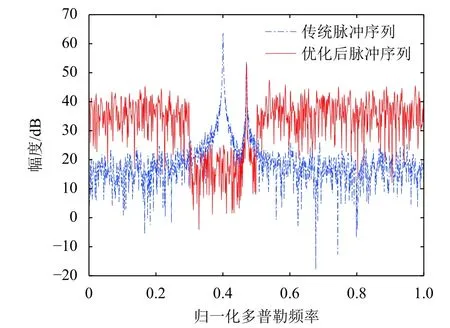
图3 单目标场景下抗干扰效果

考虑多目标与多干扰场景，设干扰个数P=2，目标个数Q=2，干扰信号的归一化多普勒频率分别为fJ1=0.35，fJ2=0.45，目标的归一化多普勒频率分别为fT1=0.42,fT2=0.44，设置阻带范围为Ω=[f11,f12]=[0.3,0.5]，其余参数保持不变。

图4给出了多目标场景下抗干扰效果图。可以看到，利用传统脉冲序列得到的慢时域多普勒谱上，两个目标和两个干扰同时存在，无法分辨真实目标。通过优化设计的脉间波形的多普勒谱上，仅剩下两个真实目标，两个干扰尖峰消失，说明了该方法在多目标多干扰场景下依然适用。

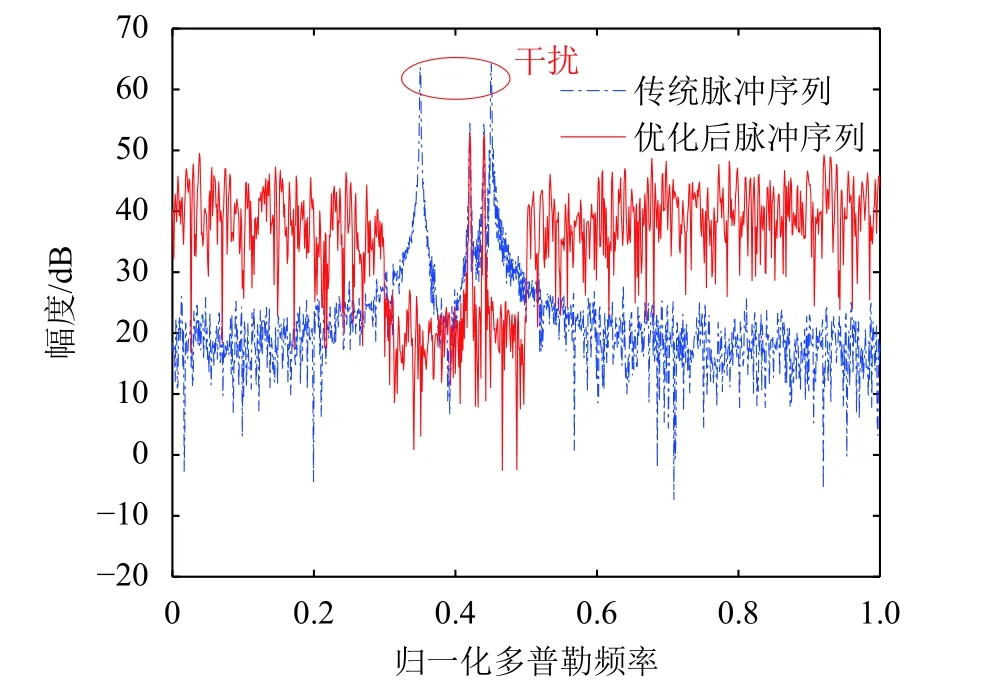
图4 多目标场景下抗干扰效果

5 结 束 语

针对速度欺骗干扰，本文通过建立最小化阻带内干扰能量与阻带内目标旁瓣能量的加权和的优化准则，考虑波形离散量化相位和PAR约束，构建了速度欺骗干扰下脉间波形幅相联合设计的优化问题，针对该优化问题，提出了IADPM算法求解，并理论分析了IADPM算法的计算复杂度。

仿真结果表明，IADPM算法在不同的惩罚因子下总能收敛，优于ADMM算法。离散相位情况下，设计的波形更加易于工程实现，同时可以有效抑制速度欺骗干扰，在多目标多干扰情况下，算法依然有效，普适性较高。