电子束尾波对质子束自调制尾波相速度影响的理论和数值模拟研究*

华津宇 盛政明2)†

1) (上海交通大学物理与天文学院, 激光等离子体教育部重点实验室, 上海 200240)

2) (上海交通大学李政道研究所, 上海 200240)

高能质子束在等离子体中通过自调制不稳定激发尾波的研究在过去的十年里有了长足的发展, 在欧洲核子研究中心(CERN)人们已经在相关AWAKE实验中利用这种尾波加速电子, 并获得了最高能量约2 GeV的电子束.针对高能粒子加速应用需求, 近几年人们又进一步提出了利用电子束种子尾波控制质子束自调制过程的方案, 用于提升尾波的强度与稳定性.本文研究了电子束种子尾波对质子束自调制尾波相速度的影响,着重讨论了导致尾波相速度改变的多种物理机理及电子束所起到的作用.通过理论分析和二维粒子模拟研究发现, 电子束的引入可以提升质子束自调制尾波的增长率和尾波的相速度, 且电子束的电荷密度越高其效果愈明显.本文还探讨了电子束能量和质子束的纵向密度分布对相速度变化的影响.

1 引 言

等离子体尾波加速概念[1,2]自从上世纪70年代末被提出以来已经取得了长足的发展, 它通过高强度的激光脉冲或者高能带电粒子束在等离子体中激发出一个大振幅且具有相对论相速度的电子等离子体波来加速电子[3−5].等离子体尾波的场强接近于所谓的等离子体波破裂幅度E0=meωpc/e,其中为等离子体振荡频率,n0为等离子体电子密度,e为电子电荷,me为电子质量,c为光速.该场强比传统加速器产生的加速电场高出好几个数量级[6], 使得等离子体尾波加速已经成为未来最有前景的新型加速方式之一, 吸引了众多国内外研究者的目光[7−9].

在众多等离子体尾波加速的方案中, 质子束尾波加速最早由Caldwell等[10]在2009年提出, 它的机制与电子束驱动尾波加速极为相似, 都是通过一束很短的带电粒子束在等离子体中激发尾波.由于质子的质量远远大于电子, 作为尾波驱动源的质子束所携带的能量也远远地超过了激光和电子束的能量, 这使得质子束驱动的尾波加速成为目前最有可能通过单级加速把轻子能量加速到TeV量级的加速方式[11].然而只有长度接近于等离子体的波长λp=c/ωp的质子束才能在等离子体中产生接近于波破的电场强度, 并且现有的技术手段却没有办法获得如此之短的高能质子束.在2010年Kumar等[12]提出了通过长质子束在等离子体中通过自调制不稳定 (self-modulation instability) 来激发等离子体尾波的概念.当一束长质子束在等离子体中传播时, 质子束本身产生的周期性横向调制会使得长质子束纵向结构发生演化, 从而产生等离子体波的截断效应, 使得质子束演变成一长串与等离子体波长相匹配的短质子束串.由此可以激发出一个非常强的电场, 用来加速外部注入的电子束.

这个理论已于2018年在欧洲核子中心(CERN)被AWAKE实验合作组证实[13,14].他们在实验中使用了一束长6 cm、中心能量400 GeV的质子束.在质子束通过长度10 m的等离子体管道之后, 高速摄像机拍摄下了质子束自调制之后分裂成一长串短质子束的图像.在该实验中, 质子束串激发的等离子体尾波将外注入的能量约18 MeV的电子束加速至近2 GeV的最高能量[15].但是, 美中不足的是, 质子束自调制的过程会持续不断地发展, 特别是由于质子束头部的持续扩散和后退, 最终导致了整个尾波相位的倒退, 从而破坏了质子束串的协同性, 造成了后期尾波电场强度的下降, 同时也使得尾波的相速度下降, 不利于加速带电粒子.这一现象已经被理论和实验所证明[13−16].相关质子束自调制的理论已经被很多文章所阐述[17−21], 这些文章揭示了自调制这一不稳定性过程的增长率、相速度的变化等, 可以说在线性化阶段, 该理论已经发展得相当成熟.

近年来, 随着人们对自调制这一过程研究的深入, 利用种子等离子体尾波控制自调制(seedingself-modulation)的想法逐渐出现在了人们的视线之中.它通过在质子束的前方添加一个激光束或者短电子束, 依靠激光束[18]或者短电子束[22]产生的尾波作为种子来调制质子束, 从而使得整个自调制的过程变得可控.2020年Lotov和Minakov[23]通过理论研究与数值模拟, 发现通过把短电子束种子尾波自调制与等离子体密度梯度相结合, 可以获得一个相对稳定、电场强度又保持在较高水准的尾波.

综上所述, 利用种子等离子体波来控制质子束调制过程具有巨大的潜力, 也是目前AWAKE项目的主要研究方向之一.这方面的研究才进入人们的视线, 对于其机制以及电子束对质子束驱动的尾波相速度的影响目前尚没有被完全认知.由于电子在尾波中加速能量最终取决于尾波的相速度, 因此如何控制尾波相速度、并尽可能提高这个相速度至非常接近真空中光速是个重要研究课题.

本文主要研究以电子束驱动等离子体尾波作为种子的质子束自调制过程, 及其产生等离子体尾波的相速度变化, 并根据模拟结果探讨质子束尾波相速度与电子束的关联.通过二维柱坐标模拟软件LCODE[24], 研究不同电荷密度、能量的短电子束对质子束自调制过程的影响, 特别是质子束尾波相速度的变化, 同时还阐述了短电子束在等离子体中自身的演化对该相速度的影响, 为质子束驱动尾波加速的相关研究提供参考.

2 理论模型与数值模拟

首先介绍关于种子自调制的理论模型.相关的模型前人已经有所研究[19−21], 但是和相应的模拟结果并不一致, 可见相关的理论并不完善.而关于无种子情况下的质子束自调制的理论模型则已经发展得相当完备.在无种子自调制的二维理论模型中, 一束非常长的均匀质子束沿着z方向以vb的速度在均匀等离子体中传输.由于质子束的能量非常大, 可以直接忽略质子在纵向的位移.那么, 可以写出它的包络方程[21]:

方程中ϵn为质子束的归一化发射度,rb为质子束半径,f(ξ) 为质子束的纵向分布√,t为时间,γ为质子的洛伦兹因子,

为等离子体波数,n0为等离子体电子密度, 其中kb=为质子束密度,mp为质子质量, 传播坐标变量ξ=vbt−z≈ct−z,K1和I2则是贝塞尔函数.方程的左边第二项来自于质子束发射度导致的横向膨胀, 而右边第一项则来自于等离子体横向尾波带来的运动趋势.

通过假设kprb≪1 , 同时假定具有一定长度的均匀质子束f(ξ)=1 , 方程(1)可以转变为[21]

其中方程的右边是kprb≪1 情况下的二维粒子束产生的横向尾波分布.可以通过它来引入电子束的横向尾波.这里假设电子束的长度为ξ1, 半径等于质子束的半径(同样符合kprb≪1 ), 密度为Nnb,均匀分布在0—ξ1之间, 这意味着在模型中, 质子束紧跟在电子束的后方, 两者之间的距离为0.另外在该方程中, 假定电子束的分布不随时间演化.把电子束的分布代入方程之后, 就得到了一个新的包络方程:

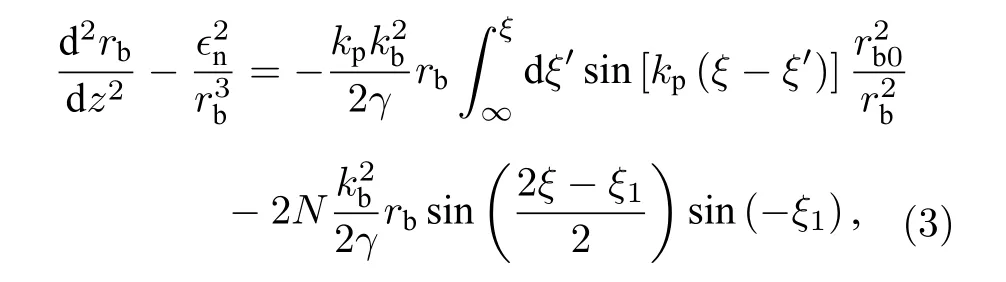
该方程包含了质子束前方电子束的纵向尾波分布.从该方程就可以看出, 电子束产生的横向尾波就是电子束种子自调制与质子束自调制过程之间最大的不同之处.接着对方程(3)做线性化处理[19], 假设 rb≈r0+r1,r0为质子束最终平衡态,r1为质子束自调制期间产生的半径扰动, 并且r1≪r0, 另外假设包络膨胀的速度比较缓慢r1=rˆexp(iξ)+C.C ,及|∂ξrˆ|≪rˆ.这样就得到了简化后关于rˆ 的方程:

由此可知, 当电子束密度非常小时, 种子自调制的整个过程将接近于质子束自调制过程.

通过把质子束半径分布代入等离子体尾波计算公式, 就可以计算出等离子体尾波的强度.再引入文献[19]中的相速度公式

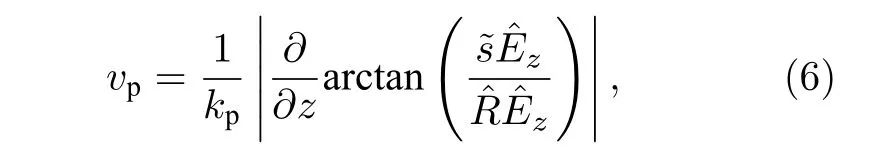
其中为电场的虚部,为电场的实部.通过(6)式, 求解尾波的相速度, 就可以得到存在种子尾波时质子束调制尾波的相速度随时间及空间的分布.

图1为通过上述公式进行数值求解得到的相速度分布.图1中所使用的等离子体密度为n0=7×1014/cm3, 质子束密度为nb=0.0056n0, 均匀分布, 而电子束长度ξ1=1.57c/ωp, 密度为均匀分布.图中分别计算了电子束密度nbe=0nb, 0.25nb,0.5nb, 1nb, 1 0nb, 2 0nb时的质子束自调制过程在ξ = 100时的尾波相速度分布.如图1(a)所示, 在电子束密度非常小的情况下, 种子自调制尾波相速度与无电子束情况下的质子束自调制几乎一致, 相速度仅仅有着极其细微的差距.而从图1(b)则可以看到, 在电子束密度较大时, 整个自调制过程中的尾波相速度随着电子束的密度增大有着明显的提高.并且相速度的最小值也随之微弱地向左移动, 这也表示整个自调制过程随着电子束密度的增加而加快, 电子束具有提高自调制增长率的特性.

图1 在 ξ =100c/ωp 处尾波相速度随时间变化 (a) 电子束密度较低时; (b) 电子束密度较大时Fig.1.Change of the phase velocity with time at ξ =100c/ωp : (a) Low electron beam density; (b) high electron density.

上述的计算使用了一个假设, 由于r0必然是个不为负的实数, 当 1−2Nsin(ξ−ξ1/2)sin(−ξ1) 为一个负数时, 直接假定 1 /r0=0 , 另外, 在N的取值非常大的情况下, 比如N= 40, 此时电子束产生的电场已经处于非线性强度, 而本理论只适用于线性阶段, 所以上述的理论其实对于N有一个适用范围.

接着通过LCODE程序模拟理想状态下, 相同分布、不同电荷量的电子束所引发的种子自调制中不同位置、不同时刻纵向尾波极值的位置变化.LCODE是由Lotov开发的二维柱坐标模拟软件[25],专门用于模拟柱对称粒子束在等离子体中传播所引起的尾波激发和电子加速过程.在模拟中, 选取的模拟窗口长度为 6 00c/ωp, 等离子体的密度为n0=7×1014/cm3且均匀分布, 质子束长度L=1500c/ωp(~3 cm), 半径rb=1c/ωp(~200 µm), 中心能量Eb=400GeV , 中心密度为nb=0.0056n0,纵向密度为均匀分布, 横向为高斯分布.所使用的电子束中心密度为nbe, 纵向均匀分布, 横向为高斯分布, 电子束长度半径rbe=1c/ωp,紧跟在质子束后方, 双方之间没有间隔.这里先考虑一个理想情况, 把电子的能量设置为Ebe=1015GeV , 在能量如此高的情况下, 电子的分布不会随时间演化, 如此就可以与上述的理论进行比较.

图2(b)、图2(d)和图2(f)分别给出了在上述条件下改变电子束的中心密度所模拟出的质子束自调制尾波相速度在时间与空间上的分布.而图2(a)、图2(c)和图2(e)给出了上述条件下质子束自调制尾波电场最大值在时间与空间上的分布.通过对比这些图像可以发现, 随着电子束中心密度的增加,电场最大值峰值出现的时间在整个自调制的过程中越来越早(从无电子束的大约 2 0000c/ωp到nbe=10nb时的大约 1 0000c/ωp), 相对应的尾波相速度变化结构也有着同样的变化, 由此可见, 电子束的引入可以提高自调制的增长率, 压缩整个自调制过程从初始到饱和所需的时间, 并且随着电子束的电荷量的增加, 整个加速的程度愈发明显.

图2 电子束种子自调制模拟结果 (a) 无电子束时的最大电场分布; (b) 无电子束时的相速度分布; (c) 电子束中心密度为1nb时的最大电场分布; (b) 电子束中心密度为 1 nb 时的相速度分布; (e) 电子束中心密度为 1 0nb 时的最大电场分布; (f) 电子束中心密度为 1 0nb 时的相速度分布Fig.2.Results of the simulation: (a) Distribution of Emax when no seeding; (b) distribution of phase velocity when no seeding;(c) distribution of Emax when n be=1nb ; (d) distribution of phase velocity when n be=1nb ; (e) distribution of Emax when nbe=10nb ; (f) distribution of phase velocity when n be=10nb.

图3 (a)给出了在不同电子束条件下尾波的峰值相位变化情况.通过对比图3(a)中的各个曲线的转折点位置, 可以发现所有的曲线都拥有相同的变化规律, 它们的变化趋势也是相同的, 惟一不同的是相速度拐点的位置和相速度的大小.图3(b)和 图3(c)则给出了(ξ=100c/ωp与ξ=300c/ωp处)不同nbe下各处尾波相速度随时间的变化情况.通过对比图3(b)和图3(c)不同nbe情况下的尾波相速度可以发现, 相比于无电子束调制, 在有电子束调制的情况下, 尾波相速度有所提升, 而且尾波的增长率也明显增加了.质子束自调制的增长率随着电子束中心密度nbe的提高而增大, 从而缩短了整个过程的时间, 使得尾波相速度的演化进展加快, 更早地达到了后期相速度接近于光速的稳定状态.这与之前理论推导所给出的结论完全一致, 但是可以发现模拟结果与理论相比在细节上并不一致, 可见想要获得一个精确的关于相速度的分布,数值模拟仍然是不可或缺的.

图3 (a) 不同电子束密度 n be 情况下尾波峰值相位的变化; (b) ξ =100c/ωp 处不同 n be 条件下模拟得到的尾波相速度随时间变化; (c) ξ =300c/ωp 处不同 n be 条件下模拟得到的尾波相速度随时间变化Fig.3.(a) Phase change of the wakefield peak with different electron beam density n be ; (b) evolution of the phase velocity at ξ =100c/ωp with different n be ; (c) evolution of the phase velocity at ξ =300c/ωp with different n be.

图4给出了纵向坐标 0c/ωp—600c/ωp范围的模拟窗口内纵向电场最大值随时间的变化曲线, 从图中的曲线变化可以清晰地看出随着电子束的电荷量提升, 整个自调制过程的增长率(电场增长率)有了明显的提升, 所达到的最大电场也随之提高.

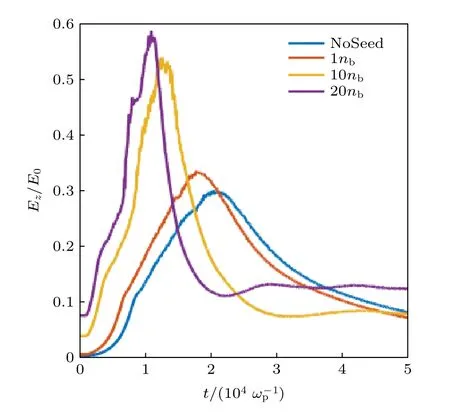
图4 不同电子束密度 n be 情况下最大电场随时间的分布Fig.4.Evolution of the maximum electric field with different electron beam density n be.

综上所述, 电子束可以提升自调制的整个过程的发展速度, 使得整个过程所需的时间缩短, 这也使得尾波相速度的变化幅度加快, 更早地达到了后期相速度接近于光速的稳定状态, 有利于后续的电子加速.

3 电子束参数对尾波相速度的影响

上一节讨论了理想状态下电子束种子尾波对质子束自调制过程中尾波相速度的影响, 所采用的电子束能量极高, 使其在传输过程中不发生变化,是一种简化后的模型.然而在实际的情况中, 电子束的能量不可能如此之高, 相应地, 电子束在等离子体传播的过程中, 它的密度分布、形状、能量都会发生变化.这些改变也会影响尾波相速度.本节考虑了有限能量电子束传输过程的演化对尾波相速度的影响.

首先介绍理论计算.当电子束在等离子体中传播时, 它会受到一个来自等离子体的径向的作用力以及本身的库仑排斥力, 其横向尺度满足[17]

其中τ=t为传播时间,I1和K1为修正贝塞尔函数.假如电子束的发射度非常小, 那么电子束将受到一个径向压缩的作用力, 进入一个自聚焦的过程.在这个过程中, 电子束的半径在不断地变小,密度在不断地变高, 从而它所激发的电场也在不停地变强.

假设粒子束的平衡态满足如下条件:

并且粒子束的头部满足真空中发射度自由膨胀方程[17]

可以利用方程(8)和方程(9)来求解出不同时刻粒子束的平衡态.

图5(a)和图5(b)给出了通过(8)式和(9)式计算的一束长度半径r=1c/ωp, 发射度εe=3×10−4rad/mm , 能量为Ebe的电子束刚进入等离子体中时的平衡态分布.可以看到电子束的半径, 特别是后半部分, 有一个非常明显的压缩.由此可见, 在等离子体中传播的初期, 电子束将经历一个极其显著的压缩过程, 而压缩后产生的高密度也自然使得其产生的电场有了巨大的提升, 从而改变了整个尾波的分布.

图5 (a) 电子束能量 E be=100MeV 时不同电子束密度nbe的平衡态分布; (b) n be=10nb 时不同电子束能量Ebe 的平衡态分布Fig.5.(a) Equilibrium configuration with different electron beam density n be when Ebe =100 MeV; (b) equilibrium configuration with different E when n be=10nb.

图6给出了根据(7)式—(9)式计算所得的存在电子束种子时, 质子束自调制过程中的平衡态密度分布.计算过程中所使用的参数如下: 等离子体密度n0, 电子束初始密度nbe=5nb, 均匀分布, 电子束能量Ebe= 100 MeV, 发射度εe=3×10−4rad/mm , 长度ξ1=1.57c/ωp, 初始半径rbe=c/ωp; 质子束密度nb=0.0056n0, 纵向无限长且均匀分布, 中心能量为Eb= 400 GeV, 发射度εp=3×10−4rad/mm , 初始半径rb=c/ωp.该计算中采用了两个假设: 1)忽略电子束半径分布的变化, 即rbe(ξ,t)=rbe(t); 2)忽略电子束的能量衰减.首先, 通过上述假设和方程(7)求得电子束在某一时刻下的半径; 其次, 将电子束分布和质子束参数代入方程(7), 从而求得在该时刻电子束后方的质子束平衡态密度分布, 最后再通过n(ξ,t)=计算出该时刻各个纵向位置的平衡态密度分布.图6中选取了三个时刻(t=0 ,410/ωp, 5 89/ωp), 分别对应着电子束半径rbe=c/ωP, 0.75c/ωP, 0.5c/ωP三种情况, 展示了电子束(0至虚线范围内)后方质子束的平衡态密度分布的变化图像.通过对比不同时刻的质子束平衡态密度分布, 可以得知当电子束处于被压缩状态时(可以看到电子束的密度越来越高), 质子束的包络会有向前运动的趋势, 那么相应质子束产生的尾波相位也会存在向前运动的趋势, 这也是形成超光速尾波相速度的主要原因.总之, 当电子束处于自聚焦状态时, 可以得到一个超光速的尾波相速度.

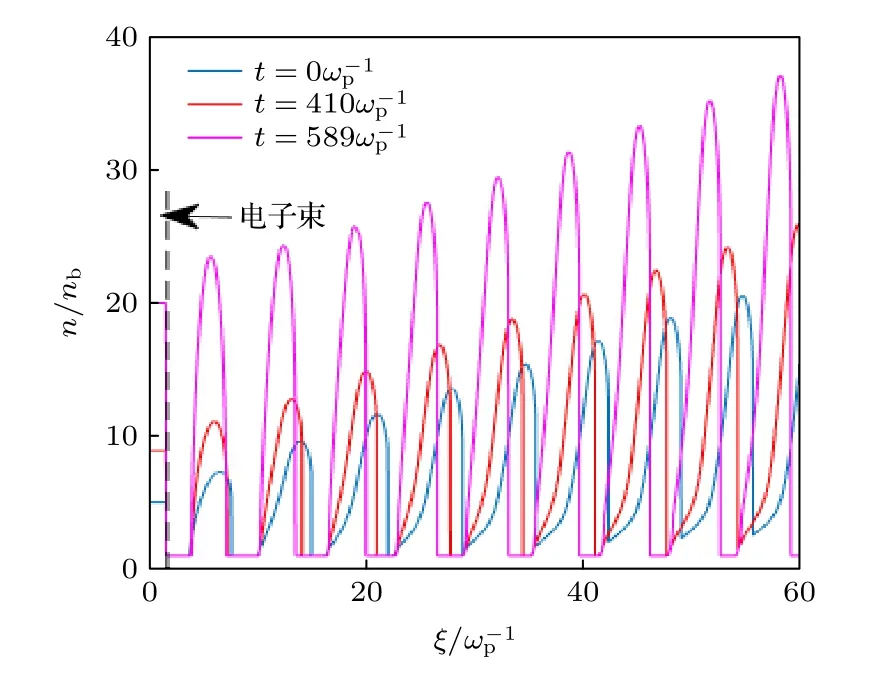
图6 电子束压缩引起的质子束平衡态变化, 即在三个时刻的质子束平衡态分布Fig.6.Equilibrium configuration of proton beam with a compressing electron beam.

接下来的模拟是基于之前的等离子体和质子束参数, 考虑了相同电子束分布和电荷量, 但不同能量的模拟参数对尾波相速度的影响.在模拟中,等离子体的密度为n0=7×1014/cm3且均匀分布,质子束中心能量Eb=400GeV , 长度L=1500c/ωp(大约3 cm), 半径r=1c/ωp(大约200 µm), 中心密度为nbm=0.0056n0, 纵向分布为均匀分布, 横向为高斯分布.所使用的电子束长度半径r=1c/ωp,电子束中心密度nbem=10nb,纵向分布为均匀分布, 横向为高斯分布, 电子束中心能量总共选取了三种, 分别是Ebe= 100 MeV,500 MeV, 1 GeV.

图7 (a)—图7(c)给出了在上述条件下改变电子束的能量(100 MeV, 500 MeV, 1 GeV)所得到的质子束自调制尾波电场最大值在时间与空间上的分布.图7(d)€—图7(f)则给出了上述条件下质子束自调制尾波相速度在时间与空间上的分布.图8(a)和图8(b)则是挑选了ξ=100c/ωp与ξ=300c/ωp的位置, 不同能量的电子束所得到的尾波相速度进行比较.可以发现, 在自调制初始的时期,出现了相速度大于光速的现象, 这与之前提到的电子束自聚焦理论相符合.能量越高, 该现象就越不明显.另外通过对比图7和图8中的数据, 可以发现对自聚焦起到关键作用的有两个参数, 即电子束的能量和密度.如果电子束的能量γ过高, 那么它受到的径向加速度也随之减弱, 如图8(a)和图8(b)所示, 自聚焦对相速度的影响程度随着能量的增高而渐渐减弱.而如果增强电子束的密度, 则自聚焦的速度就会明显加快, 整个自聚焦的过程所引发的超光速相速度也会愈发明显.

图7 利用电子束种子尾波调制质子束的模拟结果 (a), (b), (c)分别对应电子束能量 E be = 100 MeV, 500 MeV, 1 GeV时的最大电场随时间变化; (d), (e), (f) 分别对应电子束能量 E be = 100 MeV, 500 MeV, 1 GeV时的相速度随时间变化Fig.7.Simulation of proton beam modulation with electron beam seeding:(a), (b), (c) The maximum electric fields as a function of time for the electron beam energy at E be=100MeV , 500 MeV, and 1 GeV, respectively; (d), (e), (f) the phase velocity as a function of time for the electron beam energy at E be=100MeV , 500 MeV, and 1 GeV, respectively.

图8 (a) 在 ξ =100c/ωp 处不同电子束能量模拟得到的尾波相速度随时间变化; (b) 在 ξ =300c/ωp 处不同电子束能量模拟得到的尾波相速度随时间变化Fig.8.(a) Phase velocity as a function of time at ξ =100c/ωp for different electron energy; (b) phase velocity as a function of time at ξ =300c/ωp for different electron energy.

另外, 电子束在尾波中传播时还受到了一个纵向的电磁力[25]:

而与之相对的, 电子束作为尾波的能量来源, 它每时每刻减少的能量正好与之产生的尾波强度相对应, 可以得出电磁力F正比于电子束密度nbe, 这也意味着, 电子束的能量耗散速度正比于电子束所携带的电荷量.当电子束的能量衰退, 其发射度所引起的膨胀效应会超过尾波引起的压缩效应, 这个时候, 电子束就会膨胀, 它的密度降低, 从而产生了与上述自聚焦过程相反的现象, 使得相速度有所降低.不过, 假如电子束有着足够的能量,那么这个过程就会发生的比较缓慢.另外, 当电子束的能量耗尽时, 它会在纵向上变形分裂, 从而产生不稳定的相速度, 如图8(a)和8(b)所示.同理,如果降低电子束的电荷量, 那么也自然可以减缓该过程.

当等离子体尾波中的电场增加到接近于E0时, 由于相对论非线性效应, 等离子体中尾波的波长就会被拉长[26], 可以近似描述为λP=λp0[1+α(Em/E0)2], 其中λp0为线性理论中的等离子体波长,α是一个参数.假定整个长质子束所形成的尾波结构在纵向上包含了N个波长, 那么当每一个波长都被拉长一点点时, 对于尾波的相位,特别是距离质子束头部较远的位置, 具有极大的影响.一般而言, 无论是质子束自调制还是电子束种子尾波诱导调制, 它们的尾波大致变化都是先上升后下降的, 而它们产生的尾波所能达到的最大电场大致在0.4E0—0.7E0.当一个位置的电场从E1变化到E2时, 根据上述λP公式, 它的波长变化及相位变化大约为

所以, 当尾波在快速增大时, 该非线性效应会使得尾波的相速度发生巨大的下降, 并且随着ξ(N)的增大而愈发明显; 当尾波在快速下降时, 尾波的相速度会快速地上升, 甚至于突破光速, 产生超光速的相速度.然而该过程是非线性效应, 很难被精确描述, 只能根据公式定性描述出大致的物理图像.该机制在没有种子电子束尾波存在的质子束自调制过程中也会对尾波相速度的演化起到相当重要的作用.

4 质子束纵向密度分布对尾波相速度的影响

现今AWAKE实验[15]中所使用的模型并不是如以上所述的在纵向上完全均匀分布, 而是余弦函数的半波型, 函数表述为其 中nbm=0.0056n0为中心密度,σr=1c/ωP, 它是一个纵向密度从0开始上升并最终回到0的这样一种分布.该实验利用激光束产生的移动等离子体边界来对质子束产生调制.在没有电子束的情况下, 这样的过程非常不利于质子束的自调制, 因为不仅增长率缓慢,而且极易激发软管不稳定性[14], 不利于后续粒子束的加速.而在现有的电子束种子调制方案[22]中,电子束的引入将使得原本处于激光束前半段的质子束也可以运用于尾波加速的整个过程, 从而避免不必要的浪费.在该方案中电子束引入所带来的变化和上述移动等离子体边界引起自调制的过程有很大区别.

在引入上述的质子束分布的情况下, 比较了没有电子束与引入电子束的情况.在有电子束的模拟中, 电子束的参数如下: 能量E= 100 MeV,长度ξ1=1.57c/ωp,σre=1c/ωp, 中心密度nbem=0.0056n0, 电子束的空间分布表述为nbe(r,ξ)=即纵向分布为余弦函数半波型, 横向分布为高斯分布.

图9(a)和图9(b)分别对比了ξ=500c/ωp,ξ=750c/ωp两个坐标下无种子尾波的自调制与有种子尾波调制情况下质子束尾波相速度随时间的变化情况.可以明显地看出有电子束的情况下, 尾波相速度尤其是在模拟后期有了明显的增加.另外, 由于电子束的电荷量比较低, 在等离子体中的能量衰减速度比不上图8中100 MeV所对应的模拟, 故而图9中并没有图8后期出现的不稳定相速度, 这与上一节所阐述的结论是一致的.综上所述, 即便改变了质子束的分布, 电子束依然可以提高平均相速度, 之前所得到的结论在改变质子束分布的情况下也依然适用.

图9 (a) 在 ξ =500c/ωp 处模拟得到的尾波相速度随时间变化; (b) 在 ξ =750c/ωp 处模拟得到的尾波相速度随时间变化Fig.9.(a) Phase velocity as a function of time at ξ=500c/ωp ; (b) phase velocity at ξ =750c/ωp.

5 结 论

本文通过理论分析并利用二维柱坐标模拟软件LCODE研究了电子束的种子尾波对质子束自调制尾波相速度的影响.发现电子束可以提升整个质子束自调制的增长率, 提升尾波相速度, 并且电子束的电荷量越高, 提升的效果越突出.另外研究还发现, 电子束在质子束自调制过程的前期会通过自聚焦的效应提升相速度.电子束的电荷量越高、能量越低则相速度提升愈发明显; 通过选取合适的参数, 甚至可以获得一个超光速的相速度.此外,本文还探讨了诸如电子束能量耗散、相对论效应引起的等离子体波长拉长等效应对相速度的影响, 并在最后比较了不同质子束分布情况下相速度的演化, 验证了上述电子束种子尾波对质子束自调制尾波的相速度影响的相关结论适用于不同质子束密度分布.本研究对于未来的电子束种子自调制尾波加速方案具有一定的参考价值.

作者感谢俄罗斯Budker核物理研究所Konstantin Lotov教授允许使用他开发的LCODE程序, 并提供相关帮助.