强散射过程与双随机相位加密过程的等价性分析*

陈洁 周昕 白星 李聪 徐昭 倪洋

(四川大学电子信息学院, 成都 610065)

薄层强散射介质的散射系统只会引起入射光波的振幅和相位分布变化, 但不会导致总能量的衰减.这一过程可以看成光波被散射系统编码的过程, 与双随机加密系统极为相似.本文首先证明了载有目标信息的光波在通过薄层强散射介质的散射系统时所产生散斑的分布特性, 与双随机加密系统加密同一明文目标所得到的密文分布特性具有高度的相似性.然后, 本文将该散射系统视为一个双随机加密系统, 并利用相位恢复算法精确地计算出该散射系统所对应的两块随机相位密钥, 同时证明了这两块密钥板还可以成功地从该散射系统所得到的其他任何散斑中恢复出对应的原始图像.最后, 为了进一步证明二者的等价性, 本文使用一种适用于双随机加密系统的唯密文攻击方法, 成功地破解了薄层强散射介质的散射系统, 得到了较好结果.

1 引 言

近年来, 采用非侵入、直接的成像方式透过散射介质恢复出目标的原始结构和信息, 在光学成像领域已成为备受瞩目的研究热点, 特别在医学诊断、军事安全、纳米技术应用及水下探测等方面显得极为重要和迫切[1−4].对于微粒尺寸为波长量级且空间分布随机的介质, 入射光在其内部传播时会产生强烈的散射, 从而导致原本有序的波前相位发生严重畸变[5].这些强散射光会在观测表面随机分布, 产生相长干涉和相消干涉, 最终形成散斑图.当散射介质厚度较小时, 对入射光总能量的影响可以忽略不计.最近, 一些研究成功地实现了从薄层强散射介质出射光场中重建出隐藏的目标图像[6−8].如: 基于相位多样性的成像方法, 通过采集多帧散斑, 并结合相位分集重建算法进行联合重建[5]; 基于双谱分析的单帧散斑成像方法, 通过分析散斑的双谱信息来提取目标的相位信息[6]; 将波前相位调制技术[8]和菲涅耳衍射理论[7]相结合,实现了强散射介质中的聚焦; 还有强散射介质传输矩阵的测量, 也对散斑图样恢复具有重要意义[9−11],包括三步相移干涉法[9]和任意步相移干涉法[10],以及通过结合光声效应实现不受光记忆效应限制的光声传输矩阵[11]的测量.

当入射光透过强散射介质时, 虽然从杂乱无序的散斑图不能直接获得成像目标的信息[12], 但事实上入射光所携带的信息只是由于散射而变得无序, 却并没有丢失.也就是说, 入射光波信息被散射介质系统所编码, 表现为杂乱无序的出射光场状态.由于粒子在散射介质中的随机分布不随时间变化, 一旦给定了随机散射介质, 同一入射光通过相同介质的出射场是相同的.因此, 如果能够对散斑图像进行解码, 则可以有效恢复出目标物体.通过数值模拟我们发现, 对于同一幅给定的目标图像,在光学记忆效应范围[13]内的强散射介质[14]散斑图样和双随机加密(DRPE)系统的密文图样在统计分布上具有相同的分布规律.在此基础上, 我们将散射系统与DRPE系统联系起来, 把这样的强散射介质视为DRPE编码系统.将原始目标作为空间约束条件, 散斑图样作为频域约束条件, 迭代进入相位恢复算法中得到散射系统的两个随机相位密钥, 并且这一对密钥还可以成功解密经过同一散射系统中的其他散斑图像.受到成像相关技术[15]和DRPE系统唯密文攻击方法[16]的启发,我们还对散斑图案执行了DRPE加密系统的“唯密文攻击”方法(COA).随着散斑图样实现次数的增加, 计算得到散斑的傅里叶域强度平均自相关值会越来越收敛到目标物体的能量谱密度(ESD)[15].然后, 将得到的ESD近似值输入相位恢复算法[17]中进行迭代运算, 便对散斑图案进行了成功解码,恢复出原始目标信息.理论上, 所有适用于双随机相位加密系统的唯密文攻击方法都适用于此种散射介质散斑图像的恢复.

本文第一次验证了薄层强散射系统与DRPE系统的等价性, 基于这一特性, 可以利用DRPE系统解密的方法来解决散射介质成像的许多问题, 这为非侵入式透过散射介质成像提供了新的思路.

2 基 础

2.1 散射成像系统

散射成像系统如图1所示, 物体被相干光照射, 散射介质被放置在目标物体和成像平面之间.对于文献[5]中提出的强散射介质薄层, 我们假设散射介质引起的入射光振幅损失可以忽略.在光学记忆效应范围内, 可以将散斑写成目标物体和成像系统的点扩散函数的卷积[12]:

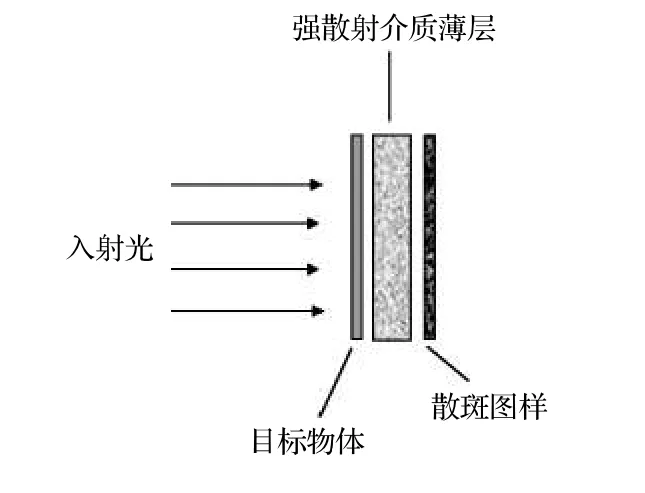
图1 散射过程Fig.1.Scattering process.

其中,S(x,y) 是光学记忆效应范围内散射系统的点扩散函数.

散射介质出射的光场可以表示为[5]

其中, (x,y) 表示二维空间坐标,|A(x,y)|代表散射光场的振幅, e xp[iθ(x,y)] 则代表散射光场的相位.散斑图案的强度信息可表示为

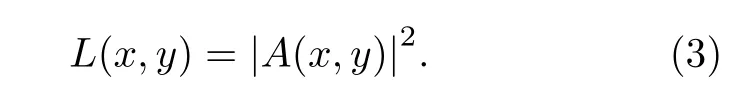
散射光场A(x,y) 的实部和虚部都近似分布为高斯随机变量, 其均值都为零; 散射光场的模值|A(x,y)|服从瑞利概率密度分布[18]:

其中,a表示散斑模值|A(x,y)|,σ2表示散射光场实部和虚部的方差.散射光强度服从负指数统计分布[19]:

其中表示光强的平均值.

2.2 DRPE系统

经典的双随机相位加密系统由标准的4f系统实现, 如图2所示.输入图像f(x,y) 在空域受到第一块随机相位板 e xp[i2πn(x,y)] 的调制作用, 经过第一块透镜的傅里叶变换后, 在频域受到第二块随机相位板 e xp[i2πb(u,v)] 的调制作用, 再经过第二块透镜的傅里叶变换作用, 在输出平面上可得到密文图像[20]:

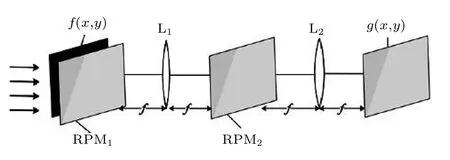
图2 双随机相位加密系统Fig.2.Double random phase encryption system.

其中, (x,y) 和 (u,v) 分别表示二维空域坐标和二维频域坐标,n(x,y) 和b(u,v) 代表以均匀概率在区间[0, 1]上随机取值的任意实数, Γ 和 Γ−1分别表示傅里叶变换和逆变换.

3 等价性分析

3.1 散射系统与DRPE系统的统计分布规律

我们用一幅原始图像E作为目标物体, 分别经过薄层强散射系统和DRPE系统后, 所得到的散斑图案和密文图样灰度直方图统计分布(图3)的散斑和密文的统计分布规律是一致的, 原始图像E如图4(a)所示.其中, 散斑图案和DRPE系统密文的实部和虚部都近似为独立分布的高斯随机变量, 模值均服从瑞利概率密度分布, 而光强则均服从负指数概率密度分布.对于其他任意的同一原始图像, 都可以得到与图3类似的结果.基于此,我们认为, 薄层介质强散射过程与DRPE加密系统具有高度的相似性.在本文中, 我们考虑的等价性是指薄层强散射系统和DRPE系统性能的等价性, 即两个系统从各自的入射面到出射面所产生结果的等价, 也就是说, 介质到探测器的距离是在我们所说等价的两个系统之外的光场衍射过程.显然, 讨论中最简单的情况是当这个衍射距离为零时, 也就是探测器刚刚放在散射介质的出射面处.当然这样处理也是只具有理论讨论意义, 忽略了实际的情况下散射介质物理尺寸和探测距离的影响.

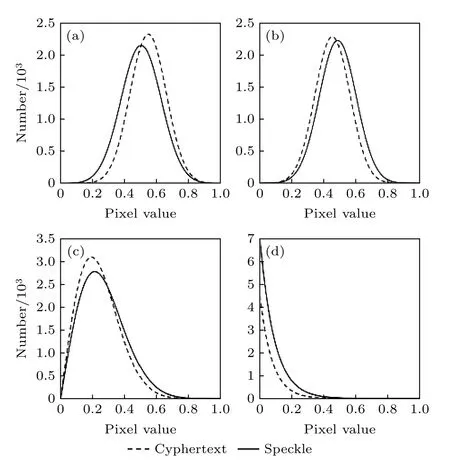
图3 散斑和密文的统计直方图 (a)实部; (b)虚部;(c)振幅; (d)强度Fig.3.Statistical distribution histogram of speckle and cyphertext: (a) Real part; (b) imaginary part; (c) amplitude (d) intensity.

3.2 散射系统的一对密钥

在经典的DRPE系统中, 两个随机相位板分别在空间域和频率域对输入图像进行调制, 使密文成为平稳的白噪声.而对于强散射介质薄层, 也可以认为散射介质主要影响入射光的相位而引起光场分布的改变[21].因此假设图1所示的强散射过程等效于图2中所示的DRPE系统, 则该散射过程应具有两个相应的密钥板, 利用相位恢复算法模拟就可以找到这两个相位密钥.

根据文献[5]提出的强散射效应薄层介质模型, 在光学记忆效应范围内, 散斑场是具有空间平移不变性的[21], 因此由(1)式可以得到如图4(b)所示的散斑图样.对散斑A(x,y) 进行变换可得到[22]:

其中,φ(u,v)=Γ{O(x,y)·exp[i2πn(x,y)]},n(x,y)和b(u,v) 为在[0, 1] 区间随机取值的任意实数.这样,根据物体平面上的强度信息|φ(x,y)|=O(x,y) 和傅里叶平面上的强度信息|φ(u,v)|=|Γ{A(x,y)}|,利用Gerchberg-Saxton(GS)相位恢复算法[17]迭代就得到第一个随机相位密钥, 即目标平面上的密钥n(x,y).而第二个随机相位密钥, 即频谱平面的随机相位板b(u,v) 可由目标平面的密钥推导出[22]:

至此, 我们已经成功地找到了散射系统的一对密钥, 并可以用这两个密钥解密经过同一散射介质的其他散斑图样.相应过程的数值模拟结果如下: 图4(c)为通过迭代获得的第一块密钥板分布,图4(d)则为由(8)式得到第二块密钥板的随机相位函数分布.而用这一对密钥可以对经过同一散射系统的另一幅散斑图像进行解密, 其对应的原始图像为图4(e), 解密图像如图4(f)所示.

图4 (a)原始图像; (b) 经过强散射薄层后的散斑; (c)第一块密钥板; (d)第二块密钥板;(e)另一原始图像; (f)利用两块密钥板解密出的图像Fig.4.(a) Original image;(b) speckle suffered highly thin scatter layer; (c) first encryption key; (d) second encryption key; (e) another original image; (f) decrypted image by two keys.

在我们的迭代模拟中, 两块随机相位板都以均匀概率在[0, 1]之间选取初始值.解密出来的两块随机相位板的统计分布直方图如图5所示, 从直方图来看, 第二块随机相位板比第一块更接近满足均匀概率分布, 它们的方差分别为3.2705和3.3093.由于第一块相位板有两个突出的峰值, 这意味着本文示例中相位迭代运算所最终确定的第一块相位板, 其相位分布概率已不再是完全理想的均匀概率分布情况.

图5 (a)第一块随机相位板统计分布直方图;(b)第二块随机相位板统计分布直方图Fig.5.(a) The histogram of first random phase key; (b) the histogram of second random phase key.

4 讨 论

由于经典的DRPE技术存在受到唯密文攻击的可能性[17], 基于二者的等价性, 我们认为对散射介质形成的散斑图案进行相同的唯密文攻击来恢复目标图像也是可行的.当散射介质和CCD分别位于透镜的前焦面和后焦面时, CCD接收到的信息为傅里叶域强度图样, 可以写成:

其中,P(u,v) 表示的是总孔径函数,∆Sn(u,v)=Sn(u,v)−〈Sn(u,v)〉 ,nth是自相关函数Sn(u,v) 的系综平均实现次数,是目标物体的ESD值.

为了能够直接探测到散斑的傅里叶域强度图样, 设计的散射成像系统装置如图6所示.其中d表示物体与散射介质层之间的距离,f表示透镜的焦距.随着散斑实现次数N的增加, 散斑傅里叶域强度Sn(u,v) 的自相关平均值会收敛到目标对象的ESD值:

图6 散射成像系统示意图Fig.6.Schematic diagram of scattering imaging system.

显然, (10)式表明, 只要实现足够数量的散斑,就可以提取出目标物体的ESD值, 其中包含了目标物体的全部信息.ESD值的平方根即是物体强度傅里叶变换模值的估计.使用相位恢复算法[17],可以从目标物体的傅里叶变换模值中恢复出目标物体的强度值.

在我们的模拟中, 原始图像是文本为E的二值图像, 其大小为256 × 256像素, 如图7(a)所示.在光学记忆效应范围内, 由(3)式可得到散斑.对散斑进行傅里叶逆变换后, 取结果的平方, 得到由(10)式描述的散斑强度图案Sn(u,v) , 如图7(b)所示.由于能量谱密度集中在图像的中间, 因此取散斑图在时间上的平均值而不是在空间上的平均值.我们的模拟采用了N=104个散斑强度图样.接着计算得到每个散斑强度图案的自相关, 取其平均值, 根据(10)式生成目标物体的ESD的估计值,如图7(c)所示.物体强度的傅里叶变换模值通过求ESD的平方根得到, 然后将估计的傅里叶变换模值输入相位恢复算法[17], 得到图7(d)所示的重建明文图像.

图7 (a)目标物体; (b)傅里叶域散斑强度; (c)ESD的估计值; (d)恢复出的目标图像Fig.7.(a) Original plaintext image; (b) Fourier-domain speckle intensity;(c) estimated ESD; (d) recovered plaintext image.

为了实现这种恢复方法, 散斑实现的次数N应尽可能多, 反馈到相位恢复算法中进行迭代的能量谱更集中, 可以获得更好的可恢复性.这里我们选择了结构相似性(SSIM)作为重建效果的评价标准.结构相似性计算公式为

其中:ux和uy分别表示图 像x和y的平均值;σx和σy分别表示图像x和y的标准差;σx2和σy2分别表示图像x和y的方差;σxy表示图像x和y的协方差;C1和C2都是常数, 为了避免零分母, 通常取C1=(K1×L)2,C2=(K2×L)2,K1=0.01 ,K2=0.03 ,L=255(L为像素值的动态范围).根据上述公式计算得出, 重建图像与原始图像之间的SSIM为0.8520.

这种“散斑的唯密文攻击”方法相当于实现了透过散射介质的非侵入式成像, 可以直接从CCD接收到的强度图中恢复出原始物体图像.这是依据当散斑实现的次数足够多时, 原物体和散斑的能量谱密度相等的原理来完成的.当然, 这种方法也存在着一些不足, 正如图7(d)所示的那样, 由于算法中的平均过程, 使图像的许多细节被平均化, 从而降低了重建图像的质量.

5 结 论

综上所述, 本文通过数值模拟方法验证了强散射系统和双随机编码系统是等价的, 并且受图像相关性的启发, 提供了一种简单有效的利用唯密文攻击从薄层强散射系统散斑中恢复目标图像的方法.数值模拟结果表明: 通过对多次实现的散斑强度数据进行平均, 可以估计出目标物体的傅里叶模值;然后, 根据傅里叶模值的估计, 应用具有非负约束的相位恢复算法就可以重建原始图像.该方法完全可以推广到传统实现散射介质的光谱成像中去.

不过, 需要特别指出的是, 由于透过散射介质成像是一个极其复杂的过程, 因此本文实际上对相应过程进行了理想简化处理.本文中的强散射体是指表面高度随机起伏的标准偏差大于照明光波波长的散射体, 此时散射光波的初始位相均匀地分布在区间(−π,π )上[14].而薄层则为了强调散射介质对振幅的影响较小, 即只改变相位.这种散射介质模型在前人的文献中也有使用[13,21], 相应的实物有毛玻璃, 厚度为380 µm的鸡胸肉, 80 µm的葱表皮[13]等.本文所描述的等价系统是指从散射介质的入射面到出射面与DRPE系统的入射面到出射面等价.然而, 在实际过程中仍然存在着从物体到入射面和出射面到接收面的衍射过程, 这两个衍射过程会导致散射介质的入射图像和出射图像出现一定的衍射效应.在实际处理加解密过程时, 需要把这两个衍射过程的影响考虑进去, 但在本文中为了简化表述, 将物体面、散射介质和观察面设计为紧靠在一起.我们认为, 在理想条件下, 由于薄层强散射系统和DRPE系统的等价性, 理论上所有适用于DRPE系统的纯密文攻击方法, 都可以应用于薄层强散射系统的散斑恢复, 因此今后有可能发展出更多利用系统等价性破解散射光场的方法.