基于UPSO-Kriging的综采工作面三维建模研究

张小艳，许慧，姜水军

(1.西安科技大学 计算机科学与技术学院，陕西 西安 710600; 2.中国神华神东煤炭集团，陕西 榆林 719315)

0 引言

近年来，随着数字矿山概念的提出，三维地质建模在行业领域中备受关注。因此，对综采工作面煤炭赋存形态空间三维可视化成为煤炭生产管理过程中的一个重要环节。

目前三维地质建模在行业领域中备受关注。范文瑶等[1]基于GOCAD软件对研究区域进行三维建模与可视化操作；尚福华等[2]为了解决传统三维地质模型中不能有效地分析地层和断层之间的形态和结构，构建出了一种TIN-Octree混合空间数据模型的精确三维地质结构方法；宋越等[3]将研究的重点放在了解决边界不连续的问题层面上，提出了一种基于机器学习的扩展纹理样本库的方法。

空间数据插值是三维建模过程中的一个至关重要的环节。自20世纪初以来，就有大量的学者对此展开研究并取得了卓越的成效。Kriging算法被广泛用于各类观测的空间插值。本文提出了一种用自适应PSO算法优化Kriging插值算法(UPSO-Kriging)，将其用于工作面煤层高程值预测，为绘制工作面煤层赋存形态三维图提供基础数据，并以神东集团大柳塔煤矿604工作面的实际数据验证了算法的可行性,进而基于规则网格法构建DEM数字高程模型，以Three.js为平台实现了浏览器端综采工作面三维可视化，为煤炭企业开采提供科学依据。

1 Kriging插值法

Kriging插值法是一种基于协方差函数对空间随机过程建模和预测的回归算法[4]。一般公式可表示为：

(1)

式中:待测样本点的值为Z*(x)，已知样本点的值以及个数分别为Z(xi)、n，第i个已知样本点相对于未知样本点的权重为λi[5]。

当Lagrange乘数法求取的最小估计方差满足本征假设时，用变差函数表示Kriging方程组如式(2)所示：

(2)

式中：μ为Lagrange系数，γ(xi,xj)为两个已知采样点xi,xj的变差函数值。

2 UPSO-Kriging插值法

变差函数模型拟合中的参数确定是Kriging插值过程中的关键所在[6-7]。本文针对传统Kriging插值法在变差函数模型拟合中存在的过拟合或欠拟合而导致算法整体精度下降的问题，提出一种自适应PSO算法来优化模型中的3个参数，提高算法整体预测精度。

2.1 自适应PSO算法

2.1.1 PSO算法

粒子群优化算法(PSO)是目前广泛运用于各个领域的进化算法[8]，具有简单、准确、收敛速度快等特点。标准PSO算法更新公式如下[9]：

c2r2[pg(t)-xi(t)],

(3)

xi(t+1)=xi(t)+vi(t+1),

(4)

2.1.2 UPSO算法

针对PSO算法存在的搜索时间过长、易陷入局部极值的最优化等问题[13]，本文采用张小艳等[14]提出的优化方法。分别对算法寻优过程中的粒子位置更新方式、迭代预选值处理以及基于正态分布的惯性调整策略进行优化。

为验证UPSO算法的有效性，本文分别选取4个函数作为标准测试函数，与PSO算法在python2.7环境下进行仿真测试。其中包括两个单峰函数：Sphere函数与Schwefel函数；两个多峰函数：Ackley函数与Rastrigrin函数。单峰函数用来测试算法的收敛速度以检验其局部搜索能力，多峰函数用来检验算法的全局搜索能力从而衡量算法综合性能。

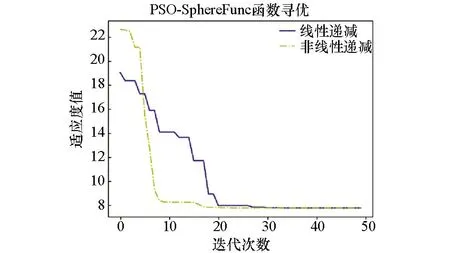
图1 Sphere函数收敛测试Fig.1 Sphere function convergence test diagram

图2 Schwefel函数收敛测试Fig.2 Schwefel function convergence test diagram

图3 Ackley函数收敛测试Fig.3 Ackley function convergence test diagram

图4 Rastrigrin函数收敛测试Fig.4 Rastrigrin function convergence test diagram

由上图可知，不管是在单峰测试函数下的局部搜索能力还是多峰函数下的全局搜索能力，UPSO算法相比PSO算法来说,得到最优解的收敛速度更快，陷入局部极值的次数明显少于原始算法。这均表明UPSO算法整体性能得到了提升。

2.2 UPSO-Kriging插值法

UPSO算法优化Kriging插值法，主要通过UPSO算法迭代寻优得到最优的模型参数进行变异函数模型的拟合，进而得到预测结果。算法步骤如下:

1)确定待求解问题的参数与目标函数。以变差函数模型中的3个模型参数作为求解参数，即块金值c0，偏基台值c，变程a，目标函数为不同距离下的实验与理论变差函数差值平方和[15],即

(5)

2)初始化粒子群。设群体规模为M，将3个模型参数作为一个粒子个体，即xi=(c0,c,a),i=1,2,…,M。种群中每个个体的参数初始化取值如下：

(6)

其中，Rmax是实验变差函数的最大值，Amax为最大滞后距[16]。

3)确定UPSO算法的有关运行参数。其中包括惯性权重最大最小取值vmax,vmin;学习因子最大最小取值c1s,c1f,c2s,c2f；迭代次数Iter；速度vmax,vmin；位置xmax,xmin。

4)UPSO优化运算。优化过程中，通过目标函数来评价群体中每个个体的适合度值是否达到标准，通过更新迭代过程中的速度和位置进行迭代寻优运算。若当前迭代中的最优解不满足终止条件则继续;若满足，则停止。最终结果即最优变差函数参数，由此可拟合出相应的变差函数表达式。

5)Kriging插值预测。将最终得到的变差函数代入式(2)即可得到权重系数，再通过式(1)计算出待预测点的属性值。

3 实验验证

3.1 数据准备

本文运用神东集团大柳塔煤矿604综采工作面，宽度300 m，深度3 400 m，煤层厚度在6.24～40.17 m的69组煤层煤样数据作为样本数据集，验证UPSO-Kriging算法应用于综采工作面煤层高程属性预测的可行性。部分样本数据如表1所示。

表1 采样点数据

3.2 基于UPSO-Kriging的高程值预测

基于样本数据集合中同一煤层下的数据，分别优化UPSO-Kriging插值中的球面、指数以及高斯模型，并与PSO-Kriging以及Kriging的插值预测效果进行比较，其中PSO算法相关参数设置如表2所示。变差函数模型参数的边界区间如表3所示。

表2 PSO算法的参数设置

表3 变差参数的边界设置

将实际采样点高程与预测点之间的均方根误差(RMSE)和平均绝对百分误差(MAE)作为算法评价指标进行分析，其中MAE和RMSE公式分别为：

(7)

(8)

由表4可知，在UPSO-Kriging插值方法下将指数模型作为变差函数理论模型时，效果最佳。结合69组初始样本点数据绘制高程值分布折线A；然后分别根据UPSO-Kriging算法、PSO-Kriging算法计算出待预测点的高程值，绘制出相应高程预测折线B及折线C，最终实验对比图如图5所示。

由表4和图5可以看出， UPSO-Kriging算法在各种评价指标下插值的结果都优于其他算法。因此，基于UPSO-Kriging算法的工作面煤层高程值预测完全可行。

表4 估算精度比较

图5 采样点高程分布对比实验Fig.5 Broken line diagram of elevation distribution of sampling points

4 工作面煤层三维模型

4.1 基于规则网格的DEM模型建立

数字高程模型是利用有限的地形数据对地形进行数值模拟，通常分为规则网格DEM模型、TIN模型、等高线模型等[17]。本文结合煤层实际地形特点，基于matlab仿真实现的单层DEM高程模型以及多层DEM高程模型分别如图6,7所示。

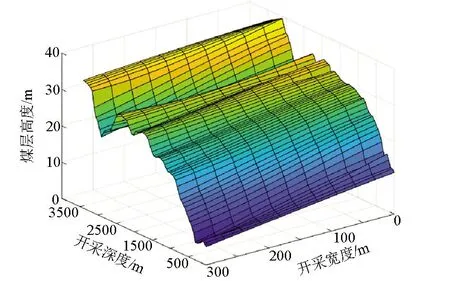
图6 单层DEM模型Fig.6 Single layer DEM model

4.2 基于Three.js的三维模型建立

Three.js 是一种基于javascript编写的第三方WEBGL库[18]。由于其速度快、易用性强、易于交互等特点，近年来被广泛应用于三维建模可视化领域。本文运用Three.js平台实现浏览器端三维模型建立，并实现人机交互操作。

人机交互功能主要采用Three.js 中的THREE. OrbitControls控件实现，在这种实现模式下，用户可以通过鼠标对界面图形进行放大、缩小、旋转、平移等相关操作，从不同的角度观察工作面煤层分布情况。如图8所示，其中黄色为矸石，深色为煤层。

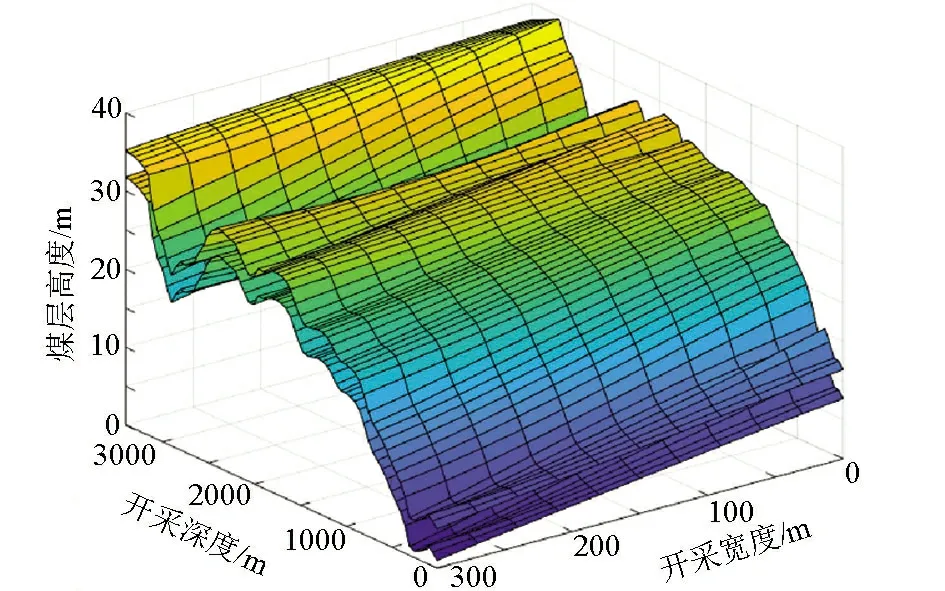
图7 多层DEM模型Fig.7 Multi-layer DEM model

图8 人机交互Fig.8 Human-computer interaction

5 结论

论文以神东集团大柳塔煤矿604工作面的实际数据，运用本文提出的UPSO-Kriging插值法对工作面分层结构的高程进行预测，进而基于规则网格法构建DEM数字高程模型，以Three.js为平台实现了浏览器端综采工作面三维可视化，并与传统的Kriging算法和PSO-Kriging算法进行对比，结果表明，利用UPSO-Kriging方法求得的空间插值数据更能反映实际的地质特性，能够比较准确地反映工作面地质结构。从实用意义上说,工作面煤层赋存状态三维可视化有着十分重要的意义，可以为煤炭企业的透明开采、智能开采、分质开采提供依据。