基于天气影响的风电功率分类预测模型研究

黄 健，季克勤，陈梓翰，郑 庆

(国网浙江电力有限公司 金华供电公司，浙江 金华 321000)

在当前高风电渗透率电网大背景下，精确的风电功率预测结果有助于改善电网内“源网荷”间的互动效率，对未来电网的建设发展以及提高电网内综合能源利用率具有重要意义[1]。

现有风电功率预测技术分为物理预测法、统计预测法、学习预测法以及组合预测法等。物理预测法通过采集风电场所在位置的物理信息和气象数据，建立风电转换模型进行预测，因无需历史运行数据常被用于新建风电场的功率预测。例如文献[2]在新建风电场内建立了计及风电场局地效应与风电机组尾流影响的风电功率物理预测模型。统计预测法通过大量历史风电功率数据在得出风电场运行规律的基础上，建立风电功率预测模型。例如文献[3]基于大量数据的统计分析研究，建立了基于自回归滑动平均模型风电功率预测系统；文献[4]利用风电场历史运行数据，建立了基于马尔科夫链的风电功率预测模型。学习预测法是基于人工智能技术兴起的一种预测技术，通过准确地刻画风速等数据与风电功率间的非线性关系得到最终的预测结果。例如文献[5]，采用深度学习算法深入挖掘了风电场历史运行数据间的非线性关系，建立了基于深度学习算法的风电功率预测模型。组合预测法则是利用以上不同算法的优势建立起的一种风电功率组合预测模型。例如文献[6-7]，通过将不同单一预测法进行优化组合，使预测模型能够发挥不同预测方法在预测过程中的优势，从而提高风电功率预测精度。

风电场输出功率受风电场所在位置的气候环境特征影响较大。不同的气候环境特征，对风电场的出力情况具有不同程度的影响。传统风电功率预测模型在进行风电功率预测时，并未考虑气候环境的变化过程对风电场出力的影响，预测精度仍存在提升空间。基于此，本文建立了一种基于天气影响的风电功率分类预测模型。根据各层高风速与风电场输出功率间的相关性检验结果以及风电场输出功率理论表达式确定了预测模型输入量，并由风电功率和各影响因素序列的自相关检验结果确定了影响风电场输出功率的时间尺度，以上2点为预测模型输入数据内容的确定提供了理论依据。确定预测模型输入数据内容后，在分类预测建模时，为简化天气过程聚类时的计算、实现分类结果的可视化，采用了深度学习自编码技术对输入数据进行降维处理，并利用改进的K-means聚类法进行了天气过程的聚类划分，根据聚类结果利用广义回归神经网络(Generalized Regression Neural Network，GRNN)算法对风电场输出功率进行分类预测。最后通过实际算例验证了本文方法能够获得更加有效的风电功率预测结果。

1 风电功率影响因素分析

1.1 风机运行机理分析

分析风电机组的运行机理，有助于更好地挖掘影响风电场输出功率的各类影响因素。风能是由大气环境中的空气流动所产生的，风力发电则是利用风电机组的叶片对流动的风能进行捕捉，进而实现能量的转化，生产出日常生产生活所需的电能[8]。实际运行过程中，某一时刻的风能通常满足式(1)所示函数表达形式。

E=0.5ρAv3

(1)

式中，E为对应时刻的风能；ρ为空气密度；A为风机叶片的捕捉面积；v为风速。

根据贝兹理论[9]的研究可知，在式(1)所示的风能条件下，风机能够获得式(2)所示的最大输出功率。

Pmax=0.296ρAv3

(2)

将式(1)和式(2)相结合，可以求得式(3)所示的风机极限转化效率Cp。

(3)

以上均为理想条件下的风电机组电能生产过程，实际中受设备状态等多重因素的影响，风机转化效率必然小于0.593。为将理论模型与实际过程相结合，提出了式(4)所示的风机实际输出功率函数表达式。

P=0.5CpρAv3

(4)

从以上风机的运行机理的分析过程中可以看出，风电场的输出功率会受到风电机组的运行效率、风速、风向、空气密度以及风机设备型号等多重因素的影响。

同时，空气密度以及风电机组的运行效率等因素还会受到气压、相对湿度以及环境温度等多重因素的影响，风电机组的各个影响因素间仍会存在有一定内部关联关系。所以，在进行风电功率预测时，可以选取风电场所在位置的风速、风向、温度、气压、相对湿度天气预报数据，作为预测模型的输入数据。

受场站内设备型号的影响，不同层高的风速与风电场输出功率间存在一定的差异性，风速的选取过程中按照式(5)计算风电场内各层高风速与风电场输出功率的皮尔逊相关系数进行选取，风向可以选取与风速相同层高的数据。

(5)

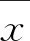
场站内各层高风速与风电场输出功率的皮尔逊相关系数计算结果见表1。

根据表1，最终选取70 m层高风速作为最终的风速研究对象。将对应的70 m层高风向数据作为风向研究对象，同时为避免风向数据过0时的跃变对模型预测精度的影响，将风向数据转化为了连续变化的正余弦值。除以上两参量的选取外，由于其余各参量与风电场输出功率间的相关系数较低，且这些参量的选取是通过风机运行机理的分析过程所确定的所以不在进行相关系数的计算。

表1 风速与风电场输出功率皮尔逊相关系数计算结果

1.2 风电功率主要影响因素作用的时间尺度分析

无论是风力发电系统还是天气的变化过程，两种均具有一定的惯性特征，也即当前的状态量会受前一时刻甚至一定时段内的状态量变化影响较大。基于以上原因，在进行风电功率预测时不能仅进行影响因素的选取，还需要分析各影响因素对风电场输出功率作用的时间尺度。在进行时间尺度的选取时，本文首先利用式(6)所示的函数表达式计算延迟步长条件下的自相关系数。

(6)

根据式(6)，计算得到图1所示的各影响因素及风电功率序列的自相关系数计算结果。

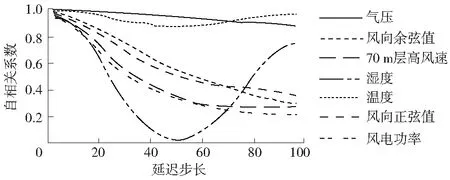
图1 自相关系数检验结果

此次样本集中数据的采样间隔为每15 min/次，1 d中对各影响因素的采样量为96次。根据样本数据的采样特征绘制了图1所示的延迟步长在0～96内各影响因素以及风电功率序列的自相关检验结果，以此得到1 d内各影响因素内部所具有的关联特征。从图1的变化过程可以看出，温度和气压的自相关检验结果始终在大于0.9的高度自相关条件下，原因在于这2个参量受季节变化的影响较大，在1 d内差异性较小，可以忽略这2个因素对风电功率时间尺度的影响；湿度的自相关检验结果在1 d内呈先下降后上升的变化趋势，由此可知湿度的变化特征在1 d内具有一定的规律性；除以上影响因素，其余的70 m层高风速、风向正余弦值以及风电功率序列的自相关检验结果则呈现出迅速下降的变化趋势。

为了提高风电功率预测模型的预测精度，简化预测模型建模时输入数据的复杂性，本文以自相关系数0.8作为截断选取了待预测点前16个观测点的数据(4 h内的数据)作为输入数据进行风电功率的预测。

2 风电功率主要影响因素作用过程划分

2.1 数据构建方式

根据上文风电功率主要影响因素以及时间尺度的选取结果，将风电功率预测过程所需的数据集进行整合得到式(7)所示第i个时间点所对应的风电功率预测模型输入数据内容。

(7)

式中，Ti-15、Hi-15、Pi-15分别为时间点i之前4 h处的温度、湿度、气压数据，三者均为一个点数据；V、usin、ucos分别为时间点i之前4 h内的风速、风向正余弦值，三者均为集合数据。

根据式(7)可以看出，对应于时间点i处的风电预测模型输入数据集为一个1×51维的数据结构形式。

2.2 聚类划分过程

2.2.1 自编码网络技术

根据数据构建方式的介绍，为了找到一个天气过程对风电场输出功率的影响，构建了一个1×51维的样本数据。高维样本数据既不能在便于观察分析的可视化二维空间能进行展示，也会因过高的样本维度增加建模过程的计算量，进而影响到分析过程和预测模型的准确性。为了排除以上问题对预测过程的影响，本文采用自编码技术对所构建的样本数据进行了降维处理。

自编码网络技术(AutoEncoder，AE)通过输入等于输出的方式构建了一种典型的无监督神经网络算法模型[10]。自编码网络的结构如图2所示。

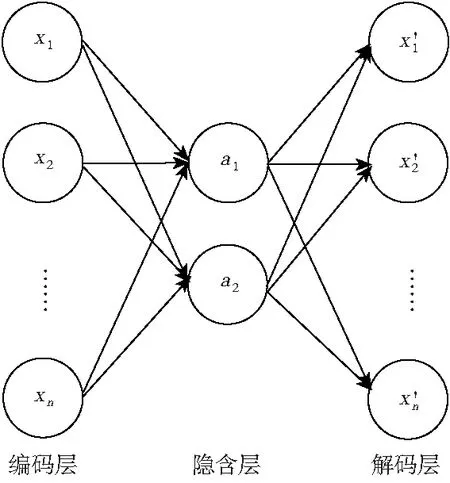
图2 自编码网络结构

假设输入数据为x，输出数据为x′，x、x′∈Rn×1，n为输入输出数据的维数，自编码网络的编码过程可以表示为式(8)所示的函数表达形式。

y=f(x)=s(ωx+b)

(8)

式中，s(·)为激活函数，为进一步简化计算过程，选取具有一定稀疏能力的ReLU函数；ω和b为自编码网络中隐含层的权值和阈值，其结构与输入数据相同；y为隐含层输出，y∈Rr×1。

输入数据在经过编码计算后，还需要经过自编码网络的解码计算，其函数计算过程如式(9)所示。

x′=g(y)=s(ω′x+b′)

(9)

式中，ω′∈Rn×r；b′∈Rr×1；r为隐含层节点数。

经过以上计算过程得到，自编码网络的网络参数调整过程同传统神经网络相似[11]。经过自编码网络的降维处理后，最终得到了图3所示的处理结果。

2.2.2 改进K-means聚类算法

具有高维特征的天气变化过程在图3所示的二维平面内得到了展示。为了能够进一步提高风电功率预测模型的预测精度，本文在自编码网络降维处理的基础上，采用K-means聚类算法对不同的天气变化过程进行聚类划分。K-means算法的聚类过程如下：①在图3所示的样本数据中选定K个样本点作为样本数据的初始聚类中心；②计算所有样本点到①中所选定的初始聚类中心的距离，并将样本点划分到与其最近的初始样本点所属的类别中；③根据②中进行的聚类结果，重新计算每一类样本的质心选出新的样本聚类中心；④重新计算所有样本同新样本聚类中心的距离，并重新计算新聚类中心与原始聚类中心之间的距离，如果两者距离小于一定的阈值则认为达到了预期聚类效果，终止聚类过程，否则重复进行②—④步，直到满足最终的阈值设置结果。

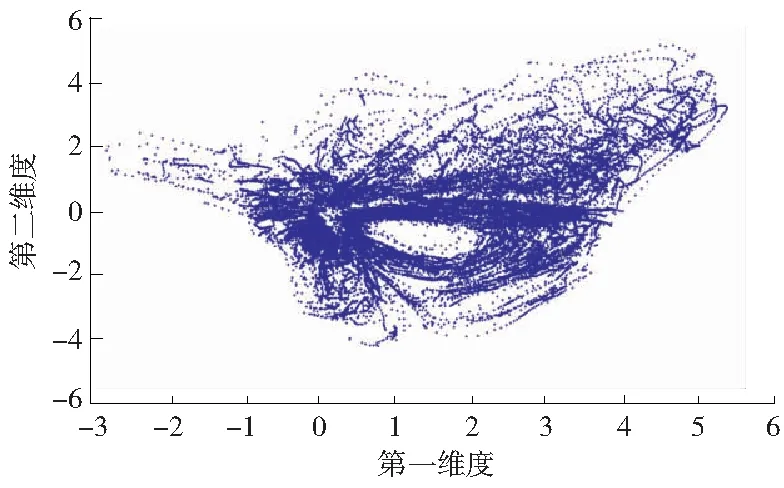
图3 自编码网络降维处理样本

在K-means聚类过程中，选取了式(10)所示的2个样本在二维空间中的欧氏距离作为样本点间距离的计算依据。

(10)

式中，x1和y1分别为样本1在第一维度和第二维度的值；x2和y2分别为样本2在第一维度和第二维度的值；d为最终计算得到的2个样本间的欧氏距离。样本质心的计算为此类样本中所有样本点各个维度数值的平均值。

由于K-means聚类算法在进行聚类时K值为随机设置的，不同的K值设置结果会对聚类结果产生很大的影响[12]。为了能够得到最佳的聚类结果本文将不同K值设置条件下，聚类结果的类内平均距离与类间平均距离的比值作为最终的评价指标对比了不同K值设置结果的聚类效果。类内平均距离代表聚类后同一类样本的聚集程度，类间平均距离代表聚类后不同类样本间的离散程度，两者的比值越小则证明获得了更好的聚类效果。不同K值设置条件下聚类效果评价指标的变化情况如图4所示。

从图4的评价指标变化过程可以看出，当设置聚类数为8时能够得到最佳的聚类效果。根据以上结果，最终得到图5所示的样本聚类结果，每一类样本的质心用三角形进行了标注。

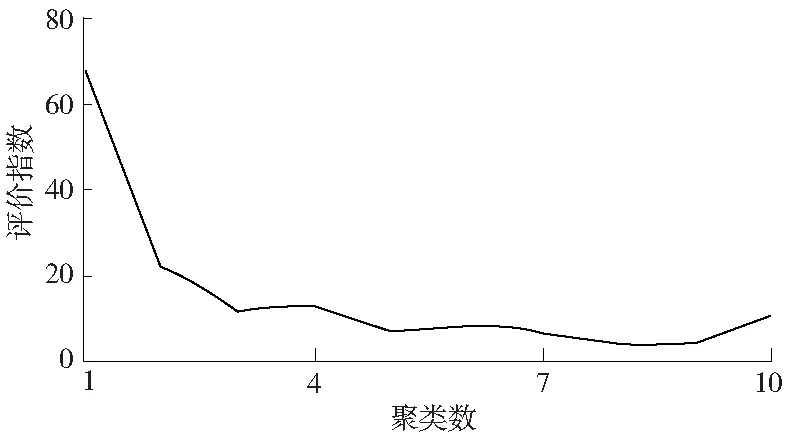
图4 聚类效果评价指标

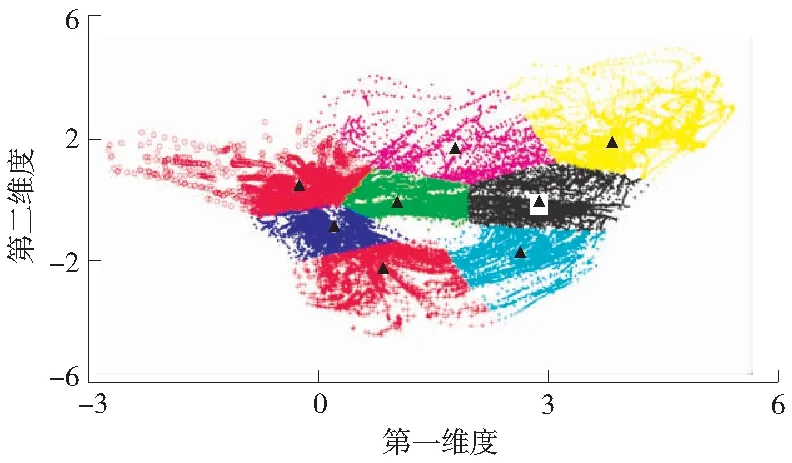
图5 聚类结果

3 风电功率预测模型

3.1 GRNN网络

GRNN网络是基于非线性回归分析理论所形成的一种径向基神经网络，具有很强的非线性映射能力和稳定的柔性容错网络结构[13]。GRNN网络包含有4层网络结构，分别是输入层、模式层、求和层以及输出层[14]。

(1)输入层。输入层节点数与待学习样本中输入数据的维数相同，输入层神经元间无连接结构，直接将输入数据以线性传递的方式传递至下一层网络中[15]。

(2)模式层。模式层的网络节点数等于学习样本数，模式层的网络节点对应于不同的样本数据[16]，模式层的网络传递函数如式(11)所示。

(11)

其中，i=1，2，…，N。

(3)求和层。在求和层中对所有模式层中的神经元进行算术求和以及加权求和[17]，2种求和模式的函数表达形式如式(12)和式(13)所示。

(12)

(13)

式中，k为输出向量维数；Yi为求和层节点i的权值矩阵；yij为求和层节点i在j维的权值。

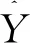
(14)

根据式(14)可知，GRNN网络的输出为式(15)所示。

(15)

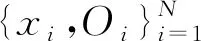
(16)

式中，xi和Oi为随机变量的输入和输出；p为输入量的维数。

4 算例分析

4.1 预测流程

根据以上GRNN网络的介绍，按以下步骤进行风电功率预测。

(1)将降维处理后在图5中展示的每一类天气过程样本数据作为输入数据，对应的风电功率值作为输出数据，进行不同天气类型条件下GRNN网络模型的训练。

(2)聚类划分处理后，每一类样本数据的数据量相比于未分类时总的样本数据量均减少了很多。为使预测模型得到更好的训练效果，并获得适用于每类样本数据的平滑因子，采用交叉验证的方式训练适用于每一类样本数据的GRNN模型。

(3)按照式(7)所示的方式对待预测日的样本数据进行重构，并将重构后的数据采用自编码网络技术进行降维处理。

(4)计算降维处理后的待预测日数据与每一类样本数据间的欧氏距离，将待预测日样本数据划入与其距离最近的一类中，最后采用对应类别内训练好的GRNN模型进行风电功率预测。

4.2 预测结果

根据以上预测流程，最终得到图6所示的GRNN风电功率预测结果。

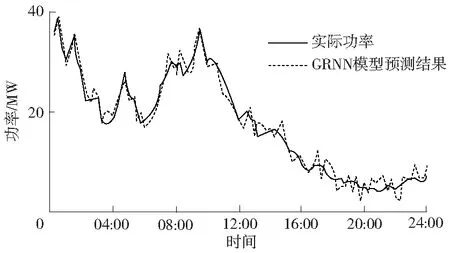
图6 GRNN模型风电功率预测结果

为进一步验证本文模型预测结果的有效性，选取相同的输入输出数据建立了BP神经网络风电功率预测模型，预测结果如图7所示。

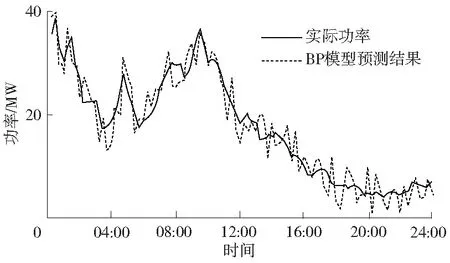
图7 BP神经网络风电功率预测结果

4.3 评价指标

本文采用均方根误差、合格率以及累计电量损失作为预测结果的评价指标，通过以上指标的对比计算，进一步证明了本文模型预测结果的有效性。

(1)均方根误差。均方根误差反映的是预测结果总体偏离真实值的程度[19]，其对应的计算方法如式(17)所示。

(17)

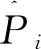
(2)合格率。合格率反映的是预测结果能够应用于电网调度运行的数量[20]，其对应的计算方法如式(18)所示。

(18)

其中，Bi为1时表示该点的预测结果合格，反之取0；T为合格阈值，一般取0.2。

(3)累计电量损失。电量损失是风电场实际运行过程中的一个重要考核指标。为衡量不同模型预测结果的有效性本文引入了累计电量损失这一评价指标，累计电量损失是整体预测结果偏离真实值的累计，通过计算该值得到不同预测模型最终的损失电量，其对应的计算方法如式(19)所示。

(19)

综上所述，最终得到评价指标见表2。

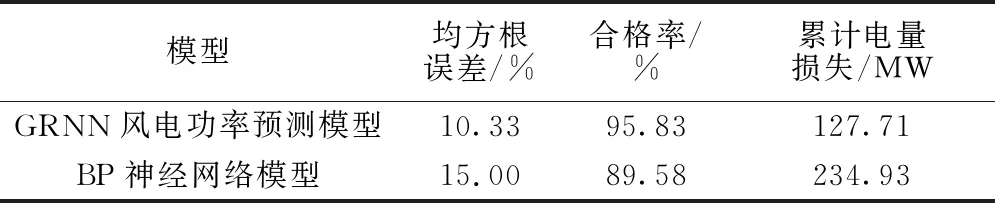
表2 评价指标

5 结论

根据以上风电功率预测模型的预测结果可以看出，本文采用GRNN网络所建立的基于天气过程影响的风电功率预测模型在均方根误差上相比于传统BP神经网络所创建的风电功率预测模型降低了4.67%，预测结果的合格率方面提高了6.25%，共计减少了107.22 MW累计电量损失。由此可见，本文模型在进行风电功率预测时具有一定的有效性。