基于PSO-ELM模型的冻融期土壤蒸发预报
2021-08-04陈军锋郑秀清崔莉红杨小凤
刘 磊,陈军锋,薛 静,郑秀清,杜 琦,崔莉红,杨小凤
(1.太原理工大学水利科学与工程学院,太原030024;2.山西省水文水资源勘测局太谷均衡实验站,山西太谷030800)
0 引 言
冻融期气候条件恶劣,给土壤蒸发量的实测带来了较大困难[1]。由于土壤水分相变导致冻融土壤蒸发机理复杂[2],传统经验公式难以计算冻融期土壤蒸发量。因此,部分学者开始在土壤水热耦合模型的基础上计算冻融期土壤蒸发量[3,4],但这些模型通常要求输入大量地面观测资料、计算过程复杂且参数率定困难,较难应用于实测资料匮乏地区的冻融期土壤蒸发量预测。冻融期土壤蒸发量与外界气象条件具有很强的非线性关系。人工智能算法具有极强的学习能力,通过非线性拟合的方式解决实际问题且预测精度较高[5],可较好地用于冻融期土壤蒸发的预测[6-8]。学习速度快、泛化性能好的极限学习机在非线性函数拟合、回归中具有较为明显的优势。但是,由于该算法的输入权值及阈值随机给定,不能直接找到最优的参数,影响模型的泛化性能及稳定性,导致预测精度不高。因此,众多学者通过各种优化算法对极限学习机回归预测过程中存在的问题进行了优化[9,10]。本文将冻融期土壤蒸发实测数据以及气象站资料通过随机函数处理作为输入样本,提出了基于PSO-ELM 模型的冻融期土壤蒸发预测方法,并与ELM 模型及GA-ELM 模型的预测精度进行对比,为冻融期土壤蒸发的预测提供了新的思路和方法。
1 材料与方法
1.1 试验区概况
试验区位于山西省太原盆地东部,山西省水文水资源勘测局太谷均衡实验站,地理位置37°26'N、112°30'E,海拔高度777 m,属大陆性干旱半干旱季风气候,多年平均(1954-2008年)气温9.9 ℃,多年平均降水量415.2 mm,多年平均水面蒸发量1 642.4 mm,多年平均风速0.9 m/s,多年平均相对湿度74%。
1.2 试验数据来源及处理
田间试验于2016年11月22日至2017年3月15日进行,气温、气压、风速、相对湿度、降水量、水面蒸发量、太阳辐射均通过气象站自动监测,气温、气压、风速、相对湿度、以每天8∶00、14∶00、20∶00 这3 个时刻的平均值作为该日数据,太阳辐射采用基于日照时数的Ångström-Prescott 模型计算。
表层土壤含水率采用烘干法监测,地表土壤温度采用埋置的热敏电阻测定,土壤蒸发量通过PVC 微型蒸发器采用称重法监测,监测时间均为8∶00-9∶00,监测周期5~7 d,整个试验期共监测17 次。将表层土壤含水率、地表土壤温度以及土壤蒸发量17 组数据通过线型内插得到114 组日数据,与对应的气象日数据组成114组样本数据。
1.3 模型建立
1.3.1 极限学习机
极限学习机(Extreme Learning Machine,ELM)克服了传统神经网络训练速率慢、容易陷入局部最优及对学习率敏感等缺点[11],是一种由输入层、隐含层以及输出层3 层组成的单隐含层无反向传播算法的前馈型神经网络,输入层、隐含层与输出层间由神经元相互连接,结构示意图见图1。极限学习机模型主要步骤为:①对114组样本数据进行归一化处理;②将冻融期土壤蒸发的9个影响因素作为输入层的输入变量,土壤蒸发量作为输出层的输出变量,经过多次验证后隐含层神经元的个数设置为14;③初始化输入层与隐含层间的连接权值ω和隐含层神经元偏置b;④选择隐含层的激活函数为“sigmoidal”函数,通过广义逆矩阵理论计算隐含层的输出矩阵H;⑤计算隐含层与输出层之间的连接权值β:
式中:H+为H的Moore-Penrose广义逆;T为期望输出矩阵。
1.3.2 PSO-ELM 模型的构建
粒子群算法(Particle Swarm Optimizatian,PSO) 是由Eberhart 和Kennedy 通过对鸟群捕食行为研究提出的一种全局优化算法[12,13],采用位置、速度以及适应度值3 个指标来描述粒子的特征,通过比较粒子的适应度值确定个体极值、群体极值。根据公式(2)、(3)更新粒子的位置与速度,粒子每次更新都要重新计算适应度值、确定个体极值和群体极值,一直反复迭代,从而实现在解空间中的寻优。
式中:Vkd(t+ 1)为粒子k在第t+1 次迭代中第d维的速度;w为惯性权重,一般取0.9;c1,c2为学习因子;r1,r2为[0,1]范围内的随机数;Pbestkd(t)、Gbestkd(t)表示粒子k在个体及群体中的极值位置。
本文采用粒子群优化算法对ELM 模型的输入权值和阈值进行优化,每一个粒子都可以看作一个预测土壤蒸发的ELM模型,采用粒子的位置信息表示ELM 模型的输入权值和阈值,粒子维数D及粒子群中第k个粒子θk表示为:
式中:t、n分别为输入层和隐含层神经元个数;分别为输入权值和隐含层阈值,均为[-1,1]内的随机数,1<i<n,1<j<t。
以均方误差(MSE)作为粒子的适应度函数,寻找所有粒子中的最优值,建立PSO-ELM 模型,具体流程见图2。粒子群算法参数设置为:粒子群规模为30,最大迭代次数为200,学习因子c1=c2=2,惯性权重wmax=0.9,wmin=0.1,粒子维数为140。
1.3.3 GA-ELM 模型的构建
遗传算法(Genetic Algorithms,GA)是由美国Holland 教授于1962年提出的,是一种模拟生物遗传进化建立的并行随机搜索最优化方法[14]。遗传算法将需要优化的ELM 模型的输入权值及阈值进行编码,然后根据所选的适应度函数,通过遗传过程中的选择、交叉和变异在群体中进行筛选,得到适应度最优的个体,建立GA-ELM 模型,具体流程见图3。遗传算法参数设置为:初始种群数量为20 个,个体编码方式为二进制,交叉概率为0.7,变异概率为0.01,最大遗传代数为100。
2 结果与分析
2.1 评价指标
为了评价冻融期土壤蒸发预测精度,本文以均方根误差(RMSE)、平均相对误差(MRE)、平均绝对误差(MAE)以及决定系数R2作为预测结果的评价指标。评价公式如下:
式中:yi、分别为土壤蒸发量实测值和预测值。
2.2 随机函数对于预测结果的影响分析
2016-2017年冻融期可分为不稳定冻结期(2016年11月7日至12月26日)、稳定冻结期(2016年11月27日至2017年2月2日)及消融解冻期(2017年2月3日至3月15日)[16]。不稳定冻结期气温在0 ℃上下波动,土壤表层出现“昼融夜冻”的现象,土壤蒸发较为强烈;稳定冻结期冻层深度持续增加,稳定密实的冻土层令表层和下层土壤水的联系切断,土壤蒸发量较少;消融解冻期气温回升,土壤冻层呈现自表层向下及下层向上的“双向融化”的现象,融化后的水分补充土壤表层导致土壤蒸发强烈。3个阶段由于土壤物理性质不同,即使在相同外界气象条件下土壤蒸发量也会存在较大差异。前人对冻融期土壤蒸发的模拟均是以不稳定冻结期、稳定冻结期的实测土壤蒸发量及其9个影响因素作为训练样本,来预测消融解冻期的土壤蒸发量[9-11],预测结果代表性较差。本文在前人研究基础上,对未随机排列的数据和随机排列后的数据分别通过PSO-ELM 模型进行预测,预测精度结果变化见表1。样本数据随机排列后的预测精度相较于未随机排列有了较大提升,减少了特定冻融阶段的土壤蒸发量作为训练样本或预测样本对预测结果的影响。

表1 随机函数处理前后评价预测精度变化Tab.1 Change of prediction accuracy before and after random function processing
2.3 预测结果分析
为了说明PSO-ELM 模型的优势所在,在生成的114 组样本数据中,通过随机函数处理将数据打乱,随机选取其中90组作为训练样本数据,剩余24 组作为测试样本数据。分别使用ELM 模型、GA-ELM 模型和PSO-ELM 模型对冻融期土壤蒸发量进行预测,对比3 种预测结果来说明PSO-ELM 模型的优势。预测结果见图4,评价指标计算结果见表2。
由图4 及表2 可见,3 种模型预测值均分布在实测值上下两侧,其中PSO-ELM 模型拟合效果最好,GA-ELM 模型次之,ELM 模型最差,PSO-ELM 模型决定系数R2为0.993 6,均方根误差为0.010 9 mm/d,平均相对误差为4.91%,平均绝对误差为0.007 9 mm/d。
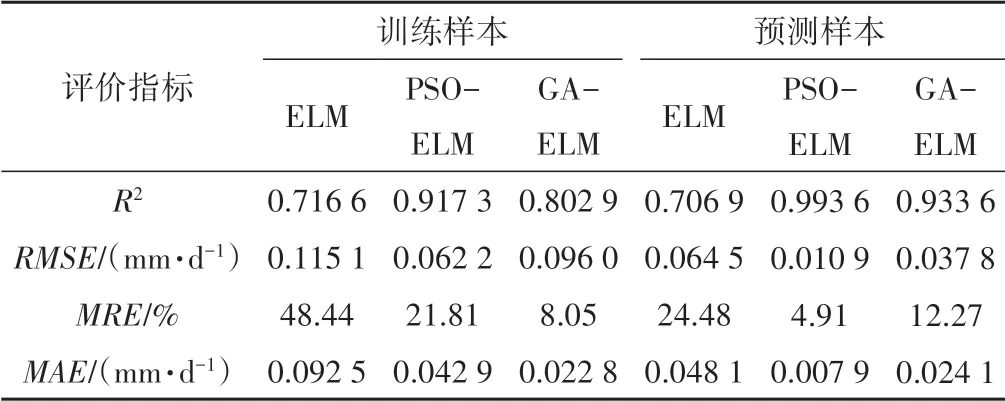
表2 3种不同模型评价指标计算结果Tab.2 Calculation results of evaluation indexes of three different models
3种模型土壤蒸发训练样本和实测样本的实测值及预测值的绝对误差和相对误差结果分析见图5。单一ELM 模型训练及预测误差均大于允许误差(20%),说明在冻融期土壤蒸发资料匮乏情况下单一ELM 模型由于输入权值和阈值随机给定导致难以寻找到最优参数,容易出现欠拟合现象,降低预测精度;GA-ELM 模型与PSO-ELM 模型相比训练误差相差不大,但预测误差却远大于PSO-ELM 模型,说明当训练样本数量较少时GA-ELM 模型在训练过程中容易出现过拟合现象,降低了冻融期土壤蒸发预测的精度;PSO-ELM 模型绝对误差上限、相对误差上限、绝对误差上四分位数、相对误差上四分位数、绝对误差中位数、相对误差中位数等各项指标均小于其他2个模型并且处于允许误差范围内,表明PSO-ELM 模型更适合用来预测冻融期土壤蒸发。
综上可知,3 种模型中PSO-ELM 模型预测精度最高、预测效果最好,GA-ELM 模型次之,单一ELM 模型精度最低,说明PSO-ELM模型更适用于冻融期土壤蒸发的预测。
3 结 论
(1) 通过与单一ELM 模型及GA-ELM 模型对比发现,PSO-ELM 模型的预测样本预测值与实测值拟合程度最高,预测效果最好,PSO-ELM 模型的决定系数为0.993 6,均方根误差为0.010 9 mm/d,平均相对误差为4.91%,平均绝对误差为0.007 9 mm/d,模型决定系数大于0.9,平均相对误差小于10%,说明所建立的PSO-ELM 模型可较好用于冻融期土壤蒸发预测。
(2)通过随机函数对样本数据进行处理减少了特定冻融阶段的土壤蒸发量作为训练样本或预测样本对预测结果的影响,提高了模型的预测精度,为干旱、半干旱地区冻融期土壤蒸发预测提供了一种新的思路。
