基于修正SSTk-ω湍流模型的建筑群风环境数值分析

汪 阔,沈 炼,韩 艳,胡 朋,杨 瑛

(1.长沙理工大学 土木工程学院，湖南 长沙 410076；2.湖南大学 土木工程学院，湖南 长沙 410082；3.长沙学院 土木工程学院，湖南 长沙 410022；4.湖南省建筑设计院有限公司，湖南 长沙 410012)

良好的室外风环境是城市居民正常生活生产的前提保障.目前主要研究手段有现场实测，风洞实验和数值模拟，数值模拟由于具有经济、可获取流场的详细分布等优点，近年来得到了广泛应用.如Du等[1]利用RANS方法对香港理工大学风环境进行了分析；Blocken等[2]利用RNGk-ε方法对埃因霍温理工大学的校园行人舒适风环境进行了分析，为城市行人风舒适性评估提出了大量建议；Ricci等[3]对意大利的一老街区进行了分析，得到了不同入口来流对城市冠层流场的影响，取得了较好的研究结论.但不足的是实际小区建筑形态复杂多样，很难获取小区内部风环境分布的普适性规律.也有许多学者采用标准模型对建筑风环境进行研究，以获取冠层内风环境分布的一般规律.如Coceal等[4-5]以4个均匀交错的建筑立方体为计算模型，得到了建筑物周边平均速度、剪切力和湍动能的详细分布；胡一东等[6]使用标准k-ε模型对9种典型建筑小区进行了分析，得到了平均风速与阻塞率的相对关系；Kono等[7]利用大涡模拟对6种不同密度建筑模型进行了分析；马建等[8]采用RNGk-ε湍流模型分别对单幢方形截面建筑和多幢矩形截面建筑组成的建筑群周围的风速进行了数值模拟和风洞试验，并对数值模拟提出了合理建议；于丽波等[9]利用了四种不同的湍流模型对某超高层三塔连体建筑进行了数值模拟，发现RNGk-ε与SSTk-ω湍流模型模拟结果与风洞试验吻合最好；Azli等[10]通过大涡模拟对五种均匀交错块阵列和一种非均匀交错块阵列建筑群进行了数值模拟，得到阵列模型平均风的空间特征；Zhang等[11]采用RNGk-ε湍流模型研究了三种不同建筑布局对垂直风速影响，发现45°风攻角对结构周围的风场有显著影响；Kubota等[12]则对不同建筑密度下行人高度风环境进行了风洞试验研究，指出了建筑覆盖率与平均风速之间存在较强的相关性，为住宅区的风环境评估提供了相关准则.

上述研究对建筑物的布局与形态进行了广泛分析，得出了大量有用结论，但不足的是研究对象相对单一，没有考虑不同形态下建筑冠层的风场分布，且当前数值研究对湍流的考虑相对缺乏，已有考虑湍流效应的研究由于没有考虑数值流场中的湍流耗散问题，使得模拟精度相对较低.因此，本文基于上述研究的不足，采用SSTk-ω自平衡湍流模型，对建筑密度、不同高度和错落度3种建筑形态下的城市冠层流场进行了深入分析[13-14]，获取了不同建筑形态下平均风速与湍动能的详细分布，揭示了不同建筑形态下流场的分布规律，相关研究可供绿色城市建设与规划参考.

1 数值理论

1.1 控制方程

SSTk-ω湍流模型比k-ε湍流模型更适用于具有逆压梯度流动或分离流动的计算，因而前者更广泛地应用于大气边界层钝体绕流的计算中，基于该模型下的湍流控制方程为

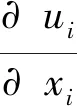
(1)

(2)

(3)

(4)

(5)

1.2 自保持SSTk-ω修正模型

采用SSTk-ω模型时，需要满足：(1)压强为常数；(2)剪切应力为常数；(3)湍动能与比耗散率满足各自的输送方程[15].

湍动能k与比耗散率ω表达式为

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

其中：α∞、β*及βi为湍流模型中的系数，F1为混合函数，σω,2为湍流模型常数，Cu1、Cu2为湍流边界条件参数，可由试验数据拟合得到，C1k、C2k、C1ω、C2ω、C3ω及C4ω是考虑相关系数引入参数，采用上述理论对源项进行添加，从而实现模拟过程中k、ω的自保持.

本文采用对数律的风剖面表达式为

(14)

2 数值模拟验证

2.1 模型介绍与网格划分

为了验证自保持修正模型的准确性，利用Fluent对二维流场进行数值模拟，其中入口边界条件由风洞试验数据拟合而成[16-17]，计算域尺寸设定为9 m×3 m，区域没有放置任何物体，计算域划分设置如图1所示，采用结构化网格进行网格划分，并对底部网格进行加密，网格尺寸延伸率为1.15，最小网格尺寸为0.001 m.

图1 计算域示意图Fig.1 Computational domain

2.2 边界条件与计算方法

计算域入口采用速度入口，出口采用压力出口，上顶面采用自由滑移边界，下底面采用无滑移边界.计算过程中，设置不考虑源项和考虑源项两种情况，考虑源项时，各项参数设置见公式(15)～(17).压力与速度耦合采用SIMPLEC算法，动能方程、湍动能及比耗散率输送方程均采用二阶离散格式，残差收敛精度均设置为1×10-6，详细的入口计算参数为

(15)

(16)

(17)

2.3 模拟结果分析

对传统SSTk-ω和修正的SSTk-ω两种模型进行分析，无量纲高度采用1 m.如图2所示，由图2可知，其速度及比耗散率大体上能保持一致，但入口湍动能与其它位置的湍动能差异明显，说明不考虑源项时，该流场的k、ω未平衡.对于修正的SSTk-ω模型，从图3中可以发现各变量在不同位置均有较高程度的一致性，说明采用修正的方法能很好地实现大气边界层的平衡，本文将采用修正方法模拟所有工况.

图2 传统SSTk-ω模拟结果Fig.2 Simulation results by traditional SSTk-ω model

图3 修正SSTk-ω模拟结果Fig.3 Simulation results by modified SSTk-ω model

3 不同建筑形态下小区流场分析

3.1 模拟工况介绍

为研究不同建筑形态下的城市小区风环境，对不同建筑密度、平均高度和错落度三种形态作用下小区流场进行了详细分析，模拟工况如表1所示，数值模拟过程中，每种建筑形态均考虑建筑物与来流正交工况，不同建筑形态示意图如图4所示.

表1 模拟工况汇总Tab.1 Simulation cases

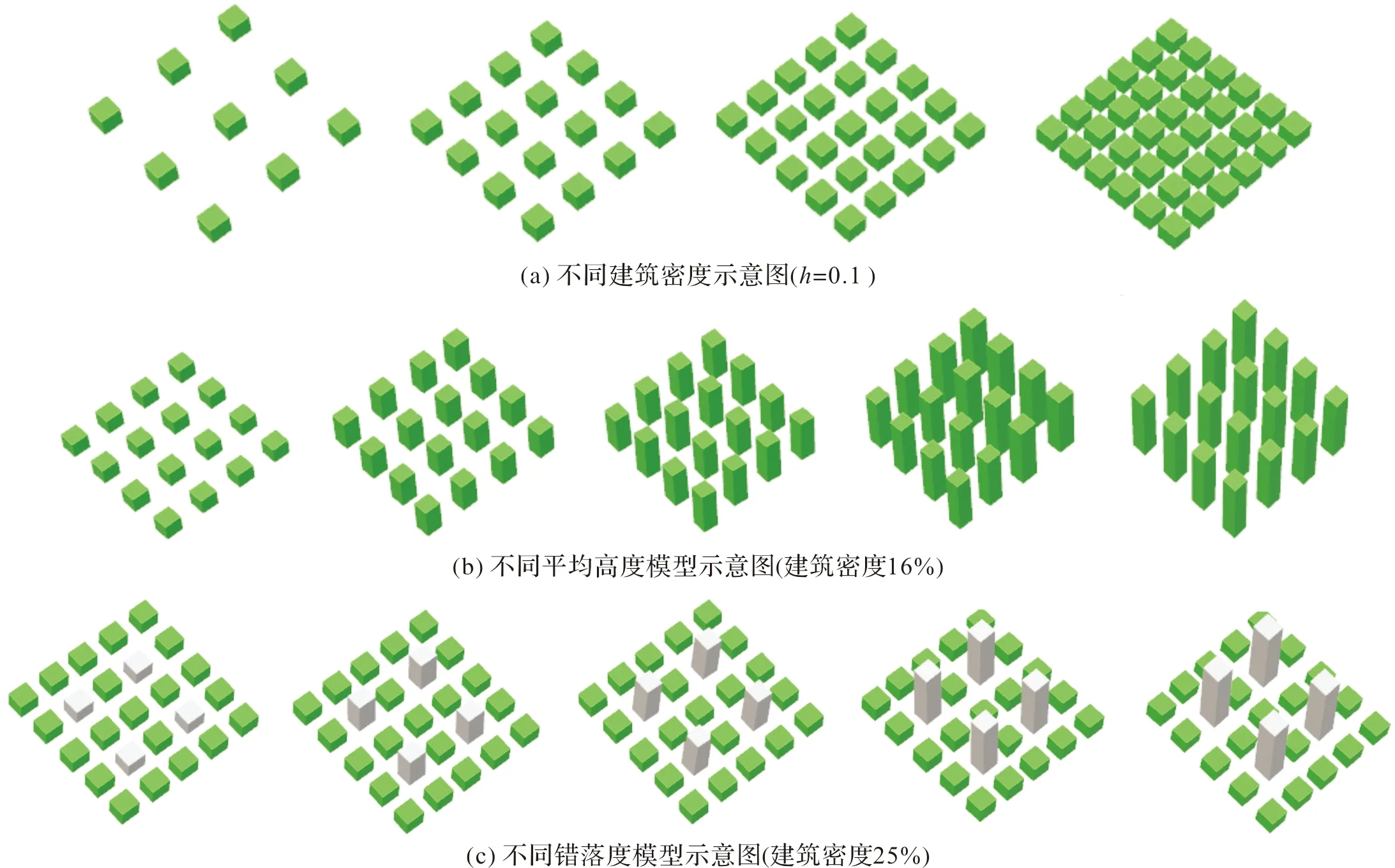
图4 不同建筑形态示意图Fig.4 Different building morphology

3.2 数值模拟参数设置

采用修正SSTk-ω自保持湍流模型，其计算方法和参数设置与2.2节一致，采用结构化网格，工况计算域如图5所示，网格划分过程中对建筑物附近以及尾流区域进行局部加密，模型表面网格尺寸最小0.001 m，网格尺寸延伸率为1.1，不同密度网格平面图如图6所示.

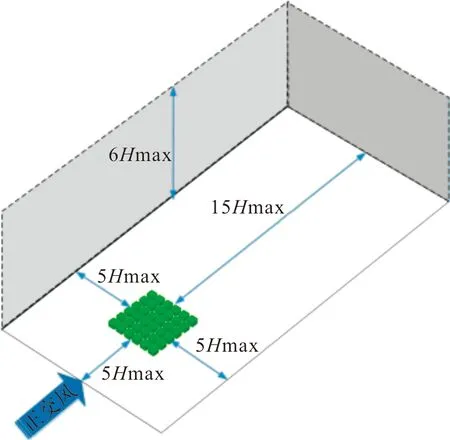
图5 计算域Fig.5 Computational domain

图6 小区模型局部网格Fig.6 Grid for different cases

模拟过程中，为保证计算精度，模拟前进行了网格无关性测试，建立了5万、44万和81万3种单体建筑网格，在建筑物周围区域，布置60个监测点监测其速度，将5万、44万和81万分别于风洞试验进行比较，最终选择44万网格模型的设置参数作为最终模型的网格划分依据参数.计算过程中，时间步采用0.001 s，所有计算均在处理器为Intelcore i9-7980 XE，12核24线程，内存32 G的工作站上展开.为验证数值模拟的正确性，对单体建筑模型进行的风洞试验，风洞试验在长沙理工大学风工程与风环境研究中心进行，试验过程中，对建筑物前后侧风剖面进行监测，与数值模拟结果对比如图7所示.从图中发现，模拟值与实测值吻合较好，因此验证了数值方法的正确性.

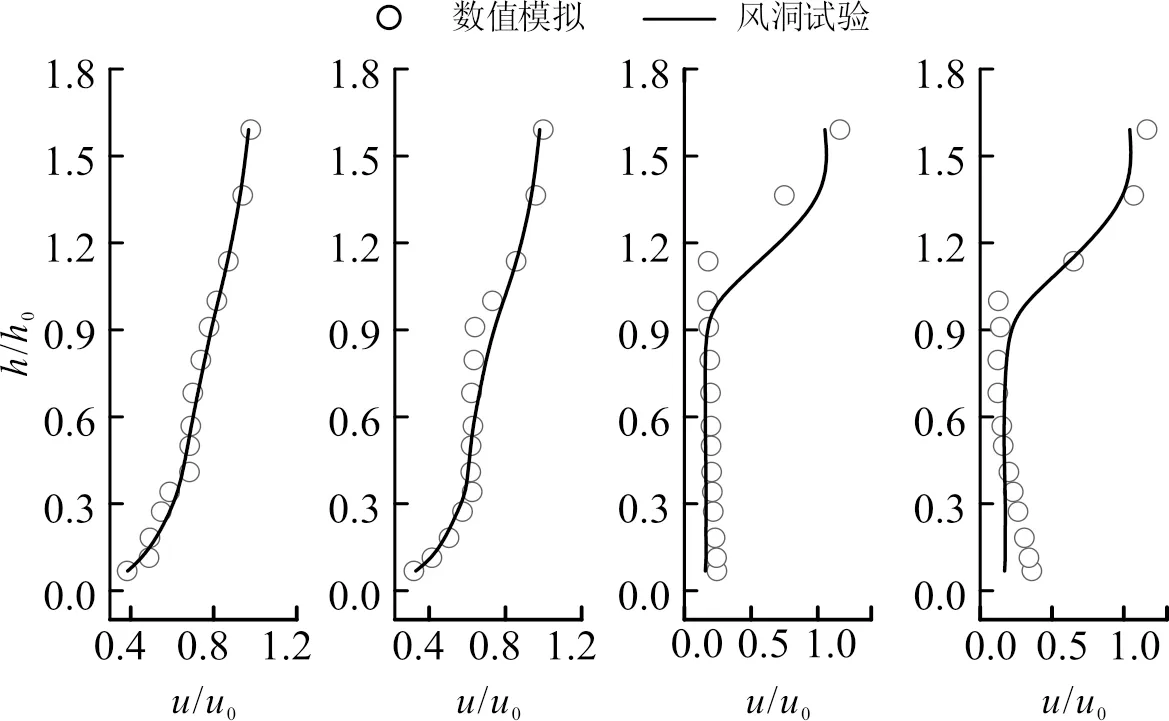
图7 风洞试验与数值模拟比较图Fig.7 Comparison of wind tunnel tests and numerical simulations

3.3 模拟结果与讨论

3.3.1 平均风速

对小区模型顺风向中心轴线进行速度监测，监测点布置如图8(a)所示，监测高度为两倍建筑高度，不同位置沿高度方向的速度分布如图8(b)所示.从图中可以发现风速在高于1.3倍建筑以后，其剖面与入口一致，但在1.3倍高度以下风速要明显低于入口来流，再次说明建筑物对风场产生了较大拖曳作用.

对图8(b)中6点(A1-A6)风速取平均，可得到该密度下的风剖面分布.同样，将9%，16%，25%和36%4种建筑密度工况进行汇总，得到的平均风剖面如图9(a)所示.对建筑高度为0.1 m，0.16 m，0.24 m，0.32 m和0.4 m 5种平均高度工况的平均风剖面进行汇总，其结果如图9(b)所示，5种错落度影响下的风剖面如图9(c)所示.从图9可以发现，根据无量纲风速大小可将风速依次划分为：紊乱区、增长区和稳定区.其中紊乱区风速杂乱无章，无明显规律，相对入口来流整体偏低，平均值为0.178uref，紊乱区影响高度与建筑物自身高度一致，对不同密度与高度而言，紊乱区的无量纲风速分布在0到0.2uref之间.对不同错落度而言，紊乱区无量纲风速落于0到0.44uref之间，说明错落度提升了紊乱区的风速上限值，增大了小区内风场的紊乱程度.

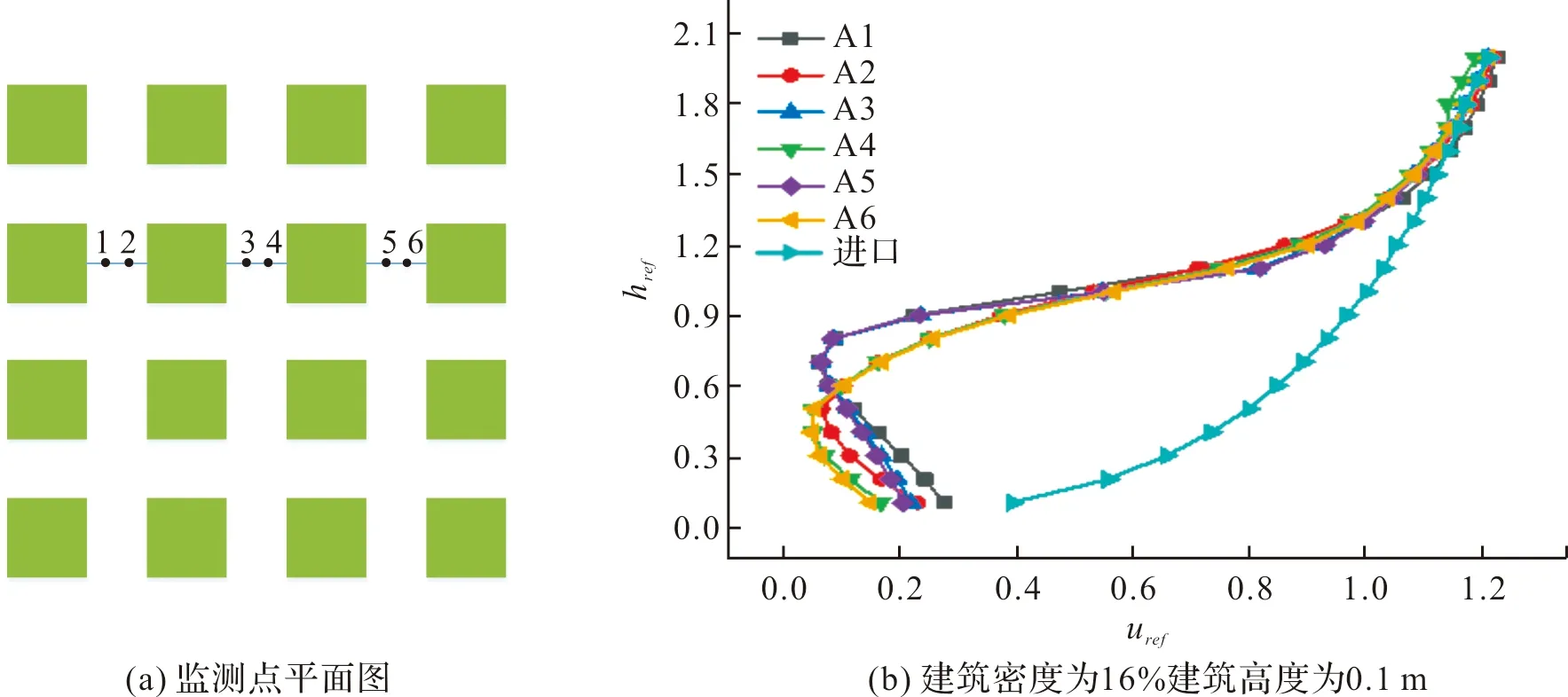
图8 不同风速监测点Fig.8 Wind velocity monitoring points

增长区指风场稳定增长区域，其所在高度一般为建筑平均高度的1～1.3倍区域，通过对比图9，增长区风速分布规律发现，增长区在高度方向占比较小，但速度具有急剧增加特征.从图9(b)中可以明显发现，五条曲线相互“平行”.对不同密度而言，无量纲风速增长区末端在0.9uref，而不同高度与错落度的无量纲增长区末端风速为1.5uref，说明增长区的风速影响上限值受建筑高度影响.

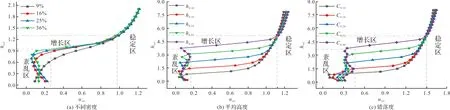
图9 正交平均风速Fig.9 AWV for orthogonal cases

3.3.2 湍动能

同时，对上述建筑形态下城市冠层内的湍动能进行统计分析，如图10所示.其中，图10(a)为不同建筑密度时的正交平均湍动能图，通过分析发现在紊乱区，随着建筑物高度的增加湍动能整体呈减小趋势，且随着建筑密度增大，建筑内部湍动能依次递减，但在0.8倍建筑高度，湍动能出现极最小值.从图中还可发现，当建筑密度小于16%时，增长区湍动能随着建筑高度增加而减少，而当建筑密度大于16%时，湍动能随着建筑高度增加而增加，体现了湍动能在建筑密度为16%时波动较大.图10(b)给出了在建筑密度16%下的不同建筑高度作用下的平均湍动能分布图.图中可以发现，在紊乱区，湍动能随着建筑高度的增加而减少；而在增长区，湍动能在建筑物屋顶附近区域最大，而后随着高度增加而减少，直到稳定区.

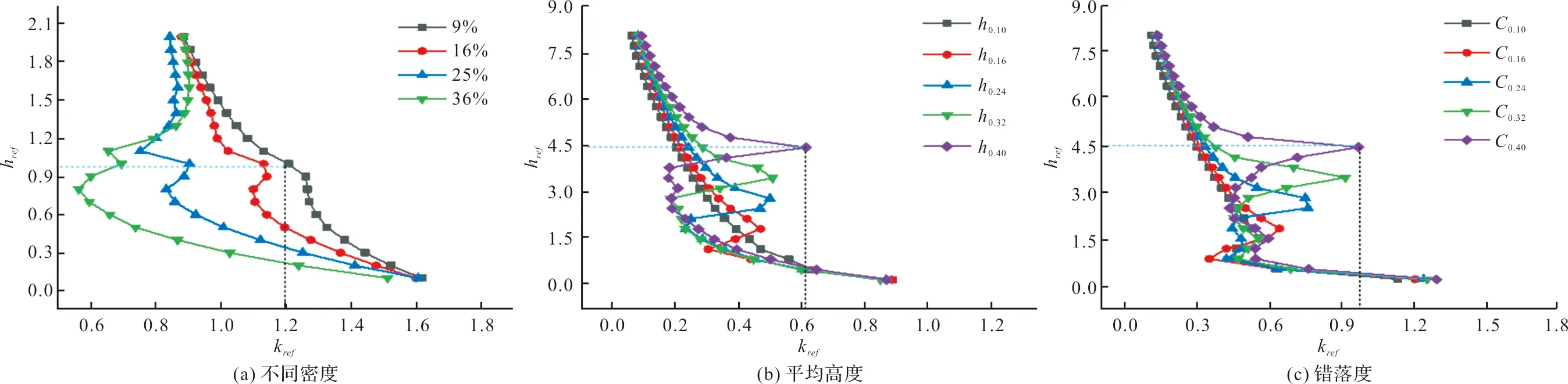
图10 正交平均湍动能Fig.10 Average TKE for orthogonal cases

4 结论

本文采用修正SST自平衡数值模型，对建筑密度、不同高度和错落度3种建筑形态下的城市冠层流场进行了深入分析，探究了不同建筑形态下流场的分布规律，结果表明：

(1)根据建筑物高度，城市冠层风场可分为紊乱区，增长区和稳定区，三者对应的无量纲高度分别为：h1.3href；

(2)冠层内风场在紊乱区风速杂乱无章，平均风速小于规范给定的风剖面风速，错落度和建筑高度可分别提升紊乱区和增长区的上限临界风速；

(3)湍动能在建筑内部大致呈递减趋势，最大值一般出现在建筑物高度位置，对同一建筑密度而言，最大湍动能随着高度有着先减小后增大的规律，对不同错落度而言，湍动能最大值与错落度大小呈正比关系.