圆形高强中空夹层钢管混凝土构件轴压性能试验研究

王灿灿，梁旭东，朱培红，王先铁，庞亚红，孟繁东，吴建灵

(1.国网浙江省电力有限公司 丽水供电公司，浙江 丽水 323000；2.西安建筑科技大学 土木工程学院，陕西 西安 710055;3.丽水正阳电力建设有限公司，浙江 丽水 323000)

钢管混凝土因具有强度高、塑性和韧性好、抗震性能好和施工方便等优点而被广泛应用于桥梁、大跨和高层建筑．目前国内外学者对钢管混凝土构件的力学性能和设计方法开展了较为深入的研究，并且取得了大量成果[1-2]．

钢管混凝土构件在轴心荷载或小偏心荷载作用下具有很好的承压性能，但在构件长细比或荷载偏心距较大时靠近形心处的混凝土承载效率较低，却在增加自重的同时提高了造价，并给基础带来更大的负担．因此，中空夹层钢管混凝土(Concrete Filled Double Skin Steel Tubes，CFDST)构件被国内外研究人员和工程技术人员广泛关注[3]．与实心钢管混凝土构件相比，中空夹层钢管混凝土构件不仅继承了实心钢管混凝土构件承载力高、塑性和韧性好、施工方便等优点，同时具有截面开展、抗弯刚度大、自重轻、经济效益和防火性能好等特点[4-5]．

自20世纪90年代以来，国内外学者对该类构件的力学性能展开了一些研究．Uenaka K等[6-7]以外钢管径厚比和空心率为主要参数对圆中空夹层钢管混凝土短柱进行轴压试验研究，提出了圆中空夹层钢管混凝土构件的轴压承载力计算公式．Zhao X L等[8]对8个不同宽厚比的方中空夹层钢管混凝土构件进行轴压试验，提出了方中空夹层钢管混凝土构件的轴压承载力计算公式．Chen[9]等对7个不同宽厚比的十二边形中空夹层钢管混凝土构件进行纯弯试验，试件均表现出良好的延性．Han L H等[10-11]对28个中空夹层钢管混凝土构件进行循环加载试验，结果表明所有试件均表现出良好的耗能能力，通过有限元和理论分析给出了横向荷载和横向变形之间的关系表达式．Wan C Y等[12]对火灾后圆形中空夹层钢管混凝土构件进行轴压试验，并通过有限元模拟分析了不同温度场对轴压承载力的影响规律，提出了统一温度场下圆形中空夹层钢管混凝土构件的轴压承载力简化计算公式．Li W等[13-14]以含钢率、荷载偏心率和空心率为参数对中空夹层钢管混凝土构件进行受拉试验，采用有限元软件分析了材料强度、含钢率和空心率对构件受拉性能的影响，提出了圆形中空夹层钢管混凝土构件的受拉承载力计算公式．Huang H等[15]进行了12个中空夹层钢管混凝土构件扭转试验，并采用有限元方法分析其受力影响因素，提出了中空夹层钢管混凝土构件的抗扭承载力计算公式．Liang W等[16]以长细比、偏心率和加劲肋形式为参数进行了40个方形中空夹层钢管混凝土试件的受压试验．结果表明，加劲肋能改善试件的延性，但会降低试件整体承载力．这些研究成果为中空夹层钢管混凝土的应用提供了较为充实的理论和试验基础．

综上所述，以往对中空夹层钢管混凝土构件的研究主要集中在对普通强度材料的研究．随着基础设施建设的不断发展，普通强度材料的中空夹层钢管混凝土构件自重大、运输困难、占地面积大等缺点逐渐显现．本文针对圆形高强中空夹层钢管混凝土构件的轴压力学性能开展研究．探究圆形高强中空夹层钢管混凝土构件在轴心受压荷载作用下的受力性能、破坏模式，明确其受力机理，并提出构件的承载力和刚度计算方法．

1 试验概况

1.1 试件设计与制作

设计了6个圆形高强中空夹层钢管混凝土试件，编号分别为CFDST-ZY-1～CFDST-ZY-6．试件高度均为1 500 mm，主要变化参数为混凝土强度、截面空心率χ=Di/(Do-2to)和截面含钢率α=Aso/Ac(Aso为外钢管的横截面面积，Ac为夹层混凝土横截面面积)．钢材设计强度等级为Q690，混凝土设计强度等级为C100和C120．试件主要参数如表1所示．内、外钢管均由两块钢板卷制对接拼焊而成，钢管下端设有20 mm厚Q345钢端板．根据混凝土浇筑时间，共制作四组混凝土试块，编号为C100-1，C100-2，C120-1，C120-2，分别对应试件CFDST-ZY-1～CFDST-ZY-2，CFDST-ZY-3，CFDST-ZY-4，CFDST-ZY-5～CFDST-ZY-6．

表1 试件主要参数Tab.1 Main parameters of specimens

1.2 材料力学性能

按照《钢及钢产品力学性能试验取样位置及试样制备》(GB/T 2975-2018)[17]的要求在不同厚度的钢板上沿纵向切割每组三个标准试样，按《金属材料室温拉伸试验方法》(GB/T 228.1-2010)[18]进行钢材拉伸试验．钢管材性试验结果如表2所示．

表2 钢材材性参数Tab.2 Steel property parameters

混凝土材性试块按照《活性粉末混凝土》(GB/T31387-2015)[19]中的相关要求进行制作和养护，28 d后实测混凝土材性参数如表3所示．

表3 混凝土材性参数Tab.3 Concrete material property parameters

1.3 加载装置与测量方案

试验在20 000 kN电液伺服压剪实验机上进行，试件两端采用单向刀口铰，以模拟两端铰接边界条件．试验加载装置及测点布置分别如图1、2所示，在试件外钢管的中部及两端截面分别布置横向和竖向应变片，以测量钢管的竖向和环向应变．在试件中部对称布置两个位移计，以测量试件中部的横向变形；在试件下端对称设置4个位移计，以测量试件的轴向变形．

图1 试验加载装置Fig.1 Test loading device

在正式加载之前，先预加载2次，加载值约为预估极限荷载的15%．正式加载采用逐级加载制度．在小于60%预估极限荷载范围内，每级荷载取预估极限荷载的10%；当荷载达到60%预估极限荷载后，每级荷载取预估极限荷载的5%．每级加载稳定1 min后记录相应的荷载和应变，接近破坏时慢速连续加载．加载至满足以下2个条件之一时停止加载：荷载下降至85%；试件发生破坏．

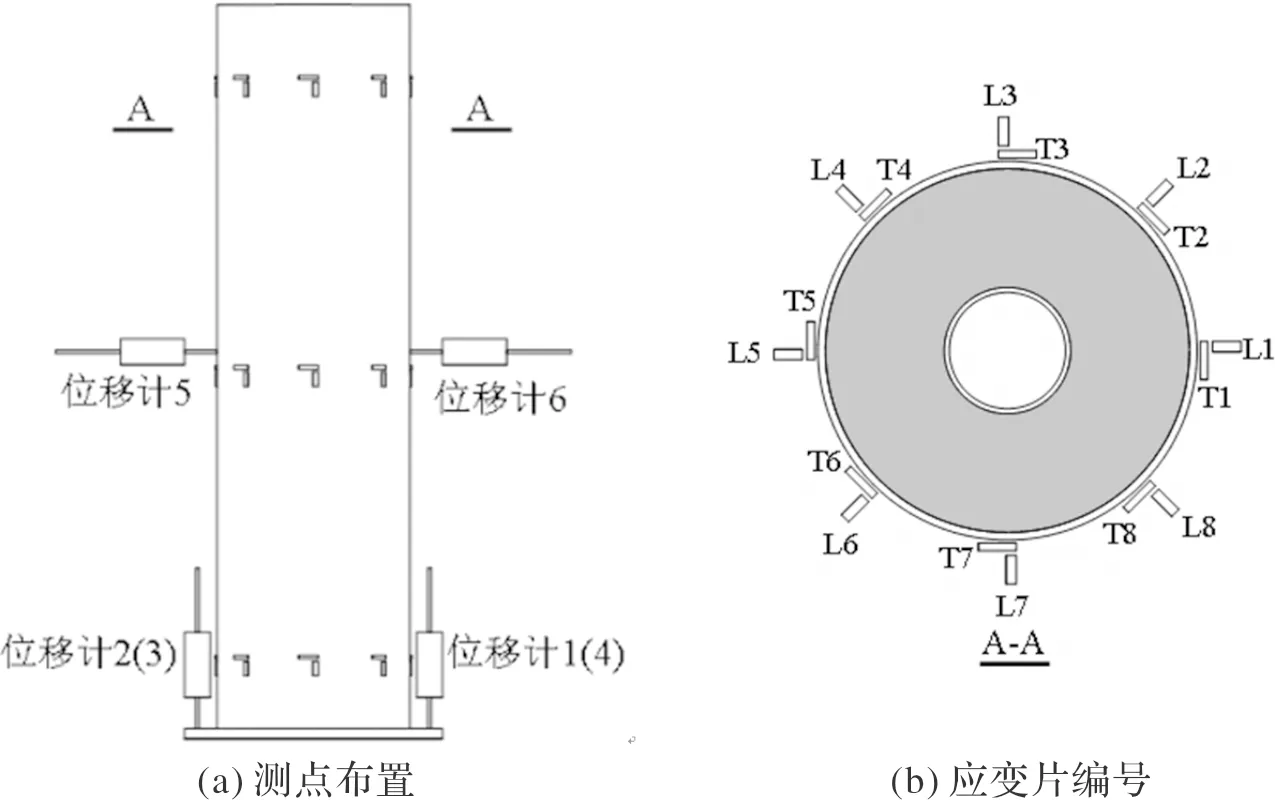
图2 测点布置Fig.2 Layout of measuring points

2 试验结果与分析

2.1 试验现象及破坏模式

试件CFDST-ZY-1～CFDST-ZY-6的破坏过程和破坏模式基本相同．当加载至极限荷载的10%～20%时，试件发出响声，此时外钢管与混凝土脱开．当加载至极限荷载的90%左右时，试件发出巨响，局部混凝土被压碎．但由于钢管的约束作用，试件承载力继续增长，此时外钢管局部出现轻微鼓曲．加载至极限荷载时，外钢管鼓曲愈加明显．继续加载，试件承载力缓慢下降，试件中部和端部均出现不同程度的局部鼓曲，试件发生“鼓曲型”破坏．图3为试件CFDST-ZY-1的破坏形态，试件顶部和中部靠下位置均发生明显的鼓曲如图3(a)；切开外钢管发现核心混凝土整体保持完整，但局部被压碎外鼓如图3(b)；内钢管出现向内的褶皱，其位置和外钢管鼓曲位置对应如图3(c)．由此可见，“鼓曲型”破坏试件在整个加载过程中内、外钢管和混凝土能够协同变形，共同受力．

图3 试件CFDST-ZY-1破坏形态Fig.3 Failure patterns of CFDST-ZY-1 specimen

试件CFDST-ZY-5在整个加载过程中未出现明显的局部鼓曲，而是试件中下部的整体鼓曲，外钢管有明显的斜向剪切线如图4(a)，切开外钢管发现核心混凝土仍然保持为整体，但是出现了明显的斜向裂缝如图4(b)；内钢管出现向内的褶皱，其位置与外钢管鼓曲位置对应如图4(c)，试件发生“剪切型”破坏．

图4 试件CFDST-ZY-5破坏形态Fig.4 Failure patterns of CFDST-ZY-5 specimen

出现这两种不同的破坏形式，其原因与混凝土强度等级和约束效应系数有关．当混凝土强度等级较低时，混凝土脆性相对较小，试件进入弹塑性阶段后，混凝土横向变形增长较为缓慢，约束效应系数较大，钢管对混凝土的约束较大，所以试件发生“鼓曲型”破坏．随着混凝土强度等级的提高，混凝土脆性增大，试件进入弹塑性阶段后，混凝土横向变形急剧增长，当约束效应系数较大时，钢管能够对混凝土提供充分的约束，试件发生“鼓曲型”破坏；当约束效应较小时，钢管不能为混凝土提供足够的约束而发生“剪切型”破坏．所有轴压试件的破坏形态如图5所示．

图5 试验试件破坏形态Fig.5 Failure patterns of test specimens

试件CFDST-ZY-1整体发生了弯曲，分析该试件的荷载-位移曲线可知，试件在达到极限状态以后，承载力下降缓慢，具有良好的延性，而发生失稳破坏的构件在达到极限状态以后，承载力下降较快，构件延性较差．对比长径比相同的两个试件CFDST-ZY-1和CFDST-ZY-4，试件CFDST-ZY-4未出现整体弯曲现象，同时由参数分析可得，该类构件长径比为8时破坏形态为强度破坏，长径比为12时其破坏形态由强度破坏转为失稳破坏．综合以上分析，判断试件CFDST-ZY-1为强度破坏，其发生整体弯曲的原因可能是试件上表面不平整，当试件局部鼓曲后，由于上表面不平整，随着加载继续，试件将向发生局部鼓曲一侧弯曲，最终导致试件出现了整体弯曲现象．

2.2 荷载-位移曲线

图6为所有轴压试件的荷载-位移曲线．加载初期，荷载与位移呈线性关系；当加载至极限荷载的70%～85%时，外钢管部分进入塑性，试件进入弹塑性阶段，抗压刚度不断减小；继续加载，荷载增长缓慢而竖向位移快速增长，达到极限状态后荷载开始下降．除试件CFDST-ZY-5外，其余试件的荷载-位移曲线下降均比较平缓，试件具有较高的后期承载力以及良好的延性．试件CFDSY-ZY-5承载力下降较快、延性相对较差，这与其核心混凝土产生较大的斜向裂缝有关．由图6可知，试件承载力和刚度随着含钢率的增大而减小．这是因为当外钢管尺寸相同时，含钢率的增大使核心混凝土的面积减小，虽然内钢管的面积有所增大，但内钢管提供的承载力增加部分小于混凝土承载力减小部分，所以试件整体承载力减小．当内钢管尺寸相同时，含钢率的增大会减小整个试件的截面尺寸，所以承载力降低．当外钢管尺寸相同时，随着空心率的增大混凝土面积减小，试件承载力和刚度降低．当内钢管尺寸相同时，试件承载力和刚度随空心率的增大而减小．试件承载力随着混凝土强度的提高而提高．

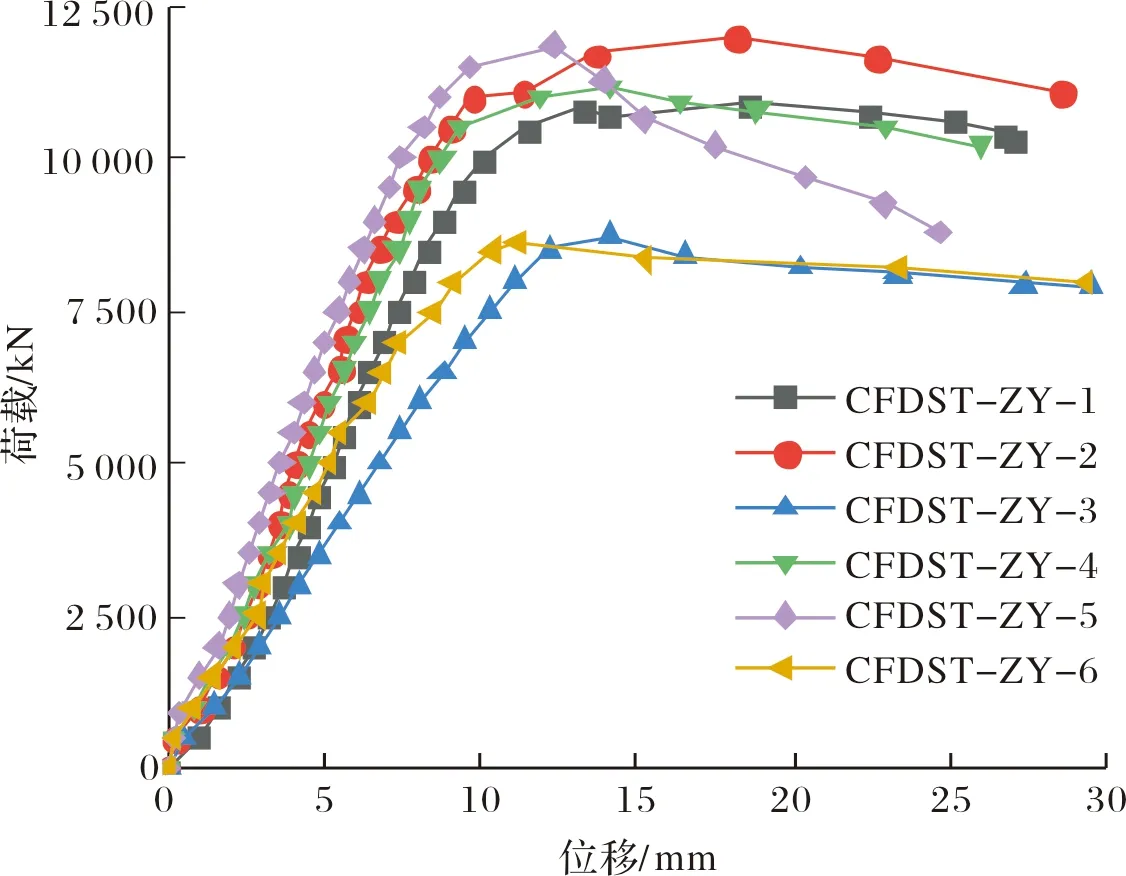
图6 荷载-位移曲线Fig.6 Load-displacement curves

2.3 荷载-应变曲线

图7、8分别给出了“鼓曲型”破坏试件CFDST-ZY-1和“剪切型”破坏试件CFDST-ZY-5的荷载-应变曲线．ε表示应变，下标“T”和“L”分别表示横向和竖向，其中拉应变为正，压应变为负．第一个数字标号“1、2、3”分别表示试件的上、中、下截面．后面的数字表示应变片编号．由材性试验结果可知，外钢管屈服应变为0.003 75．

图7为试件CFDST-ZY-1的荷载-应变曲线．加载初期，试件处于弹性阶段，应变随荷载线性增长；加载至6 037 kN左右时，钢管顶部开始屈服，钢管中部和底部仍处于弹性阶段；加载至8 558 kN时，钢管底部开始屈服；加载至极限荷载时，由于钢管发生局部鼓曲，应变增长速率增大；荷载下降阶段，钢管所有测点均达到屈服应变．越靠近顶部试件的应变越大．

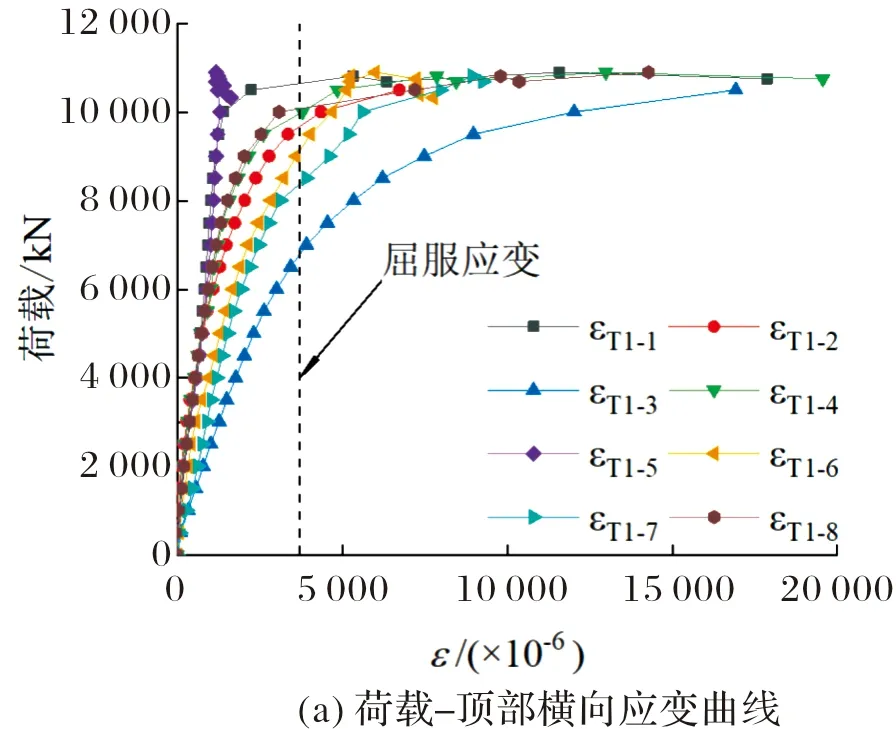
图7 试件CFDST-ZY-1荷载-应变曲线Fig.7 Load-strain curves of CFDST-ZY-1 specimen

图8为试件CFDST-ZY-5的荷载-应变曲线．加载初期，试件处于弹性阶段，应变随荷载线性增长；加载至3 056 kN左右时，钢管顶部开始屈服，钢管中部和底部仍处于弹性阶段；加载至9 550 kN时，钢管底部开始屈服；加载至极限荷载时，由于钢管底部发生整体鼓曲，应变增长速率增大，外钢管底部所有测点均达到屈服应变，而此时钢管顶部和中部截面部分测点仍处于弹性阶段；荷载下降阶段，剪切线通过的地方应变快速增长，其余测点应变增长较慢，甚至部分测点应变减小．

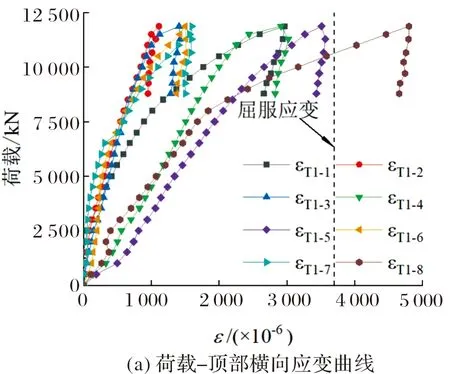
图8 试件CFDST-ZY-5荷载-应变曲线Fig.8 Load-strain curves of CFDST-ZY-5 specimen

由以上应变发展可知，当试件发生“鼓曲型”破坏时，试件整体应变较大，加载后期所有测点均达到屈服应变，试件变形能力得到充分发展，承载力下降较慢，试件表现出良好的塑性性能和良好的延性．当试件发生“剪切型”破坏时，除破坏部位的竖向和横向应变较大外其余部分的应变均比较小，甚至某些截面还处于弹性阶段．由于剪切裂缝的出现使得剪切部位的应变迅速增长，变形急剧增加，而试件其余部分变形不能得到很好的发展，所以试件承载力下降较快、延性相对较低．

3 非线性有限元分析

3.1 材料本构模型

钢材采用双折线模型，受压与受拉的应力-应变关系相同[20]．混凝土材料采用ABAQUS中的损伤塑性模型[21]，混凝土泊松比为0.2，膨胀角为30°，双轴受压强度与单轴受压强度之比为1.16，屈服常数为0.666 7．混凝土采用文献[22]建议的圆钢管混凝土的应力-应变模型．

3.2 有限元模型

采用有限元软件ABAQUS对试件进行非线性有限元分析，钢管和混凝土均采用缩减积分的C3D8R实体单元．为了避免产生“沙漏”现象，在划分部件网格时沿厚度方向至少划分4个单元．钢管和混凝土之间的相互作用采用接触模拟，法向为硬接触，切向为罚摩擦，摩擦系数取0.6．模型底端约束三个方向的平动和X与Z方向的转动，模型顶端约束X与Y方向的平动和X与Z方向的转动，Z方向施加竖向位移．模型网格划分如图9所示．

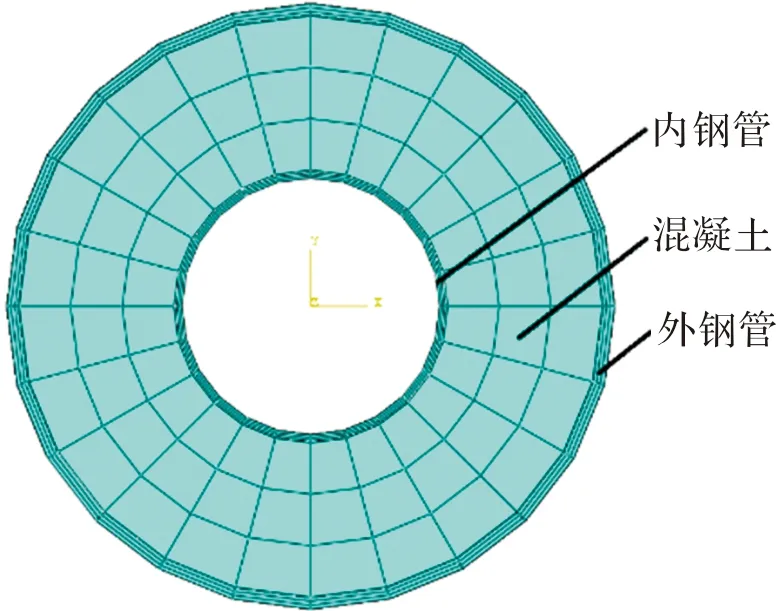
图9 模型网格划分Fig.9 Model meshing

3.3 有限元与试验结果对比

非线性有限元分析得到的荷载-位移曲线和破坏形态与试验得到的荷载-位移曲线和破坏形态对比如图10、11所示．由于有限元分析中加载方式和边界条件为理想状态，而试验过程中包含试件在内的试验系统存在误差和接触间隙．因此有限元模拟的试件初始刚度比试验值略高．但极限承载力和后期刚度吻合较好．由图10、11可知，有限元分析能够较好地模拟试件的轴压受力过程．

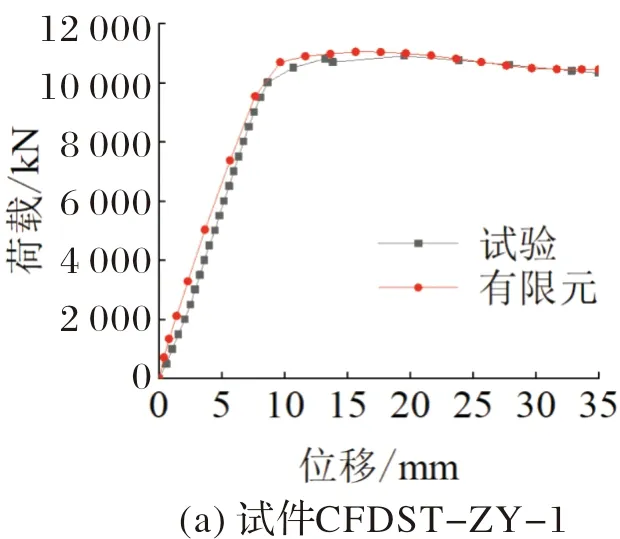
图10 有限元与试验荷载-位移曲线对比Fig.10 Comparison of load-displacement curves between FEM and test

3.4 内、外钢管及混凝土的受力过程

图12为有限元分析得到的试件CFDST-ZY-1的荷载-位移曲线．图中包括试件总荷载、内钢管承担的荷载、外钢管承担的荷载及混凝土承担的荷载．图中有三个特征点，即A点为外钢管开始屈服的特征点、B点为构件达到极限荷载的特征点、C点为纵向平均应变达到0.02[23]的特征点．结合试验与有限元分析结果可知，圆形高强中空夹层钢管混凝土构件在轴压荷载作用下经历以下三个阶段：

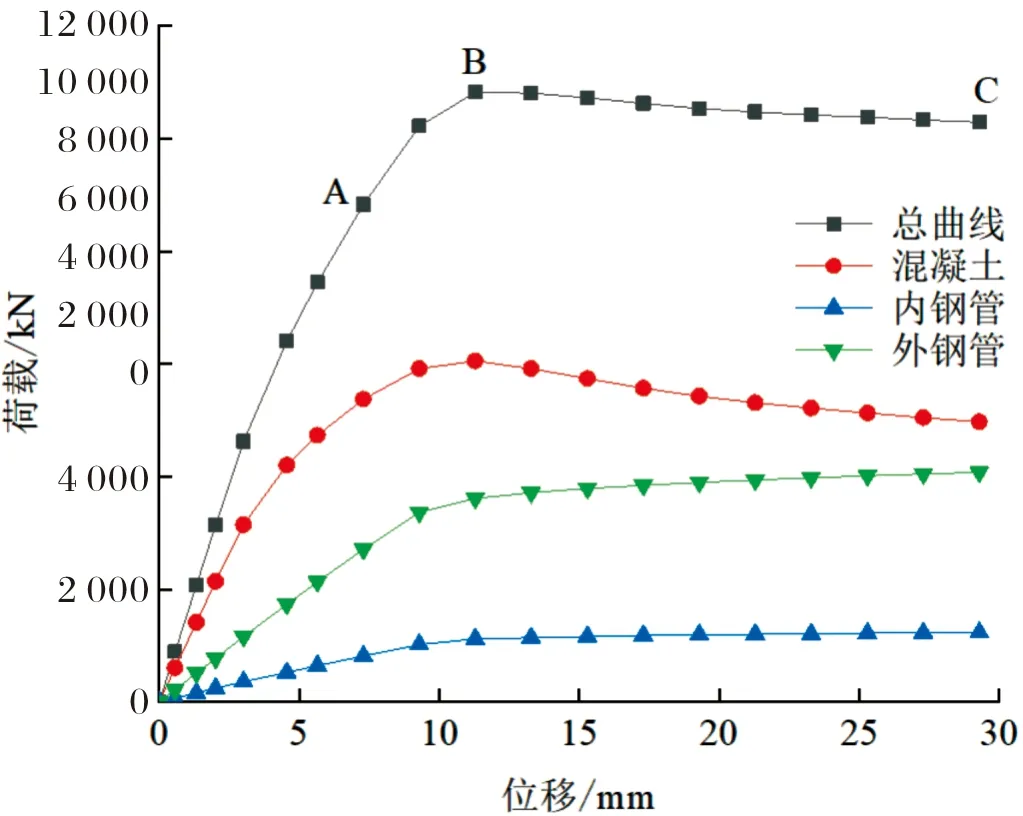
图12 试件CFDST-ZY-1荷载-位移曲线Fig.12 Load displacement curve of CFDST-ZY-1 specimen

(1)弹性阶段，从O点到A点．在此阶段，主要由夹层混凝土与外钢管承受荷载，内钢管承受荷载较小，A点前试件无明显变形，荷载到达A点后，外钢管开始屈服．

(2)弹塑性阶段，从A点到B点．在这一阶段，外钢管屈服，夹层混凝土变形被外钢管约束，混凝土的抗压强度进一步提高，构件承载力继续上升．构件在B点达到极限承载力．

图11 有限元与试验破坏形态对比Fig.11 Comparison of failure modes between FEM and test

(3)下降阶段，从B点到C点．在此阶段，外钢管在底部和中部发生不同程度的向外鼓曲变形，夹层混凝土被压碎．内钢管在底部和中部发生向内褶皱，其他部位无明显变形．

其余各试件的荷载-位移曲线发展趋势基本一致，均包含弹性阶段、弹塑性阶段和下降阶段．只是各部分承担的荷载会随含钢率、空心率和混凝土强度的不同而有所差异．当外钢管尺寸相同时，随着含钢率和空心率的增大，混凝土面积减小，内钢管面积增大，混凝土承担的荷载减小而内钢管承担的荷载增大；当内钢管尺寸相同时，随着含钢率和空心率的增大，混凝土和外钢管面积减小，承担的荷载随之减小．随着混凝土强度的提高，混凝土承担的荷载增大．

3.5 内、外钢管与混凝土之间的相互作用

图13为试件达到极限承载力时，内、外钢管与夹层混凝土之间的相互作用沿构件高度的变化情况．由图13(a)可知，内钢管与混凝土之间的相互作用力在两端较大，中间为零．因为加载端约束了钢管和混凝土的变形使得内钢管和混凝土之间的接触应力较大．整体来说，当试件达到极限承载力时，内钢管对混凝土的变形没有支撑作用．

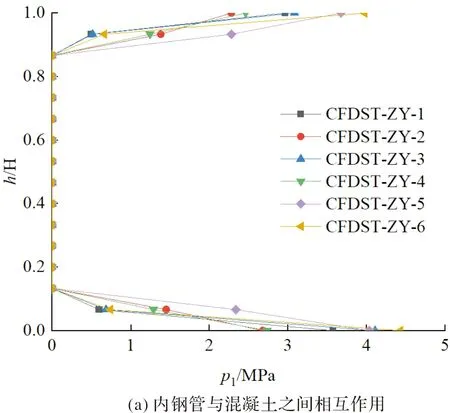
图13 钢管与混凝土之间的相互作用Fig.13 Interaction between steel tube and concrete

由图13(b)可知，外钢管与混凝土之间的相互作用力在两端较小，中间较大．这说明在试件达到极限荷载时，外钢管对混凝土的变形有很大的约束作用．除试件CFDST-ZY-5外，外钢管和混凝之间的相互作用力随着混凝土强度等级的提高而增大，随着含钢率的增大而减小．

4 参数分析

4.1 空心率

图14为空心率为0.54、0.62、0.69、0.77和0.85时，高强中空夹层钢管混凝土构件的荷载-位移曲线．对应的极限承载力分别为112 155 kN、109 473 kN、106 664 kN、103 720 kN和100 286 kN．随着空心率的增大，构件极限承载力减小，空心率的变化对构件轴压刚度几乎没有影响．这是因为随着截面空心率的增大，夹层混凝土承压面积减小，内钢管承压面积增大，但是内钢管面积增大不足以弥补混凝土面积减小带来的承载力损失，所以构件极限承载力减小．

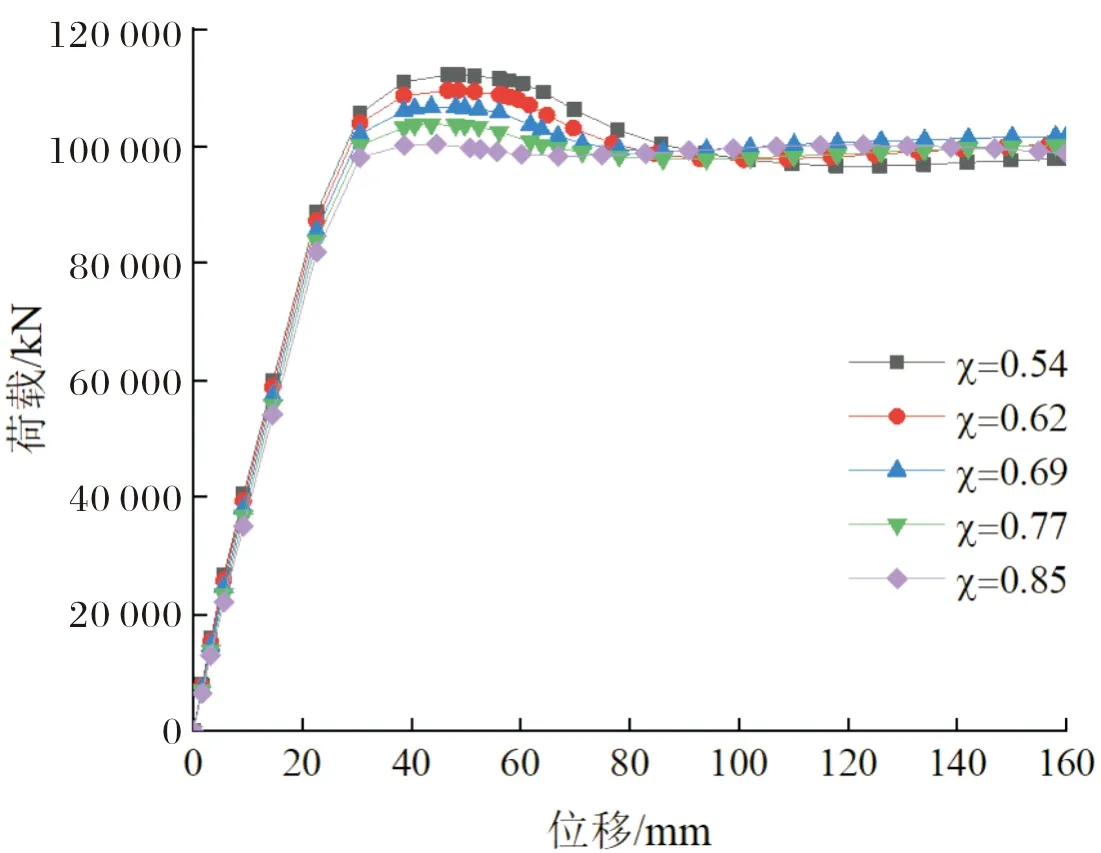
图14 不同空心率构件的荷载-位移曲线Fig.14 Load-displacement curves of components with different void ratio

4.2 混凝土强度

图15为混凝土强度为C60、C70、C80、C90和C100时，高强中空夹层钢管混凝土构件的荷载-位移曲线．对应的极限承载力分别为92 841 kN、96 265 kN、99 154 kN、102 737 kN和106 664 kN．随着混凝土强度等级的提高，构件的极限承载力增大，刚度略有增加．

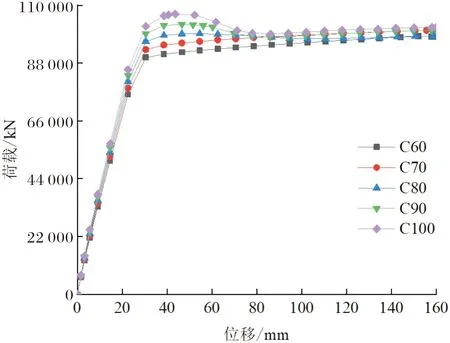
图15 不同混凝土强度构件的荷载-位移曲线Fig.15 Load-displacement curves of different concrete strength members

4.3 内、外钢管径厚比

图16为内管径厚比为30、37、44、51和61时，高强中空夹层钢管混凝土构件的荷载-位移曲线．对应的极限承载力分别为112 112 kN、106 664 kN、102 544 kN、99 756 kN和96 962 kN．随着内钢管径厚比的增大，构件极限承载力和刚度均减小，这是因为内钢管径厚比的增大，内钢管截面面积减小，从而导致其轴压承载力和刚度降低．

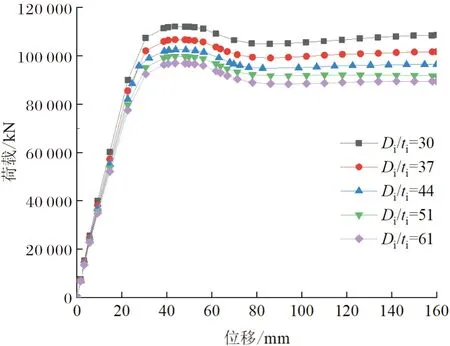
图16 不同内管径厚比构件的荷载-位移曲线Fig.16 Load-displacement curves of members with different inner diameter-thickness ratios

图17为外管径厚比为42、50、55、62和72时，高强中空夹层钢管混凝土构件的荷载-位移曲线．对应的极限承载力分别为115 872 kN、106 664 kN、101 426 kN、97 472 kN和90 544 kN．随着外钢管径厚比的增大，构件的极限承载力和刚度均明显下降．这是因为外钢管径厚比的增大，不仅减小了外钢管的截面面积，而且外钢管对混凝土的约束作用减小，从而导致其承载力和刚度降低．

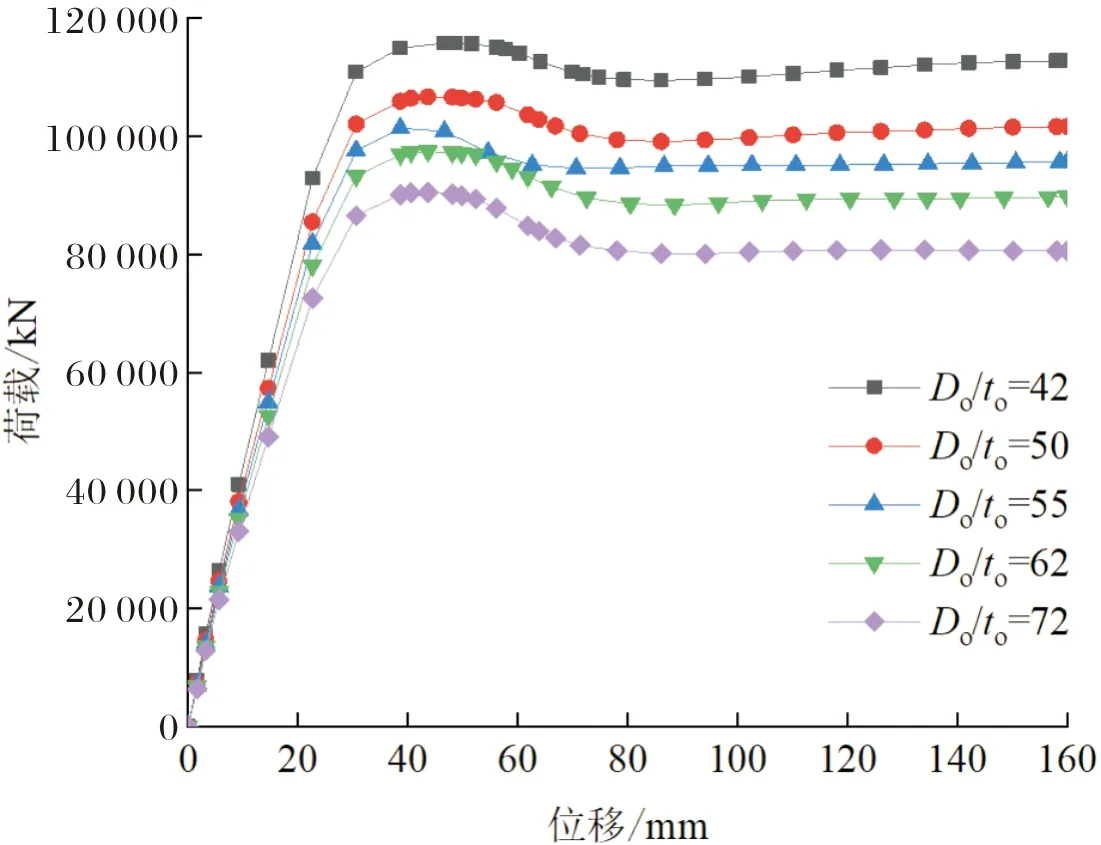
图17 不同外管径厚比构件的荷载-位移曲线Fig.17 Load-displacement curves of members with different outer diameter-thickness ratios

4.4 内钢管强度

图18为内管强度等级为Q460、Q500、Q550、Q620和Q690时，高强中空夹层钢管混凝土构件的荷载-位移曲线．对应的极限承载力分别为98 352 kN、99 798 kN、101 605 kN、104 135 kN和106 664 kN．当内钢管强度从Q460提高到Q690时，其极限承载力提高7.8%，刚度无明显变化．因此，为了降低构件的整体造价，中空夹层钢管混凝土构件的内钢管可以选择比外钢管强度等级低的钢材．

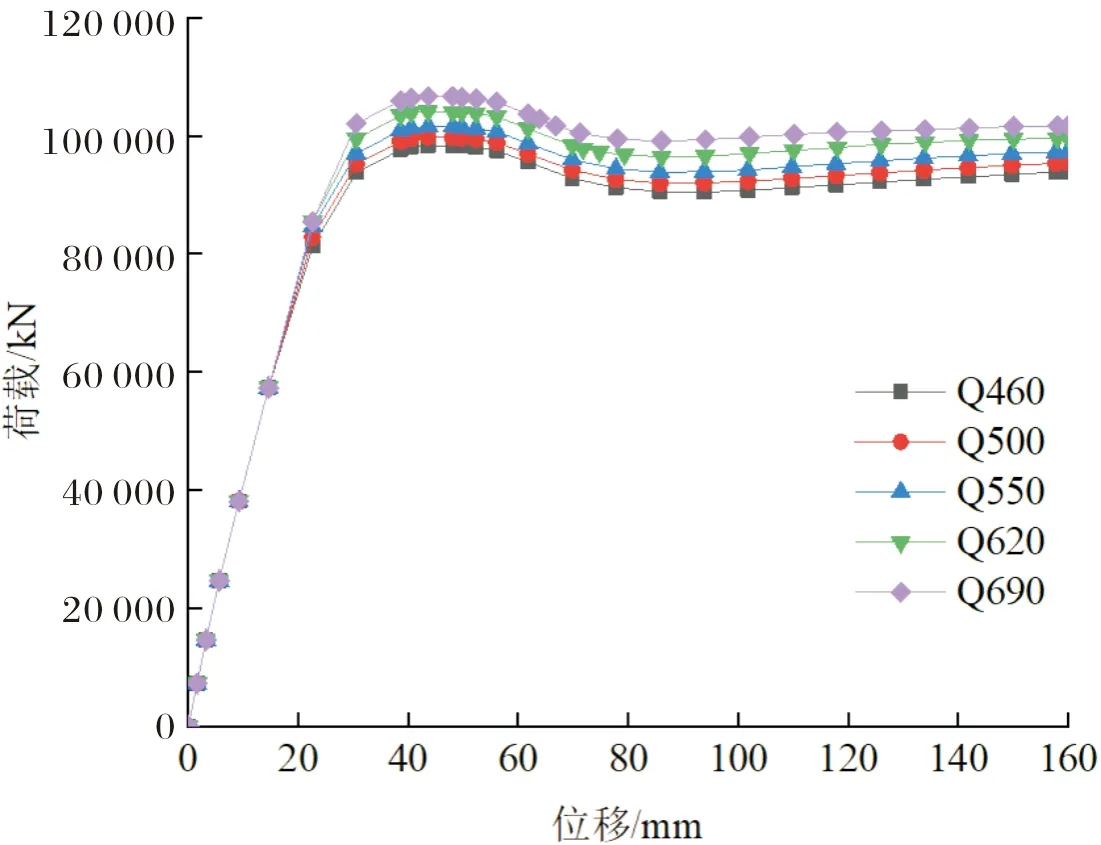
图18 不同内管强度构件的荷载-位移曲线Fig.18 Load-displacement curves of members with different inner steel strength

4.5 长径比

图19为长径比为8、12、16、20和24时，高强中空夹层钢管混凝土构件的荷载-位移曲线．对应的极限承载力分别为106 664 kN、103 547 kN、100 260 kN、99 972 kN和95 096 kN．随着长径比的增加，构件的极限承载力降低，刚度无明显变化．

图19 不同长径比构件的荷载-位移曲线Fig.19 Load-displacement curves of members with different draw ratios

图20为不同长径比的高强中空夹层钢管混凝土构件在轴压荷载作用下的破坏形态．当长径比较小时，构件发生强度破坏如图20(a)所示；当长径比较大时，构件发生整体失稳破坏如图20(b)、20(c)、20(d)和20(e)所示．

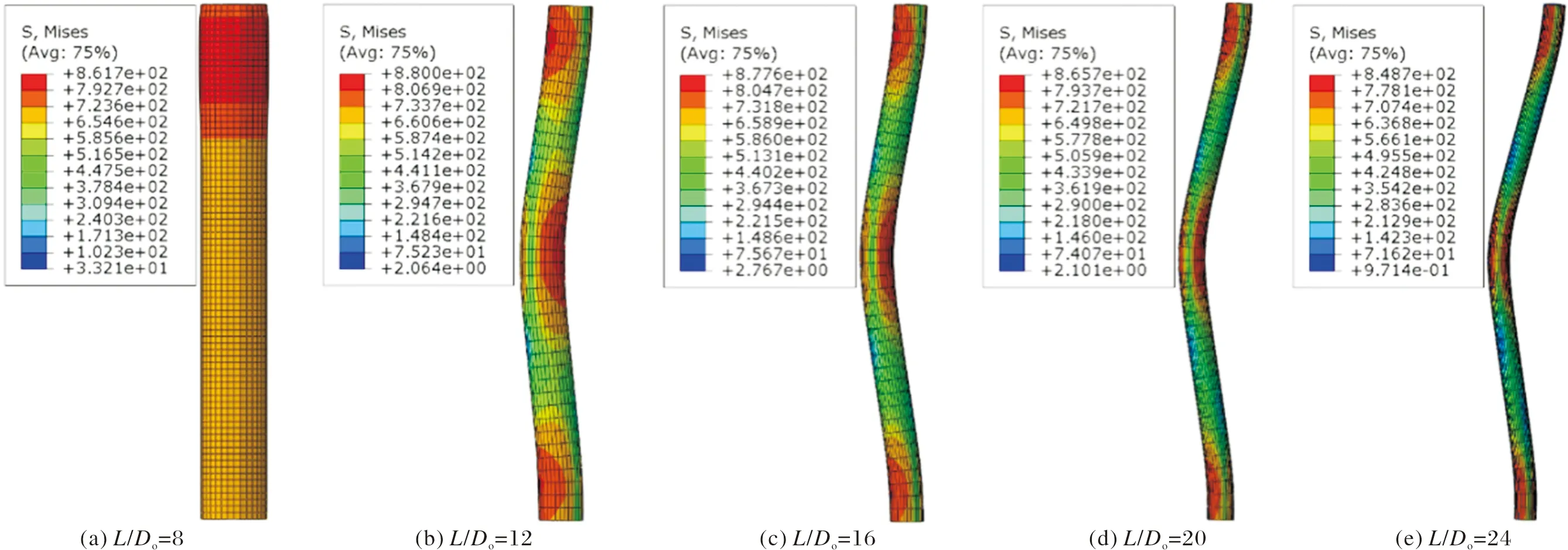
图20 不同长径比构件的破坏形态Fig.20 Failure modes of members with different draw ratios

5 承载力与刚度计算

5.1 承载力计算

T/CEC 185-2018规范(NC)[24]、AISC规范(NA)[25]、EC 4规范(NE)[26]和AIJ[27]规范(NJ)的公式计算结果与试验结果(Nu)对比如表4所示．其中T/CEC 185-2018、AISC和EC 4规范公式计算结果较试验值小，最大误差均超过15%，AIJ规范公式计算结果较试验值大，结果偏于不安全．

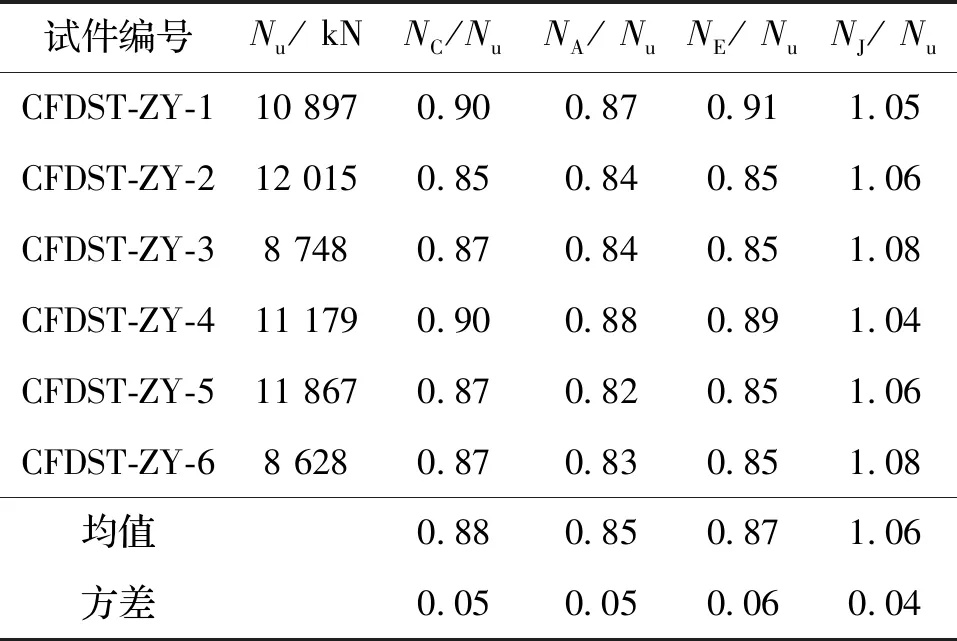
表4 试件承载力对比Tab.4 Comparison of bearing capacity of specimens

T/CEC 185-2018规范与AIJ规范在计算中空夹层钢管混凝土构件的轴压承载力时考虑了钢管与混凝土之间的相互作用，而AISC规范和EC 4规范在计算中空夹层钢管混凝土构件承载力时仅将内、外钢管和混凝土的承载力进行简单叠加，并未考虑钢管与混凝土之间的相互作用．

但中空夹层钢管混凝土构件在实际受力过程当中，达到极限承载力时，由于钢管对混凝土的约束作用使得混凝土的压应力远超其轴心抗压强度．因此在计算中空夹层钢管混凝土构件的轴压承载力时应当考虑外钢管对混凝土强度的增强作用．

本文在T/CEC 185-2018规范轴压承载力计算公式的基础上，进一步考虑钢管对混凝土的约束作用，在原有计算公式的基础上对约束效应系数进行修正．则建议的高强中空夹层钢管混凝土构件的轴压承载力计算公式如下.

Nm=φ·Nm.u

(1)

Nm.u=Nosc.u+Ni.u

(2)

fosc.m=C1·χ2·fo+C2·(1.14+ηξo)·fc

(3)

式中：Nm为轴心受压构件的承载力；Nm,u为轴心受压构件的强度承载力；fosc,m为外钢管和混凝土的组合强度设计值．

由试验结果回归得到高强中空夹层钢管混凝土构件的轴压承载力约束效应修正系数η，结果如表5所示．

表5 约束效应修正系数Tab.5 Amplification coefficient of constraint effect

将η=1.25代入公式(3)中计算各构件的轴压承载力并与试验和有限元结果进行对比，如表6、表7所示．由表可知，建议公式计算结果与试验和有限元结果吻合较好，最大误差为5%．

表6 建议公式计算结果与试验结果对比Tab.6 Comparison between the calculation results of the suggested formula and the test results

表7 建议公式计算结果与有限元结果对比Tab.7 Comparison between the calculation results of the suggested formula and the FEM results

5.2 刚度计算

T/CEC 185-2018规范中给出的中空夹层钢管混凝土构件的组合弹性轴压刚度计算公式为

(EA)sc=Es·(Asi+Aso)+Ec·Ac

(4)

式中：EAsc为组合弹性抗压刚度；Es为钢材的弹性模量；Ec为混凝土的弹性模量；Aso为外钢管的横截面面积；Asi为内钢管的横截面面积．

试验刚度取荷载为0～0.4Nmax的割线刚度[20]．将公式计算值与试验值进行对比，结果如表8所示．

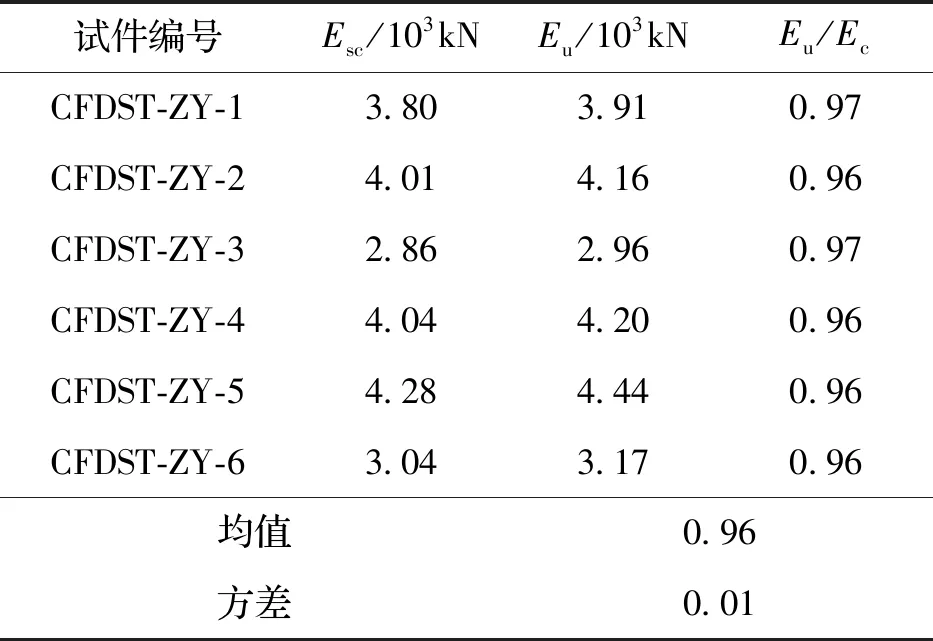
表8 试件刚度计算结果与试验结果比较Tab.8 Comparison between the calculated results of the rigidity of the test pieces and the test results

由上表可知，公式计算结果与试验结果吻合较好．现有中空夹层钢管混凝土构件轴压刚度计算公式能够用于计算圆形高强中空夹层钢管混凝土构件的轴压刚度．

6 结论

通过对6个高强中空夹层钢管混凝土组合构件进行轴压试验，并通过有限元计算和理论分析，得出如下主要结论：

(1)在轴心荷载作用下圆形高强中空夹层钢管混凝土构件可能发生“鼓曲型”破坏或“剪切型”破坏，这与混凝土强度等级和约束效应系数有关．试件发生鼓曲型破坏时具有较高的后期承载力和延性；发生剪切型破坏时延性相对较低；

(2)中空夹层钢管混凝土构件达到极限承载力时外钢管对混凝土的变形有较强的约束作用而内钢管对混凝土的变形几乎没有支撑作用；

(3)随着空心率的增大，构件的极限承载力降低，空心率的变化对轴压刚度影响较小；随着混凝土强度等级的增大，构件的极限承载力和刚度均增大；随着内钢管径厚比的增大，构件承载力和刚度均降低；随着外钢管径厚比的增大，构件的极限承载力和刚度均明显下降；

(4)基于T/CEC 185-2018规范中空夹层钢管混凝土构件轴压承载力计算公式，提出了适用于圆形高强中空夹层钢管混凝土构件的轴压承载力计算公式，公式计算结果与试验和有限元结果吻合较好．T/CEC 185-2018规范关于中空夹层钢管混凝土构件的轴压刚度计算公式能够用于计算圆形高强中空夹层钢管混凝土构件的轴压刚度．