基于离散度多目标粒子群重频组优化算法
2021-08-04周仕霖
周仕霖
(西安科技大学, 西安 710600)
1 引言
雷达脉冲重复频率(pulse repetition frequency,PRF)是雷达波形的一个关键参数,PRF的设计将直接影响雷达的探测性能。工作在中重频模式的雷达通常将不同的PRF组合在一起形成重频组[1],实现解距离模糊和速度模糊,提升雷达波形的抗盲区性能。因此,重频组设计也成为雷达波形优化的重大课题。
雷达重频组可从多个方面进行优化,如解模糊、抗盲区、抗虚影等[2]。传统雷达重频组优化算法是将多目标问题转化为单目标问题求解,而对多目标雷达重频组优化的研究相对较少。如针对解模糊优化问题的重合算法(Coincidence Algorithm)、中国余数定理法[3]、一维集法[4]、滑窗聚类算法[5]及一系列衍生算法[6]等;针对波形盲区问题的遗传算法[7]、模拟退火算法[8]、蚁群算法[9]等,均是解决了雷达重频组的单目标优化问题。这些传统方法虽然具有一定的积极意义,但存在计算速度慢、优化结果受约束值和权重值影响较大的缺点[10];并且,由于传统优化算法寻优能力有限,利用其对多目标雷达重频组进行优化时,不可避免的将多个目标函数主观结合为一个目标函数进行求解,造成目标函数主观性过强,难以保证得到理想的效果[11]。
随着帕累托(Pareto)概念的提出,针对多目标优化问题(multi-objective optimization problem,MOP)相继出现了多种智能优化算法,如非支配排序遗传算法(non-dominated sorting geniting algorithm Ⅱ,NSGA-Ⅱ)[12]、多目标粒子群算法(multi-objective particle swarm optimization, MOPSO)[13]、分布估计算法(estimation of distribution algorithm,EDA)[14]、基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition,MOEA/D)[15]等。但上述算法在对雷达重频组进行优化过程中存在多种问题,如NSGA-Ⅱ存在因交叉和变异随机性过大,导致帕累托前沿(PF)趋近度不够的问题[16];MOPSO存在全局搜索能力较差、收敛速度慢的问题[17];EDA算法模型不够精确,难以处理较为复杂的雷达频率选择问题[18]等,因此,这些算法在对雷达重频组进行优化时,往往达不到理想的效果。
本文针对雷达重频组优化问题,以最小化虚影产生率、最小化盲区、最小虚影为目标综合设计重频组,提出基于改进MOPSO重频组优化算法,求解出雷达重频组的最优pareto前沿,并引入灰色关联度用于折中解的选择,实现了雷达脉冲重频组多性能优化的目标。
2 雷达重频组能力分析
2.1 解模糊能力分析
如果PRF给定,则其最大不模糊距离
(1)
式(1)中,c=3×108m/s为光速常量;fr为PRF的具体数值。最大不模糊速度
(2)
式(2)中:λ为发射波束的波长,此处Vmu为实际值的绝对值。定义波束的不模糊探测空间为Rmu和Vmu,即
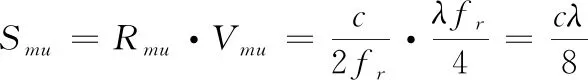
(3)
由式(3)可知:当波束的波长参数确定时,该波束的不模糊探测能力即为定值,Smu在期望的距离和速度探测二维空间上平铺即可得到该波束的探测模糊图,如图1。
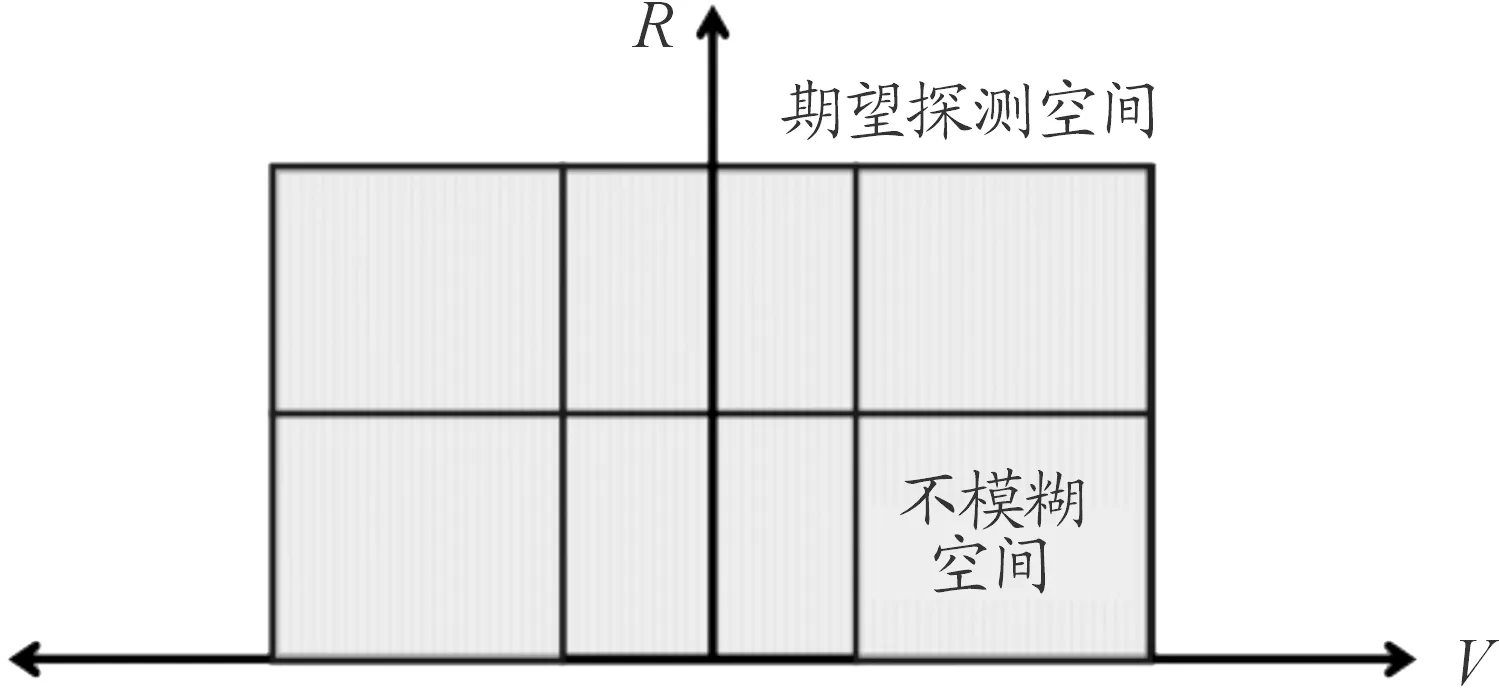
图1 不模糊空间在期望探测空间上平铺示意图
波束重频组设计的首要问题即为期望探测空间的解模糊问题。为了能够解距离模糊和速度模糊,重频组在设计时有两个基础的约束,即

(4)
LCM(PRF1,PRF2,…,PRFM)≥fdmax
(5)
式(4)与式(5)中,LCM为求最小公倍数运算;PRI为脉冲重复间隔(pulse repetition interval),和PRF互为倒数;Rmax为雷达最大探测距离;fdmax为最大多普勒偏移频率;M为解模糊所需最少PRF数目。
N表示重频组中PRF总数目,M和N的设定通常可由M/N准则得到,典型M/N为3/8组合,即8重频组中只要在任意3个重频下检测到目标存在,即上报目标。由此可知在3/8组合下共有56种重频搭配,由式(4)和式(5)可得每种搭配的解模糊距离及解模糊速度。只有当所有搭配的解模糊距离和解模糊速度均大于期望的探测距离和速度时,重频组才能在探测空间内完全解模糊。
2.2 抗盲区性能分析
中重频脉冲在探测时除距离盲区和速度盲区2种主要的探测盲区外,副瓣杂波、杂波、噪声等因素也会造成探测盲区,为了简化计算,仅考虑距离盲区和速度盲区2个主要因素。
由图2可见在距离和速度2个维度上,单重频组成的盲区。由于距离模糊和速度模糊的存在,单重频波束的盲区分别在距离和速度维上延伸,在盲区图上形成网格状分布。当目标处于图2中的黑色区域时,雷达或正在进行脉冲发射,或将接收到的波束频段进行抑制,无法对目标进行有效探测。
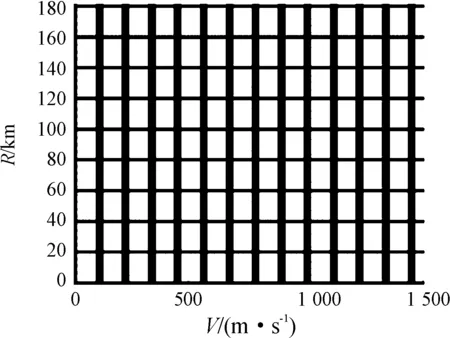
图2 单重频盲区延伸示意图
如图3所示,通过重频组优化,可以大幅减小雷达的距离盲区和速度盲区,大幅提升探测区域内的波束非盲区区域。
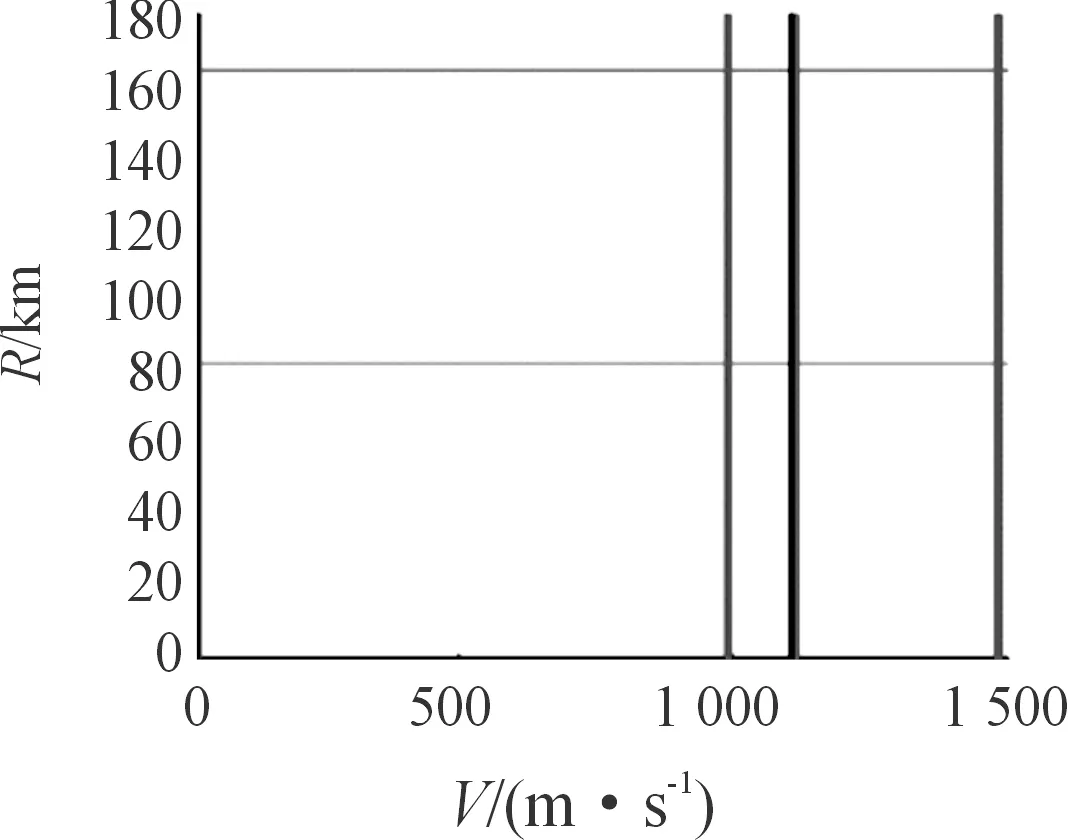
图3 重频组优化后盲区示意图
2.3 抗虚影能力分析
虚影的产生原因主要有2种,一是由于目标的回波在距离单元或速度单元上出现了延伸,跨越了2个或数个单元,以至达到检测门限的回波数量,即达到报告的要求,上报虚假目标;二是对目标的模糊回波在M个PRF下进行了错误的相关,以致在特定的距离或速度上出现虚假目标。
在设计重频组时,保持较大的解模糊余量可以有效减少第1种方式引起的虚影。解模糊余量在探测空间上是波动的,只有在探测空间上的最小解模糊余量满足要求时,才能保证其在所有探测空间上均降低虚影发生的概率。
在保证最小解模糊余量满足要求的前提下,本文主要对第2种虚影问题进行优化。此种方式的虚影产生机制如图4所示,目标1、目标2、目标3的回波在3个PRF中对准,均为真实目标。当不同目标的回波在某一单元内对准时,系统同样上报发现目标,此目标为回波错误相关所致。如果有K个目标,则对参与上述过程的M个PRF而言,能够得到的目标数为,并且这些目标可能分布于M重频的解模糊空间内[19]。
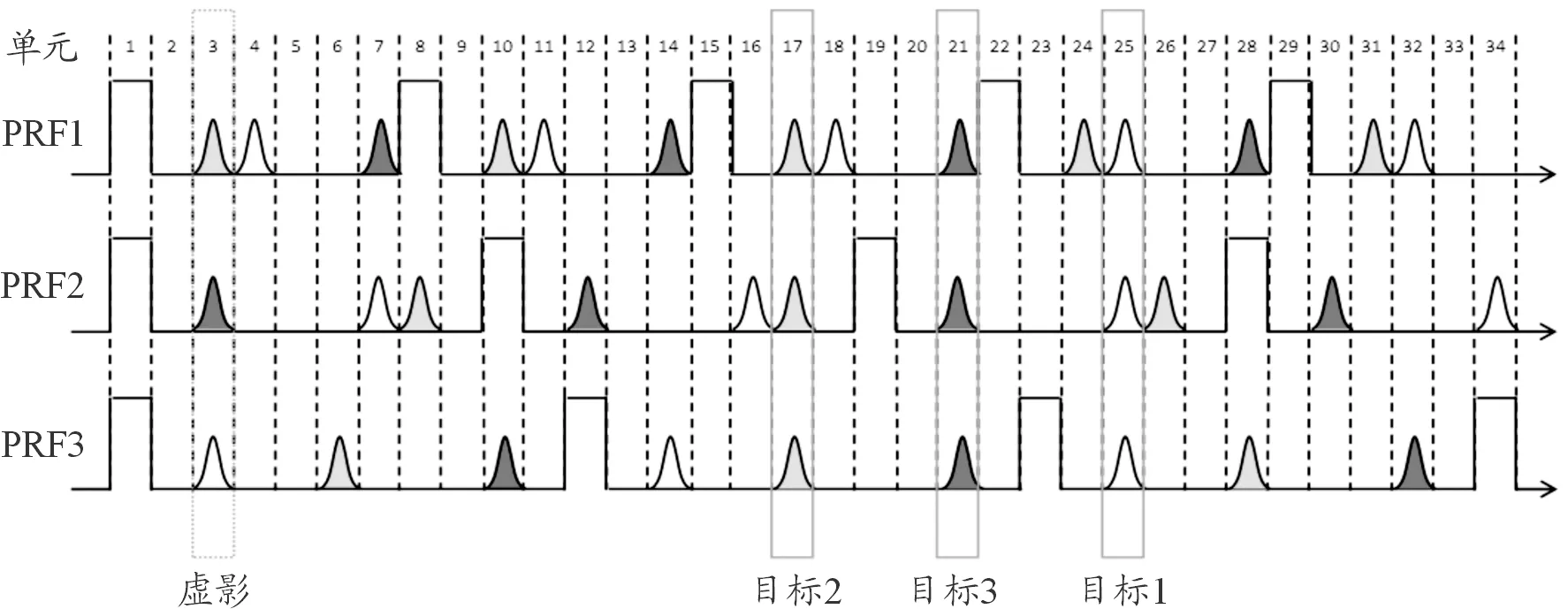
图4 错误互相关产生虚影示意图
如图5所示,当真实目标个数一定时,对于服从3/8准则重频组,得到可能目标数目是确定的KM,然而其最大解模糊空间却不尽相同。在可能目标数目一定的前提下,最大解模糊空间越大,虚影存在于期望探测空间内的概率就越小。因此,为了减少因目标回波错误相关造成的虚影,在保证重频组解模糊余量满足要求的前提下,可以通过扩大重频组对应的最大解模糊空间来降低虚影发生概率。
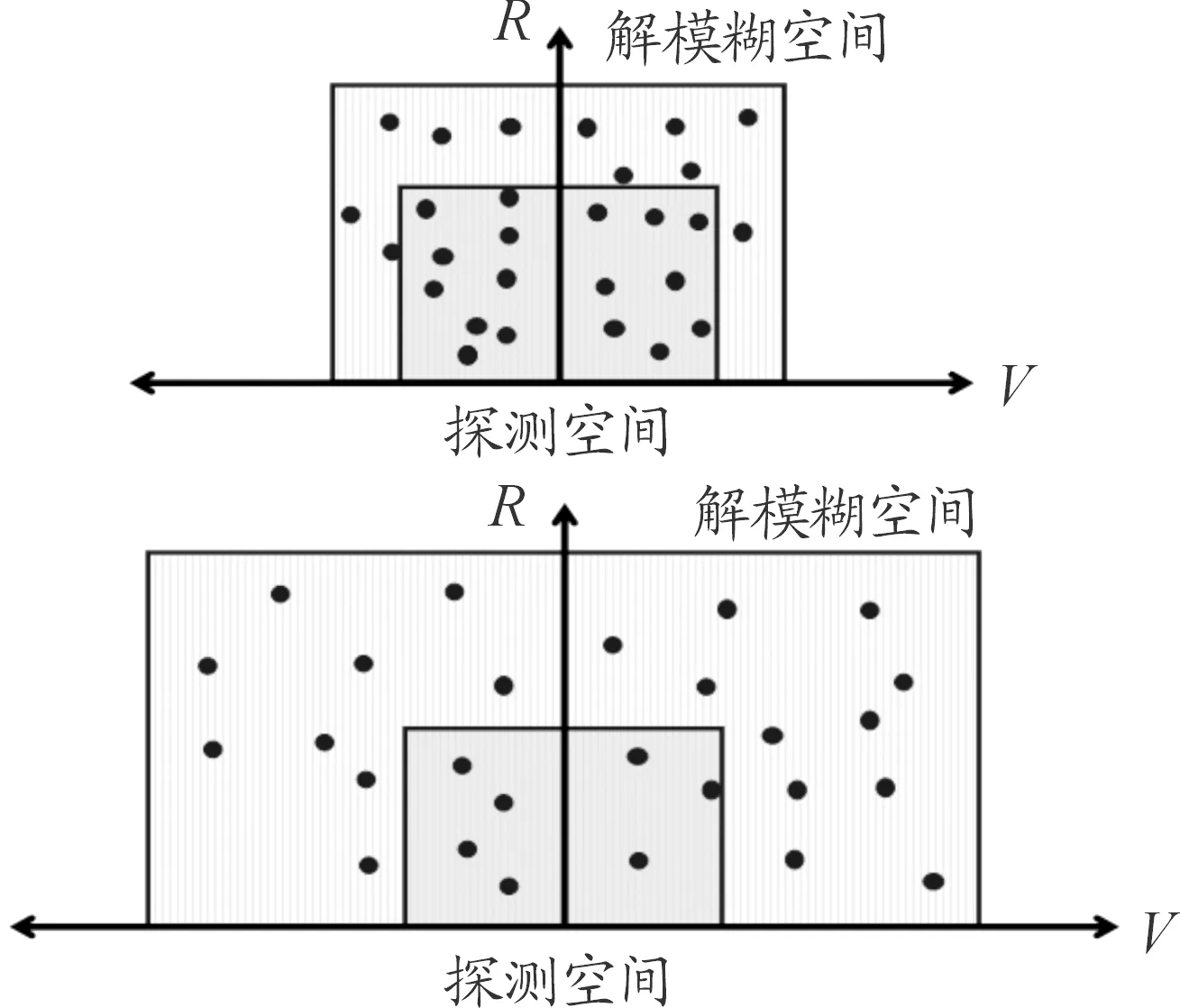
图5 最大解模糊空间对虚影产生概率影响示意图
3 多目标优化模型构建
通过雷达重频组能力分析可知,提升本文重频组优化目标主要为以下2个方面:提高重频组的抗盲区能力,提高在期望探测空间内非盲区区域的比例;扩大重频组最大解模糊空间,降低因回波错误引起的虚影发生率。
为确定在关注区域内,重频组非盲区区域(即可视区域)的占比,即图3中空白部分占全部二维空间的比例。该比例可通过如下过程判定得出:计算重频组内每个PRF的不模糊距离和不模糊速度,并转换为距离单元的个数;根据脉宽和多普勒抑制带宽计算发射遮挡的距离单元和速度单元数;将重频组的不模糊空间按照不模糊距离和不模糊速度为间隔,铺满整个关注探测空间。将关注探测空间根据距离单元和参考速度单元完全划分为网格;在每一个网格上进行盲区判定:判定完所有网格后,将可视网格除以所有关注网格。
R和V分别为重频组的最大解模糊距离和最大解模糊速度,在3/8重频组中,解模糊所需的最少重频数为3个,因此8个重频共有56中组合,每种组合都可通过求解最小公倍数计算(即式(4))得到可以完全解模糊的最大脉冲重复周期(PRI)。通过PRI便能够计算得到最大不模糊距离Rmax,即为R,以及最大不模糊速度Vmax,即V。通过上述方法,便能够计算出Rmax与Vmax的56种组合,则该重频组的最大解模糊距离R和最大解模糊速度V便为这56种组合中Rmax和Vmax的最小值。
式(4)和式(5)给出的是重频组需满足的最低条件,而R和V则是该重频组能够达到的最高条件,如果超过R和V,该重频组将不能解模糊。一般R和V的计算结果非常大,完全能够满足关注探测范围的要求。但是在最大解模糊空间内产生虚影的总数是一定的,如果最大解模糊空间变大,那么虚影落在关注探测空间内的概率就会降低,即虚影发生的概率将会减小。
在对重频组进行多目标优化时,适应度函数的设计将直接影响算法的收敛速度和效果。本文所提算法的适应度函数如式(6):
F=[f1,f2]
(6)
式(6)中,F为粒子适应度;f1=Rdmax、f2=Vdmax分别为该重频组的最大解模糊距离和最大解模糊速度。
PRF的上下限的确定方案有多种,本文选取了较为典型的确定方式。
由于已设定了占空比上限,且脉宽固定,那么PRI的下限即可确定,计算式即为
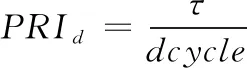
(7)
若PRI小于下限,则占空比将超过20%;PRI的下限与PRF的上限意义相同。
本文多普勒抑制带宽占多普勒带宽的比例选用最为典型的50%占比。多普勒带宽通常为PRF,因此PRF的下限为
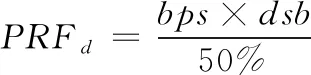
(8)
式(8)中bps为带宽;dsb为多普勒抑制带宽。
通过式(7)与式(8)及PRI与PRF的转换公式,可得PRF的上下限。
4 基于离散度MOPSO算法
本文在传统MOPSO的基础上,通过引入离散度指标,大幅提升MOPSO的全局搜索能力及收敛速度,求解最优的pareto解集,并设置合理求解方法,求出最终的折中解。
4.1 传统MOPSO概述
MOPSO算法是由CarlosA.Coello等在2004年提出来的一种多目标优化算法[20],其通过将pareto思想与PSO算法相结合,将原先只能用于单目标优化的PSO算法扩展到多目标优化上。
MOPSO算法步骤如下[21]:
步骤1:初始化群体和Ak集。
给参数赋初值,生成初始群体P1,并把P1中的非劣解拷贝到Ak集中得到初始非劣解集A1。设当前进化代数为k,在k小于总进化代数时完成步骤1~步骤4的内容。
设当前进化的粒子j,在j小于群体规模时完成1)~3)的内容。
1) 计算Ak集中粒子的密度信息。把目标空间用网格等分成小区域,以每个区域中包含的粒子数作为粒子的密度信息。粒子所在网格中包含的粒子数越多,其密度值越大,反之越小。
步骤3:更新Ak集。
进化得到新一代群体Pt+1后,把Pt+1中的非劣解保存到Ak集中。
步骤4:Ak集的截断操作。
当Ak集中的粒子数超过了规定大小时,需要删除多余的个体以维持稳定的Ak集规模。
结果表明:组成按碳数归类时,采用标准气中n-C4架桥定量和样品气中n-C5架桥定量时,计算的烃露点是一致的,两者相差在0.2℃以内;而中特殊组分单独定量分析时,采用标准气中n-C4架桥定量和样品气中n-C5架桥定量,计算的烃露点也是一致的,两者相差也在0.2℃以内;但采用特殊组分单独定量时,计算的烃露点比组成只按碳数归类时计算的烃露点低,最大偏低值达到6℃左右,说明采用两种数据处理方式获得的组成结果对计算的烃露点有较大影响。
步骤5:输出Ak集中的粒子信息。
4.2 离散度MOPSO算法构建
任何寻优算法寻优的目标就是为了寻找数据空间中的极值点,如图6中A、B、C、D四点。
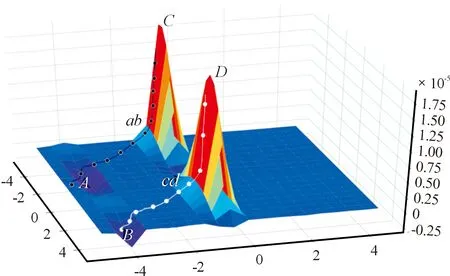
图6 离散度MOPSO算法原理示意图
观察图6可知:若寻优算法采用等步长的搜索方法(ab搜索路径)去寻找最优点时,在数据变化范围较大的极值附近(红色凸起处),由于搜索步长过短,寻优算法需经过多次“无意义”搜索,才能逐渐开始收敛;但在数据变化范围较小的极值附近(蓝色低洼处),由于步长过长,寻优算法无法直接到达极值,许多次在极值附近“徘徊”搜索,造成收敛速度变慢。
基于以上分析,本文通过引入离散度指标,对传统MOPSO算法进行优化。离散度指标表达式如下所示:

(9)
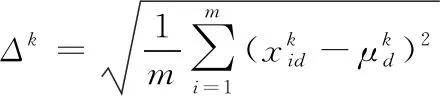
(10)
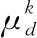
由式(9)和(10)可知:当粒子群的离散程度增大时,其步长也将增加,即当MOPSO算法开始进行寻优或当粒子群处于急剧变化的数据空间时,MOPSO算法寻优速率将会增大,保证算法的寻优效率;当数据空间的离散程度趋于缓和时,MOPSO寻优速率将随之变小,保证算法寻优的精确性。基于离散度改进后得MOPSO迭代式如下:

(11)
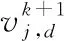
4.3 折中解选择
离散度MOPSO算法虽然能够提供一组解集,但是具体选择哪一种解,还需要决策者根据实际问题进行讨论,本文设计利用TOPSIS[22]对Pareto解集[23]进行排序,其决策过程如下:
1) 对适应度函数矩阵进行归一化处理:
(12)
式(12)中,fi,d为第i个解的第d维空间子目标函数值;ω为解集总数;ai,d为各适应度函数归一化后值。
2) 求“最优解”和“最劣解”:
(13)
(14)
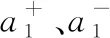
3) 计算各非劣解与A+、A-之间的距离:

(15)
(16)
4) 计算各非劣解与A+和A-之间的贴进度:
(17)
将所求得的Mi按照数字大小进行排序,Mi越大则表示其越接近最优方案。
5 仿真实验
5.1 算法参数设置
为验证本文算法性能,以某一雷达系统为基础,根据其参数进行仿真环境设计。雷达系统的参数如表1所示。通过表1的雷达系统参数数据计算可知,雷达PRI的下限为PRId=τ/dcycle=7/0.2=35 μs,对应PRF的上限为PRFu=1/PRId=28 571 Hz;设定多普勒抑制带宽不超过多普勒带宽的50%[1],则PRF的下限为PRFd=2×1.67×103/0.5=6 667 Hz,对应的PRI的上限为PRIu=1/PRFd=150 μs。
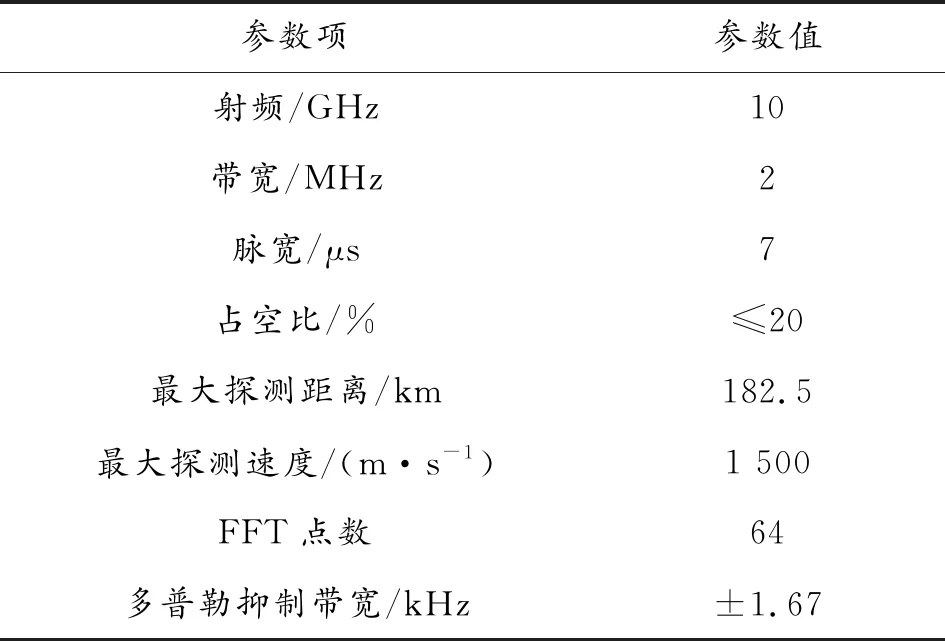
表1 雷达系统参数
根据PRF范围设置算法的初始种群,设定种群数量为50,迭代次数为100,并且w、c1、c2分别设置为0.8、0.5、0.5。同时,仿真设定目标数量为3个。
5.2 仿真结果分析
为了验证离散度MOPSO算法,本文以传统MOPSO作为对比进行多次仿真实验。
1) 2种算法寻优能力分析
图7表示离散度MOPSO算法pareto前沿,其中pareto前沿曲线上黑色圆圈为折中解。由图7可看出本文所提出的离散度MOPSO算法能够依据pareto理论求解出符合雷达重频组多目标优化模型所要求的非劣解集,并依据数据特征,求解其折中解,克服了传统优化算法将多个目标函数人为结合为一个目标函数造成的主观性过强的缺陷。
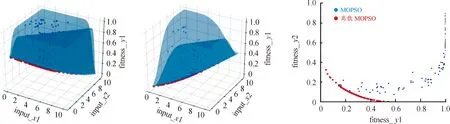
图7 离散度MOPSO算法pareto前沿曲线
图8为根据离散度MOPSO算法与传统MOPSO算法计算得到的pareto前沿曲线。明显可以看出,离散度MOPSO算法pareto前沿曲线明显低于传统MOPSO算法pareto前沿曲线,即离散度MOPSO算法寻优能力、收敛性优于传统MOPSO算法。
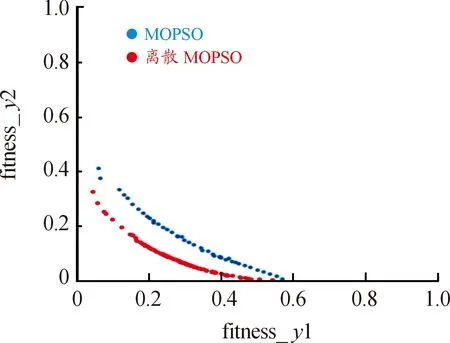
图8 2种算法pareto前沿曲线
2) 雷达重频组优化效果分析
2种算法得到的重频组非盲区区域比例如图9所示。当优化算法为MOPSO时,重频组非盲区区域比例在94%左右,在实验中得到的最高比例为94.32%,而当优化算法为离散MOPSO时,重频组非盲区区域比例在97.5%左右,在实验中得到的最高比例为98.36%。综合来看,本文所提出的离散度MOPSO算法明显优于传统MOPSO算法,且高达97.5%,能较好的减少盲区的比例。2种算法所得重频组在期望探测范围内虚影数目分布如图10所示。由图可知,2种算法在出现虚影数目上存在明显的区别。MOPSO算法得到的重频组虚影数普遍多于离散度MOPSO算法的结果得到的重频组虚影数,即离散度MOPSO算法抗虚影能力优于MOPSO算法。
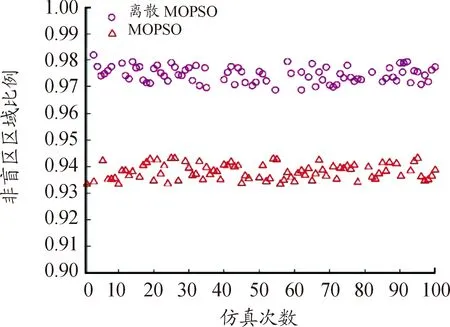
图9 2种算法的非盲区区域比例曲线

图10 2种算法的虚影数目曲线
由图11与图12可知:离散度MOPSO算法所得重频组最大解模糊距离最小值为12 259.170 km,平均值为5 184 788.303 km;最大解模糊速度的最小值为12 259 170 m/s,平均值为 5 184 788 302.635 m/s;传统MOPSO算法最大解模糊距离最小值为4 106.973 km,平均值为2 548 111.957 km;最大解模糊速度最小值为1 134 752.257 m/s,平均值为2 425 804 926.692 m/s。因此,离散度MOPSO算法所得重频组最大解模糊距离和最大解模糊速度值均大于传统MOPSO算法,即离散度MOPSO算法寻优能力更强。
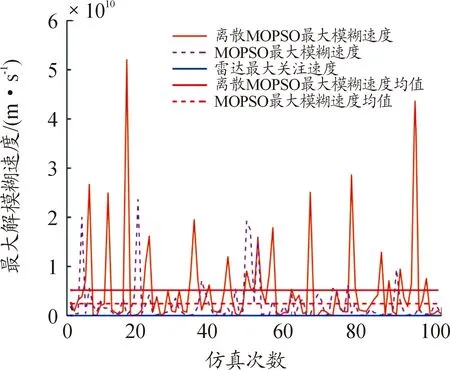
图11 最大解模糊速度曲线
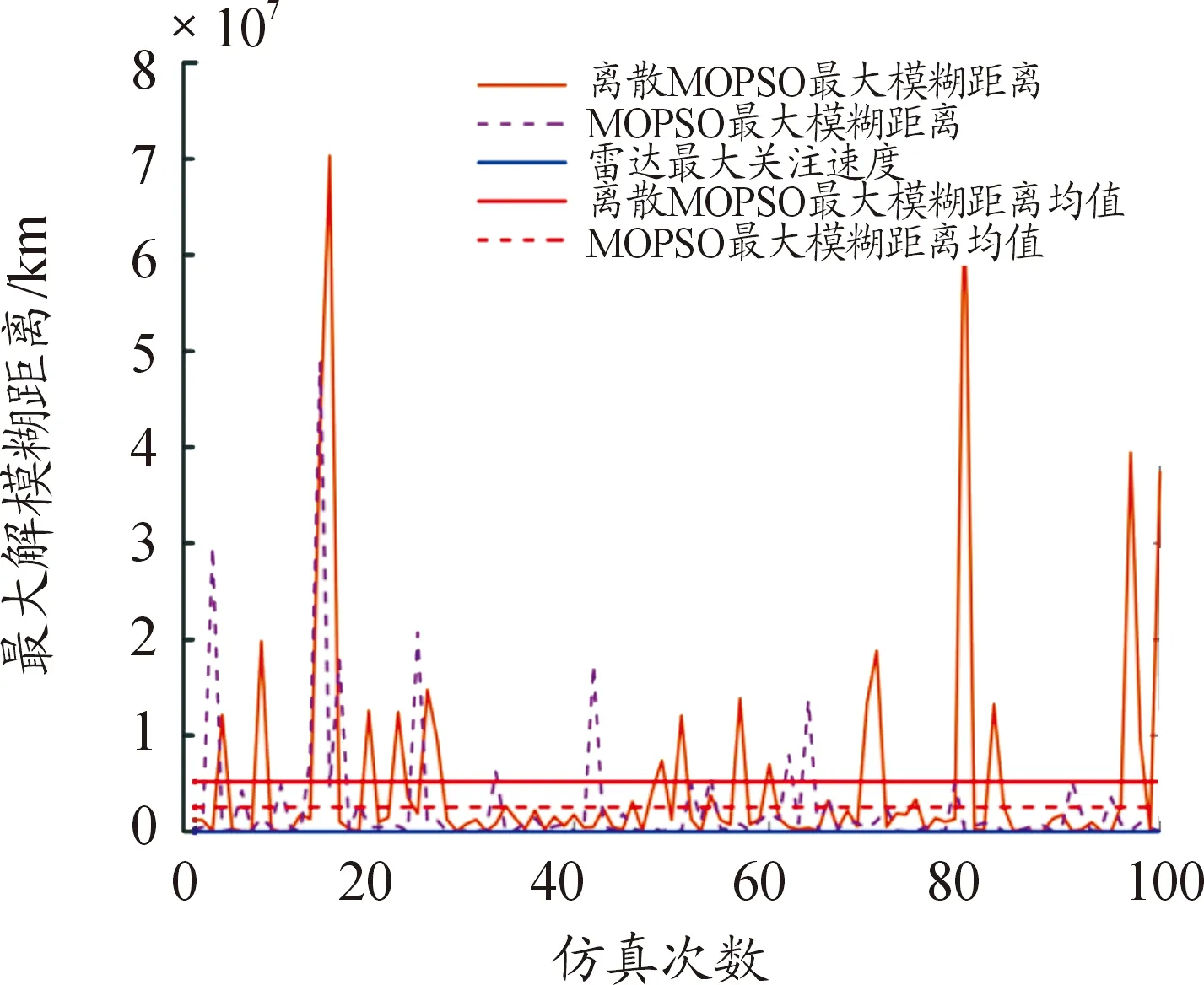
图12 最大解模糊距离曲线
6 结论
针对中重频雷达系统的性能优化问题,提出了一种基于离散度多目标粒子群重频组优化算法。与传统优化算法相比,本文算法克服了主观因素带来的影响;与多目标优化算法相比,本文算法收敛效果好,优化程度明显,但参数选取未实现自适应,有待进一步改进研究。
