基于粒子群算法的自动驾驶仪参数优化
2021-08-04张田田陈志华
张田田, 陈志华, 韩 磊, 贾 芳
(1.南京理工大学 瞬态物理国家重点实验室, 南京 210094; 2.中国兵器工业导航与控制技术研究所,北京 100089; 3.中国兵器第三○四厂,山西 长治 046012)
1 引言
导弹的制导控制系统是实现导弹击毁目标的关键[1]。自动驾驶仪是制导控制系统中至关重要环节[2],确保导弹精确、鲁棒地跟踪制导系统生成的控制指令是它的核心任务[3]。对于新一代近距空空格斗导弹,要求其具有很高的机动性[4-5],要求在保持稳定性的同时快速响应加速度指令,提供大机动性[6-7]。加速度计与质心距离参量c是设计自动驾驶仪需要考虑的重要因素。现有的研究中,对于参量c的处理主要有3种:一是直接忽略它的影响[8];二是对其合理利用[9];三是设计中引用滤波器消除参量c的影响[10]。参量c对于控制输入舵偏、系统响应速度、系统的稳定性都有重要影响,忽略c不仅会导致系统响应慢、稳定裕度低,而且会导致对舵偏需求过高。系统需要的舵偏越大,对舵机的要求就越高,这将在一定程度上影响导弹的控制效果。目前对参量c的研究较少,且未能与粒子群寻优算法设计紧密结合以实现系统整体控制性能最优。
2 基于扩展LQR的自动驾驶仪设计
俯仰自动驾驶仪的设计将被设定为一个LQR最优控制问题,需要对“标准”LQR问题进行扩展,包括目标中的前馈项、输出反馈等。
对于采用轴对称布局的导弹,俯仰和偏航运动方程相似,只有符号正负性不同,所以下面用俯仰通道为例进行研究,其控制方程组可表示为:
(1)

标准的LQR问题不考虑Du项,本文引入Du项设计自动驾驶仪;自动驾驶仪的设计属于LQR跟踪问题,,对于阶跃指令,跟踪问题可转为定点调节问题[11]。
给出状态空间
(2)
式中:ayc、ay分别表示过载指令和输出过载;KDC闭环增益调节系数;V为弹体速度。
H=[Vbδ-caδ-caω],L=[Vbδ-caδ]
以“消除过载误差、减少舵偏输入”为控制目标,建立LQR调节器问题的目标函数
(3)
基于式(3)构造Hamilton函数,并做出以下假设:
假设1:u无约束;
假设2:最优性能指标具有二次型的形式;
参照文献[12]可以得到最优输出反馈控制率u*
u*=-(I+FoptD)-1Fopt(Cx-[KDC0]Tayc
(4)
式中:Fopt为输出反馈矩阵。
为了使系统能够精确跟踪加速度指令,需确定调节系数KDC。
将式(4)代入状态空间(2),根据终值定理
(5)
得到
(6)
式中:
其中“×”表示该矩阵与(I+FoptD)-1Fopt相乘,例L×表示L(I+FoptD)-1Fopt。
3 粒子群算法
3.1 优化目标数学模型
为了提高弹体响应速度、减少舵偏输入、改善阻尼,选用调节时间t、超调量γ、舵偏角δε构成目标函数。其中,调节时间表示系统的响应,超调量表示系统的阻尼[13]。为了保证姿态控制系统的稳定性,一般情况,选取幅值裕度Gm>6 dB,相位裕度Pm>30 rad/s。同时为了简化优化过程,避免参量相互影响,引入权重系数a1、a2、a3将多目标优化转化为单目标优化。图1为优化目标函数图形,用颜色表示第四维函数值f。

图1 优化多目标模型函数图形
(7)
式中:a1、a2、a3分别代表γ、t、δε的权重系数。
3.2 粒子群算法优化流程
文献[14]给出加速度计与质心距离参量c的约束范围,在试验过程中发现,参量c过大会导致实际穿越频率与期望穿越频率偏差过大,参量c偏小会导致系统稳定裕度极低,进而影响系统的稳定性。出于工程上实际应用的考虑,综合弹体结构布局、弹性等多方面因素,本文选取c在[-1,1]的约束范围。
步骤1:采用Matlab指令rands随机生成初始化粒子和粒子速度,种群规模选择50;
步骤2:采用式(7)计算每个粒子的适应度,选取个体的局部最优位置向量Pgj种群的全局最优位置向量Pzj;
步骤3:采用式(8)更新粒子位置和速度;
Vj=Vj+C1rand(Pgj-Xj)+C2rand(Pzj-Xj)
Xj=Xj+0.5Vj
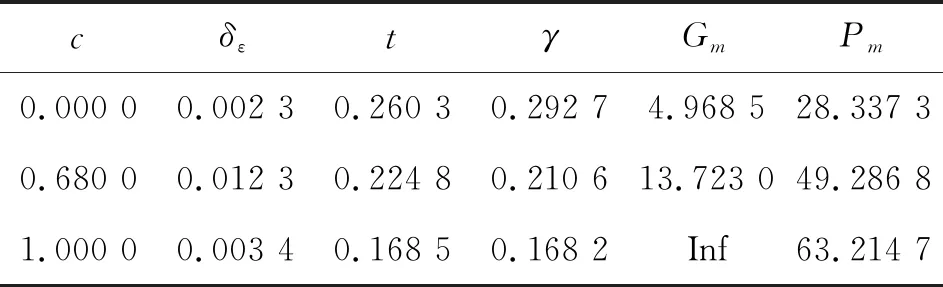
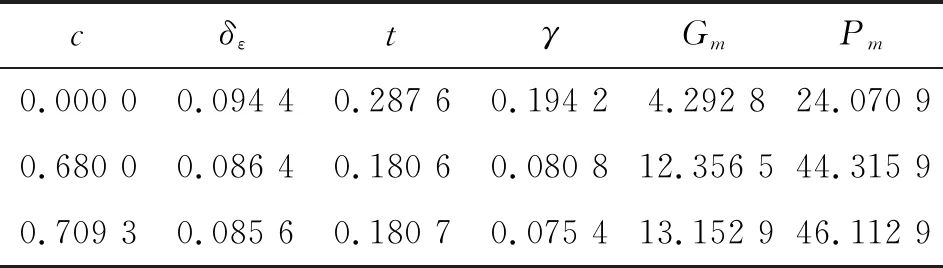
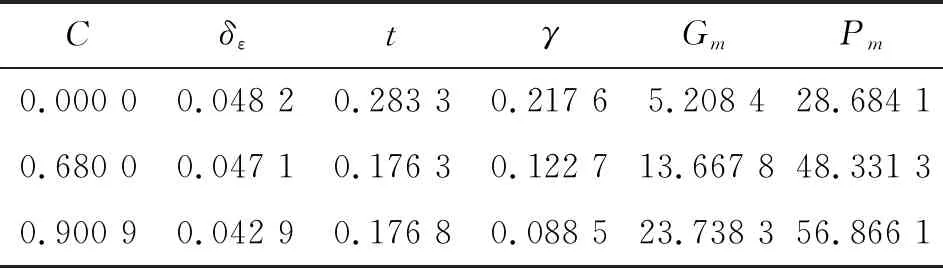
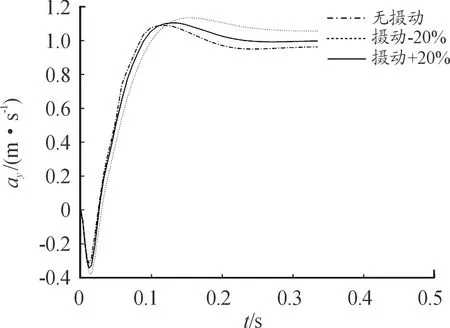
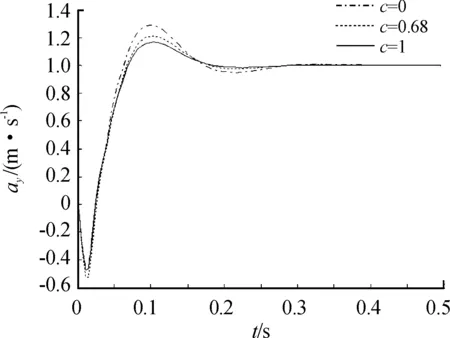
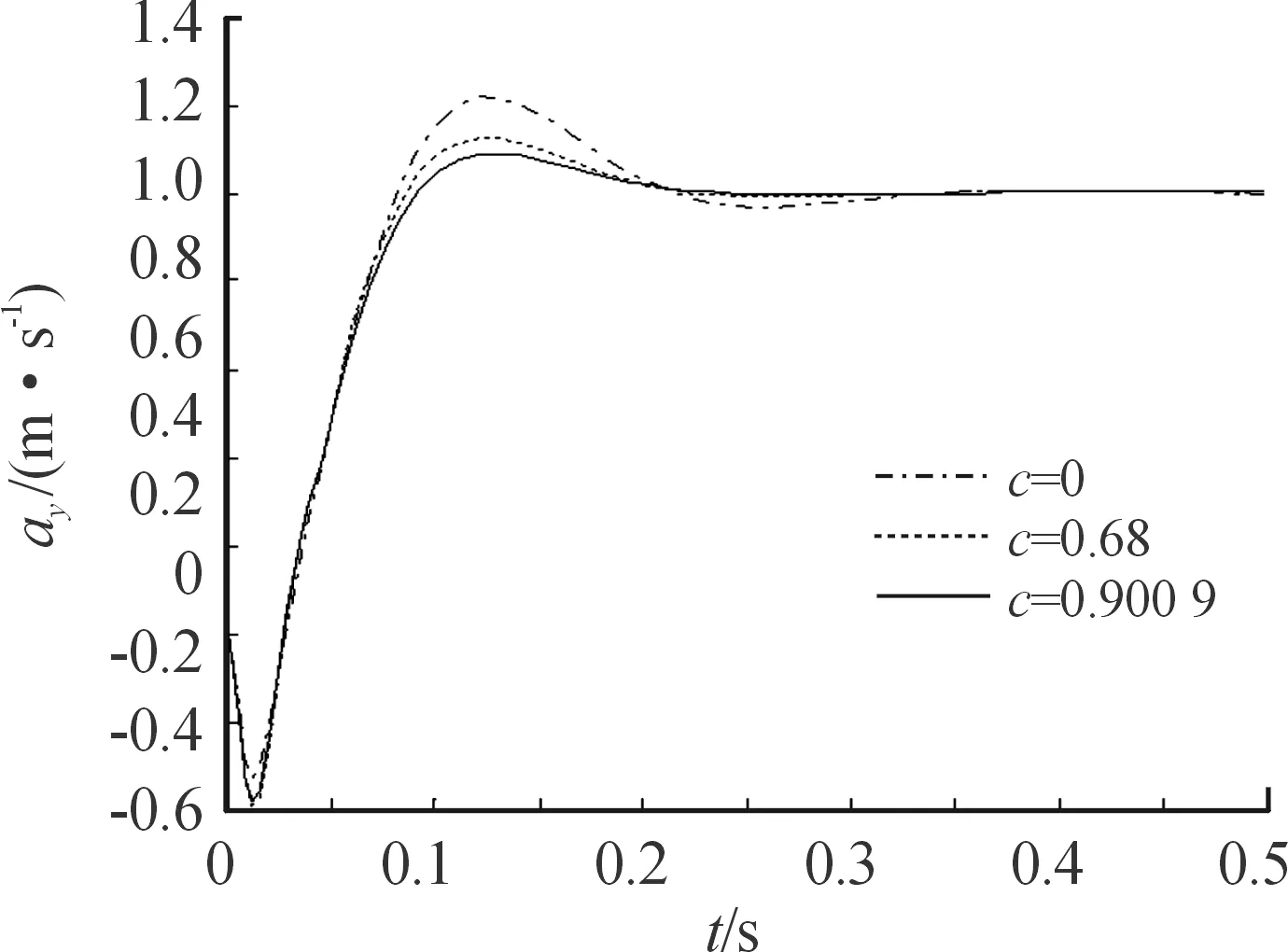
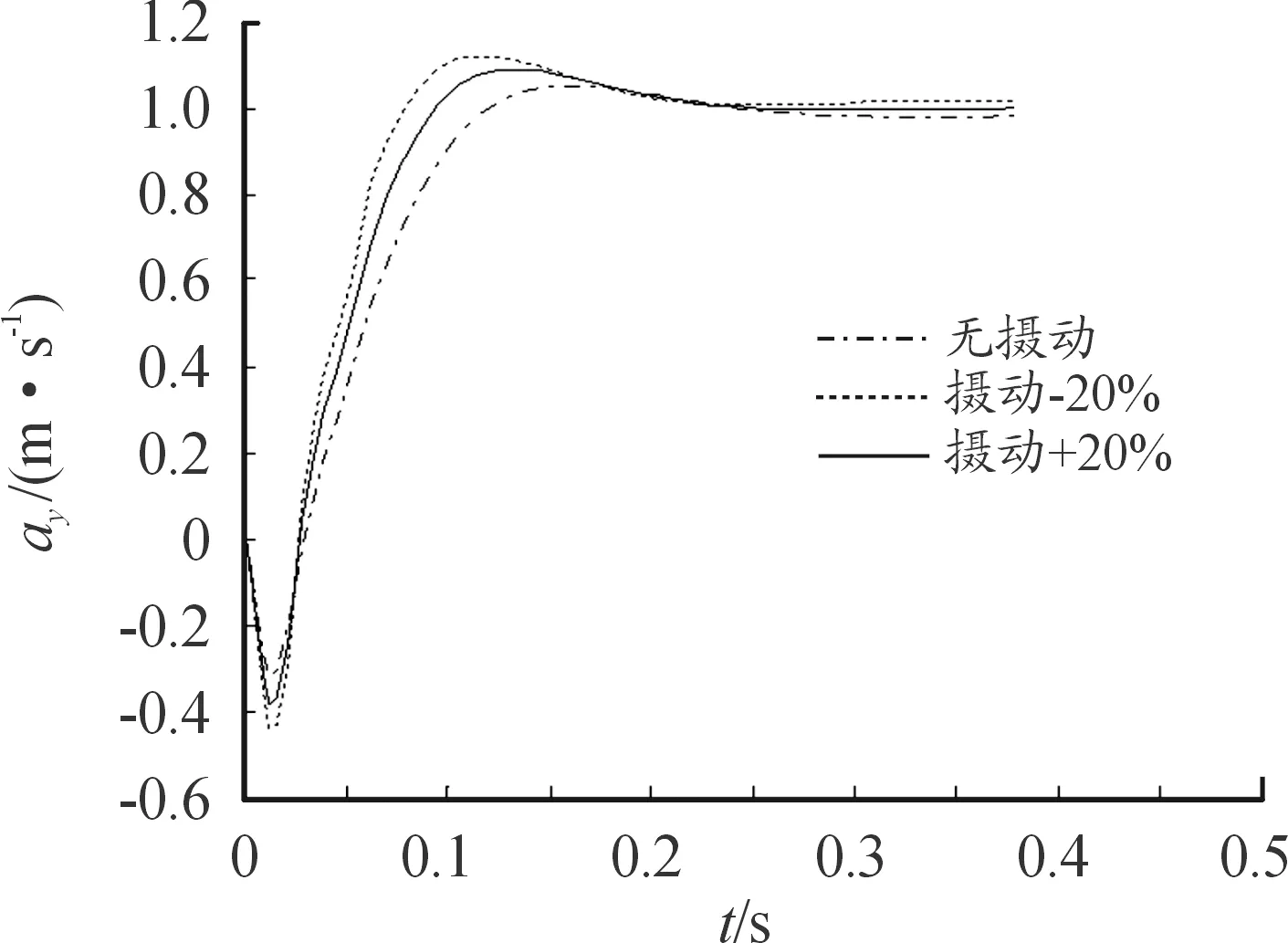
-1 -1 (8) 式中:C1=C2=1.494 45 步骤4:基于步骤3更新的种群,采用式(8)重新计算粒子适应度,判断是否满足终止条件,若不满足,返回步骤2; 步骤5:选取迭代次数为50,当达到迭代次数终止迭代。 图2 粒子群算法优化流程框图 本文以某空空导弹的某一特征点为例进行仿真分析,该特征点动力系数如表1所示。设开环穿越频率为WCR=45 rad/s,舵机频率ω=220 rad/s,阻尼ζ=0.65。静稳定弹体aα=250静中立aα=0静不稳定弹体aα=-250。 表1 特征点动力系数 表2给出LQR加权阵选值,选取恰当的加权阵可以使系统达到期望的WCR。 表2 LQR加权阵选值 补充说明: c=0:表示忽略距离参量; c=0.68:表示距离参量c的一般取值; 下面分别对静稳定弹体、静中立稳定弹体、静不稳定弹体优化结果进行分析。 1) 表3为静稳定弹体的粒子群算法优化结果。c=1,表示优化后的距离参量c的取值。分析表3数据可知,优化后减少72%舵偏角,超调量从21.1%优化到16.8%,调节时间从0.23 s优化到0.17 s。而且稳定裕度也有大幅度的上升,幅值裕度从13.7 dB上升到Inf dB,相角裕度从49 rad/s上升到63 rad/s。 表3 静稳定粒子群优化结果 2) 表4为静不稳定弹体的粒子群算法优化结果。c=0.709 3,表示优化后的距离参量c的取值。分析表4数据可知,优化后减少约为1%舵偏角,超调量从8%下降到7%,调节时间几乎不变。稳定裕度也小福度上升,幅值裕度从12.3 dB上升到13.2 dB,相角裕度从44 rad/s上升到46 rad/s。 表4 静不稳定粒子群优化结果 3) 表5为静中立稳定弹体的粒子群优化结果。c=0.900 9,表示优化后的距离参量c的取值。分析表5数据可知,虽然优化后调节时间有小幅度的上升,从0.176 3 s上升到0.176 8 s,但在超调量,舵偏方面有明显的优化效果。 表5 静中立稳定粒子群优化结果 优化后,超调量从12%优化到8%,舵偏减少8.9%。而且,稳定裕度也有大幅度的上升,幅值裕度从13.6 dB上升到23.7 dB,相角裕度从48 rad/s上升到57 rad/s。 上述分析都是基于优化后距离参量与一般情况c=0.68,可以直观地看出,忽略距离参量c并不是一个很好的选择。事实上,在自动驾驶仪设计中考虑c,即在加速度计测量信息中引入弹体姿态角加速度信息,相当于回路含有一个微分环节,具有超前作用,通常称为加速度计的“杠杆效应”[15]。距离参量c的取值越大,c回路超前作用越明显,系统越稳定,超调越小。 导弹气动参数摄动会引起模型的变化[16],分析基于粒子群设计的自动驾驶仪在气动参数偏差±20%输出响应。 1) 静稳定弹体参数摄动输出响应曲线如图3所示。 图3 静稳定参数摄动输出响应曲线 气动参数摄动+20%,稳态输出偏差4.9%。气动参数摄动-20%,稳态输出偏差5.9%。 2) 静不稳定弹体参数摄动输出响应曲线如图4所示。气动参数摄动+20%,稳态输出偏差3.6%。气动参数摄动-20%,稳态输出偏差6%。 图4 静不稳定参数摄动输出响应曲线 3) 静中立稳定弹体参数摄动输出响应曲线如图8所示。气动参数摄动+20%,稳态输出偏差1.2%。气动参数摄动-20%,稳态输出偏差1.8%。 图3~图8可以看出,优化结果可以快速响应加速度指令,并较好地抑制气动参数变化。 图5 静稳定优化前后输出响应曲线 图6 静不稳定优化前后输出响应曲线 图7 静中立稳定优化前后输出响应曲线 图8 静中立稳定参数摄动输出响应曲线 本文在综合考虑舵偏、稳定性、响应特性等方面的情况下,分析不同加速度计与质心距离参量对驾驶仪性能的影响,并结合粒子群算法寻求到最优距离参量。研究表明,基于粒子群优化算法设计的自动驾驶仪需求更小的舵偏,降低对弹体结构的需求,并在稳定性、响应特性方面也有大幅度提高,能够较好地抑制气动参数变化,在工程上也具有实用性。
4 仿真分析
4.1 特征点仿真分析
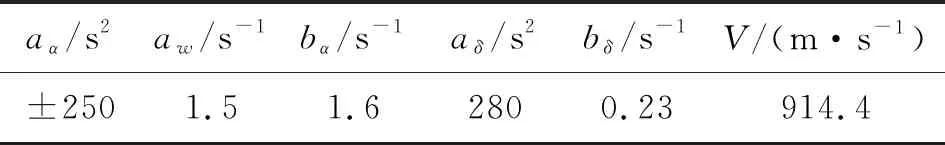

4.2 参数摄动分析


5 结论
