小学高年级数学问题解决教学策略

摘 要：《义务教育数学课程标准（2011年版）》（以下简称《课程标准》）制定了小学数学教学总目标，其中问题解决不仅能很好地巩固学生所学，还可以提高学生运用所学知识解决实际问题的能力，促使学生更好地感受数学知识的应用价值，激发其学习的主动性与积极性。本文对小学高年级数学问题解决教学策略进行了分析，以期给相关教师提供参考。

关键词：小学数学;高年级;问题解决;教学策略

中图分类号：G427                                  文献标识码：A                                    文章编号：2095-9192（2021）19-0014-02

引 言

问题解决涉及的细节较多，如从数学视角发现问题、提出问题、解决问题等。为更好地提升学生的问题解决能力，教师应深入解读《课程标准》的内容，明确问题解决涵盖的内容，做好相关教学内容研究，并积极寻找有针对性的教学策略，从而保证这一教学目标的顺利完成。

一、创设问题情境，提高实践能力

小学数学中有很多知识点与学生日常生活密切相关。因此，在实际教学中，一方面，教师可以鼓励学生进行联想，降低其学习的陌生感，使他们感受到数学知识学习的重要性与趣味性，从而帮助其更好地理解与掌握所学;另一方面，教师可结合自身授课经验及学生需求，创设生活化问题情境，讲解相关知识时将问题展示给学生，并在课堂上留出一定空白，鼓励学生积极动脑进行解答。比如，在教学比例知识时，教师可创设以下生活化情境，以提高学生的实践能力[1]。

例1：某市的居民用电价格为0.52元/千瓦时。为更好地为居民提供供电服务，电力企业推出新的计价方式，鼓励居民自由安装新的电表。新的计价方式分为两部分：在8：00～21：00时段，电价为0.55元/千瓦时;在21：00～8：00时段，电价为0.35元/千瓦时。若你家每月用电在120千瓦时左右，上述两个时间段内的用电量为3∶1，请计算说明哪一种计价方式划算？

该题目以生活化情境为背景，要求学生运用所学知识解决实际问题，既能巩固学生所学，又能促进学生实践能力的提升。该题的难度不大，但解答时学生需要吃透题意。题目要求分析新旧两种计价方式哪一种划算，学生只需计算两种方式的费用即可。使用旧的计价方式不难计算，每月电费=120×0.52=62.4元。新的计价方式需要运用分数或比例知识进行求解，由所学的比例知识可知在8：00～21：00时段所用电量为90千瓦时，在21：00～8：00时段所用电量为30千瓦时，则使用新计价方式，每月电费=90×0.55+30×0.35=49.5+10.5=60元。因为62.4元>60元，显然新的计价方式更为划算。

二、传授解题方法，牢固掌握基本技能

为提升学生的问题解决能力，使学生掌握解题的基本思路，教师要注重对数学题型进行总结，并汇总各种题型的解题方法，如数形结合法、转化法等;要将解题方法融入习题讲解中，提高学生的认知;要鼓励学生进行解题方法的总结，使其在遇到相关的题型时能及时找到解题突破口。为使学生掌握相关解题方法，提高解题的灵活性，教师应结合具体问题，为学生讲解相关解题方法的应用。比如，在讲解“多边形面积”这一内容时，为使学生掌握通法通解，教师可筛选、讲解以下习题。

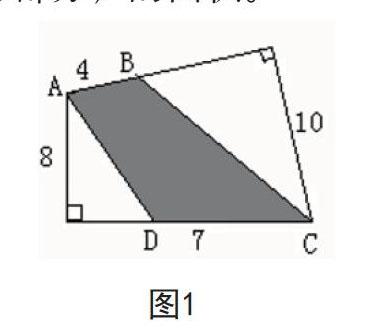
例2：如图1所示的四边形中，其中四条线段的长度已标注在图中（单位：厘米），两个角为直角。求四边形ABCD（阴影部分）的面积。

图1中阴影部分是不规则的四边形，学生无法直接使用学过的规则图形面积计算公式求解。很多学生看到该题目后不知如何下手。事实上，该题目考查了学生灵活运用所学知识解决问题的能力。教学中，为使学生尽快找到解题思路，教师应注重讲解相关的解题方法，即对于求多边形面积的问题可灵活采用添加辅助线法、割补法、平移法等将其转化为规则的几何图形。该题目中的阴影部分是不规则的图形，课堂上教师可引导学生连接AC，将其分割成两个钝角三角形，而后运用三角形面积公式进行计算。其中△ADC的面积S1=×DC×h1，△ABC的面积S2=×AB×h2，分别做DC边、AB边上的高可知，其刚好为已知条件中的8和10，即h1=8，h2=10，由此不难求出四边形的面积S=S1+S2=×7×8+×4×10=48平方厘米。

三、做好创新引导，提高创新意识

为提高学生解决问题的灵活性，教师应引导学生创新解题方法，增强其创新意识。首先，给予学生针对性引导。在实际教学中，教师要做好解题教学安排，选择能够运用多种方法解答的习题，为学生讲解其中一种解法，并积极鼓励学生进行思考，看能否找到其他的解题思路。其次，积极开展一题多解训练活动，让学生尝试找到另外的解题思路，并指名板演解题过程。这不仅能活跃课堂气氛，还能提高学生的创新能力。比如，在讲解方程知识时，教师可以围绕以下习题开展一题多解的训练活动。

例3：某班共有男生26人，在一次考试中共有30人超过85分，则女生中超过85分的人数比男生中未超过85分的多几人？

该题目难度稍大，解题的关键在于找到参数之间的关系。解答该题时，很多学生认为可运用简易方程知识进行求解，即可设女生中超过85分的人数为x，则男生中超过85分的人数为（30-x），而男生中未超过85分的人数为[26-（30-x）]=（x-4），则x-（x-4）=4。课堂上，教师可以给学生留下一定的时间，要求学生进行讨论，鼓励学生思考能否从另外的角度分析。结果一些学生认为可设男生中未超过85分的人数为x，则超过85分的人数为（26-x）。女生中超过85分的人数为30-（26-x）=（x-4），因此，（x-4）-x=4人。两种方法从不同的角度设出未知数，都顺利地得出了正确答案，殊途同归。如此教学不但巩固了学生对方程知识的认识与理解，而且在一定程度上提高了学生的创新意识，使其在解题中能够做到一题多解。

四、鼓励学生合作，养成反思习惯

在小学数学教学中，教师应注重提升学生的合作、交流意识，并使其养成良好的反思习惯，及时发现与弥补解题中的不足，从而促进学生解题能力与解题水平的不断提升。一方面，教师应结合教学内容为学生积极创设合作学习情境;另一方面，教师应引导学生进行解题后的反思，即在学习或解题中，鼓励其多与其他学生交流经验，积极向他人请教，借鉴他人成功的学习与解题方法。在讲解应用题知识时，教师可组织学生围绕以下习题开展小组合作活动。

例4：操场的环形跑道长为400米，甲、乙两位学生先后相距100米（甲在后面），同时出发按逆时针方向跑步，甲、乙两人的速度分别为7米/秒、5米/秒。他们每人跑100米都停5秒，则甲追上乙需要多少秒？

该题目具有一定难度，对学生的理解能力要求较高。为使学生能够顺利求解，教学中教师可将班级学生分为两人一组进行思考解答，以培养学生问题解决中的合作意识。同时，教师要给予学生相互交流的机会，使其积极学习他人的成功经验，反思自己解题的不足，总结出一套适合自己的解题思路，从而使其以后能够更好地解决类似问题。部分学生通过交流认为，为更好地解答该题，可绘制相关的草图辅助分析。通过分析可知，甲乙两位学生每跑一秒，其之间的距离缩短2米，而之前相距100米。假设他们均没有停止，则甲追上乙需要100÷（7-5）=50秒。甲跑100米、200米、300米时各停留了5秒，则甲追上乙共需时间为50+5×3=65秒。

结  语

总之，在小学高年级数学教学中，教师应明确《课程标准》要求，做好问题解决内容的解读，将问题解决教学融入相关教学环节中，尤其做好相关习题的设计，巩固学生所学，使其学习与积累运用数学知识解决问题的技巧與经验，从而不断提高其解题水平与解题能力，进而实现数学学习质量的更好提升。

[参考文献]

陈好.浅析小学高年级数学的解决问题的策略[J].课程教育研究，2020（20）：155.

作者简介：杜莺舞（1978.10-），女，福建厦门人，本科学历，研究方向为小学数学教育教学。