利用GPS和水文负载模型研究云南地区垂向季节性波动变化和构造变形
2021-08-03胡顺强王坦管雅慧杨振宇
胡顺强, 王坦, 管雅慧, 杨振宇*
1 首都师范大学资源环境与旅游学院, 北京 100048 2 中国地震台网中心, 北京 100045
0 引言
GPS技术在地壳运动监测中已经得到了成功的应用(Wang et al., 2001;Gan et al., 2007; Zheng et al., 2017; Wang and Shen, 2020).可靠的GPS垂向速度场主要是通过GPS连续站观测数据解算得到,由于目前GPS连续站较少,且解算得到的垂向位移误差大致是水平方向位移误差的2~3倍以上(Liang et al., 2013),因此,GPS垂向位移在地壳形变中应用较少.GPS垂向位移中除了真实的地壳构造变形之外,还受以周年和半周年的季节性波动变化的影响(Dong et al., 1998; Nikolaidis, 2002; 田云锋和沈正康, 2009).大气、水文及非潮汐海洋等地表质量负载是引起GPS垂向位移中季节性变化的主要原因(Van Dam et al., 1994, 1997; Zerbini et al., 2004; 王敏等, 2005; Wu et al., 2019).在一些陆地水变化较大的区域,水文负载引起的季节性变化能达到厘米级(王林松等, 2014).因此,如何去除GPS垂向位移中因大气、水文及非潮汐海洋负载引起的垂向季节性变化,最大限度地获得真实的地壳构造运动引起的变形量,成为地壳动力学研究的热点(Pan et al., 2018;Zhan et al., 2020; Li et al., 2020).
分析大气、水文和非潮汐海洋等地表质量负载引起的垂向季节性变化方法主要有地表负载模型和GRACE模型等.对大气和非潮汐海洋负载的研究,非潮汐海洋负载对沿海地区的GPS垂向位移改正效果更好(Van Dam et al., 2012).Petrov 和Boy(2004),Tregoning和Van Dam(2005)分别研究了大气负载引起的垂向季节性变化可达20 mm和18 mm.对水文负载的研究,由地表负载模型得到的水文负载形变对GPS垂向季节性变化的影响为毫米到厘米不等,且改正GPS垂向位移后的均方根值都会减少(Van Dam et al., 2001; Dill and Dobslaw, 2013; Xiang et al., 2018).多位学者使用GRACE模型数据所得的水文负载形变和GPS垂向季节性变化进行对比研究,大部分结果表明两者在总体上具有较好的相关性和一致性(Davis et al., 2004;Nahmani et al., 2012;Fu and Freymueller, 2012;Pan et al., 2016;丁一航等, 2018; Li et al., 2019a).Dong等(2002)的研究结果表明大气、水文和非潮汐海洋负载引起的GPS连续站最大周年振幅分别可达4 mm、7~8 mm和2~3 mm,可以解释约为40%的GPS垂向季节性变化.综合上述研究可知,不同地区不同地表质量负载(大气、水文、非潮汐海洋)对GPS垂向季节性变化影响均不一样.
云南地区(21°N—29°N,97°E—106°E)位于青藏高原东南侧,是多块体组成的重要地质研究区,内部具有澜沧江、小江和红河等多条大型且复杂的断裂带,是中国大陆现今构造活动最为剧烈的区域之一(Gao et al., 2017).部分学者分别使用时间跨度在2010—2012年(盛传贞等(2014)) , 2010—2015年(Hao等(2016), Zhan等(2017))的GRACE模型和GPS数据研究云南地区的GPS垂向位移与水文负载形变情况,认为水文负载是引起云南地区GPS垂向运动季节性变化的主要因素之一.然而,GRACE只能有效分辨大约400 km范围内水文负载变化,对于GPS连续站局部小尺度范围的水文负载影响不能有效辨别,因此,本文使用时间跨度更长(2011—2020年)且空间分辨率为0.5°×0.5°的格网LSDM模型和GPS数据来探讨云南地区垂向运动的季节性变化和现今构造变形.前人分析水文负载对云南地区GPS垂向运动的季节性变化影响时,在季节性信号提取方面关注比较少.因此,本文使用奇异谱分析(Singular Spectrum Analysis,SSA)方法提取GPS垂向位移和LSDM形变的季节性信号.由于GPS垂向位移和LSDM形变中含有其他非周年信号且相位差可能随时间变化,传统的皮尔逊相关系数只能简单的从单一时间尺度上衡量两者的相关性,而忽略了两者在多时间尺度上的相关性.小波分析可以分析不同时间序列在不同时段和频率尺度上的相关性,能够揭示两者在时频空间中的相位关系(Xu, 2016).因此,本文使用连续小波变换、交叉小波变换(Cross Wavelet Transform, XWT)和小波相干性在时频空间下多时间尺度研究GPS垂向位移与LSDM形变的周期特性.
1 数据与方法
1.1 GPS数据
本文选取的云南地区27个GPS连续站观测数软件解算得到,首先利用GAMIT进行单日解解算,估计站位置、卫星轨道参数及方差-协方差矩阵等;然后使用GLOBK进行网平差,从而获得连续站的单日解坐标时间序列,详细的解算策略参考文献(Zhao et al., 2015).在对GPS垂向位移进行分析之前需要进行粗差剔除、阶跃改正、缺失数据插值等预处理.预处理主要方法如下:
1)采用四分位距法(Inter Quartile Range, IQR)对GPS垂向位移进行粗差探测和剔除,IQR判别准则原理如下:
IQR=Q2-Q1.
(1)
异常值探测区间为
[Q1-1.5·IQR,Q2+1.5·IQR],
(2)
式(2)中,Q1和Q2分别表示为最靠近1/4和3/4处的下分位值和上分位值.

图1 云南地区27个GPS连续站分布和数据缺失图Fig.1 Location and Data availability of 27 GPS stations in Yunnan region
2)使用最小二乘线性拟合方法对GPS垂向位移的阶跃项进行改正.
3) 使用Schneider (2001)提出的正则期望最大化(Regularized EM, RegEM)方法对云南地区27个连续站的GPS垂向位移中缺失的数据进行插值,该方法顾及了27个GPS连续站之间的相关性和物理背景,不需要先验信息和依赖数据模型,只根据数据自身特性进行插值,在GPS坐标时间序列插值中已经得到了广泛应用(明锋, 2019; Li et al., 2019b).其主要原理如下:
由p个连续站和m个观测天数的GPS垂向位移组成m×p维矩阵X,对于矩阵X中的任一个连续站的GPS垂向位移,非缺失与缺失的GPS垂向位移可使用线性回归模型来描述:
xm=um+(xa-ua)B+e,
(3)
式(3)中,矩阵B∈Rpa×pm为回归系数,残差e的均值为0,协方差阵C∈Rpa×pm为未知的随机变量,非缺失与缺失的GPS垂向位移组成的向量分别为xa和xm,均值分别为ua和um.给定的均值u和协方差阵通过条件最大似然估计法计算X中每一行包含数据缺失的GPS垂向位移的回归系数B和残差协方差阵C,然后再使用式(4)对缺失的GPS垂向位移进行插值.
(4)
图2为KMIN、XIAG、YNMH和YNTC连续站经过预处理后的GPS垂向位移,从图2中可看出使用RegEM方法的插值效果与整体运动趋势一致.

图2 预处理后的KMIN (a)、XIAG (b)、YNMH (c)和YNTC (d)连续站的GPS垂向位移Fig.2 The GPS vertical displacement of KMIN (a),XIAG (b),YNMH (c) and YNTC (d) stations after pretreatment
1.2 地表负载模型数据
地表负载模型使用德国波斯坦地学中心提供的由于大气负载、水文负载和非潮汐海洋负载形变的规则全球格网数据(Dill and Dobslaw, 2013),空间分辨率为0.5°×0.5°.其中,水文负载形变由时间分辨率24 h的LSDM模型数据(Dill, 2008)计算得到,大气和非潮汐海洋负载形变分别由时间分辨率3 h的ECMWF模型和MPIOM模型数据计算得到(Marsland et al., 2003).各个GPS连续站相对应的大气负载,非潮汐海洋负载和水文负载形变通过双线性法对模型数据进行插值得到.为了和GPS垂向位移的日分辨率统一,分别将大气和非潮汐海洋负载形变的3 h时间分辨率统一为每日时间分辨率.图3为经过处理后KMIN连续站对应的水文负载、大气负载、非潮汐海洋负载形变.
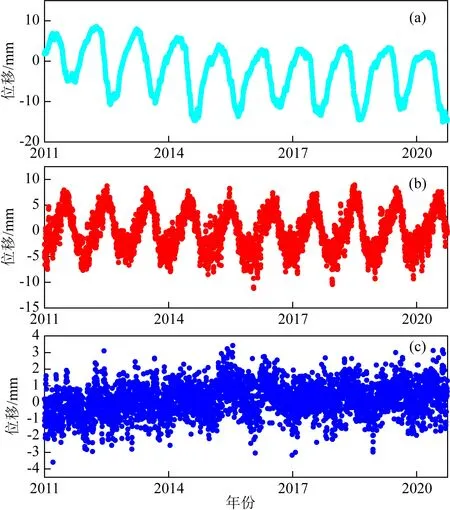
图3 KMIN连续站对应的水文(a)、大气(b) 、非潮汐海洋负载(c)形变Fig.3 hydrological (a), Atmospheric (b), non-tidal ocean (c) load deformation of KMIN station
1.3 奇异谱分析
提取GPS垂向位移中季节性信号的方法主要有小波分解法(Bogusz and Klos, 2016)、卡尔曼滤波法(Davis et al., 2012)、基于最小二乘拟合的谐波模型法(Blewitt and Lavallée, 2002)、SSA方法(Chen et al., 2013)等,但这些方法各具优缺点,如小波分解法中需要根据经验提前定义小波基函数和分解层数,不同的小波基函数和分解层数对季节性信号提取影响较大;卡尔曼滤波法的随机过程需要提前估计,程序运行耗时较长;基于最小二乘拟合的谐波模型法最为常用,然而,该方法提取出的周年、半周年项振幅和相位均为常数,不符合GPS垂向位移中实际的季节性变化.SSA方法是一种针对时间序列中信号分组与重构的方法,它的优势在于不需要任何外在的假设条件和先验信息,不仅能够提取时间序列数据中的非线性趋势信号,且不受正弦波假定的约束,能够稳定可靠的识别与强化周期信号等,因此,特别适合分析和提取有周期振荡的时间序列数据.
将时间跨度为2011年1月—2020年9月云南地区27个连续站的GPS垂向位移作为原始时间序列{y1,y2,y3,…,yn},设定窗口长度M(M (5) 1)计算滞后矩阵X的自协方差矩阵C及特征值λ1≥λ2≥…λM≥0和特征向量Ekj,如下式(6): (6) 2)计算滞后矩阵X在特征向量Ekj上的投影,即为时间主成分,如式(7)所示: (7) 3)时间序列的重建(Reconstruction Component, RC).由第k个时间主成分和特征向量按照式(8)进行重建(Vautard et al., 1992). (8) (9) 连续小波变换将小波基函数作为带通滤波器运用于分析具有时间序列的数据(Grinsted et al.,2004),可以很好地揭示单一时间序列数据的多时间-尺度变换特征的振荡周期.对于某个连续站的GPS垂向位移xn(n=1,2,…,N),将其连续小波变换定义为 (10) WXY=WXWY*, (11) 式(11)中,*表示复共轭,小波功率受边缘效应影响较大的区域为影响堆(Cone of Influence, COI).为了准确描述xn,yn的相位关系,选择COI区域之外一系列相位角的圆域平均值来衡量: (12) 交叉小波的相似性定义为 ρi=cos(am), (13) 式(13)中,ρ取值范围为-1到1,0代表不相关. 交叉小波变换能够很好地揭示GPS垂向位移和LSDM形变共同的高能量区及时频域中的相位关系.小波相干性则能够很好地弥补交叉小波变换在低能量区的不足,用来度量时频域中两者的局部相关密切程度,即对应交叉小波功率谱中低能量值区.连续站的GPS垂向位移和LSDM形变xn,yn的小波相干谱定义为 (14) 式(14)中,S是平滑窗口,s是小波尺度,Rn(s)是局部相干系数. 为了更好的对比分析GPS垂向位移与LSDM形变的季节性变化关系,从GPS垂向位移中去除由1.2节中介绍的方法得到的大气和非潮汐海洋负载形变,然后使用最小二乘法(Least Squares Fitting, LSF)对27个连续站的GPS垂向位移进行去线性趋势处理.27个连续站的GPS垂向位移和LSDM形变均出现季节性变化且整体运动趋势较为一致,大部分连续站的GPS垂向位移变化范围在-30 mm至30 mm,相对应的LSDM形变位移值范围在-10 mm至10 mm,说明水文负载形变并不能完全解释GPS垂向位移的季节性变化,水文负载形变是引起云南地区GPS垂向季节性变化的主要影响因素之一(Tesmer et al., 2011).图4为KMIN、XIAG、YNMH和YNTC连续站的GPS垂向位移和LSDN形变的比较.图4中YNMH、YNTC和XIAG连续站的相位和振幅具有较好的一致性,YNMH、YNTC和XIAG连续站位于云南地区陆地水变化较大的区域,说明在陆地水变化较大的区域,水文负载形变能够很好地解释GPS垂向位移的季节性变化.KMIN连续站在2011—2014年的相位吻合度较差,说明该时段水文负载形变不能很好地解释GPS垂向位移的季节性变化,可能受站点局部环境、系统误差及噪声影响较大.如果GPS垂向位移和LSDM形变的周期性具有一定的相关性,则有两种情况:1)GPS垂向位移和LSDM形变的周期项为同一周期,他们都是由同一个物理因素造成的,只是因他们的分辨率或者获取的方法不同,从而显现出两个周期;2)如果GPS垂向位移和LSDM形变周期项的物理因素之间具有相关性.那么,可以使用皮尔逊相关系数(如式(15))来判断GPS垂向位移与LSDM形变是否为同一周期项或者由同一物理因素产生的周期振动.27个连续站的GPS垂向位移与LSDM形变的相关系数计算结果如表1所示,两者的相关性平均为0.59,相关性最小的为YNGM连续站,值为0.15;相关性最大的为YNLJ连续站,值为0.76,说明大部分连续站的GPS垂向位移与LSDM形变具有较强的相关性.为了进一步说明GPS垂向位移与LSDM形变季节性变化的一致性,本文使用从GPS垂向位移中扣除LSDM形变后的RMS减少量(如式(16))来定量评估LSDM形变能否有效改正GPS垂向位移的非构造形变,若RMS减少量值为正值,说明LSDM形变能够有效的改正GPS垂向位移中的非构造形变,计算的RMS减少量结果如表1所示.从表1可知,除了YNGM连续站的RMS减少量值为负值之外,其他连续站的值都为正值,说明LSDM形变都能够有效去除这些连续站中的非构造形变;所有连续站的RMS减少量平均值为17.13%,说明GPS垂向位移中所包含的非构造形变,平均约17.13%来源于LSDM形变. 图4 KMIN (a)、XIAG (b)、YNMH (c)和YNTC (d)连续站的GPS垂向位移与相对应的LSDM形变Fig.4 GPS vertical displacement and corresponding LSDM deformation for KMIN (a),XIAG (b),YNMH (c) and YNTC (d) 表1 GPS与LSDM相关系数和RMS减少量Table 1 Correlation coefficient and RMS reduction between GPS and LSDM (15) (16) Wdowinsk 等(1997)研究表明,区域GPS网中不同连续站的GPS垂向位移中会存在时空相关的非构造形变噪声,称为共模误差,这类非构造形变噪声来源不明确,有可能来源于观测环境的好坏,地表质量负载和GPS数据解算的系统误差等.通常情况下在GPS垂向位移中去除速度项和周期项后的残差时间序列中进行共模误差提取,但是周期项信号中可能包含部分共模误差,因此,对去除速度项之后的GPS垂向位移残差时间序列进行共模误差提取.对云南地区的27个GPS连续站使用主成分分析计算出该地区的共模误差.图5为KMIN、XIAG、YNMH和YNTC连续站的GPS共模误差和LSDM形变的对比,从图5中可知,GPS共模误差和LSDM形变的整体运动趋势更为一致,使用式(15)定量计算两者的相关性,结果如表2所示,所有连续站的GPS共模误差与LSDM形变的平均相关系数为0.75.若从GPS共模误差中去除LSDM形变后,所有连续站的RMS减少量平均为35.72%,所以在云南地区的GPS共模误差与LSDM形变具有很好的相关性和一致性.因此,水文负载是该地区GPS共模误差的主要成份,这一结果与盛传贞等(2014)的结果一致. 图5 KMIN (a)、XIAG (b)、YNMH (c)和YNTC (d)连续站的GPS共模误差与LSDM形变对比Fig.5 Comparison of GPS common mode error and LSDM deformation for KMIN (a),XIAG (b),YNMH (c) and YNTC (d) 表2 GPS共模误差与LSDM形变的相关系数和RMS减少量Table 2 Correlation coefficient and RMS reduction between GPS common mode error and LSDM deformation 为了进一步分析GPS垂向位移与LSDM形变的关系,分别使用连续小波变换、交叉小波变换和小波相干性对两者进行周期分析,选取Morlet小波作为母函数.由于连续站数目较多,本文以YNTC连续站作为实例进行详细介绍.图7为YNTC连续站的GPS垂向位移与LSDM形变的连续小波、交叉小波和小波相干性的功率谱.图6a和6b的连续小波功率谱中黄色与蓝色分别表示能量密度的峰值和谷值,从蓝色到黄色,表示小波能量谱依次递增.黑色粗实线封闭区域表示通过了95%置信水平的显著性检验,黑色细实线下方为COI区域.从图6a中YNTC连续站的连续小波功率谱可知,GPS垂向位移在全时域范围内存在256~512天(0.7~1.4a)的主振荡周期且通过了显著性检验,在2013—2016和2018—2020时间范围内存在128~256天(0.4~0.7a)的主振荡周期且通过了显著性检验,图6a中小于128天的GPS垂向位移中高频部分没有显著的振荡周期.从图6b中LSDM形变的连续小波功率谱可知,LSDM形变在全时域范围内存在128~256天(0.4~0.7a),256~512天(0.7~1.4a)的主振荡周期且通过了显著性检验.由图6a和6b的结果表明,YNTC连续站的GPS垂向位移与LSDM形变在全时间域内均具有显著的近年周期(256~512天)变化.与此同时,使用连续小波变换对其他连续站进行周期分析,其他连续站都呈现出相似的结果. 连续小波变换只是反映了GPS垂向位移与LSDM形变自身的时间-尺度变换特征,为了进一步分析GPS垂向位移与LSDM形变的相互周期特性,使用交叉小波变换和小波相干性来反映GPS垂向位移与LSDM形变在高能量区和低能量区及其相位关系.如图6c所示,黑色箭头反映了参与交叉小波变换分析的GPS垂向位移与LSDM形变的相位关系: 若规定箭头方“→”表示二者相位相同,则“←”是相位相反;若箭头“↑”表示GPS提前LSDM 1/4 周期,则“↓”为LSDM提前GPS 1/4 周期. 从图6c中交叉小波功率谱可知,YNTC连续站的GPS垂向位移与LSDM形变在全时域内存在128~256天(0.4~0.7a),256~512天(0.7~1.4a)的共振周期,且通过了显著性检验.从图6d中小波相干功率谱低能量区,GPS垂向位移与LSDM形变存在部分时域内小于128天的共振周期,说明LSDM形变在高频部分不是造成GPS垂向位移主要的驱动力,可能是由GPS中系统误差引起的(Ray et al., 2008).其他连续站的GPS垂向位移与LSDM形变在全时域内均存在256~512天(0.7~1.4a)的共振周期,在部分时域内存在128~256天(0.4~0.7a)的共振周期.因此,本文主要关注GPS垂向位移和LSDM形变共同存在的256~512天的近年周期变化,从图6c可知,在256~512天的共振周期内的相位比较稳定,所以本文使用年周期的平均相位来表示GPS垂向位移与LSDM形变在256~512天的平均相位关系.表3为所有连续站在年周期变化的GPS垂向位移与LSDM形变的平均相位关系.除此之外,交叉小波的平均相位相似性更能反映GPS垂向位移与LSDM形变在不同时域上的相关性,所以计算GPS垂向位移与LSDM形变在年周期变化的平均相位相似性,结果如图7所示:YNWS、KMIN、YNMZ、YNHZ、YNML、YNTH、YNDC和YNJP连续站年周期变化的平均相位相似性大小低于0.9.这些平均相位相似性低于0.9的连续站位于云南地区东部小江断裂带附近,年降雨量较少.云南地区降雨量在时间上具有显著的年周期性特征,季节性降雨是导致该地区地壳垂向周期性变化的主要因素.云南地区的降雨量主要受孟加拉湾和南海的暖湿气流影响,形成了从南到北逐渐减少,东部小于西部的特点(赵宁坤等,2009; Zhan et al., 2017).因此,在降雨量较少,陆地水变化较小的云南东部地区的GPS连续站,水文负载引起的形变不能全部解释GPS年周期变化,其他因素(如其他地球物理因素、LSDM模型误差等)和水文负载形变共同作用引起了这几个连续站的年周期项变化,其他大部分连续站的年周期平均相位相似性大小在0.9~1之间,说明大部分连续站的GPS垂向位移与LSDM形变的年周期变化是物理相关的,水文负载形变是引起GPS年周期变化的主要原因. 图7 27个连续站的GPS垂向位移与LSDM的交叉小波平均相似性Fig.7 The mean semblance of cross wavelet between 27 GPS vertical displacement and corresponding LSDM deformation 表3 27个连续站的GPS垂向位移与LSDM形变的平均相位差Table 3 The average phase angle between 27 GPS vertical displacement and corresponding LSDM deformation 为了验证交叉小波变换方法的可靠性,图8展示了云南地区27个连续站通过XWT与LSF两种方法计算GPS垂向位移与LSDM形变年周期变化的相位差值结果:差异大部分在±6°以内;大部分连续站相吻合,这表明交叉小波变换可以在时频空间下有效检验GPS垂向位移与LSDM形变的相位关系. 图8 XWT与LSF两种方法获取27个GPS连续站与LSDM的年周期相位差对比Fig.8 The comparison of annual period phase difference between 27 GPS vertical displacement and corresponding LSDM deformation for XWT and LSF method 通过小波分析结果可知,不同连续站的GPS垂向位移与LSDM形变在不同时域内存在不同周期的季节性变化,因此,有必要使用一种高精度的季节性信号提取方法.在使用SSA方法对GPS垂向位移与LSDM形变进行季节性信号提取时,窗口大小和截取的主分量个数对于能否精确提取季节性信号显得尤为重要.多位学者使用SSA方法提取季节性信号时,通过多次实验得到窗口大小取两年最为合适(Chen et al., 2013; Li et al., 2017; Xiang et al., 2018),所以本文设定的窗口大小M=730,截取主分量个数则依据ω-correlation方法和统计重建后RC成分的方差贡献率大小来进行综合判断. 本文同样以YNTC连续站作为实例进行分析,使用ω-correlation方法分别对YNTC连续站的GPS垂向位移与LSDM形变的前20阶RC成分进行分析,从图9可知,GPS垂向位移从第5个RC成分之后,LSDM形变从第10个RC成分之后, RC成分之间的周期性分离较差,说明它们中噪声占主要部分.图9a中,GPS垂向位移中RC1-RC2、RC3-RC4的ω-correlation系数分别为0.98,0.99;图9b中,LSDM形变中RC1-RC2、RC3-RC4、RC6-RC7和RC8-RC9的ω-correlation系数分别为0.99、0.99、0.83、0.85,ω-correlation系数都大于0.6,可以看作是同一周期成分进行合并.同时分别统计前20阶RC成分的方差贡献率,从图10a可知,RC1和RC2的方差贡献率最大,分别为45%和32.4%;RC3和RC4分别为5.7%和4.8%,其他RC成分的贡献率较低,前4阶的方差贡献率总和为88%.从图10b可知,LSDM形变中RC1和RC2的方差贡献率最大,分别为51.4%和38%;RC3、RC4、RC5的贡献率分别为3.3%,3%,2.4%,其他RC成分方差贡献率较低,前9阶的方差贡献率总和为99%.综合方差贡献率和ω-correlation周期性分析,YNTC连续站的GPS垂向位移与LSDM形变的RC主分量截断数分别为4和9,所以利用SSA方法提取YNTC连续站的GPS季节性信号为RC1-RC4成分之和,LSDM季节性信号为RC1-RC9成分之和.为了对比SSA方法提取GPS垂向位移与LSDM形变的季节性信号效果,使用LSF方法分别对YNTC连续站的GPS垂向位移与LSDM形变进行季节性信号提取,提取结果如图11所示, SSA与LSF方法提取的季节性信号与原始数据整体运动趋势一致;相比于LSF方法,SSA方法提取的GPS季节性信号能够更加反映原始数据的季节性变化趋势.同理分别使用SSA和LSF方法对其他26个GPS连续站的GPS垂向位移与LSDM形变进行季节性信号提取.为了定量评估SSA和LSF方法提取季节性信号结果,分别计算SSA和LSF方法提取的季节性信号和GPS垂向位移和LSDM形变的相关系数和RMS减少量.计算结果如表4所示,SSA和LSF方法提取的季节性信号与GPS垂向位移的相关系数平均为0.73和0.64;RMS减少量平均为32.49%和24.05%;SSA和LSF方法提取的季节性信号与LSDM形变的相关系数平均为0.98和0.95,RMS减少量平均为82.77%和69.47%.通过对比可知,SSA方法提取的季节性信号要整体优于LSF方法. 图9 YNTC连续站的前20阶GPS(a)与LSDM(b)时间序列的w-correlation分析结果Fig.9 w-correlation analysis results of the first 20 order between GPS vertical displacement (a) and corresponding LSDM deformation (b) for YNTC station 图10 YNTC连续站的GPS(a)与LSDM(b)时间序列的前20阶的RC方差贡献率统计Fig.10 The first 20 order RC variance contribution rate statistics between GPS vertical displacement (a) and corresponding LSDM deformation (b) for YNTC station 图11 SSA与LSF方法提取YNTC连续站的GPS(a)与LSDM(b)的季节性信号Fig.11 Seasonal signals of GPS vertical displacement (a) and corresponding LSDM deformation (b) extracted by SSA and LSF for YNTC station 表4 SSA与LSF方法提取的GPS与LSDM季节性信号的相关系数和RMS减少量Table 4 Correlation coefficient and RMS reduction between GPS and LSDM seasonal signals extracted by SSA and LSF methods 通过表1可知,除YNGM连续站的RMS减少量为负值之外,其他连续站的RMS减少量均为正值.因此,为了获得高精度的云南地区27个GPS垂向速度场,除了YNGM连续站之外,其他GPS连续站都使用水文负载模型数据进行改正处理,然后对所有连续站再使用主成分分析方法(Dong et al., 2006)进行共模误差剔除,国内外学者普遍认为白噪声和闪烁噪声组合的噪声模型能够代表大部分GPS垂向位移的噪声特性(Williams et al., 2004;Didova et al., 2016;He et al., 2019),因此,在经过水文负载模型和共模误差预处理后,最后使用Hector软件(Bos et al., 2013)通过白噪声和闪烁噪声组合模型估计所有连续站的速率及不确定度.图12为最后得到的2011—2020年云南地区的垂向速度场,从图12中可知,云南地区以红河断裂带为界划分滇西南块体,以红河断裂带、小江断裂带和丽江-小金河断裂组成川滇块体南部.滇西南块体中除YNMJ连续站以0.89 mm·a-1速率抬升之外,其他连续站以0.01~1.9 mm·a-1的速率沉降;而川滇块体南部除YNYS和YNYM连续站速率分别以0.1 mm·a-1和0.05 mm·a-1沉降之外,其他连续站以0.13~2 mm·a-1速率抬升. 图12 云南地区2011—2020年的GPS垂向速度场(红色和蓝色箭头分别代表抬升和沉降速率)Fig.12 GPS vertical velocity field in Yunnan region during 2011—2020(Red and blue respectively represent the up and down vertical rates) 川滇块体南部的整体抬升与小江断裂的左旋剪切运动密切相关,由空间大地测量的研究结果表明小江断裂带的运动速率为7~13 mm·a-1(Shen et al., 2005; Zheng et al.,2017; 李长军等, 2019),导致川滇块体整体南向运动,并受阻于南部的红河断裂带,使得川滇块体南部发生抬升.而滇西南块体沿着高黎贡右旋走滑断裂和南汀河左旋断裂与勐兴左旋断裂大规模旋转运动(Tong et al., 2021),在滇西南块体的中东部形成拉张而沉降. Hao等(2016)使用GRACE模型数据去除GPS垂向位移中非构造形变之后得到的云南地区2010—2015年GPS垂向速度场整体以0.1~3.4 mm·a-1的速率抬升为主(图13a).但是,本文得到的2011—2020年GPS垂向速度场结果与之(Hao 等(2016))相差较大,却与Zhan 等(2017)同样使用GRACE模型数据改正非构造形变之后得到的2010—2015年速度场(图13b)在运动趋势上大体一致,都是以红河断裂带为边界,滇西南块体以沉降为主,川滇块体南部以抬升为主,然而在具体数值上仍存在差异.本文得到的2011—2020年GPS垂向速度场与前人(Hao 等(2016)和Zhan等(2017))的结果有差异,原因可能如下:1)使用的GPS观测数据时间跨度不同,本文数据源是2011—2020年GPS连续站观测数据,Zhan 等(2017)和Hao 等(2016)所使用的数据源是2010—2015年GPS连续站观测数据,不同时间跨度内的构造形变信息存在不一致性,时间跨度越长对获取可靠准确的速度场更有益;2)使用的水文负载模型数据不同.本文所使用的是LSDM模型数据,Zhan 等(2017)和Hao 等(2016)所使用的是GRACE模型数据,地球物理数据源不同会导致垂直位移数值不相同,改正效果也会存在差异;3)本文对GPS垂向位移进行共模误差去除和噪声模型估计,虽然Hao等(2016)也做了共模误差和噪声模型估计处理,但是噪声模型和空间滤波方法不一样;而Zhan等(2017)并未做共模误差和噪声模型估计,因此导致部分连续站速度场数值存在差异. 图13 云南地区2010—2015年的GPS垂向速度场(a) 根据Hao等, 2016中速度场数据绘制; (b) Zhan等,2017文献中速度场图.Fig.13 GPS vertical velocity field in Yunnan region during 2010—2015(a) The velocity field is plotted according to the data from (Hao et al., 2016); (b) The velocity field diagram from (Zhan et al., 2017). 从表1中可知,YNGM连续站的GPS垂向位移与LSDM形变的相关性最低,且RMS减少量为负值,说明水文负载形变不是引起YNGM连续站GPS垂向位移中季节性变化的原因.本文分别从YNGM连续站的观测环境和建设质量情况以及周围气象站的降雨量和温度等多方面进行综合分析,判断造成YNGM连续站异常的原因.从陆态网络收集的资料可知建设的YNGM连续站为基岩墩标,且连续站附近没有大型湖泊、河流.通过对收集到2011年1月—2020年4月时间段YNGM连续站观测的MP1和MP2多路径效应值及数据观测有效率来判断周围环境的观测质量,如图14所示,MP1和MP2值大部分在0.5 m以下,且数据有效率大部分在90%以上,由此可知YNGM连续站观测环境质量不是造成异常的原因.为了进一步分析YNGM连续站是否受降雨量与温度的影响,本文收集到了YNGM连续站距离最近约为29 km气象站在2011年1月—2020年6月间观测的温度与降雨量数据,收集的月降雨量和温度如图15所示,降雨量与温度变化均存在着季节性变化,月平均温度,月平均最高温度和月平均最低温度范围分别在11.6°~25.7°、20.1°~33.2°、5.2°~21.6°,因此可以排除基岩的热胀冷缩,冰川覆盖、冰雪消融等情况造成YNGM异常的原因.YNGM连续站附近气象站观测的月累积降雨量比较大,由于LSDM模型数据得到的水文负载形变不包含地下水变化引起的形变.综合因素考虑,地下水变化、LSDM模型和GPS解算的系统误差可能是造成YNGM连续站中GPS垂向位移与LSDM形变相关性和一致性较差的主要原因. 图14 YNGM连续站的数据观测有效率和多路径效应误差,数据来源:中国地震局GNSS数据产品服务平台(ftp:∥ftp.cgps.ac.cn)Fig.14 Data quality inspection results of YNGM station from 2011 to 2020, Data source: GNSS data product service platform of China Earthquake Administration (ftp:∥ftp.cgps.ac.cn) 图15 YNGM连续站在2011年1月—2020年6月的月降水量和最高最低平均温度,数据来源:中国气象数据网(http:∥data.cma.cn)Fig.15 Monthly precipitation and max, mean, min temperature changes at YNGM station from January 2011—June 2020. Data source: China Meteorological Data Network (http:∥data.cma.cn) 本文使用时间跨度在2011—2020年的27个连续站的GPS垂向位移和LSDM形变来研究云南地区的垂向运动的季节性变化,对比分析了GPS垂向位移及GPS共模误差与LSDM形变的定量关系和变化特征,并使用了SSA方法提取GPS垂向位移和LSDM形变的季节性信号和使用连续小波变换、交叉小波变换和小波相干性分析GPS垂向位移和LSDM形变的周期关系,最后得到了云南地区2011—2020年的GPS垂向速度场,本文得出的主要结论如下: (1)GPS垂向位移和LSDM形变的整体运动趋势一致,但是,LSDM形变的位移值范围要整体小于GPS的,说明LSDM形变能解释部分GPS垂向运动季节性变化.GPS共模误差与LSDM形变的平均相关系数为0.75,若从GPS共模误差中去除LSDM形变后, RMS减少量平均为35.72%,说明GPS共模误差物理成因中大约有35.72%来源于LSDM形变. (2)通过小波分析结果可知,大部分GPS连续站的周年平均相位相似性大小为0.9~1,说明LSDM形变与GPS垂向位移在年周期项变化是物理相关的,进一步说明水文负载形变是GPS年周期变化的主要驱动力,少部分GPS连续站是由其他因素和水文负载形变共同作用造成了GPS年周期项变化.相比于LSF方法提取的GPS垂向位移和LSDM季节性信号,SSA方法提取的季节性信号更加符合GPS垂向位移与LSDM实际的季节性运动. (3)2011—2020年云南地区垂向速度场显示滇西南块体主要以0.01~1.9 mm·a-1的速率沉降,滇中块体主要以0.13~2 mm·a-1速率抬升. 致谢“中国大陆构造环境监测网络”提供的GNSS数据产品,德国波斯坦地学中心提供的地表质量负载数据,在此一并表示感谢!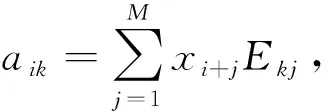

1.4 小波分析
2 结果
2.1 GPS垂向位移与水文负载形变比较


2.2 GPS共模误差与水文负载形变比较


2.3 小波谱分析



2.4 季节性信号提取




2.5 云南地区垂向地壳形变

3 讨论
3.1 云南地区垂向速度场差异分析

3.2 异常的YNGM连续站分析


4 结论
