基于地面重力的卫星重力梯度检校方法
2021-08-03瞿庆亮常晓涛朱广彬于胜文周苗刘伟
瞿庆亮, 常晓涛* , 朱广彬, 于胜文, 周苗, 刘伟
1 山东科技大学测绘科学与工程学院, 山东青岛 266590 2 自然资源部国土卫星遥感应用中心, 北京 100048
0 引言
地球重力场卫星可以高效探测地球重力场的精细结构,尤其是2009年欧洲航天局发射的GOCE(gravity field and steady-state ocean circulation explorer)卫星,作为全球首颗以重力梯度观测模式恢复高精度高分辨率地球重力场的地球重力卫星,能够以100 km空间分辨率构建1~2 cm精度的全球大地水准面模型和1 mGal精度的地球重力场模型(Bouman et al., 2011, 2016; Bouman and Fuchs, 2012; Van Der Meijde et al., 2015; Xu et al., 2017; Siemes, 2018),为人类更深入地了解地球的内部结构和研究海洋环流提供了丰富的地球观测基础数据.GOCE卫星的核心载荷是星载静电重力梯度仪,其具有高灵敏特性,可以高精度探测地球重力场的中短波信号,配合SST-hl(Satellite-to-Satellite Tracking in the high-low mode)技术获取的地球重力场的长波信号,可实现高精度地球重力场的恢复(蔡林等, 2012; 朱广彬等, 2018; Liang et al., 2020; 刘焕玲等, 2020).但梯度仪受卫星空间环境及观测条件影响,观测值中存在难以避免的噪声,这会增加重力场恢复数据处理的难度,并进一步对重力场恢复的精度和分辨率产生不利影响.在轨检校是顾及梯度仪存在观测噪声的实际情况,通过对其在轨标定最大限度地消除观测系统误差,提高重力场恢复的精度和分辨率.因此,在卫星总体任务确定的情况下,有效的在轨检校显然能降低卫星工程系统对梯度仪研制的指标要求,对控制卫星工程成本、提高观测质量、实现工程总体要求具有重要意义.
研制梯度模式地球重力场探测卫星是我国《国家民用空间基础设施中长期发展规划(2015—2025年)》的重要内容.突破卫星在轨检校相关技术,面向我国发展梯度模式重力卫星的总体任务,研究提出针对性的卫星梯度仪在轨检校方法是顺利完成规划任务、确保工程技术达到国际先进水平的关键.在此相关研究领域,国际上,Arabelos和Tscherning(1998)提出利用地面重力对卫星重力梯度观测值进行检校的方法之后,Wolf和Denker(2005)利用地面重力验证了卫星轨道高度处的卫星重力梯度张量观测值,并将各分量上重力梯度延拓值与观测值进行了差异比对.此外,Eshagh(2010, 2011)研究提出利用地面重力以及大地水准面高计算卫星重力梯度的方法,并在此基础上对卫星重力梯度张量观测值进行检校和验证.prlák等(2015)在Eshagh研究的基础上,提出利用卫星测高数据计算卫星重力梯度的方法.Yildiz等(2016)在南极地区利用航空重力数据,对GOCE重力梯度张量实测数据进行了验证.Bouman和Fuchs(2012)利用先验重力场模型对测量带宽内的重力梯度值进行了验证.Rispens和Bouman(2011)联合先验重力场模型与星敏感器数据对加速度计测量值进行了检校.国内学者针对GOCE卫星的在轨检校工作进行了跟踪研究.罗志才等(2009)在开展GOCE卫星重力梯度测量数据预处理方法研究的基础上,讨论了利用重力场模型、GOCE SST数据以及地面重力数据对GOCE卫星在轨检校的技术方法.吴云龙(2010)利用地面重力对GOCE卫星的在轨检校方法进行了进一步的研究.徐新禹等(2015)对同阶次的不同重力场模型、同一模型不同阶次以及是否考虑漂移参数对GOCE重力梯度观测值检校的影响进行了系统分析.这些基于GOCE卫星的在轨检校技术方法为我国自主梯度模式重力卫星的检校提供了良好的技术基础.
总的来说,国内外学者对利用地面实测重力或地球重力场模型实现梯度仪在轨检校进行了比较广泛和深入的研究,为GOCE卫星的在轨检校做出了重要贡献,但在地面重力数据的空间尺度、精度以及梯度仪本身噪声对在轨检校影响方面的综合分析研究存在明显不足,在提高检校效果、降低研制成本方面尚存在一定的发展空间.本文吸收国际国内对卫星梯度仪在轨检校的最新技术成果,在借鉴GOCE卫星在轨检校方法的基础上,面向中国发展的梯度模式重力卫星的规划任务,研究提出一种综合考虑地面重力数据空间尺度、精度并顾及梯度仪噪声的卫星重力梯度在轨检校方法,通过球谐分析与球谐综合将地面数据延拓至卫星轨道高度,利用旋转矩阵建立局部指北坐标系与卫星梯度仪坐标系的转换关系,成功实现地面数据与卫星观测数据的比对检校.
1 研究方法
1.1 地面重力向上延拓
地球质体外部引力位场是一个调和场,任意一点的引力位V满足Laplace方程.利用分离变量法,推导球近似条件下引力位的球谐级数展开式为:
(1)
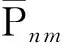
正常引力位V′的球谐级数展开式为:
(2)

T=W-U=V-V′.
(3)
将式(1)、式(2)代入式(3),得到扰动位T的球谐级数展开形式如下:
(4)

由地面重力异常Δg与扰动位的关系:
(5)
推导得到地面重力异常的球谐函数展开表达式为:
(6)
根据球谐函数的正交性,由地面重力异常计算扰动位系数公式如下:
(7)
扰动位系数加上正常位系数得到引力位系数后,利用球谐综合将地面重力向上延拓得到卫星高度处的重力梯度张量.局部指北坐标系(local north-oriented frame, LNOF)下,重力梯度张量Vzz分量可表示为如下形式:
重力梯度张量其他分量的表达形式可参见Petrovskaya和Vershkov(2006),由此即可实现与卫星梯度张量观测值的比对,并基于此开展卫星梯度仪的在轨检校.
1.2 检校模型构建
卫星重力梯度观测值是在梯度仪坐标系(gradiometer reference frame, GRF)下给出,而基于地面重力的梯度延拓值是在LNOF下,因此需要建立LNOF与GRF之间的转换关系,可由旋转矩阵表示为:
VGRF=RVGRFRT,
(9)
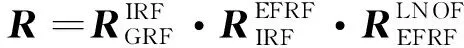

图1 GOCE卫星参考系统:OG-XGYGZG表示梯度仪坐标系,OS-XNYNZN表示局部指北坐标系,O-XIYIZI表示惯性坐标系,O-XEYEZE表示地固坐标系Fig.1 The reference systems for GOCE satellite. OG-XGYGZG is the GRF coordinate system, OS-XNYNZN is the LNOF coordinate system, O-XIYIZI is the IRF coordinate system, O-XEYEZE is the EFRF coordinate system
重力梯度观测值的在轨检校是利用外部独立数据计算的重力梯度值与卫星重力梯度观测值进行比较,建立函数关系式,进而求得检校参数,即:

(10)
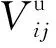
v=Ax-l,
(11)

利用最小二乘估计尺度因子和偏差参数,可得:
x=(ATPA)-1ATPl.
(12)
2 实验分析
根据卫星设计指标,对地面观测数据精度、空间尺度以及重力梯度仪观测噪声等关键检校要素开展实验分析.沿轨重力梯度张量采用EGM2008重力场模型,结合GOCE卫星精密轨道数据SST_PSO_2(precise science orbits)进行计算,数据时间从2011年2月11日至6月23日,采样率为1 s.
2.1 地面重力向上延拓与检校评估
为评估地面重力向上延拓精度,采用EGM2008重力场模型计算格网分辨率为0.25°×0.25°的全球重力异常,分别加入标准差为5 μGal、1 mGal和2 mGal的白噪声,作为地面重力起算数据,将其向上延拓得到卫星轨道处的重力梯度张量,与沿轨直接球谐综合计算的EGM2008重力梯度张量进行比较,得到重力梯度各分量的延拓误差,如表1所示.

表1 重力梯度张量各分量的延拓误差(mE)Table 1 Standard deviations of upward continuation errors of each component of gravitational gradients (mE)
从表1可以看出,基于地面重力数据得到的重力梯度张量各分量的向上延拓误差随着地面观测数据精度的降低而变大.当地面重力数据精度为5 μGal时,各分量延拓误差均在10-2mE水平;当地面重力数据精度为1 mGal时,各分量延拓误差在0.3~0.6 mE;当地面重力数据精度达到2 mGal时,各分量延拓误差在0.4~1.2 mE.参考GOCE卫星重力梯度张量四个高精度分量中,Vxx、Vyy分量在轨实际测量精度为10 mE/Hz1/2,Vzz、Vxz分量测量精度在20 mE/Hz1/2左右(Floberghagen et al., 2011; Rummel et al., 2011),基于地面重力的重力梯度向上延拓误差远小于GOCE卫星重力梯度观测值的噪声水平.图2给出了地面重力精度分别为5 μGal、1 mGal和2 mGal时,重力梯度张量对角线分量的向上延拓误差分布情况.
由图2可以看出,重力梯度张量对角线分量的向上延拓误差随机分布在卫星轨道上,即地面重力观测数据的地理分布对向上延拓误差产生的影响较小.当地面重力观测精度为5 μGal时,Vxx、Vyy两个分量的向上延拓误差较为接近,均在±0.2 mE以内,而Vzz分量则达到±0.4 mE;当地面重力观测精度为1 mGal时,Vxx、Vyy两个分量延拓误差范围达到±3 mE,Vzz分量增至±5 mE,相比5 μGal精度的地面重力,增幅较为明显;当地面重力观测精度在2 mGal时,Vxx、Vyy两个分量延拓误差范围为±4 mE,Vzz分量为±7 mE.由此看出,Vzz分量向上延拓误差大小约为Vxx、Vyy两个分量之和,但符号相反.

图2 重力梯度张量对角线分量的向上延拓误差分布Fig.2 The distribution of upward continuation errors in diagonal components of gravitational gradients
利用地面重力检校卫星重力梯度观测值,往往在0.005~0.1 Hz的测量带宽内进行(Veicherts et al., 2011).由于滤波后的重力梯度观测值中偏差参数很小,可以忽略不计,待检校参数一般只考虑尺度因子.因此,本文在重力梯度观测中加入尺度因子为1.05的待检校参数,并采用巴特沃斯带通滤波器对地面重力延拓值与沿轨重力梯度球谐综合值进行同样的滤波处理.以一周为检校周期(Bouman et al., 2011),求定的尺度因子结果如表2所示.

表2 重力梯度观测值尺度因子检校中误差Table 2 The root mean square errors of the scale factors of gravitational gradient observations
从表2可以看出,重力梯度观测值检校参数的确定精度与地面重力观测精度相关.其中,当地面重力观测精度在5 μGal水平时,检校得到重力梯度张量尺度因子的中误差在10-5~10-6量级;地面重力观测精度达到1 mGal时,尺度因子的中误差在10-4~10-6量级;地面重力观测精度为2 mGal时,尺度因子的中误差在10-4量级.检校后的重力梯度观测值应满足Laplace方程,重力梯度张量矩阵对角线分量之和,即重力梯度张量的迹理论值为零.当重力梯度观测值中存在误差,重力梯度张量的迹实际值通常不为零,此时迹越小,检校精度越高,以此对重力梯度观测值检校精度进行评价.利用不同精度的地面重力数据检校后,重力梯度张量的迹如图3所示.
由图3可以看出,利用5 μGal精度的地面重力对重力梯度观测值进行检校后,重力梯度张量的迹优于10-3mE;地面重力精度为1 mGal时,检校后的重力梯度张量的迹仍优于10-2mE;地面观测精度降至2 mGal水平时,检校后的重力梯度张量的迹偏大,在10-2~10-1mE量级.这说明,随着地面重力观测数据精度水平的提升,重力梯度观测值的检校精度会相应升高1个数量级左右. 目前地面重力数据获取精度在5 μGal,而航空重力数据获取精度也能达到1 mGal左右(Forsberg and Olesen, 2010),因此卫星重力梯度观测值在轨检校时,可采用地面重力或航空重力,其数据精度能够满足卫星重力梯度仪检校要求.

图3 地面重力数据检校后重力梯度张量的迹Fig.3 The gravitational gradient trace calibrated by ground gravity data
2.2 重力梯度仪噪声影响
卫星重力梯度观测值在测量带宽内呈现白噪声特性,不同噪声量级会对重力梯度仪检校产生较大影响.参考GOCE卫星重力梯度仪发射前的测量精度指标为6~7 mE,实际在轨测量精度在10~20 mE水平(Marque et al., 2010),本文在设计仿真实验时,在沿轨重力梯度球谐综合值中加入1.05的尺度因子,对其进行带通滤波处理后,加入标准差分别为6 mE、10 mE以及20 mE的白噪声,作为待检校的梯度观测值.利用5 μGal和1 mGal精度的地面重力对梯度观测值进行检校,得到的尺度因子中误差结果如表3所示.

表3 不同噪声水平的重力梯度观测值尺度因子检校中误差Table 3 The root mean square errors of the scale factors of gravitational gradient observations with different noise
从表3可看出,测量带宽内的重力梯度观测值在不同噪声量级影响下,利用5 μGal或者1 mGal精度的地面重力,计算得到六个分量上尺度因子的中误差均在10-4~10-6水平.这表明,利用高精度的地面重力能够高精度的求定不同观测噪声水平的重力梯度观测值中的检校参数.以重力梯度张量的迹作为检校精度评价指标,利用5 μGal精度的地面重力对不同噪声水平下的梯度仪观测值进行检校后,重力梯度张量的迹如图4所示.
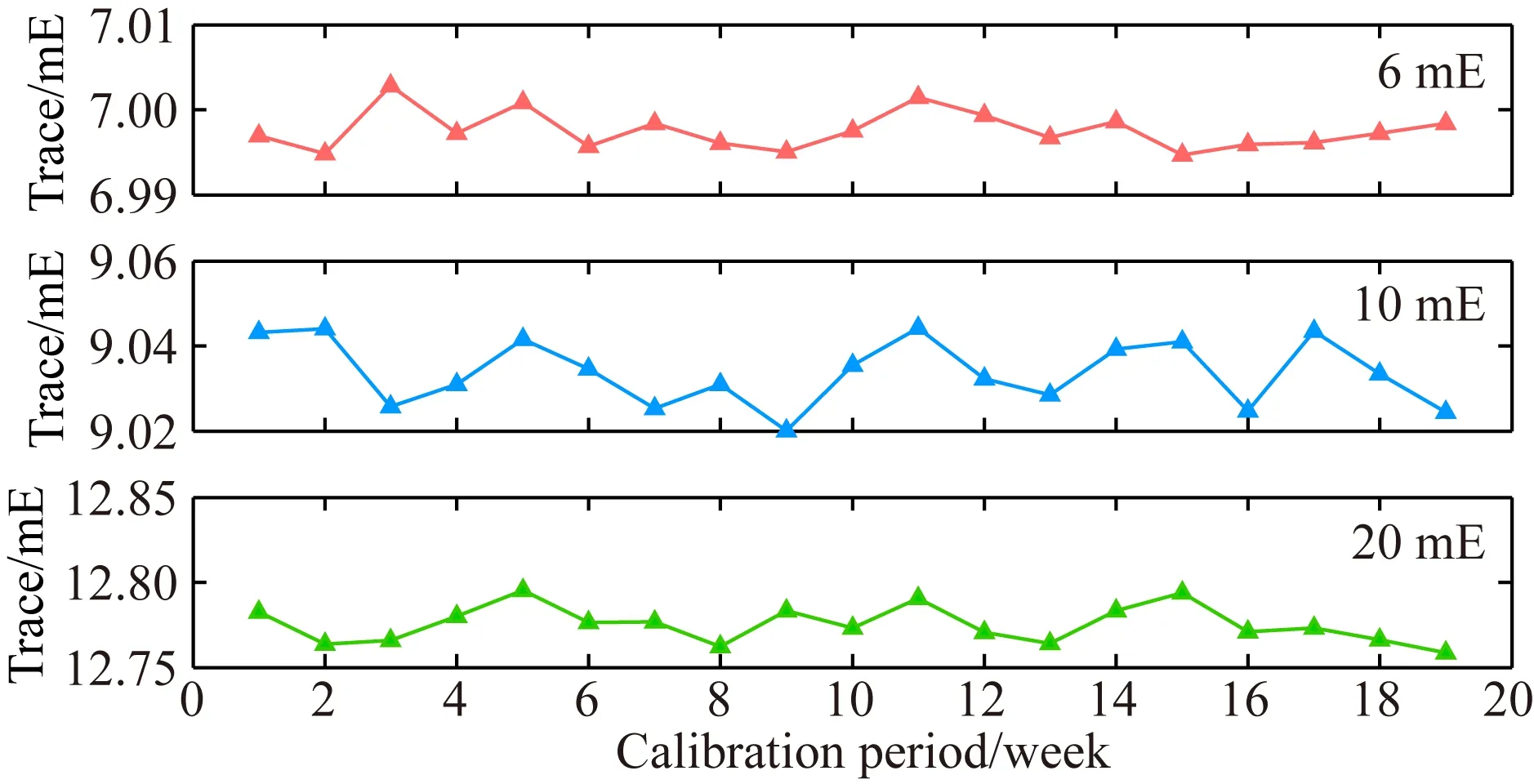
图4 不同噪声水平的梯度仪观测值检校后重力梯度张量的迹Fig.4 The calibrated gravitational gradient trace with different noise of gradiometer observations
由图4可以看出,检校后重力梯度张量的迹随着梯度仪观测值噪声增加而变大,不同噪声水平下,检校后重力梯度张量的迹分别为7.0 mE、9.0 mE和12.8 mE左右.结合表3和图4可以得到,基于地面重力的重力梯度观测值在轨检校可以有效消弱观测值中的系统偏差,但观测值中的偶然误差仍会对检校后重力梯度张量的迹产生较大的影响.GOCE卫星发射前,重力梯度张量的迹精度指标要求为11 mE(Siemes et al., 2012; Stummer et al., 2012),考虑到未来国产重力梯度仪的精度要优于该指标,因此其测量噪声控制在10 mE以内较为合适.
2.3 地面重力空间尺度影响
利用地面重力对卫星重力梯度观测值进行在轨检校时,由于观测成本限制,地面重力实地观测空间尺度是有限的,可采用中心区域实测地面重力数据、外部区域先验重力场模型值填充的方式进行.
考虑到EGM2008重力异常精度约为10 mGal(章传银等, 2009; Pavlis et al., 2012),本文研究中,在外部区域的EGM2008模型重力异常中加入标准差为10 mGal白噪声作为填充值,在中心区域的EGM2008模型重力异常中分别加入标准差为5 μGal和1 mGal的白噪声,作为实测地面重力,进行向上延拓后,将延拓的重力梯度值与沿轨直接球谐综合计算的EGM2008重力梯度值进行比较.不同空间尺度下,重力梯度各分量向上延拓误差如图5所示.
由图5可以看出,检校中心区域采用5 μGal或者1 mGal精度的地面重力向上延拓时,重力梯度各分量的延拓误差随地面重力空间尺度的增加有逐渐变小的趋势.相同空间尺度下,检校中心区域采用5 μGal精度的地面重力向上延拓得到的重力梯度张量延拓误差要小于1 mGal精度的地面重力;对于重力梯度分量而言,Vzz、Vxz及Vyz三个分量延拓误差相较其他几个分量略大.由于GOCE重力卫星测量带宽下限为0.005 Hz,相当于卫星飞行200 s,因此在利用地面重力检校梯度观测值时,要求检校中心区域至少为12°×12°.在该尺度条件下,中心区域采用5 μGal精度的地面重力,重力梯度六个分量的延拓误差在0.2~0.4 mE;中心区域采用1 m Gal精度的地面重力,重力梯度六个分量的延拓误差在0.2~0.9 mE.
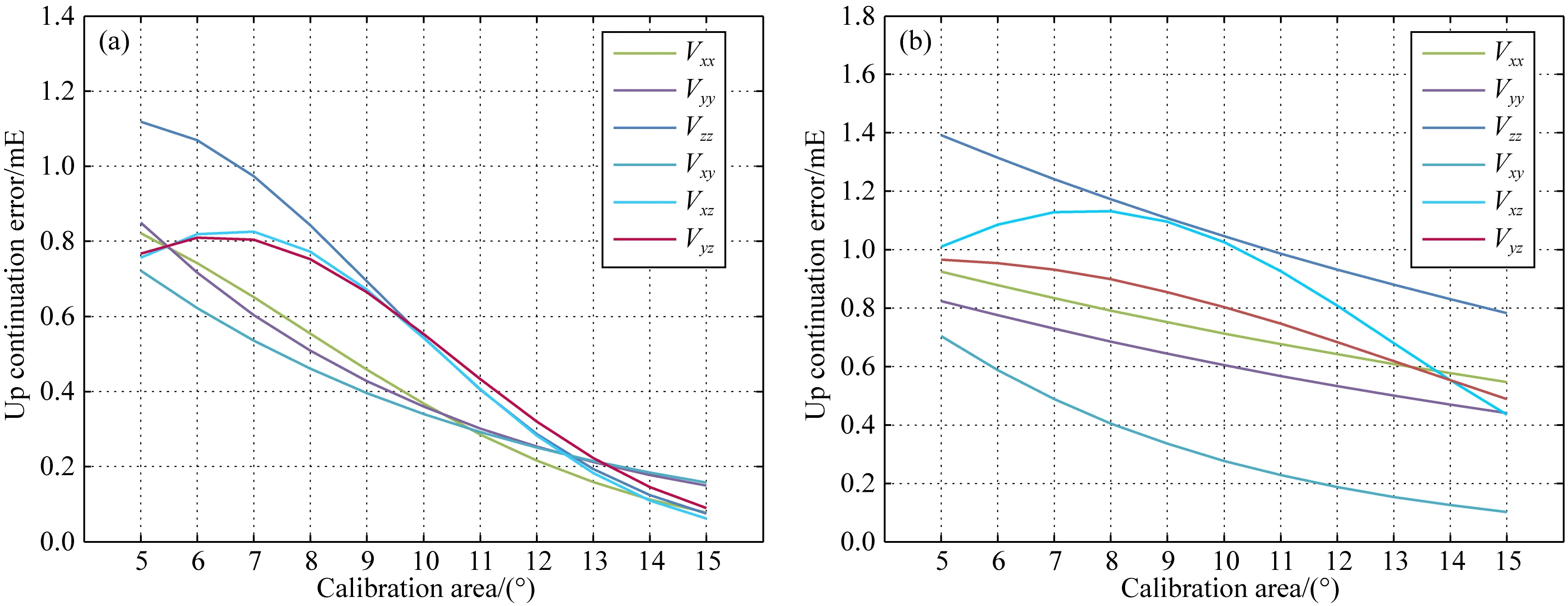
图5 不同空间尺度下地面重力向上延拓误差(a) 5 μGal地面重力; (b) 1 mGal地面重力.Fig.5 The upward continuation errors for different calibration areas with the precision of ground gravity data in 5 μGal (a) and 1 mGal (b)
同样,利用局部地面重力对重力梯度观测值进行在轨检校需在测量带宽内进行,研究中将沿轨重力梯度球谐综合值作为真值,加入1.05的尺度因子后对其进行带通滤波,并加入标准差为10 mE的白噪声,作为待检校的梯度观测值.当地面重力观测精度为5 μGal,空间尺度为12°×12°时,利用地面重力检校得到卫星重力梯度观测值六个分量上尺度因子的统计结果见表4.
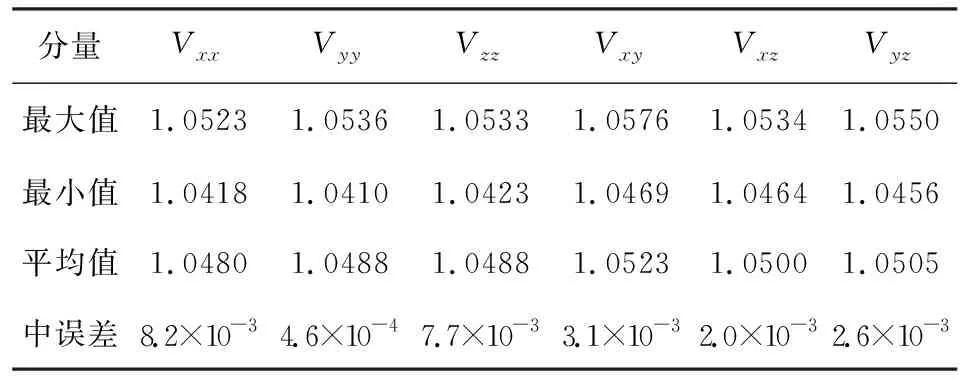
表4 地面观测空间尺度为12°×12°时检校得到的尺度因子统计值Table 4 The statistical values of the scale factors when the ground gravity data in a calibration area of 12°×12°
从表4可以看出,检校得到的重力梯度观测值尺度因子的平均值与1.05之间最大差异为0.002,尺度因子中误差在10-3~10-4量级.这说明,利用12°×12°的地面重力观测数据,能够以较高精度确定出检校参数.此外,将检校前后重力梯度张量的迹与梯度仪观测值只含有白噪声时的重力梯度张量的迹进行了对比,并计算了检校前后重力梯度Vzz分量的变化,如图6所示.

图6 重力梯度张量的迹(a)以及Vzz分量(b)检校前后的变化Fig.6 The differences before and after calibration of gravitational gradient trace (a) and Vzz component (b) of gravitational gradients
由图6可看出,检校前重力梯度张量的迹平均值在9.5 mE水平,在利用地面重力数据对梯度观测值进行检校后,重力梯度张量的迹平均值约为9.0 mE水平,与梯度观测值只含有白噪声条件下的梯度张量的迹水平一致,这说明重力梯度观测值中白噪声的存在是导致检校后重力梯度张量的迹不为零的主要因素;对于重力梯度Vzz分量而言,在检校前观测值与真值之间差异较为明显,其值在19.3 mE,这是由于梯度观测值中的尺度因子和噪声共同影响的结果,而检校后观测值与真值的差异在4.4 mE,相比检校前有了明显提升.这表明利用本文设计提出的基于地面重力的卫星重力梯度在轨检校方法可有效实现未来我国自主重力卫星梯度仪的高精度在轨检校.
3 结论
作为重力梯度卫星任务的重要技术环节,重力梯度仪的在轨检校和观测值的在轨验证可有效改善重力梯度卫星数据预处理效果,提高卫星观测质量.本文面向我国未来重力梯度卫星发展规划,研究了基于地面重力的卫星重力梯度观测值的在轨检校方法,从地面观测数据精度、空间尺度以及重力梯度仪观测噪声等检校要素进行了分析研究以及实验验证.结果表明,在12°×12°的地面检校区域内,利用精度优于1 mGal的地面重力观测数据即可实现观测噪声低于10 mE的重力梯度仪高精度在轨检校.在此条件下,重力梯度张量各分量延拓误差相比梯度仪观测噪声低一个量级,并且能够以10-3~10-4水平确定检校参数,检校后重力梯度张量的迹在8.7~9.4 mE水平,可有效实现我国国产卫星重力梯度仪的高精度在轨检校.
致谢感谢ESA(European Space Agency)提供的GOCE卫星数据和ICGEM(International Centre for Global Earth Models)提供的EGM2008全球重力场模型.
