基于演化博弈的民航旅客群体性事件处置策略

2021-08-03袁佳，邵荃

科学技术与工程 2021年19期

袁佳，邵荃

(南京航空航天大学民航学院，南京 211106)

随着民航业迅猛发展，各家航空公司纷纷增加航线以满足日益增长的旅客需求，因此航班延误问题也愈发突出，在此背景下，旅客极其容易产生不满情绪，继而引起旅客群体性事件的发生，这无论是对旅客、机场、航空公司，还是其他各方都将会产生相当恶劣之影响。

文献[1]在分析航班延误定义及原因的基础之上，研究旅客群体性事件处置中存在的问题，从而对此提出合理且有效的应对策略。文献[2]构建了基于最大偏差原则的多属性评价模型，以此来研究分析群体性突发事件的矛盾对抗性特征，最后再结合真实案例，从而分析全样本的调查数据。文献[3]对社会燃烧的相关研究与成果进行分析及总结，然后在此基础之上，再对延误所导致的各种相关突发情况的现状及原因进行分析，并提出相应的处置对策及原则。文献[4]以广州白云国际机场相关突发状况作为研究分析对象，然后对民航业内所发生的群体性事件，其主要特点、原因，以及于目前举措方面有所制约的相关因素进行总结，并从事前、事中及事后三个方面分别提出应对的具体措施。此外，文献[5]将演化博弈理论、系统论、突变理论及社会网络分析等基础知识全部结合在一起，然后在此基础之上，再分析大面积延误背景中，为何会发生群体性事件，其自身是否存在着相关的诱发因素，并最终构建了非线性的预警机制。而文献[6]基于动力学模型、前景理论和动态博弈方法，研究不同延误处置策略对旅客满意度及航空公司经济效益的影响作用。文献[7-9]则是从旅客角度出发，研究了不同情景中旅客间的相互影响及情绪变化。

目前对于群体性事件处置的研究主要集中于分析群体性事件的原因、特点及处置中存在的问题，并基于此提出相关的策略和措施，却忽略了在大面积航班延误情景中，由于同一候机区域有着多个航班的旅客，旅客的情绪与满意度变化不仅取决于所乘航空公司采取的处置措施，而且会不可避免地受到其他航空公司实施策略的影响。因此必须平衡不同航班旅客群体的服务需求和满意度，协调多家航空公司处置方案，构建更加行之有效的对群体性事件处置策略模型。

现结合演化博弈的相关理论，对各航空公司之间的演化博弈过程进行分析，从而建立航空公司处置策略模型，并对航空公司相应收益与旅客满意度变化之间的关系进行定义。最后，在以上模型建立与分析的基础之上，以深圳宝安国际机场T3航站楼为仿真对象，运用Anylogic软件来模拟大面积航班延误情境中航空公司处置措施对旅客情绪的影响效果，从而为有效防控旅客群体性事件提供方法。

1 航班延误航空公司处置策略模型

1.1 模型建立

现假设有一个航线航班由航空公司Ai提供(i=1,2)，其中航空公司A1代表定位于中高端旅客的传统全服务型航空公司，此类航空公司追求品质、注重旅客体验，市场占有率高、机队规模大且航班密集；而航空公司A2则为低成本航空公司，其重点满足消费者对于出行服务经济、便利的需求，通常使用单一机型与单级舱位，同时其主要特色为低票价且无附加服务。以航空公司A1和A2为参与主体建立了博弈模型，表1所示为博弈双方的收益矩阵。

表1 航空公司处置策略博弈收益矩阵

如表1所示，其中，M1表示航空公司恢复航班/提供退改签服务，该措施对于旅客的情绪具有快速、显著的提升效果；M2表示航空公司提供餐饮休息服务/经济补偿，该措施可以在刚实施的一段时间内缓解旅客因航班延误而产生的不满情绪，但随着航班延误时间的不断增加，其作用效果也会逐渐减弱。

在该博弈中，对其收益矩阵做如下假定：航空公司A1和A2的收益相当，均设定为R；当航空公司A1和A2均选择策略M1时，则存在飞机油耗以及调机费用等成本，将该运行成本设定为C1；当航空公司A1和A2均选择策略M2时，将为旅客提供的食宿成本或经济补偿假设是C2；若航空公司A1与A2各采取M2与M1，则前者那部分迫切需求出行的旅客会产生不满情绪，旅客的满意度下降，航空公司A1因此而产生的损失设定为L，而航空公司A2由于积极恢复航班来避免间接影响产生的损失，将其假设是K。同样，航空公司A1与A2各采取M1与M2，则后者虽有部分迫切需求出行的旅客会产生不满情绪，但由于低成本航空公司本身性质及定位的原因，航空公司A2因此而产生的损失会比较少，暂且忽略不计，而航空公司A1由于积极恢复航班来避免间接影响产生的损失，把其假设是K。根据上述的设定能够知道：C1>C2，K>L，同时R、C1、C2、L、K全部为正值。

定义A1与A2采取策略M1的概率分别为x和y，则A1采取策略M2的概率为1-x，A2采取策略M2的概率为1-y。采取M1、M2策略的航空公司A1边际期望收益值为

U11=y(R-C1)+(1-y)(R-C1+K)

(1)

U12=y(R-C2-L)+(1-y)(R-C2)

(2)

航空公司A1的期望收益为

U1=xU11+(1-x)U12

(3)

同样，采取M1、M2策略的航空公司A2边际期望收益值为

U21=x(R-C1)+(1-x)(R-C1+K)

(4)

U22=x(R-C2)+(1-x)(R-C2)

(5)

航空公司A2的期望收益为

U2=yU21+(1-y)U22

(6)

参考这些结果，可以列出相对应的动态方程。A1选择M1的增长率动态方程为

(7)

A2选择M1的增长率动态方程为

(8)

对式(7)和式(8)改写为

(9)

式(9)中：Mx=-(K-L),Nx=C1-C2-K,My=-K,Ny=C1-C2-K。

因此，策略平衡点分别是：Ο(0,0)，A(0,1)，B(1,0)，C(1,1)。

该系统的Jacobian矩阵为

(10)

(1)若K+C2-C1<0。

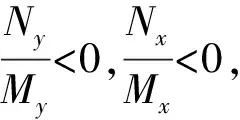
此时，航班延误下航空公司处置策略演化的复制动态关系能够以平衡点相图，如图1(a)所示，图S(x,y)为A1和A2之间的动态博弈过程。当K+C2-C1<0时，演化稳定策略只有点A(0,1)，即表示航空公司A1和A2经过长期反复博弈。

图1 复制动态关系图

(2)若K+C2-C1>0且C1-C2-L>0。

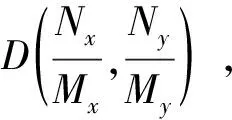
1.2 模型分析

由上述理论模型可知，于各种情景中，双方通过多次博弈会最终处于不同的演化稳定状态，同时，其最终策略由C1、C2与K及L的相互关系来决定。

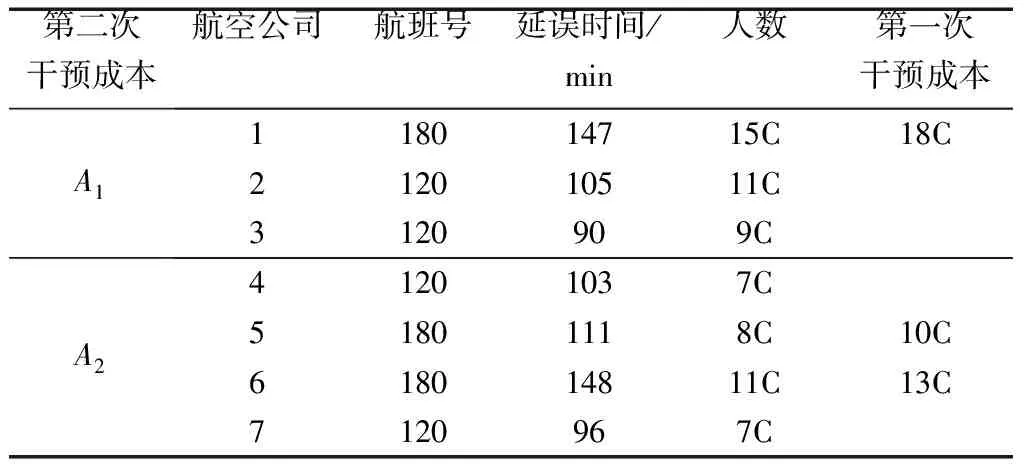
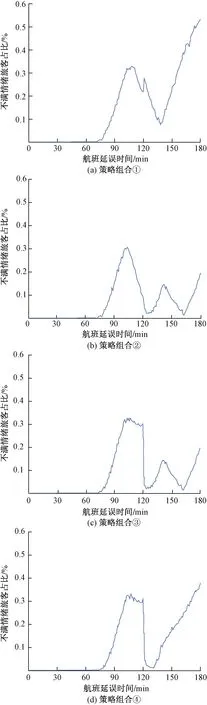
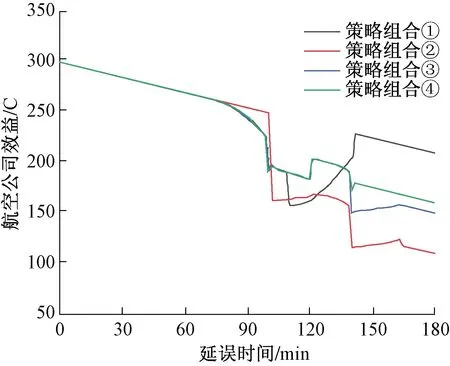
(1)在第一种稳定状态中，K+C2-C1<0，则R-C1+K

此时，(M2,M2)构成该博弈模型的严格纳什均衡，即在此种情况下，当航班延误发生时，各航空公司均会趋向于为延误旅客提供餐饮休息服务或经济补偿以安抚旅客情绪。

在这种情况下，各航空公司的旅客得到的服务体验是类似的，其满意度均会在一段时间内有所提升，但是随着航班延误时间的不断增长，这些安抚举措的作用也会逐渐减弱，旅客群体中不满情绪的旅客数量又会有所提升，因此需要加强后续的干预，防控群体性事件的发生。

(2)在第二种稳定状态中，K+C2-C1>0且C1-C2-L>0，则R-C1+K>R-C2且R-C2-L>R-C1。

此时，(M2,M1)构成该博弈模型的严格纳什均衡，即在此种情况下，当航班延误发生时，传统全服务型航空公司将趋向于为延误旅客提供餐饮休息服务或经济补偿，而低成本航空公司则会趋向于恢复航班或给延误旅客提供退改签服务以安抚其情绪。

在这种情况下，首先由于采取措施的差异，各航空公司的旅客之间会产生服务体验落差，其满意度均会受到其他旅客接受的服务价值的影响，因此可以通过提高服务质量、增加经济补偿等手段，从而提升旅客满意度、稳定旅客情绪。其次，由于不同航空公司性质与定位的不同，以及相应旅客期望和容忍水平的差异，各航空公司之间也应当统筹规划，确定合理的策略组合，从而有效且经济地防控群体性事件的发生。

2 仿真实验及结果分析

2.1 仿真场景描述

结合目前已有基于智能体的相关仿真建模方法研究[10-12]，在上文对大面积航班延误情景下旅客满意度以及航空公司相应处置策略的研究基础上，以Anylogic仿真软件作为仿真平台，构建枢纽机场大面积航班延误情景下航站楼候机区内群体旅客的虚拟场景。

据相关数据显示，2019年深圳宝安国际机场实际出港航班量为17.19万班次，出港运力同比增长8.09%，出港准点率为73.71%，起飞平均延误32.72 min。参照去年四月份发生的大面积延误，选择10架航班的相关讯息(进行仿真实验时只保留其位置，对于实际起飞时间等信息则根据实验时的具体需求进行另外设定)。

然后，把这些航班放到实际航站楼出发层中去，得到其登机口分布情况，为便于实验与分析，不妨把该具体分布图进行简化，结果如图2所示。

图2 简化版登机口分布图

2.2 情景假设及实验模拟

假设航班1～3是属于同一航线的航班，且由航空公司A1提供，而航班4～7是属于另一航线的航班，且由航空公司A2提供。根据已建立的航班延误处置策略模型及相关讨论分析结果，不妨假设各类成本、损失及收益之间的关系满足条件K+C2-C1<0,即处于第一种稳定状态中，此时若大面积航班延误发生，则各航空公司均会趋向于为延误旅客提供餐饮休息服务或经济补偿以提升旅客满意度、安抚旅客情绪，从而防止群体性事件的发生。

考虑到实验操作性并研究各策略组合下的实验结果，假设该7个航班同时发生延误，持续时长均已知。现对各航班的人数、延误时间及干预成本、各航空公司的不同策略组合进行假定，如表2所示。

注：干预成本的设定与航空公司定位及航班属性等因素有关，为便于研究与分析，且使得各策略组合的成本大小更加直观，不妨用符号代替具体成本，如表2中，C为单位成本，通过其前面的系数来衡量不同航空公司对不同航班的干预成本大小。

表2 各航班人数、延误时间及干预成本设置

不妨设置若做到有效防控旅客群体性事件的发生需要将不满旅客人数控制在总人数的35%以下(该数值只为结果分析设置，具体值还由其他各方面因素决定)，故将实施干预的时间节点进行如下设置。

策略组合①：当航空公司A1、A2均分别在航班延误发生至100 min、110 min时对延误时长为2 h、3 h的航班旅客提供餐饮休息服务或经济补偿以安抚旅客情绪。

策略组合②：当航空公司A1、A2均分别在航班延误发生至100 min时对延误时长为2 h、3 h，140 min时对延误时长为3 h的航班旅客提供餐饮休息服务或经济补偿以安抚旅客情绪。

策略组合③：当航空公司A1、A2均分别在航班延误发生至100 min、140 min时对延误时长为3 h的航班旅客提供餐饮休息服务或经济补偿以安抚旅客情绪。

策略组合④：当航空公司A1、A2均分别在航班延误发生至100 min时对延误时长为3 h的航班旅客提供餐饮休息服务或经济补偿以安抚旅客情绪，而航空公司A1在航班延误发生至140 min又再次对延误时长为3 h的航班实施干预举措时。

2.3 实验结果及分析

各策略组合下不满情绪旅客人数占比的变化情况如图3所示。

图3 实施不同策略组合时不满情绪旅客占比变化

而各策略组合下的航空公司效益(收益-成本)如图4所示。

图4 实施不同策略组合时航空公司收益变化

接下来，针对上述四组仿真实验结果进行如下几点分析及讨论。

(1)首先，当航空公司A1、A2采取策略组合①时，此时无法把不满情绪旅客人数控制在35%以下，从图3(a)中可以清晰地看见，当工作人员的干预结束后，不满情绪旅客人数又呈现增长态势。因此，若是航空公司单单只让其工作人员干预一次就放任不管显然也会激化旅客情绪，从而很有可能导致群体性事件的发生。该实验结果表明，航空公司应当及时采取有效措施，尽可能早地将旅客情绪控制在稳定状态，否则就会使整个形势变得更加严峻，之后便需要花费更多的各项成本才能够安抚旅客，以防群体性事件的爆发。

(2)因此为了有效防控旅客群体性事件的发生，在策略组合②中，当航班延误发生至140 min时，航空公司A1、A2均对延误3 h的航班进行二次干预，从图3(b)中可以清晰地看见，此时不满情绪的旅客占比被控制在30%以内。该实验结果表明，航空公司应当对延误时间较长的航班予以充分重视，在必要时可以实施多次干预举措，但产生的成本也会随之增加。

(3)于是为了降低成本，在策略组合③中，航空公司A1、A2均不再对延误时长为2 h的航班实施干预，而是令其对延误3 h的航班实施两次干预。实验结果表明，如果为了降低成本，航空公司可以选择优先对延误时间较长的航班实施干预，从而达到更加经济有效的控制效果。

(4)而为了进一步降低成本，在策略组合③的基础之上，策略组合④是令航空公司A2仅在延误进行至100 min时对延误3 h的航班实施一次干预。实验结果表明，当为了使总成本最小时，可以令不同类型的航空公司采取不同的手段策略，达到整体上的策略最优组合。但是从图3(d)中可以发现，在航班延误结束之前的一段时间内，不满情绪旅客占比不断攀升，若是延误时间不止3 h，则旅客情绪很有可能不受控制。因此在考量成本的同时依然不能放松警惕，还是应当谨防群体性事件的发生。

此外，根据上述航班延误处置策略模型的分析结果可知，采取措施的差异性也会对旅客情绪产生一定的影响。因此，在策略组合②的实施结果(图5)中，选择了旅客人数相似且各具代表性的两个航班：航班2、4进行分析，其中，航班2(105名旅客)有一个相邻航班，而航班4(103名旅客)没有相邻航班。这两个航班中不满情绪旅客人数占比的变化情况如图5所示。

图5 实施策略组合②时航班2、4不满情绪旅客占比变化图

对实施策略组合②时，航班2、4的实验结果进行对比分析，可以发现，由于航班4没有相邻航班，其旅客不会受到其他航班处置措施的影响，因此不满情绪旅客占比上升较慢，且最终占比较少。而航班2的旅客则由于相邻航班的存在，其情绪值增长较快，表现为不满旅客人数占比上升速度较快且占比较高。因此，在大面积航班延误发生时，可以在条件允许的情况下，对延误航班进行适当的隔离，从而稳定旅客情绪，有效防控群体性事件的发生。