桥梁钢-混结合段试验模型加载多目标优化
2021-08-03温伟斌伍彦斌曾文宋武黄方林
冯 帆,温伟斌,伍彦斌,曾文宋武,黄方林
(中南大学土木工程学院,长沙,410075)
混合式叠合梁斜拉桥由钢和混凝土两种材料组成,结合两种材料的力学性能,适合大跨度桥梁。钢-混结合段是混合梁斜拉桥的关键构造之一,是边跨和中跨两种梁体内力传递和变形协调的关键,中外有关专家学者对此开展了深入研究。目前,就钢-混结合段多采用模型试验与有限元计算相结合的方式进行研究,主要探讨结合段的受力与传力机理[1-5]。由于钢-混结合段构造复杂,采用有限元分析可以对其受力分析进行预测[6-9]。通过模型试验分析,可对钢-混结合段设计时的参数选取提供依据[10]。
近年来智能算法优化在各工程领域应用广泛,其得出的多个非支配解便于选取最合适的解[11-14]。遗传算法用于桥梁工程优化设计,使桥梁截面设计更为合理,以减少工程造价[15]。大跨径桥梁由于多种因素的影响,难以确定成桥状态,可以采用智能算法对线形进行预测,更好的保证施工质量[16]。桥梁结构损伤识别,采用遗传算法优化,可提高识别效率[17]。斜拉桥为高次超静定结构,其索力优化研究可使用遗传算法[18-19]。
目前,尽管遗传算法在很多领域得到广泛应用,但优化问题多为2个目标函数,且在桥梁模型试验中鲜有报道。对遗传算法在桥梁模型试验中的应用进行探讨。红水河大桥钢-混结合段内部结构复杂,存在应力集中及刚度突变现象,且结合段内力和变形情况无法准确地由有限元分析直接获得,需结合模型试验分析才能保证设计的可行性。模型试验的加载方式与加载力,需要通过模型设计,并保证其与实桥受力状态一致来确定。为了保证试验缩尺模型加载时受力与实桥相似,建立红水河特大桥全桥ANSYS模型,提取结合段关键截面内力,根据相似原理,计算试验缩尺模型中相应位置的内力,并建立结合段力学方程。根据截面内力及力学方程,建立四个目标函数的数学模型。利用MATLAB编程,采用多目标遗传算法对数学模型进行优化,解出最优的加载位置及大小,用于模型试验加载。
1 力学模型概述
钢-混桥梁结合段试验模型及其加载可以简化为图1所示的模型。模型试验不是针对某个细节构造的研究,所针对结合段模型试验的研究选择从整体出发。模型试验的加载方式与加载力,需要通过选取结合段中具有代表性的特殊截面,并保证这些截面的受力与实桥一致的前提来确定。
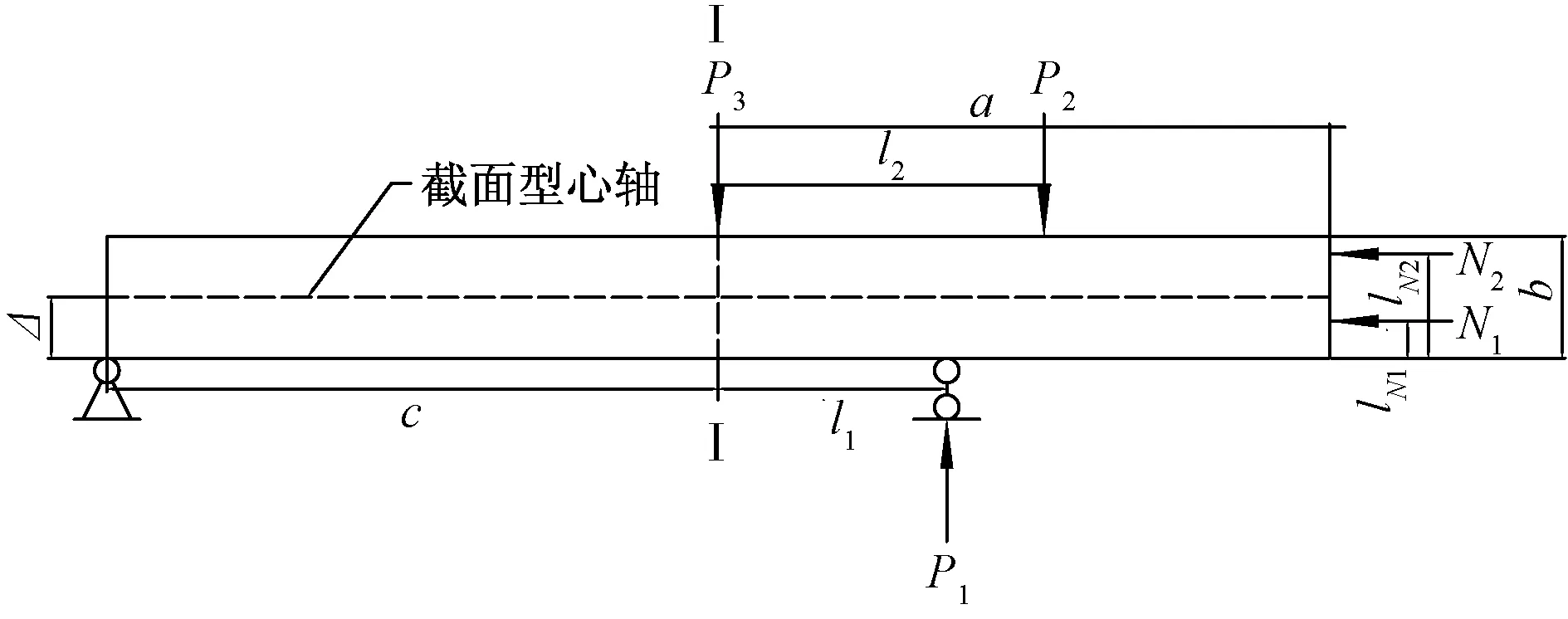
P1为支座反力;P2、P3为加载力;N1、N2为钢梁末端轴力,截面Ⅰ-Ⅰ为钢-混结合面;l1、l2分别为P1、P2到截面Ⅰ-Ⅰ的距离;lN1、lN2分别为N1、N2作用点位置到梁底的距离;Δ为截面形心轴到结合段底面的距离;a为钢-混结合面到结合段右端的距离;b为结合段的高度;l为结合段长度
2 优化模型的建立与分析
2.1 优化模型的建立
图1中,Δ、a、b、c、l1、lN1尺寸与N2轴力为已知常量,P1、P2、P3、l2、lN2为未知变量。为使钢-混结合面理论计算内力(轴力、剪力、弯矩)与实桥结合段内力结果相近。本文中采用理论内力与实桥结合段有限元计算结果的差值作为目标函数,且希望二者的差值最小,即
(1)
式(1)中:V、Ny、Fsy、My分别为目标函数、截面Ⅰ-Ⅰ轴力、剪力、弯矩有限元计算结果。Nl、Fsl、Ml的计算公式可分别表示为
(2)
根据图1中的信息,且轴力方向向右为正值与荷载方向向上取正,得到约束条件为
(3)
2.2 优化算法的选取
根据上节内容可看出,本问题属于有多约束的多目标优化。多目标优化问题,一般采用传统的加权法与目标规划法解决。但传统方法在解决多目标优化问题时,计算结果往往得到目标函数的局部最优解,而无法得到全局最优解。遗传算法是模拟生物进化的一种全局优化算法,优化时搜索性、鲁棒性强,且计算效率高。基于遗传算法的优点,本文选用遗传算法来解决钢-混结合段加载优化问题,具体流程图如图2所示。
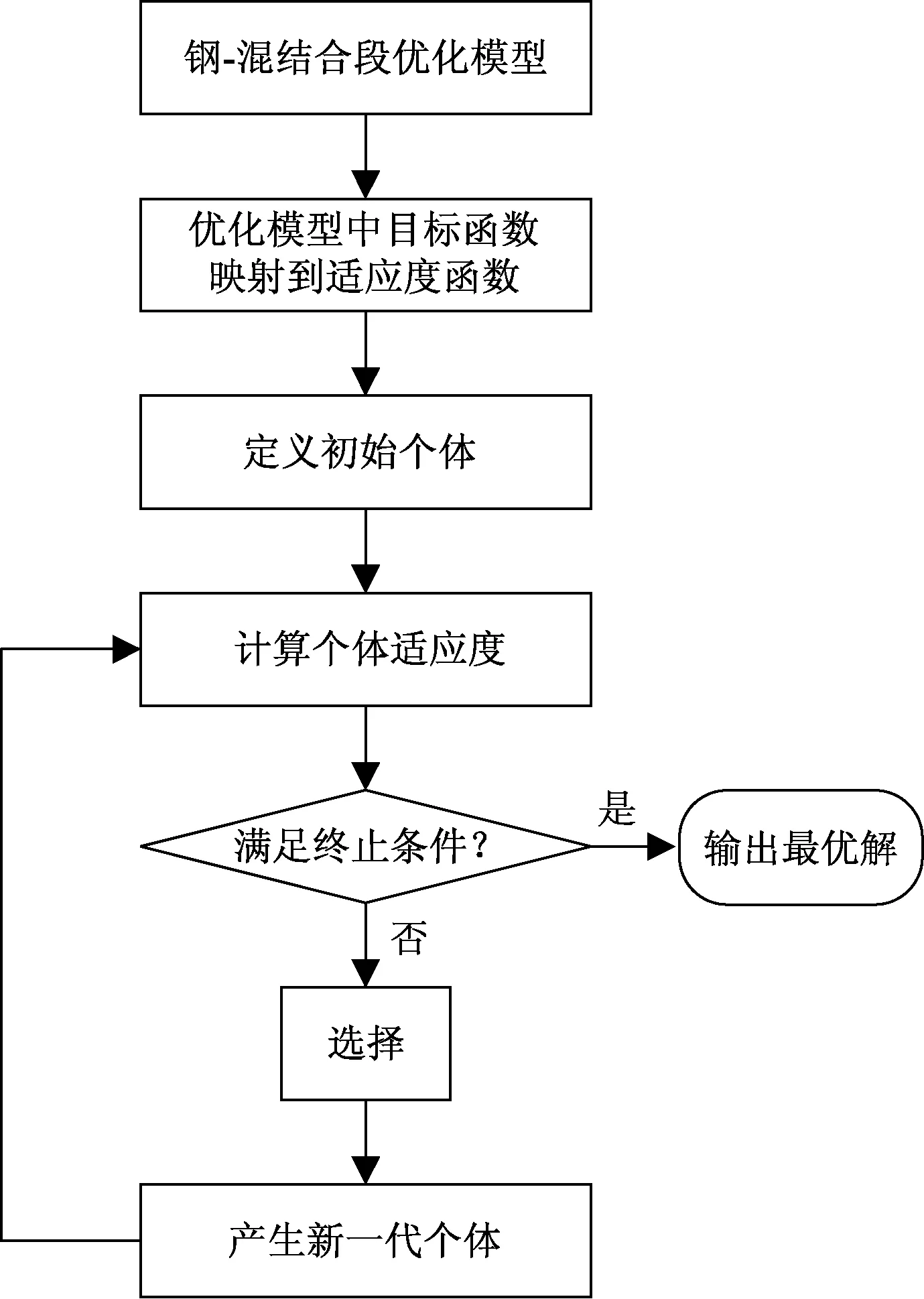
图2 遗传算法流程图
2.3 优化模型分析
在使用遗传算法对钢-混结合段缩尺模型加载优化时,具体实施过程如下。
(1)按照式(1)~式(2)推出目标函数,即需要控制截面的轴力、剪力与轴力。
(2)根据式(3)制定目标函数中变量的约束条件。
(3)将目标函数与约束条件编辑为函数并嵌入已编好的MATLAB遗传算法优化程序。
(4)调整遗传算法优化程序中各种参数,如群体大小、交叉概率、迁移概率、终止条件等。
(5)运行程序优化函数,得到优化结果。
(6)由于遗传算法优化结果较多,且存在部分早熟解,故需制定选取原则,并从优化结果中选取最合适的解。
3 案例分析
3.1 有限元模型与缩尺模型
红水河大桥是贵州省第一座采用混合叠梁的大跨度斜拉桥,简图如图3所示。钢-混结合段位于广西岸6号主塔中跨侧无索区,由端部承压板、钢主梁及加劲肋板、混凝土主梁、剪力连接件及预应力束组成,该结合段用于钢主梁向混凝土主梁刚度的过渡和荷载的传递。本节建立实桥有限元模型与缩尺试验结合段有限元模型,用于提取关键截面内力作为目标值。通过优化,确定缩尺模型试验的加载位置与加载力。
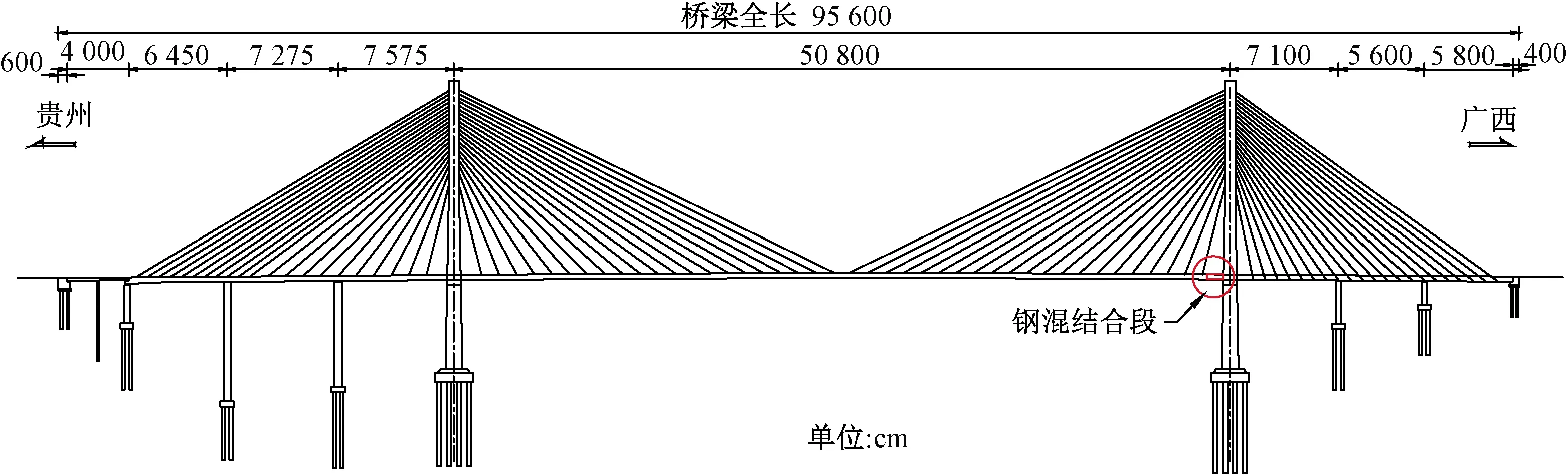
图3 红水河大桥简图
3.1.1 实桥有限元模型
首先建立实桥ANSYS模型如图4所示,采用Shell181单元模拟桥面板;采用Beam188 单元模拟各类纵、横向梁及主塔,在模型中考虑钢梁的加劲肋板、斜拉索锚固体系等构造的质量贡献;采用Link180单元模拟斜拉索,划分为多段杆单元以考虑垂度效应;采用MPC184刚性梁单元将斜拉索端部节点分别与主梁、主塔节点连接。加载时设置了一期恒载、二期恒载以及预应力。

图4 实桥有限元模型
由实桥有限元计算可以得到,钢-混结合面在轴压最大最不利荷载组合下,钢-混结合段中4个关键截面的内力(结合面两侧、埋入段中部与尾部),具体计算结果见表1。若要得钢-混结合段缩尺模型中对应的4个关键截面内力值,需根据相似原理结合缩尺比例来进行换算。缩尺模型和实桥钢-混结合段几何尺寸相似。其中,力的换算比例为1∶9,弯矩换算比例为1∶27。根据相似比换算后,各截面内力数值见表2。

表1 实桥钢混结合段4个关键截面的主要内力

表2 实桥完全相似到试验模型后的内力
3.1.2 缩尺模型
截取实桥钢-混结合段及其两侧主梁约14.2 m长范围,按相似原理设计制作了一个1∶3的试验模型(如图5所示),加上用于试验加载用的构造,模型总长5 m,宽1.05 m,高1.098 m。模型中钢梁的严格按照实桥尺寸1∶3选材,钢材使用Q345,弹性模量为210 GPa;模型中的混凝土使用C55强度,与实桥一致;剪力钉采用φ13 mm的栓钉,钢梁顶板所用栓钉长50 mm,其余部位所用栓钉长80 mm;主梁中采用的钢筋强度等级为HRB400,直径主要为12、16、20、28 mm;预应力筋采用与实桥结构中力学性能相同的φ15.2 mm高强度低松弛钢绞线。

图5 缩尺模型
3.2 钢-混结合段加载优化
基于表2,实桥相似到试验模型后的内力结果,开展优化研究。
3.2.1 优化模型
为了验证实桥钢-混结合段的工作状态,试验时,要保证缩尺模型关键截面的内力与实桥等比例相似。试验时,将模型考虑为伸臂形式加载。在加载时,随时调整预应力钢绞线张拉力的大小。优化时,将钢-混结合段4个关键截面的内力作为目标值,在保证钢-混结合面内力与实桥相似的基础上,确定加载的位置与大小,并尽量保证其他3个截面内力与实桥尽量相似。
试验中对模型张拉体内预应力钢绞线并锚固,体外预应力仅在试验时张拉。预应力主要使试验模型产生轴力与少量弯矩,加载示意图见图6。
加载时,将两个竖向力P2、P3加载在模型顶部,模型底部施加一个竖向力P1,模型钢梁侧的端部加载N1、N2模拟桥梁钢梁段传递的轴力。为了便于加载及减少试验变量,试验时,固定P1的位置与N2的大小。由于预应力钢束位置固定,故lN1不变。
对钢-混结合段4个截面的内力计算式如表3所示。

表3 各截面内力计算式
根据实际模型尺寸与试验实测结果得到T1=-156.2,T2=-4843.4,T1α1=-73.6,T2α2=253.9,G1=-29.2,G2=-49.9,G3=-66.2,G11=-37.7,G21=-64,G31=-95.1,Δ1=0.544,Δ2=0.667,Δ3=0.677,l1=0.65,lN1=0.42,N2=-900。
由整体有限元模型计算提取的结合段两端的内力(轴力、剪力、弯矩)经过相似比后,作为边界条件,施加在试验模型两端,可保证试验模型和实桥受力特性一致,故本节将以表2所列的各截面的内力值作为目标值,以结合面钢梁侧内力与混凝土侧轴力作为主要目标,其他截面的内力作为次要目标。
采用多目标遗传算法对试验模型静力加载工况进行优化。将主要目标作为目标函数,将次要目标加以限制作为约束条件,简化该多目标优化问题。目标函数为
Z1=|M1+95|
Z2=|FS1+325|
Z3=|FN1+4 731|
Z4=|FN2+10 656|
(4)
约束条件为
3.2.2 优化结果
本数学模型为4个线性目标函数,共计9个变量,既有线性等式、不等式约束,也有非线性约束。在计算模型时,本文考虑种群类型为双矢量,种族大小为60,创建适应度函数为非线性,突变函数与交叉函数选择约束相关,交叉概率考虑为0.7,迁移概率为0.2。
通过优化计算,得到60组Pareto fronts解,其结果在图7中的Pareto fronts的四维分布表示。
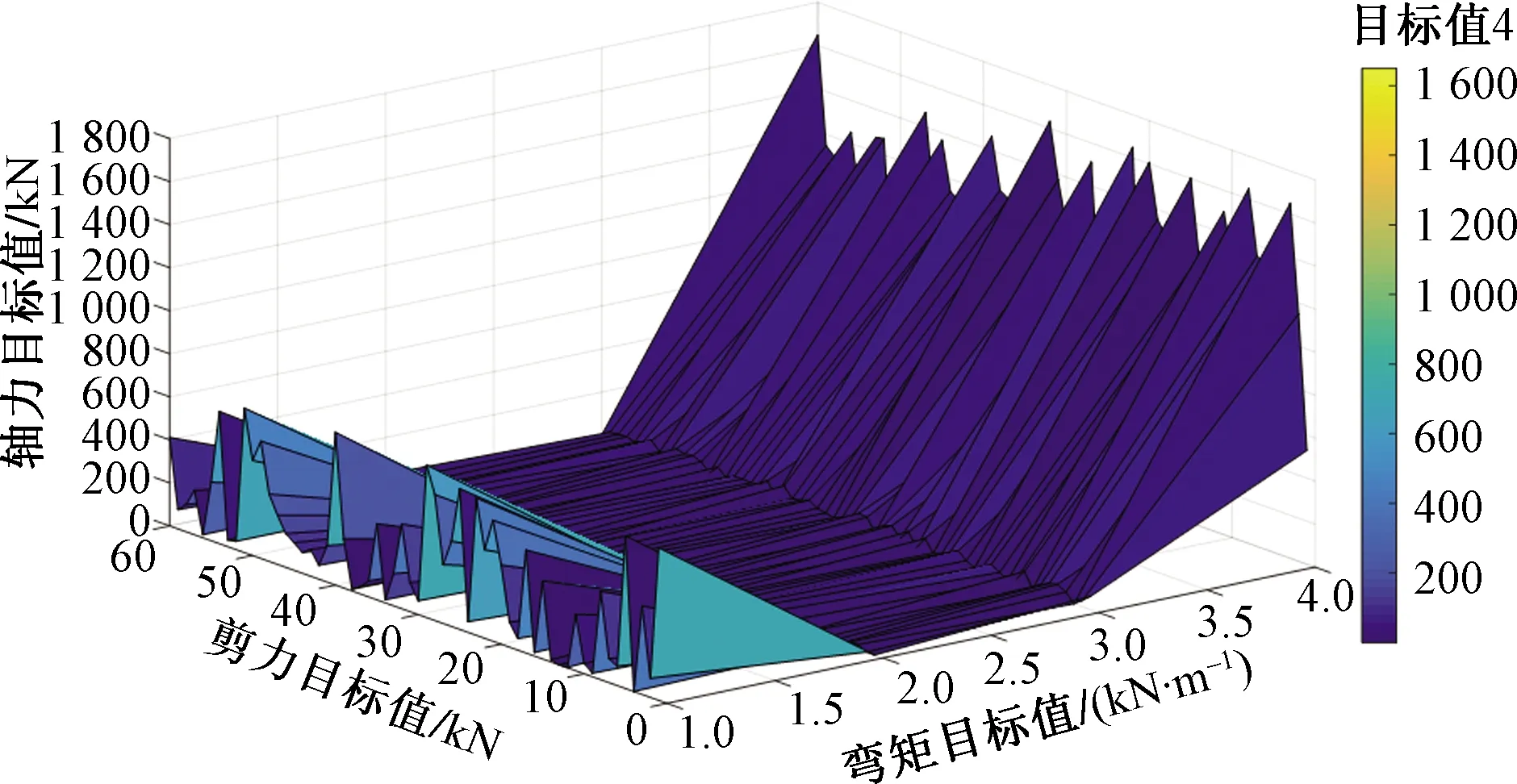
图7 4D-Pareto fronts分布
由于算法的初始种群是随机产生的,因此每次运行的结果并不完全一样,但是解的分布大部分会落在相近位置。为此,在优化结果选择时,考虑以下两点。
(1)确保轴力、剪力、弯矩正负号与有限元理论计算值一致。
(2)将优化结果代入表3的计算式后,选取和结合面钢梁侧、混凝土侧轴力目标值最接近的解集。
最终,得到优化后的各截面内力,选取的优化结果见表4。将优化结果代入表3中的计算式,分别得到各截面的内力值,计算结果见表5。

表4 选取的优化结果
根据表5中数据可以看出,优化结果各个截面的轴力、剪力与弯矩和有限元理论计算值吻合良好。在加载时,选用优化后的加载方案进行加载。

表5 目标值与优化后的关键截面内力的比较
4 结论
(1)基于遗传算法鲁棒性的优点,提出一种对混合梁斜拉桥钢-混结合段缩尺模型试验加载位置及荷载进行优化的方法,使加载后缩尺模型中内力与实桥相应位置相似。
(2)根据结构优化理论,以结合段钢梁侧轴力、剪力、弯矩与结合段混凝土侧轴力作为关键目标,其他截面内力作为次要目标,建立拥有四个目标函数且拥有多种约束条件的数学模型,并探讨数学模型中约束条件的合理性。
(3)使用遗传算法对数学模型优化,调整合适的优化参数并筛选优化结果,选取最为合适的解作为加载方案。优化后的加载方案,使模型的内力与实桥相近。
