考虑需求响应和储能的风水火联合系统经济调度

潘 华，姚 正，黄玲玲，梁作放，肖雨涵

(1.上海电力大学经济与管理学院，上海 200090；2.上海电力大学电气工程学院，上海 200090；3.国网山东省电力公司菏泽供电公司，荷泽 274000；4.国网上海市电力公司松江供电公司，上海 201600)

随着煤炭等不可再生能源的快速消耗，传统的能源结构已逐渐无法满足人们的日益需求，提高风电等清洁能源在能源结构中的比例成为当下研究的热点[1-2]。然而，由于风电出力对自然环境的依赖度极高，具有很强的随机性和波动性,其并网时会威胁到电力系统的稳定运行，无法实现独立稳定供能。同时，大量的弃风现象造成了能源的浪费[3-4]。风水火联合电力系统为解决这一问题提供了一条有效的途径，通过利用水电站的灵活性承担一部分的调峰任务，可以在有效地对风电等清洁能源出力消纳的同时提升电力系统运行安全[5]。

针对风水火电力系统的联合调度优化方法，中外学者从能源转换、储能系统及需求响应(demand response, DR)等方面展开了诸多研究，并取得了相应的研究成果。储能系统(energy storage system，ESS)以其低能耗、灵活性被广泛应用于联合电力系统中，通过转移能源的利用时间可有效地抑制风电等清洁能源出力的波动性[6]。文献[7]通过构建电池储能系统，有效协助多水库级联水电站对分布式电源的消纳，提升了风电等清洁能源的利用率。文献[8]利用抽水蓄能的方式来应对风电场出力的波动性，有效地降低了系统的弃风率及运行费用。文献[9]将储能系统与梯级水电站联合减少可再生能源的波动问题，通过日前确定水电站的发电量及储能系统的容量有效缓解了可再生能源的波动性问题，降低了能源成本。另一方面，DR作为一种从用户侧进行能源管理的方式，能够通过激励手段对价格敏感型用户的用电行为进行调节，有利于协助风电等清洁能源的消纳[10]。文献[11]提出将DR看成需求侧的备用容量，在发电侧预留发电装置备用容量，构建双向备用容量模型，促进了风能的消纳。文献[12]在模型中引入了DR，通过对用电负荷调节达到削峰填谷的作用，有效协助了对分布式电源的消纳，降低了系统的总发电成本。针对风电出力的不确定性，文献[13-14]为保证电力系统稳定运行，预留了一定的装机容量；文献[15]采用随机规划处理风电等可再生能源出力的不确定性；文献[16-17]利用模糊理论及概率方法处理风电不确定性。

对以上研究分析可知，在调整能源的使用时间上，DR和ESS装置能够起到类似的效用。但以上研究多集中于对DR或ESS单独作用效果的探索，少有学者对DR和ESS之间的有效配合进行分析。而DR及ESS各自的优化方式单一，且ESS装置在大量充放电时会产生大量的电能损耗和充放电管理费用。因此，考虑DR和ESS的互补特性对风水火联合电力系统的优化效果是一个值得深入探讨的方向。

鉴于此，现提出一种计及DR和ESS的风水火联合系统经济调度模型，充分考虑了DR和ESS之间的有效配合。模型将用电负荷划分基础负荷和可调节性负荷，考虑DR对可调节性负荷的调节作用，有效配合ESS装置运行；针对风电出力不确定性，通过建立鲁棒优化模型实现了风电出力全额消纳；以系统总运行费用最小为目标函数，其中包含了火电机组运行费用、水电站弃水惩罚费用、ESS充放电管理费用，分情景验证了模型的有效性。

1 需求响应模型

需求响应主要通过调度人员发出的电价信号引导价格敏感型用户调整用电行为，即：当电能充足时降低电价，引导用户增加用电负荷；当电能紧缺时提高电价，引导用户减少用电负荷。通过DR可以将用电负荷从用电高峰时刻平移到非高峰时刻，在此过程中，用电负荷的改变量可以看作“虚拟发电出力”，可用于提高联合电力系统灵活运行及风电出力消纳。

传统的DR主要利用经济学需求原理，采用需求响应弹性系数进行描述，具体的电力需求和价格之间的计算公式[18]可改进为

(1)

式(1)中：当i≠j时εij为互弹性系数，当i=j时εii为自弹性系数；pload,i为实施DR之前时刻i的用电负荷；Δpload,i为实施DR之后时刻i用电负荷的变化量；Qj为平时零售电价；ΔQj为DR实施后零售电价的变化量；δload为建立的模型中可调节性负荷占总负荷的比例。可建立DR实施后用电负荷的变化量模型为

(2)

为简化计算，参照文献[19]令不同时刻的互弹性系数为0，只考虑i时刻的自弹性系数，则简化后的电负荷变化量可描述为

(3)

2 风水火联合系统经济调度模型

2.1 目标函数

论文所建立的经济调度模型以系统总运行费用最小为目标，综合考虑了火电机组运行费用、水电站弃水惩罚费用以及储能装置充放电管理费用。建立具体目标函数为

minFS=FG+FH+FESS

(4)

式(4)中：FS为系统运行总费用；FG为火电机组运行成本；FH为水电站弃水惩罚费用；FESS为储能系统管理费用。

式(4)所提各项费用函数的具体模型表示为

(5)

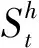
2.2 约束条件

模型建立的考虑ESS和DR的风水火联合系统经济调度模型的约束条件主要包括：功率平衡约束、风水火联合电力系统机组运行约束、储能系统约束、需求响应约束、系统备用容量约束等，具体描述如下。

(1)系统功率平衡约束。电力系统需要保证在各个时刻的功率保持平衡，为简化计算，建立忽略网损的系统功率平衡约束为

pload,t+Δpload,t

(6)

式(6)中：pm,t为第m个风电场在t时刻的出力；ph,t为第h台水电机组在t时刻的出力。

(2)火电机组运行出力约束。

pmin,i≤pi,t≤pmax,i

(7)

-pdn,i≤pi,t-pi,t-1≤pup,i

(8)

don,i,t≥di,t-di-1,t-1

(9)

(10)

(11)

式(7)为火电机组出力约束；pmax,i、pmin,i分别为第i台火电机组出力的上、下限；式(8)为火电机组爬坡速率约束，pdn,i、pup,i分别为第i台火电机组有功出力最大下降速率及最大上升速率；式(9)为机组启动的0-1约束；式(10)为第i台火电机组最小启停时间约束，Son,i,t为第i台火电机组的持续开机时间，Son,min,i为第i台火电机组的最小启动时间，Soff,i,t为第i台火电机组的持续关机时间，Soff,min，i为第i台火电机组的最小停机时间；式(11)为机组持续运行时间及持续停机时间约束。

(3)水电机组运行约束。

(12)

Vh,t=Vh,t-1+(Qin,h,t-Qout,h,t)Δt

(13)

Vmin,h≤Vh,t≤Vmax,h

(14)

Qmin,h≤Qh,t≤Qmax,h

(15)

(16)

式(12)为水电转换约束，ph,t为水电站机组出力，ωh,x(x=1,2,3,4,5,6)为水电转换系数，Vh,t为水电站的水库容量，Qh,t为水电站的水流量，pmax,h、pmin,h分别为水电站机组出力上下限约束；式(13)为水电站水平衡约束，Qin,h,t为入库流量，Qout,h,t为出库流量；式(14)为水电站库容约束，Vmin,h、Vmax,h分别为水库容量的下限和上限；式(15)为水电站发电流量约束，Qmin,h、Qmax,h分别为水电站水流量的上下限约束；式(16)为水电站弃水流量约束，Sh,t为水电站弃水流量，Smin,h、Smax,h分别为水电站弃水流量的上下限。

(4)储能系统运行约束。ESS中的储能装置根据自身的充放电特性，在应对可再生能源消纳、调峰辅助服务等方面有着很好的效果。ESS在用电负荷低谷时段充电，在用电负荷高峰时段放电。ESS的运行主要考虑储能充放电损耗及储能装置的物理规律，因此对ESS建模如下。

(17)

(18)

0≤SOCl,t≤1

(19)

式(17)为ESS中储能装置充放电功率约束方程，pch,l,t、pdis,l,t为储能装置充放电功率；pch,max,l、pdis,max,l为储能装置充放电功率的上限；ESSl,t为指示储能状态的0-1变量：当ESSl,t=0时为充电状态，当ESSl,t=1时为放电状态；式(18)为储能荷电状态约束，ηESS,ch、ηESS,dis表示储能装置充电、放电效率；SOCl,t为储能荷电状态，EESS,l为储能装置容量上限；式(19)为储能荷电状态范围约束。模型中出现的D为引入的足够大的参数(大M法)。

(5)DR约束。DR用户会根据调度人员提供的电价信息来调整自己的用电负荷，但用户参与DR属于自愿行为，在用电时间上发生变化，却未改变周期内总用电量，同时也没有产生电能损耗。因此，在一个调度周期内需要保证可调整负荷总量维持不变，即

(20)

各时段电价约束为

λmin≤λt≤λmax

(21)

式(21)中：λt为优化后t时刻的售电电价；λmin为售电电价下限约束；λmax为售电电价上限约束。

(6)系统备用容量约束。为保证在考虑风电出力不确定的情况下，整个系统仍然能够安全稳定的运行，需要为系统预留一定的装机容量，即

(22)

(23)

式(22)为系统上旋转备用约束，其中R为旋转备用率，文中取10%；式(23)为系统下旋转备用约束。

3 优化模型的求解

3.1 风电出力不确定性建模

为应对风电出力的不确定性，常采用的方法有场景法、模糊法、鲁棒优化法。本文模型采用的是鲁棒优化法，通过构建不确定集合，保证在整个集合上模型都能够有可行解，实现了风电出力全消纳。所以本文模型的目标函数不计弃风惩罚费用，减少了由于弃风而带来的额外系统运行费用，符合本文所提的经济性。本文所构建的不确定集合Φ为

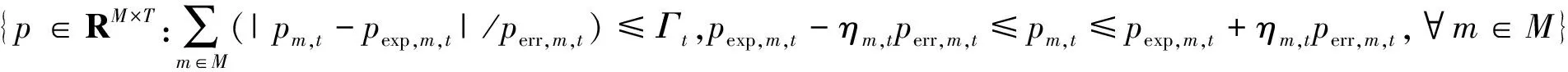
(24)

式(24)中：pm,t为第m个风电场在t时刻的实际出力；pexp,m,t为风电机组m在t时刻的预测出力；perr,m,t为风电机组出力误差；Γt不确定预算，根据决策者的决策赋值(Γt∈[0,M])；ηm,t∈[0,1]。

不难看出，以上建立的模型为双层模型，是由于式(22)、式(23)中含有max、min形式所导致的，无法直接进行计算，因此需要进行线性对偶变换，用式(25)、式(26)替换约束式(22)、式(23)。

(25)

(26)

式(25)由式(22)、式(24)进行线性对偶变换所得形式，αm,t、βm,t、χm,t、δm,t为经过对偶变换后所对应的对偶变量；式(26)由式(23)、式(24)进行线性对偶变换所得形式，ωm,t、ξm,t、φm,t、φm,t为经过对偶变换后所对应的对偶变量。

3.2 模型求解方法

本文模型综合考虑了ESS装置和DR实施的相互配合对风水火联合电力系统的优化效应。调度人员需要在日前制定电价信息对可调节负荷进行调整，配合储能设备的充放电，力求系统总运行费用最低。本文模型是一个典型的混合整数非线性规划模型，在GAMS环境中调用ANTIGONE求解器进行求解。ANTIGONE求解器对于混合整数非线性规划问题可进行确定性全局优化，对于本文模型有很好的求解效果。

4 算例分析

4.1 基础数据

本文算例采用1个1 350 MW的水电站，设置4台水电机组；1个1 000 MW的储能系统，设置3台储能装置；10台火力发电机组，3个风电场，组成了一个含有风水火储的联合电力系统。表1～表5分别为水电转换系数、火电机组、水电机组、储能系统以及分时电价等相关参数信息。风电出力预测值如图1所示。算例设定：①水电站弃水惩罚成本为250元/(MW·h)；②用户用电负荷中的可调性负荷占总用电负荷的60%，电量电价自弹性系数为-0.3；③为保证储能系统有效运行，设定经过一个调度周期，ESS中各储能装置的储能荷电状态与初始值一致，设定初始储能荷电状态为0.4。

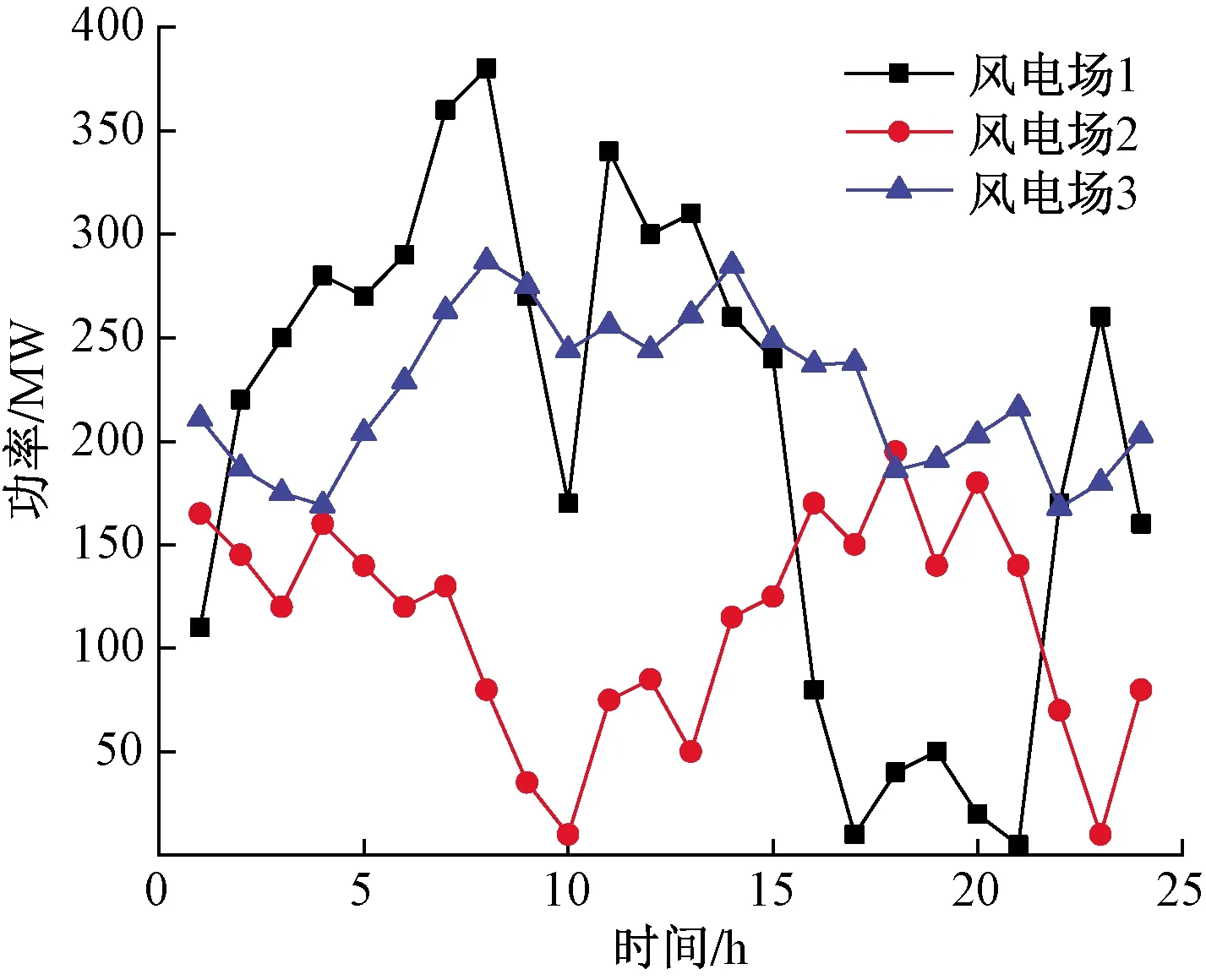
图1 风电出力预测曲线

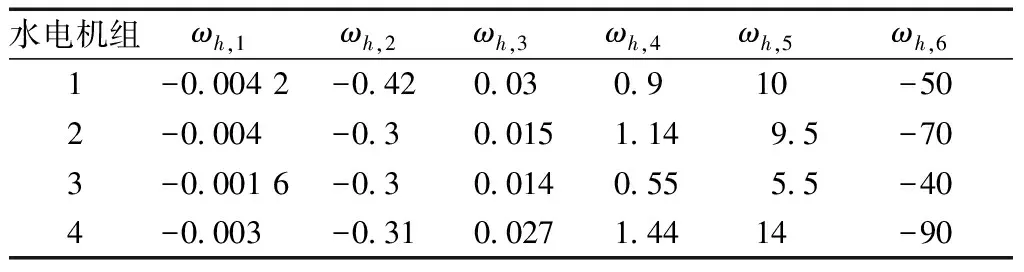
表1 水电转换系数

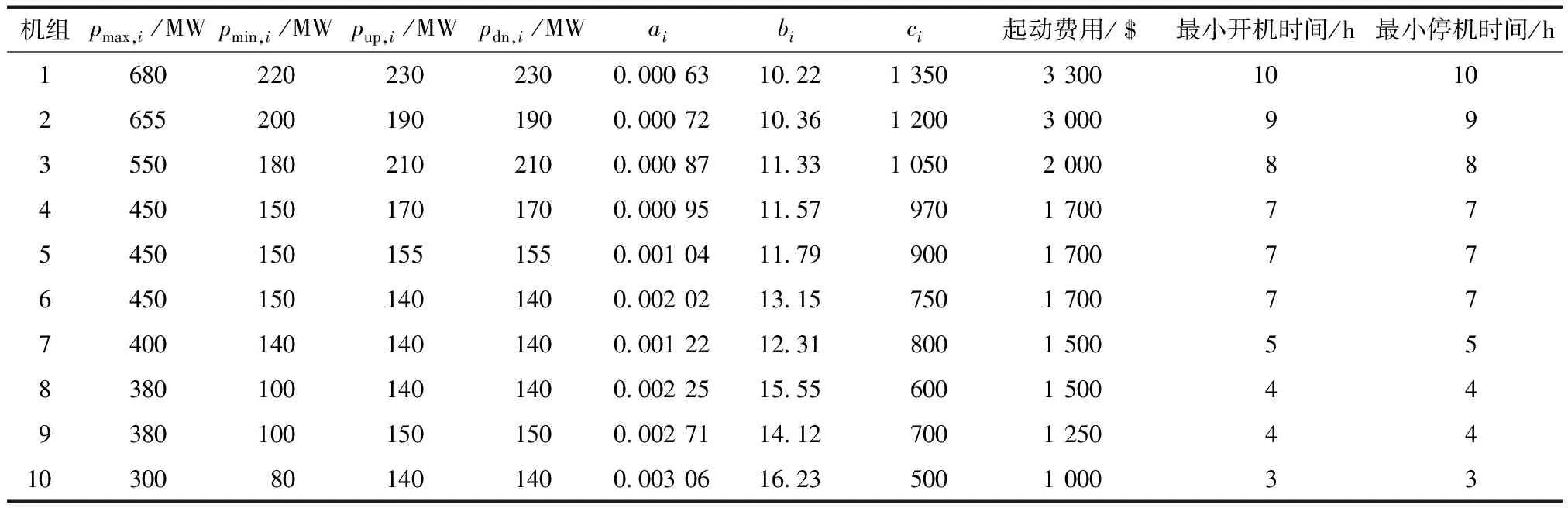
表2 火电机组参数

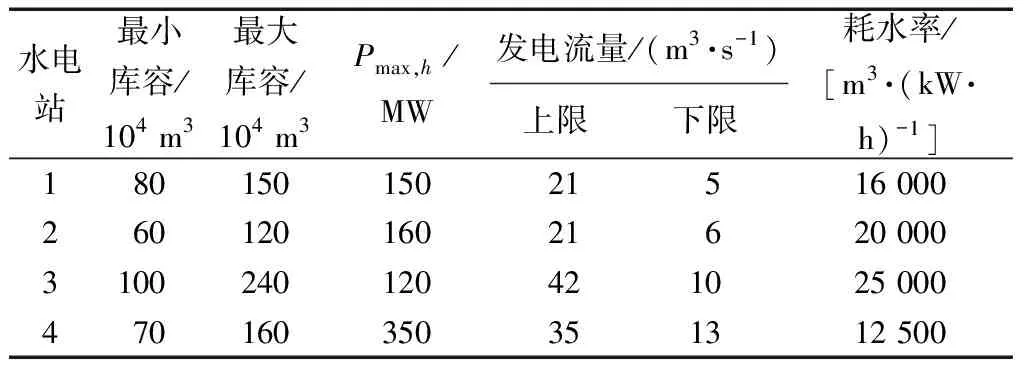
表3 水电机组参数

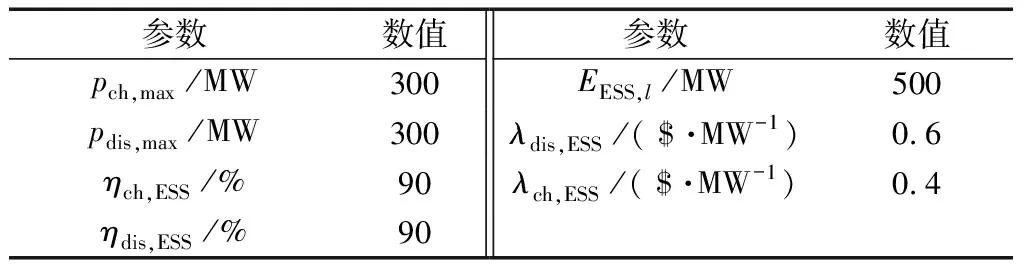
表4 储能装置基本参数

表5 不同交易时段的分时电价

4.2 情景设定

为分析ESS及DR对风水火联合电力系统运行的优化效用，设定四种场景分别讨论ESS及DR对风水火联合系统中火电机组运行的影响。

场景1：基础场景，只考虑了风水火联合电力系统运行时，为全额消纳风电出力，水电机组及火电机组的运行情况。

场景2：DR实施场景，该场景下，通过分时电价从用户侧对电能进行管理，调整用电负荷，分析DR对系统运行的影响。

场景3：含ESS场景，该场景下，系统中引入了ESS，通过分析引入ESS后的机组运行情况。

场景4：ESS和DR相互配合，该场景主要用于讨论DR和ESS有效配合对系统的优化效用。

4.3 算例结果

根据以上参数及情景设置，下面将分情景对本文所提的优化模型进行计算并进行相关分析。表6是不同情景下系统优化的结果。结合表6和图3～图5可知，情景2相比于情景1的系统运行总费用减少了0.67万元，这是因为DR的引入对用户用电负荷进行了调节，增加了火电机组运行的平稳性，减少了系统运行总费用。情景3相对比情景1的系统运行总费用减少了1.8万元，这是因为风水火联合电力系统中引入了储能系统参与风电出力消纳后，减少8、9、10号火电机组的启停，增加了火电机组运行的平稳性。情景4相比于情景2、3的系统运行费用进一步降低，是因为ESS及DR之间相互配合，在情景3的基础上，通过DR调整用电负荷实时对电能进行消纳，减少了对ESS的充放电。用户参与DR所调整的用电量是无损耗的，而ESS在电能的存储和释放上却存在一定的损耗，并且会增加系统运行成本。通过DR及ESS之间的有效配合，在增加火电机组运行平稳性及减少机组频繁启停的基础上，利用DR的负荷调节特性可实时消耗电能，减少ESS充放电带来的电能损耗、减少了ESS充放电所带来的额外的管理费用，从而大幅度降低了系统运行成本。下面通过系统内各设备具体运行情况进行分析。

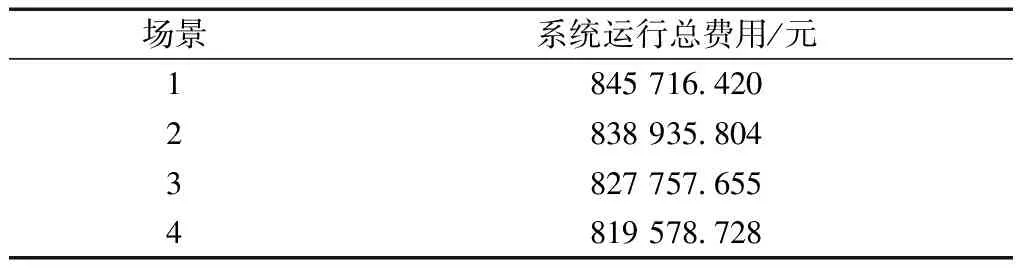
表6 不同场景下系统优化结果

1)场景1：基础情景结果分析

该情景用于分析风水火联合电力系统在应对风电出力的随机性和波动性时，火电机组和水电机组的运行情况，如图2所示。可以看出，水电机组在调峰方面具有一定的灵活性。

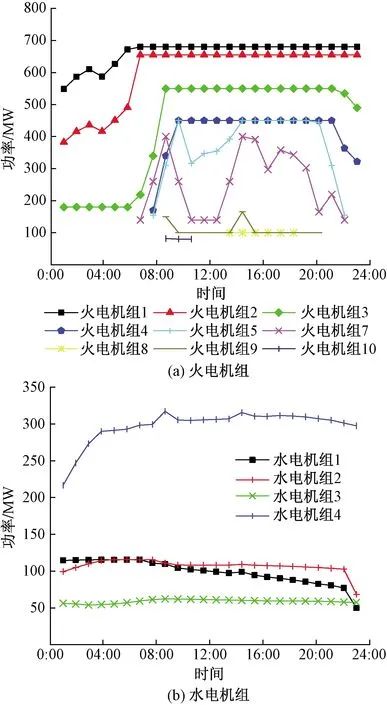
图2 场景1机组调度出力曲线

在01：00—06：00，用电负荷较低且变化较为平稳，通过水电机组的灵活性可以很好地承担部分调峰任务，同时火电机组出力变化较小。在07：00—16：00时用电负荷达到高峰，用电负荷及风电出力变化较大，水电机组由于受到水流流速及库容的影响无法急剧变化出力，这段时间主要通过变化火电机组出力来应对这种情况。火电机组的频繁启停及变化出力在增加了系统运行总费用的同时，也威胁到了电力系统的安全性和稳定性。

2)场景2：DR实施情景优化结果分析

情景2主要用于分析实施DR对机组运行的影响，如图3、图4所示。从中可以看出在01：00—06：00 时用电负荷较低，通过降低售电价格引导用户增加用电负荷，从而消耗在这一时段过剩的电能；在09：00—18：00时用电负荷波动较大，通过制定合理的电价，可平滑用电负荷曲线，减少火电机组出力的波动性。通过和场景1对比可以看出，实施DR后能够有效地降低机组出力的变化，此时，系统运行费用由845 716.4元降低为838 935.8元。

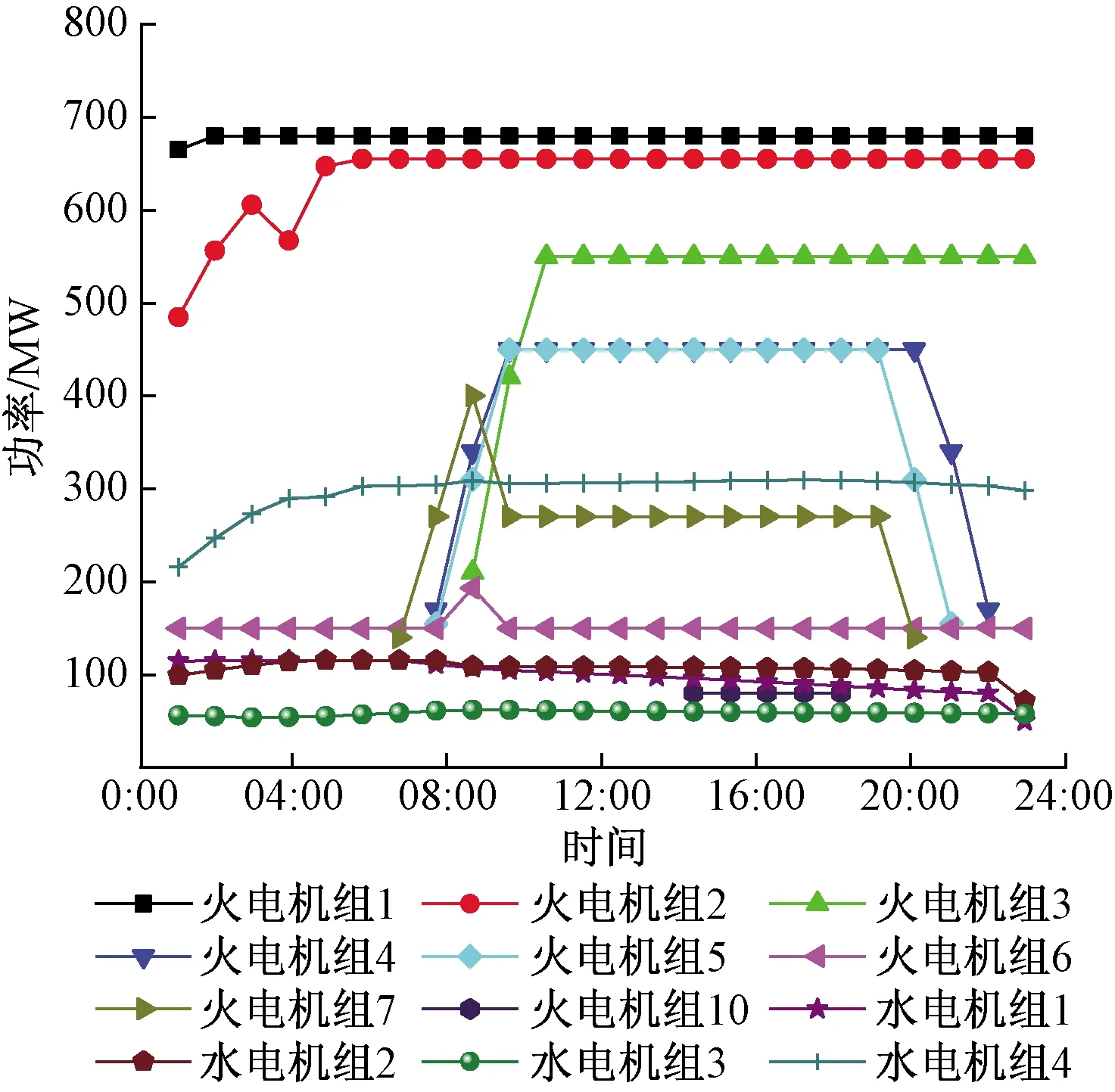
图3 场景2机组调度出力曲线

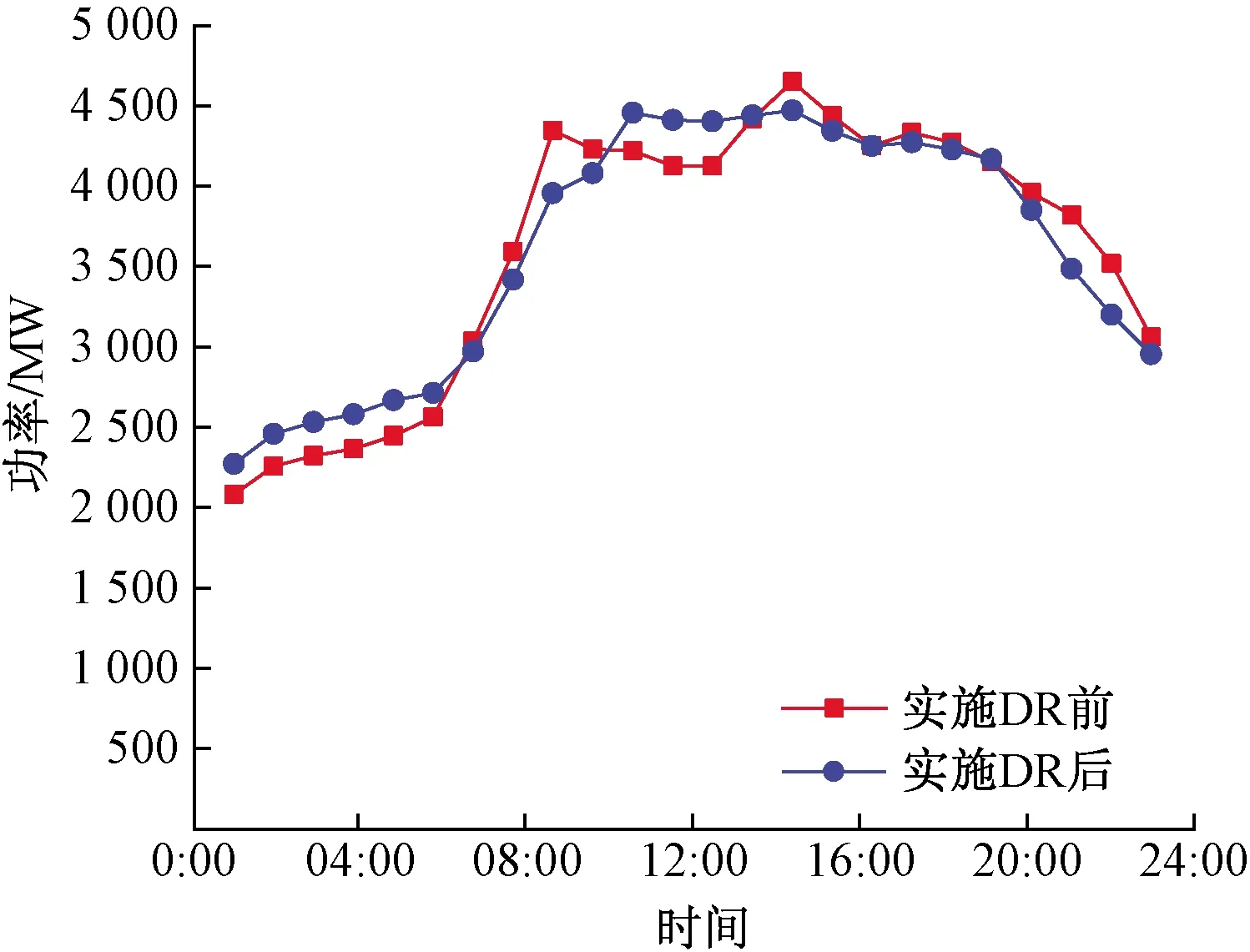
图4 场景2实施DR前后用电负荷曲线

3)场景3：含ESS情景优化结果分析

该情景主要讨论ESS对于联合电力系统运行的优化效用，图5、图6分别为引入ESS后机组调度出力曲线和储能系统的充放电情况。将图5和图2对比可知，引入储能系统后，火电机组出力波动性降低，且明显减少了部分火电机组启停。在 01：00—06：00时用电负荷较低，利用水电机组的灵活性可承担一部分调峰任务，同时风电出力较大又将过剩的电能储存在储能装置中。在07：00—16：00 时用电负荷达到高峰，水电机组灵活性受限，储能装置起到了主要的调节作用，通过储能装置放电弥补机组出力不足。这表明储能系统能够协助联合电力系统运行并对其进行优化，减少了启停火电机组所带来的额外费用，此时系统运行费用相比于场景1降低了17 958.7 元。

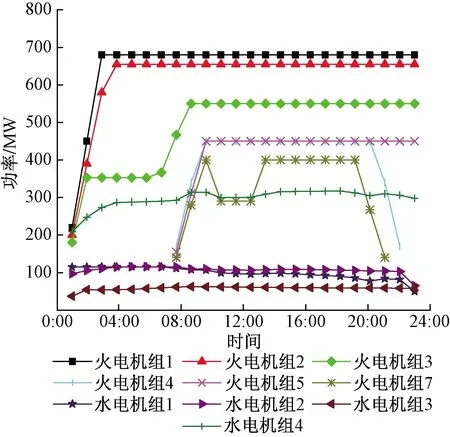
图5 场景3机组调度出力曲线

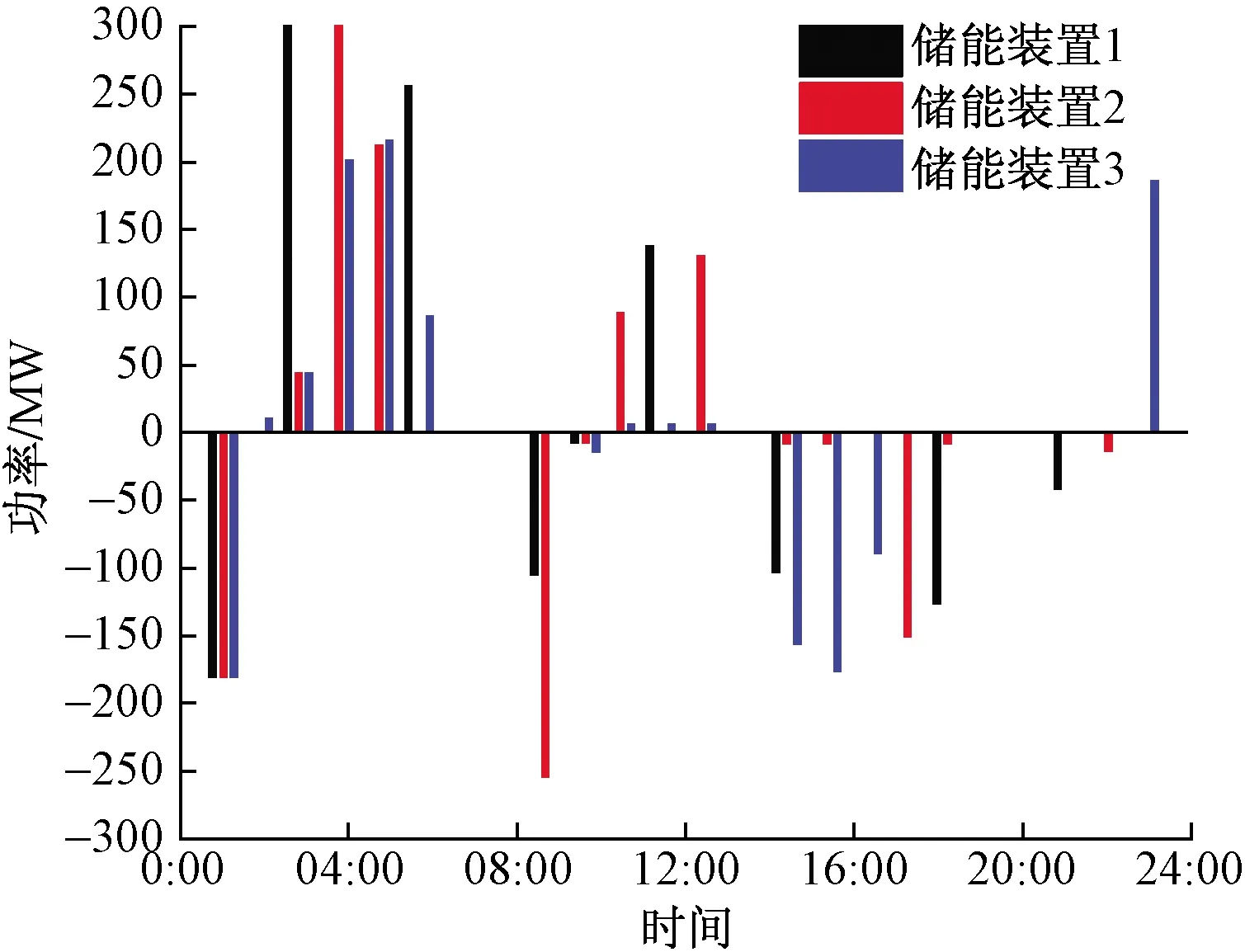
图6 场景3储能系统充放电情况

4)场景4：ESS及DR相互配合时优化结果分析

场景4主要用于分析ESS和DR有效配合时对系统的优化效应，如图7～图9所示。在01：00—06：00点时用电负荷较低，机组出力及风电出力较大，可通过制定分时电价，利用DR对用户的影响增加可调节负荷用电量，从而增加电能的消耗，减少对电能的存储。在07：00—16：00时，用电负荷达到高峰，一方面通过DR价格手段影响用户用电行为，对用电负荷进行整体优化，另一方面ESS则释放储存的电能。仿真结果表明，通过ESS和DR相互配合可有效降低系统运行总费用，减少火电机组出力波动，增加电力系统稳定性。场景4为最优运行场景，此时的系统运行费用下降最为明显，由场景1的 845 716.4 元降低为819 578.7元。

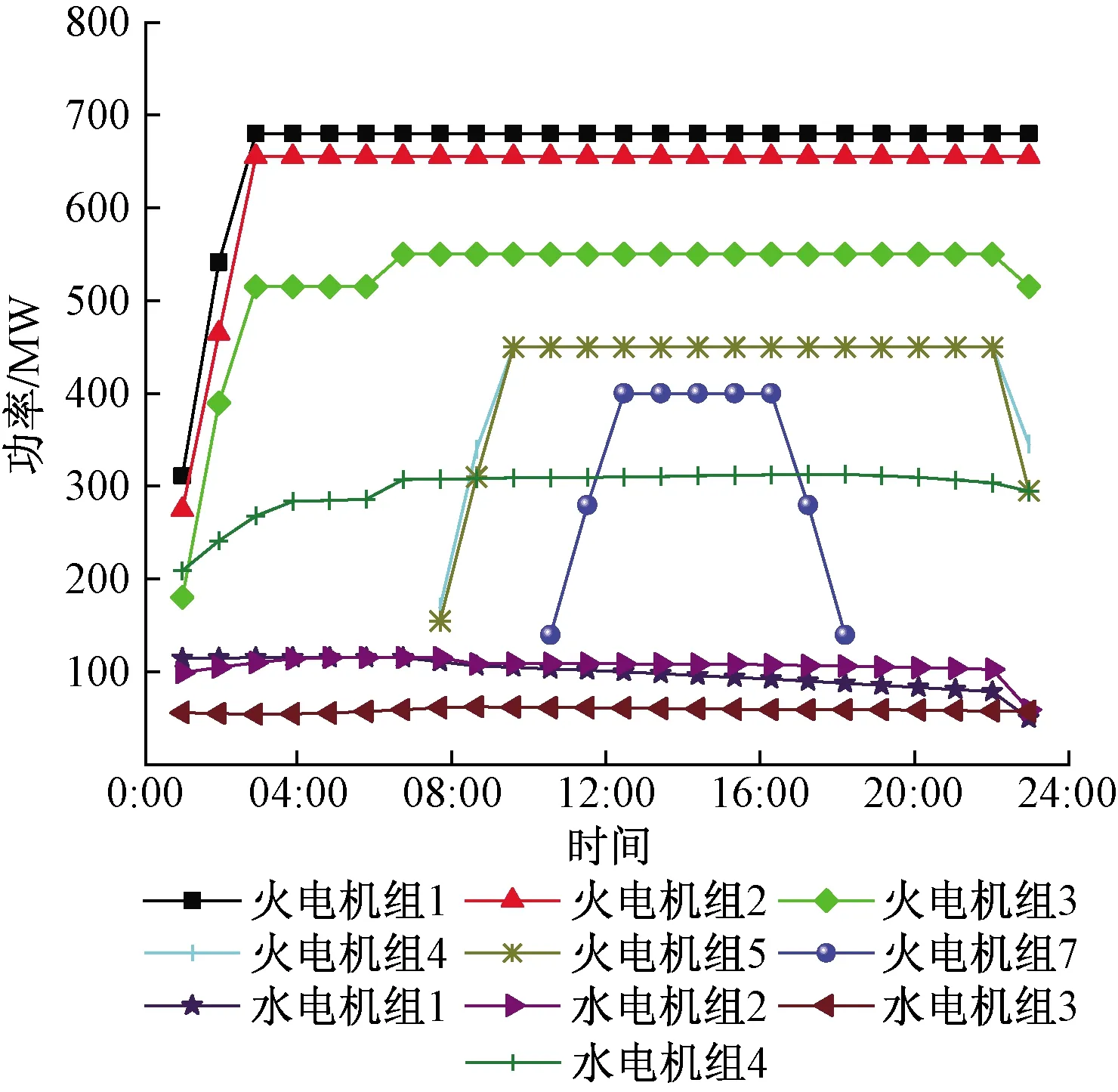
图7 场景4机组调度出力曲线

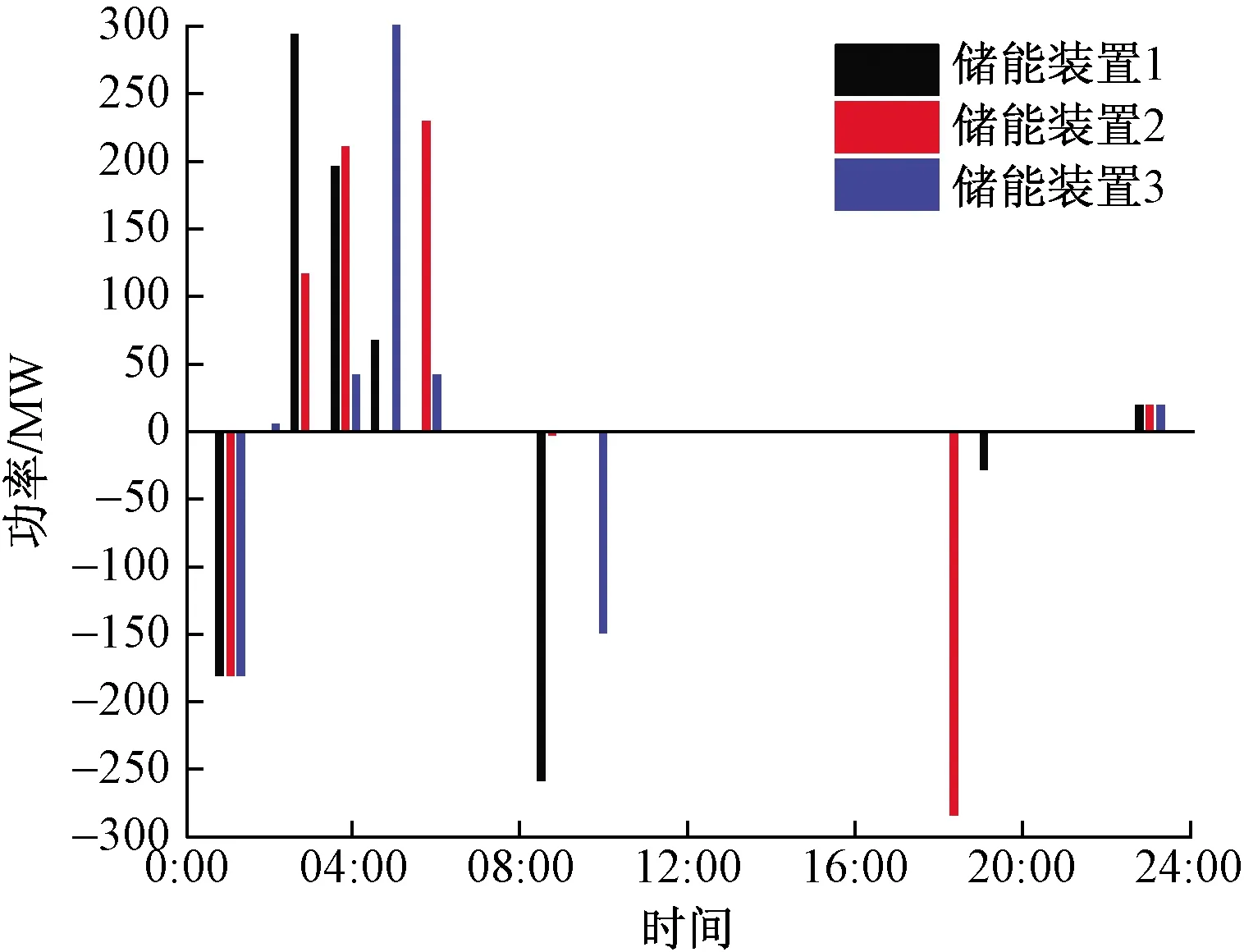
图8 场景4储能系统充放电情况

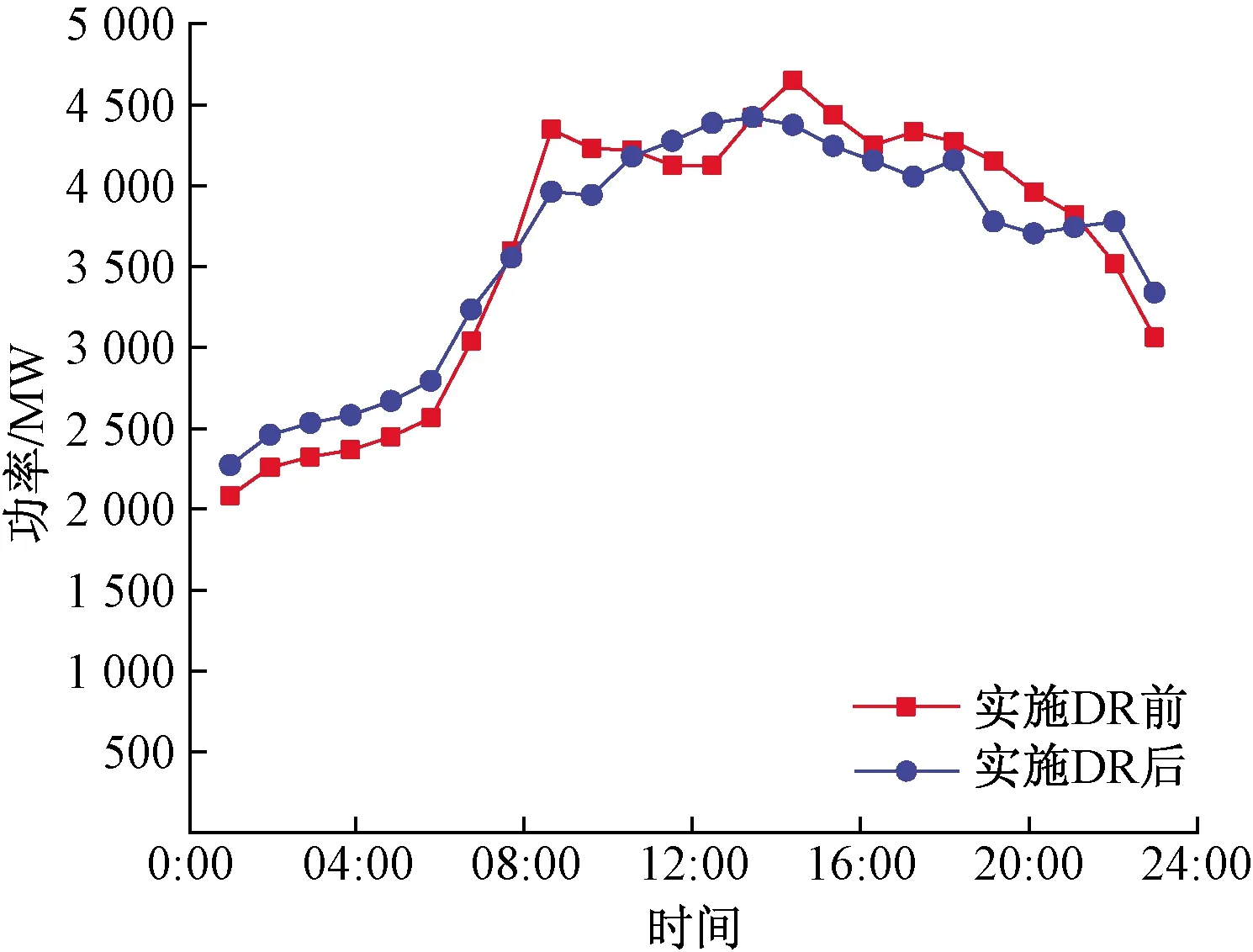
图9 场景4 实施DR前后用电负荷曲线

5 结论

研究了ESS和DR的有效配合对风水火联合电力系统的影响，提出了一种计及ESS装置和DR实施的风水火联合系统经济调度模型。采用鲁棒优化的方法考虑风电出力的不确定性，通过构建不确定集合保证论文所提模型在该集合中都有可行解，使得风电出力可全额消纳；通过旋转备用约束为系统留有一定的装机容量，保证系统能够可靠运行;将用电负荷划分为基础负荷及可调节性负荷，考虑DR应对用电负荷的调节作用，配合ESS对联合电力系统运行进行优化。最后通过划分不同的场景进行对比分析本文模型的有效性，仿真结果表明：

(1)DR作为一种从用户侧调节能源利用的方式，调度人员可通过日前的调度计划制定合理的电价来调整用电负荷曲线。

(2)DR在用电负荷较低时可通过增加用电负荷，减少过剩的能源存储在储能装置中，从而减少了电能存储在ESS中时造成的电能损耗及额外的管理费用。

(3)ESS和DR相互配合可以有效降低系统运行总费用，减少了机组频繁启停，平缓了火电机组出力的波动性，增加了电力系统运行的稳定性。