考虑非高斯相关噪声的视线角速率提取算法

张铎，宋建梅，赵良玉,*，焦天峰，丁国强

1.北京理工大学 宇航学院，北京 100081 2.中国兵器工业导航与控制技术研究所，北京 100089 3.郑州轻工业大学 电气信息工程学院，郑州 450002

捷联导引头因性能可靠、结构简单、成本低廉等优势，在空空导弹、反坦克导弹、制导炮弹、制导火箭弹等战术武器领域具有广阔而明确的应用需求。但是，由于捷联导引头只能敏感到目标与弹体轴线方向的角度关系，无法直接获取诸多战术武器制导所需的视线角速率信息。为了解决捷联导引头的视线角速率提取问题，国内外专家学者开展了广泛而深入的研究，并取得了丰富的研究成果。

姚郁和章国江[1]在将视线角与弹体姿态进行解耦的基础上，实现了捷联成像导引头视线角速率的提取。文献[2]建立了以视线高低角、视线高低角速率、视线方位角和视线方位角速率为状态变量的视线角速率估计模型以及全捷联导引头解耦模型，提出了基于扩展卡尔曼滤波(Extended Kalman Filter，EKF)的视线角速率提取算法。文献[3]提出了基于无迹卡尔曼滤波(Unscented Kalman Filter，UKF)的视线角速率提取算法，得到了更高的估计精度。文献[4]对状态变量进行扩充，增加了导弹与目标相对距离及其距离变化率两个状态变量，并利用五阶容积卡尔曼滤波(Cubature Kalman Filter，CKF)算法提取视线角速率，得到了较高的估计精度，但是弹目相对距离与弹目相对距离变化率这两个状态变量在只有角度观测情况下存在观测性弱的问题，对状态的估计精度和算法的稳定性会造成不利影响。文献[5]中提出了基于机载平台的修正球面坐标系目标跟踪模型，有效地改善了观测性弱的问题。文献[6]提出了修正极坐标系下的雷达与电子支援措施航迹对准关联算法，实现了雷达与目标之间的稳定追踪。上述研究均假设状态噪声与观测噪声为高斯白噪声且它们之间相互独立，这与真实场景下状态噪声和观测噪声的统计特性并不完全相符。

针对非高斯噪声条件下的视线角速率提取问题，文献[7-9]均采用粒子滤波(Particle Filter，PF)来提高视线角速率的估计精度，但是粒子滤波随着迭代次数的增加，容易出现由于权重过度集中而导致的粒子退化现象。文献[10]提出了应用于红外图像导引头的视线角速率提取分层采样粒子滤波算法，有效解决了粒子退化现象，但是增加了系统计算负担。文献[11]提出了基于自适应预测滤波的视线角速率提取算法，利用不断变化的残差对噪声方差进行在线调整，提高了对非高斯噪声的滤波性能。由于集员滤波算法不需要已知噪声的分布特性，故在非高斯噪声环境下的视线角速率提取方面展现出良好的应用前景。集员滤波算法最初由Schweppe[12]于1968年提出。Maksarov[13]、Kurzhanski[14]和Chernousko[15]等进一步发展了针对状态和参数估计的椭球计算方法。Scholte和Campbell[16]利用区间估计方法建立了非线性系统的扩展集员滤波(Extended Set Membership Filter，ESMF)算法。文献[17]拓展了集员滤波在故障检测领域中的应用，利用次最小容积法则实现状态椭球与观测椭球的更新计算，提出了基于扩展椭球集员滤波的故障检测与隔离算法。文献[18]提出了一种基于MIT(Massachusetts Institute of Technology)规则的自适应扩展集员滤波算法，其利用MIT优化规则对状态噪声椭球进行自适应选取，实现了更快的健康度恢复速率。文献[19]提出了基于纯方位目标跟踪的外定界椭球集员估计算法，该算法采用最小化后验估计误差的李雅普诺夫函数上界的策略来获得观测更新椭球，能够更加合理地利用观测信息，并降低了运算量。

然而，以上这些考虑非高斯噪声的滤波算法均建立在状态噪声与观测噪声相互独立的前提下，没有考虑状态噪声与观测噪声的相关性对估计结果的影响。由于导弹在飞行过程中存在大量不确定的干扰因素[20-21]，例如机械振动以及弹体弹性形变等。这些客观因素使得状态噪声与观测噪声相互独立的假设难以保证[22]。为此，本文围绕考虑相关噪声解耦的视线角速率提取算法开展研究，推导了基于修正球面坐标系的视线角速率提取模型，建立了视线角速率提取模型的相关噪声解耦方法以及解耦后模型的线性化表达式，得到了相关噪声解耦的扩展椭球集员滤波算法，并以某型搭载捷联导引头的制导火箭弹为例进行了仿真验证。

1 修正球面坐标系下的视线角速率提取模型

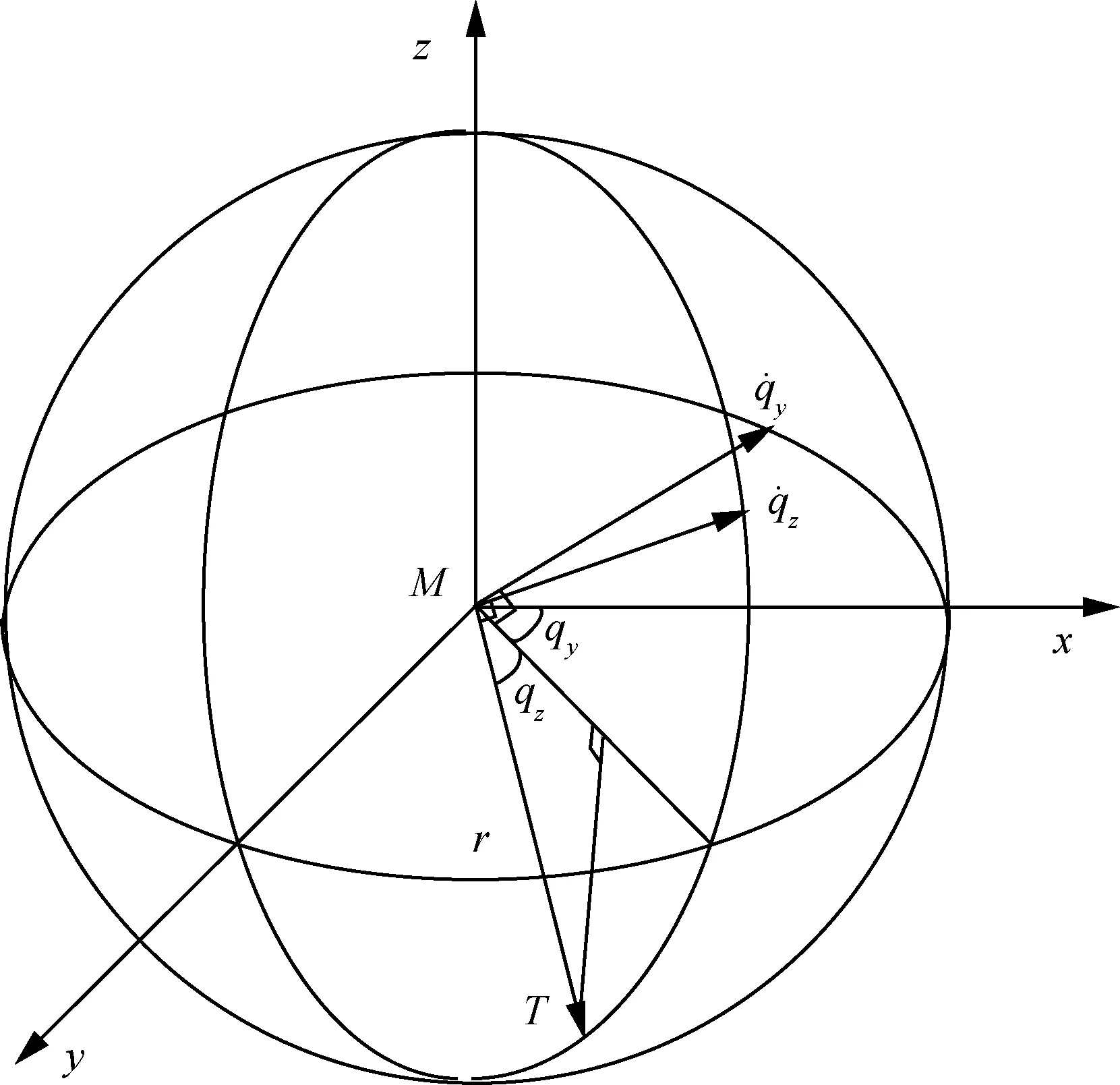
图1 弹目相对位置关系

根据球面坐标系下的弹目相对位置关系可以得到弹目相对运动方程为[2]

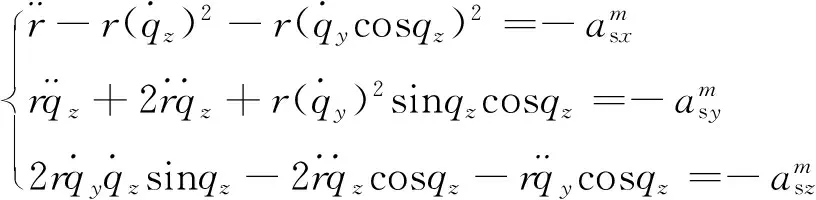
(1)

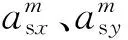
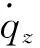
(2)

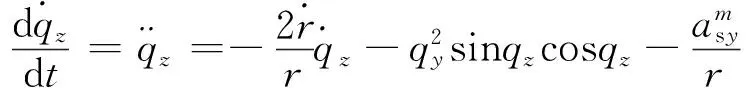
(3)

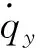
(4)

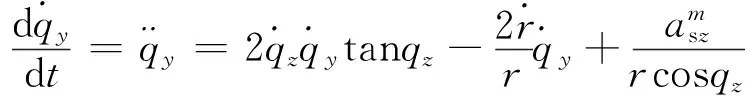
(5)

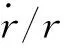
(6)

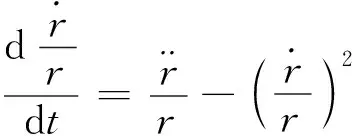
(7)

由弹目相对运动模型式(1)可知

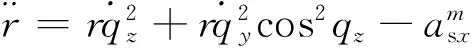
(8)

将式(8)代入式(7)并化简得到

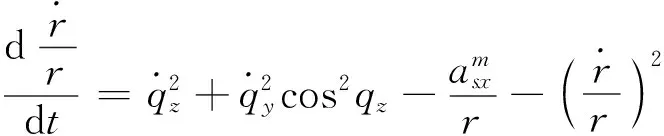
(9)

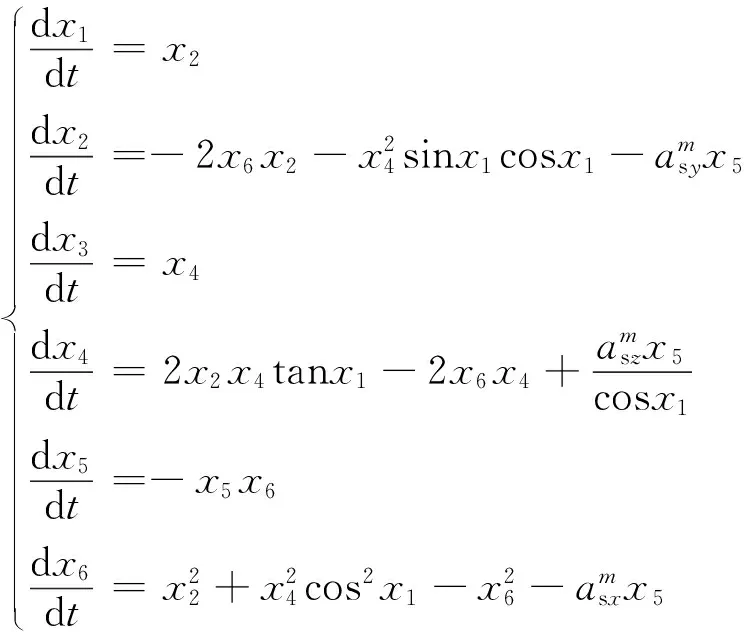
(10)

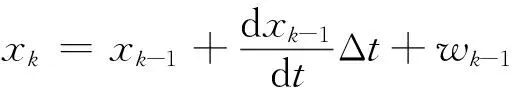
(11)

式中：Δt为采样时间间隔；wk-1为包含离散化误差的状态噪声项。

由于目标在视线坐标系和体视线坐标系中的坐标均为(r,0,0)，则经过坐标转换得到目标在弹体坐标系和地面坐标系内的投影分别为

(12)

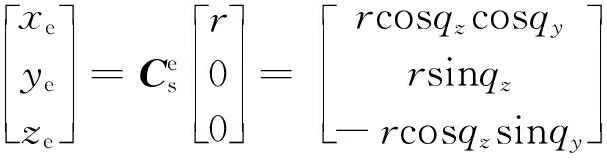
(13)

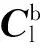
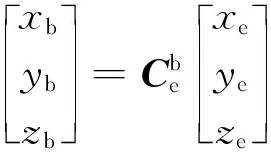
(14)

联立式(12)～式(14)并整理得到视线角解耦模型为[3]

(15)

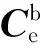
(16)

式中：γ、ϑ和ψ分别为导弹的滚转角、俯仰角和偏航角。选取捷联导引头测得的体视线高低角qα和体视线方位角qβ为观测量，可以得到观测方程为

(17)

2 考虑相关噪声解耦的扩展椭球集员滤波算法

在第1节所建立视线角速率提取模型与视线角解耦模型的基础上，针对状态与观测模型中存在非高斯相关噪声的情况，根据文献[23]中对高斯噪声假设条件下相关噪声的处理方法，利用集员滤波中椭球形状矩阵与Kalman滤波中的噪声协方差矩阵作用相似的特性，用非高斯噪声的椭球形状矩阵代替相关噪声解耦框架中的噪声协方差矩阵，对观测模型中的相关噪声进行解耦，在此基础上运用扩展椭球集员滤波算法，实现对非高斯相关噪声的滤波计算。将第1节所建立的状态模型式(10)和观测模型式(17)简写为

(18)

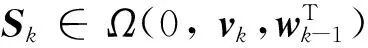
wk-1∈Ω(0,Qk-1),vk∈Ω(0,Rk)

(19)

式中：Qk-1为状态噪声椭球的形状矩阵；Rk为观测噪声椭球形状矩阵，可以将每一时刻的状态分布情况按照椭球集合定义为

Ω(a,P)={x∈Rn|(x-a)TP-1(x-a)≤1}

(20)

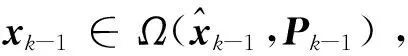
i=1,2,…，n

(21)

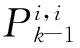
对式(18)中的观测方程做变换[22]：

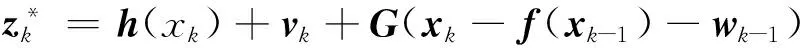
(22)

式中：G为待求矩阵，对式(22)中包含状态变量的项和噪声项分别进行合并，得到

h*(xk)=h(xk)+G(xk-f(xk-1))

(23)

(24)

则观测噪声协方差矩阵，即观测噪声椭球形状矩阵可以转换为

(25)

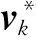
Sk-Qk-1GT=0

(26)

由式(26)得到待求矩阵G的表达式为

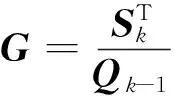
(27)

将式(27)代入式(25)得到解相关性的观测噪声椭球形状矩阵为

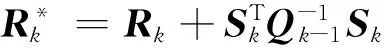
(28)

同理，将式(27)代入式(23)得到解相关性的观测函数为

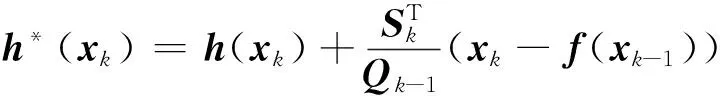
(29)

由此得到相关噪声解耦的视线角速率提取算法状态方程与观测方程为

(30)

对相关噪声解耦之后的状态模型与观测模型开展扩展椭球集员滤波算法的推导。对式(30)中的状态方程进行线性化变换，对k-1步的状态变量xk-1通过一阶泰勒级数来逼近第k步的状态变量预测值xk：

(31)

(32)

式中：Hf1,Hf2,…,Hfn为状态函数关于每个状态变量的海森矩阵(Hessian Matrix)。将状态方程的拉格朗日余项作为其误差的一部分来考虑，式(31)可以简化为

(33)

(34)

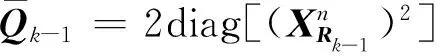
同理可以得到解相关性观测方程的线性化表达式为

(35)

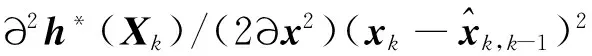
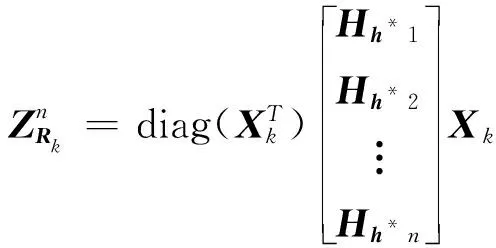
(36)

式中：Hh*1,Hh*2,…,Hh*n为解相关性观测函数关于每个状态变量的海森矩阵。同理，把解相关性观测方程的拉格朗日余项作为误差的一部分来考虑，式(35)可以简化为

(37)

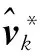
(38)

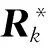
(39)

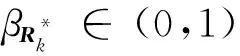
利用椭球集员滤波算法计算时间更新的状态椭球边界为

(40)

(41)

观测更新为

(42)

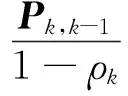
(43)

(44)

其中：

(45)

(46)

F和H分别为状态方程的系数矩阵和解相关性的观测方程系数矩阵；βk和ρk分别为时间更新椭球和观测更新椭球的调节尺度因子；δk为算法健康度因子，当状态椭球或观测噪声椭球无效时δk≥1，其表达式为

(47)

尺度因子参数的求解涉及到两个椭球直和运算得到的外包椭球最优化问题，对βQk-1、βRk和βk-1的计算选取外包椭球的最小迹计算方法，该方法求解形式简单，且与外包椭球最小化体积的优化准则相比，该方法鲁棒性更强，计算量更小。根据椭球最小迹法则有

β=argmin tr(P)

(48)

从而可以根据

(49)

获得最优的尺度因子参数，其中：P1和P2为任意两个椭球形状矩阵。

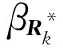
(50)

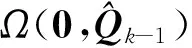
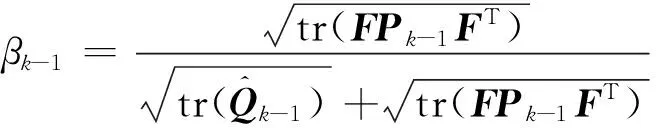
(51)

考虑观测更新的椭球形状矩阵计算公式为

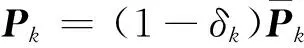
(52)

在迭代计算过程中，观测更新的椭球形状矩阵的形式往往较为复杂，导致Pk计算复杂度较高，无论采用最小化椭球体积法还是椭球最小迹法，尺度因子参数ρk的优化计算都很困难，甚至无法获得解析解。采用最小化性能指标δk的上界形式来计算，可以大大降低计算成本，根据：

ρk=argmin sup(δk)

(53)

得到尺度因子ρk的次优计算公式为

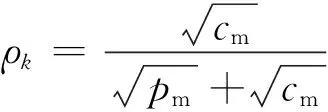
(54)

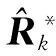
3 案例研究

本文选用装载捷联导引头的某型远程制导火箭弹的末制导仿真对算法进行验证，利用弹道仿真获得的火箭弹加速度与姿态数据实时更新状态模型与观测模型，根据比例导引律将视线角速率的提取结果实时进行导引，控制火箭弹精确命中目标。设置仿真初始时刻参数如表1 所示。

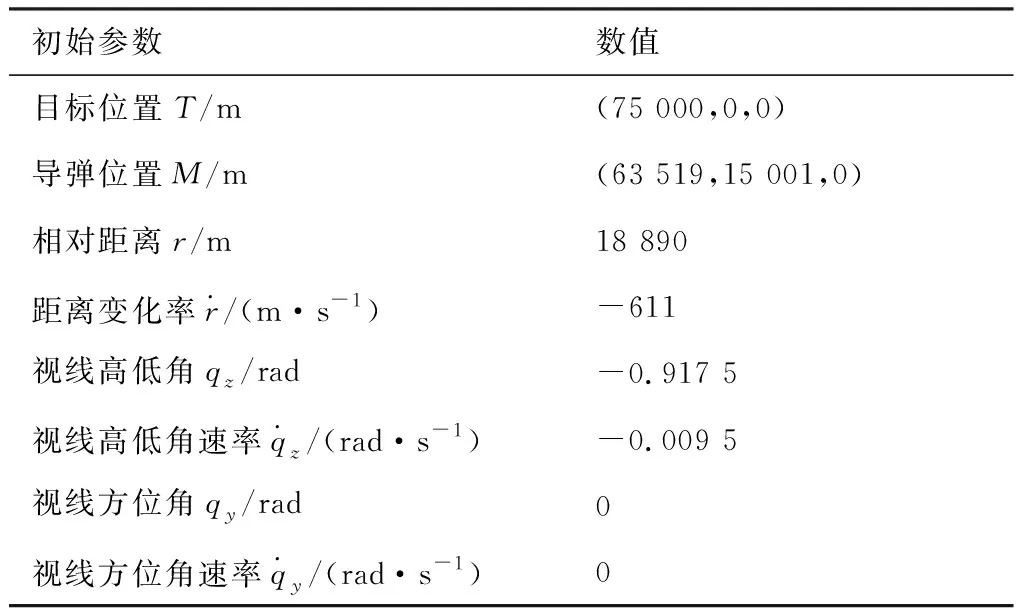
表1 初始仿真状态

选取球面坐标系下状态模型的初始值为

x0=[-0.917 5,-0.009 5,0,0,18 890,-611]T

修正球面坐标系下状态模型的初始值为

xMSC0=[-0.917 5,-0.009 5,0,0,5.293 8×

10-5,-0.032 3]T

对比两种模型初始值可以看出，修正球面坐标系模型在经过规范化处理以后，实现了状态变量从有量纲到无量纲的转换，便于后续的迭代计算。为了验证修正球面坐标系下视线角速率提取模型的性能，对修正球面坐标系下的视线角速率提取模型与传统球面坐标系下的视线角速率提取模型的估计精度进行对比分析。假设状态噪声与观测噪声均为高斯白噪声，且相互独立，其中观测噪声的均方根误差为0.035 rad。在初始条件相同的情况下，采用EKF算法分别进行仿真的结果如图2和图3所示。

图2 球面坐标系模型与修正球面坐标系模型视线高低角与视线高低角速率估计曲线

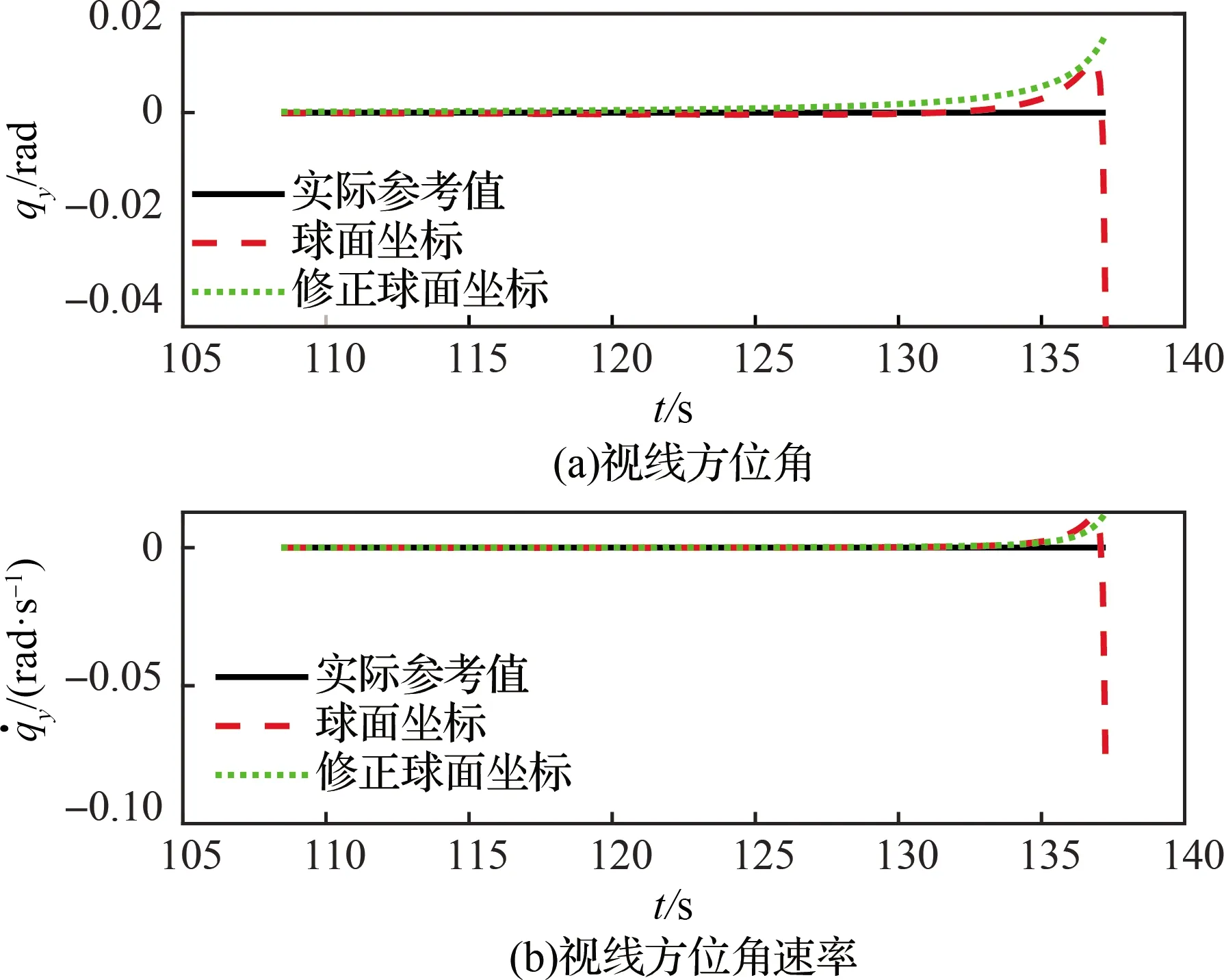
图3 球面坐标系模型与修正球面坐标系模型视线方位角与视线方位角速率估计曲线

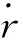
在修正球面坐标系模型的基础上，假设状态噪声与观测噪声为相互独立且满足均匀分布的非高斯噪声，其中观测噪声形状矩阵根据式(19)定义为分别采用ESMF算法和PF算法进行视线角速率提取，得到的仿真结果如图4和图5所示。

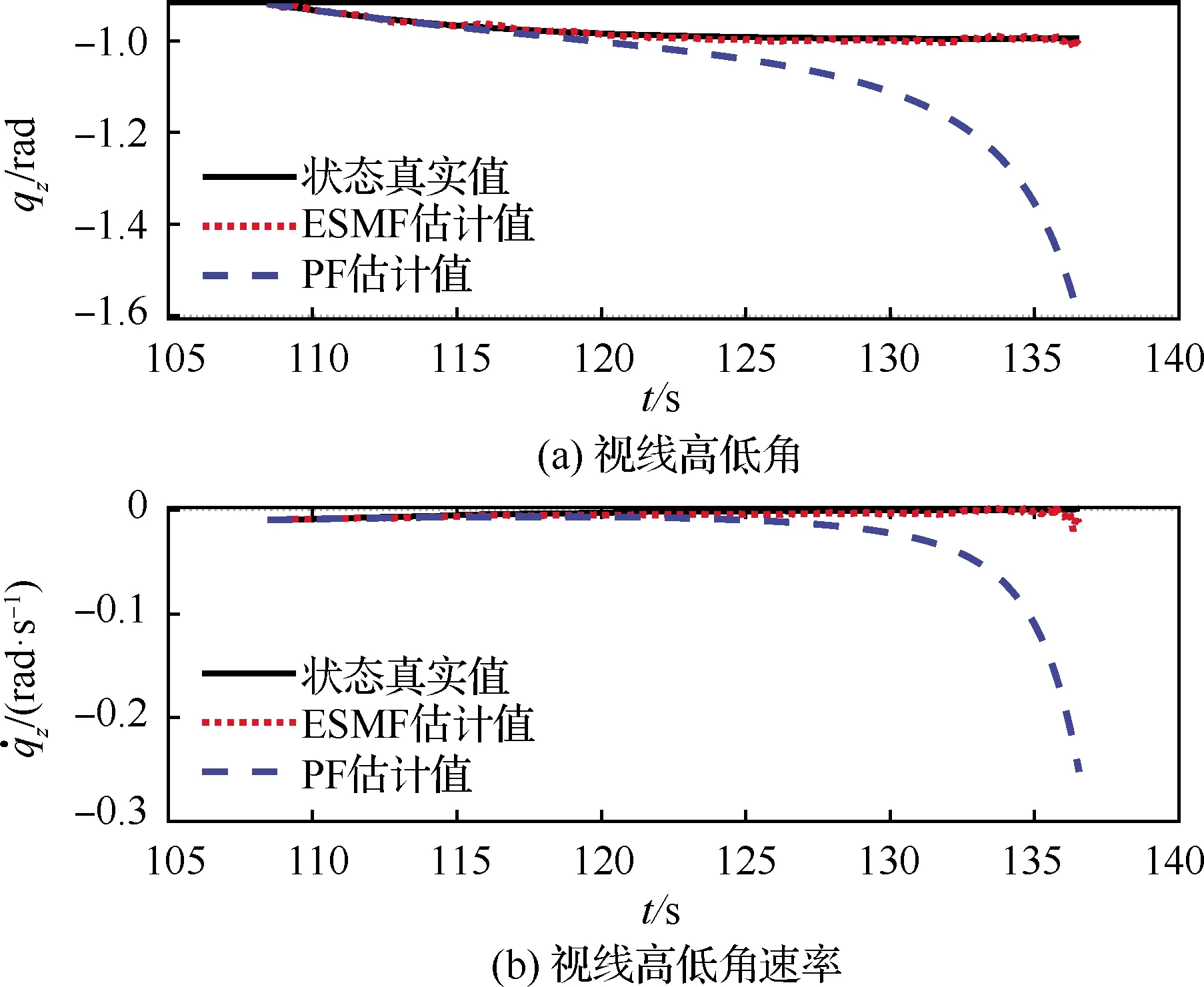
图4 ESMF与PF算法视线高低角及其角速率估计曲线

图5 ESMF与PF算法视线方位角及其角速率估计曲线

可以看出，在非高斯噪声条件下，PF算法得到的视线角及视线角速率的估计结果在后半段出现了严重发散，导致估计结果与真实状态之间的误差迅速扩大，无法提供可用的制导信息。反观ESMF算法，由于不需要已知观测噪声和状态噪声的分布情况，仅要求噪声有界，表现出更好的鲁棒性。此外，ESMF算法将线性化误差项与模型本身的噪声项通过直和计算引入到虚拟噪声椭球中，充分考虑了线性化误差对模型估计结果的影响，故该算法得到的视线角与视线角速率估计精度高于PF算法，最大误差仅为0.01 rad/s，能够满足高精度比例导引制导的需要，是一种更符合工程应用且精度较高的滤波方案。

针对噪声相关且非高斯的情况，假设状态噪声与观测噪声满足均匀分布，视线高低角与体视线高低角、视线方位角与体视线方位角存在相关性，令状态噪声与观测噪声的相关性矩阵为开展相关噪声解耦的ESMF算法仿真，与相关噪声未解耦ESMF算法的仿真结果如图6和图7所示。可以看出，未进行相关噪声解耦的ESMF算法得到的估计结果已经不能很好地跟踪状态真实值，且估计结果在末端出现不同程度的发散，其中，视线方位角速率的末段估计误差达到了0.05 rad/s以上。而采用相关噪声解耦算法得到的视线方位角速率与视线高低角速率的估计精度较高，在末段误差最大仅为0.005 rad/s，能够更好地跟踪状态真实值，实现了在非高斯相关噪声条件下对捷联导引头视线角速率的高精度估计。

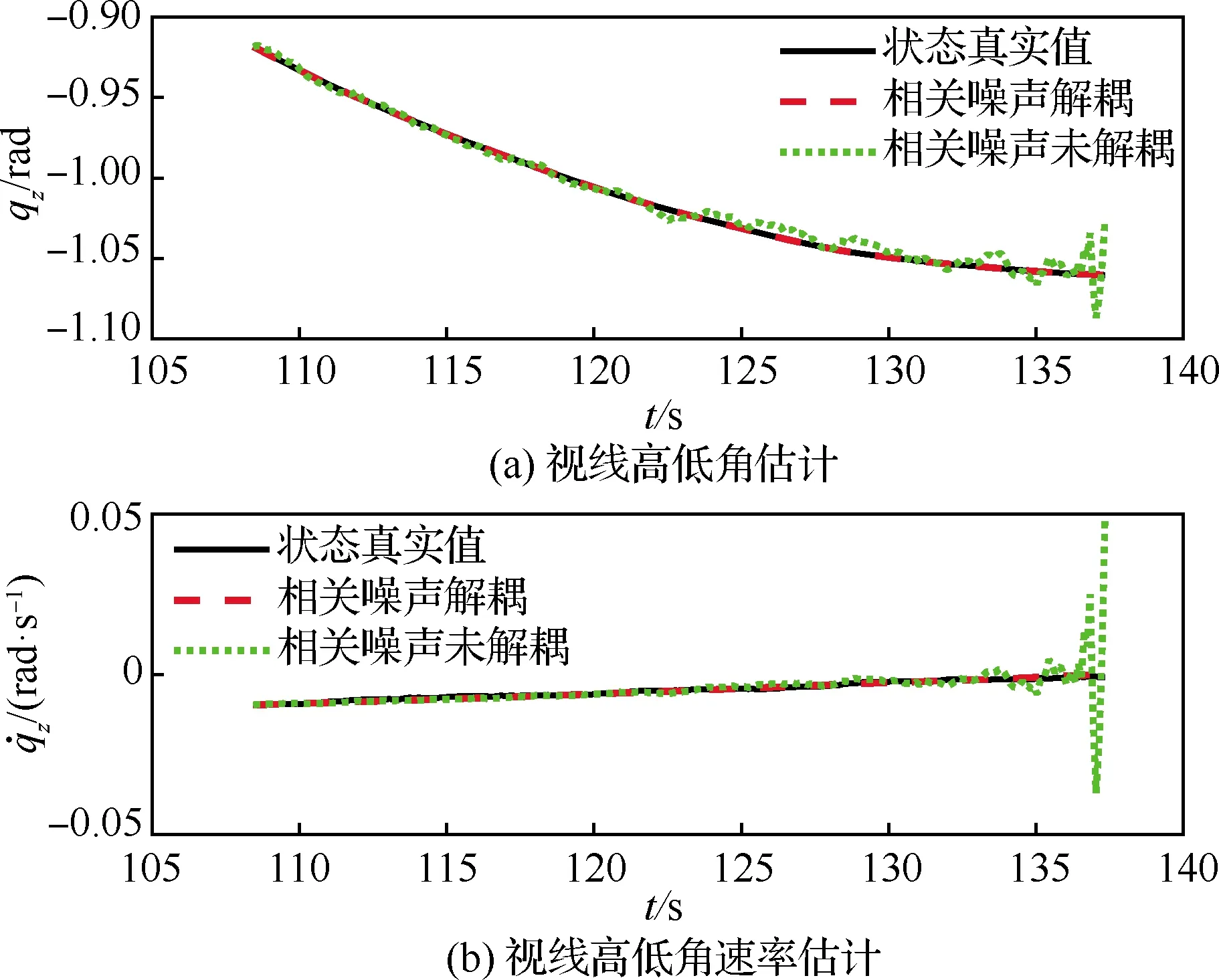
图6 相关噪声解耦与未解耦状态下视线高低角及其角速率估计曲线

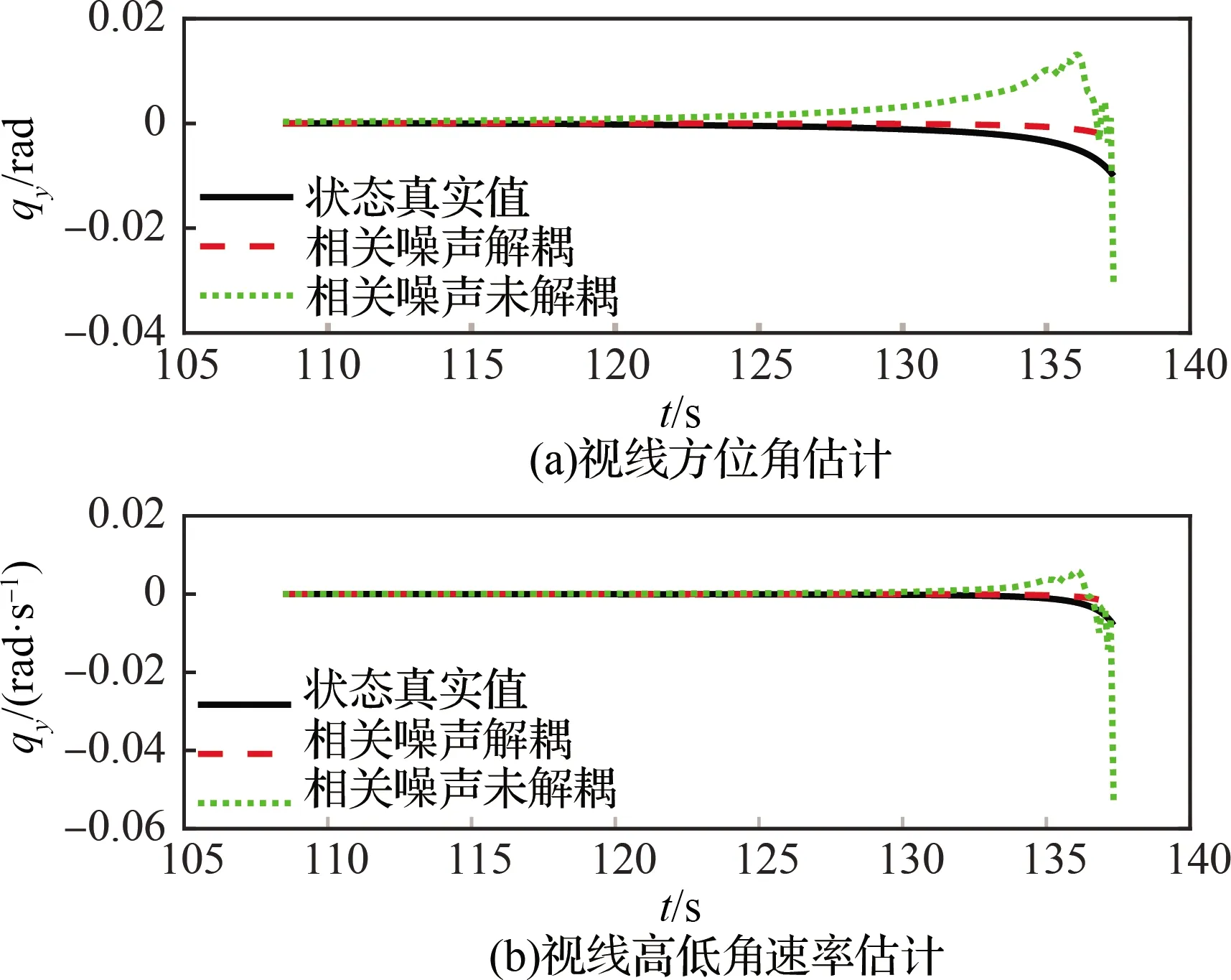
图7 相关噪声解耦与未解耦状态下视线方位角及其角速率估计曲线

4 结 论

1)通过对传统球面坐标系下的弹目距离及其变化率进行规范化处理，建立了修正球面坐标系下的视线角速率提取模型，经过仿真验证，该模型具有更高的估计精度以及更好的数值稳定性。

2)提出利用相关噪声解耦的ESMF算法解决捷联导引头的视线角速率提取问题，经过仿真验证，在模型中存在均匀噪声的条件下，其视线角速率的估计误差不大于0.005 rad/s，视线角的估计误差不大于0.01 rad，说明所提出的算法在典型非高斯相关噪声情况下具有良好的滤波精度，对于其他非高斯噪声条件下的滤波效果尚需进一步研究。