冠齿喷管射流冲击半圆形靶面的对流换热
2021-08-03吕元伟张靖周单勇孙文静
吕元伟,张靖周,单勇,孙文静
南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室,南京 210016
射流冲击广泛应用于航空发动机热端部件冷却、进口部件热气防冰和涡轮机匣间隙主动控制等多个场合[1-3]。长期以来,射流冲击对流换热强化一直是国内外研究人员关注的研究课题,大量研究业已表明,喷管形状是影响射流剪切层流动结构和靶面对流换热的一个重要因素,利用射流孔型强化冲击射流对流换热是早期研究所关注的问题[4-6],近年来,基于射流流动激励的强化换热措施得到了越来越广泛的重视[7]。其中,冠齿喷管具有阵列流向涡对的激励机制,流向涡的卷吸和强化掺混作用,改变了圆形喷管射流固有的环状剪切涡结构,增强了湍流涡团的脉动和趋近靶面射流的湍流强度[8-9],因而,冠齿射流所具有的流向涡激励不仅在连续射流[10-12]、而且在非连续射流(譬如脉冲和合成射流)[13-15]冲击换热中均被证实具有对流换热强化的作用机制。
在实际应用中,射流冲击靶面常常是带有曲率的表面,Cornaro等[16]采用烟线显现测试方法对单孔圆形自由射流冲击凹、凸半圆柱形靶面的流场进行了研究,并与平直靶面进行了对比分析,指出冲击靶面的曲率影响了射流剪切涡和边界层流动结构的稳定性。众多研究人员针对圆形喷管射流冲击凹、凸靶面对流换热开展了大量的研究[17-20],研究结果表明,靶面曲率效应对于射流冲击对流换热的影响具有高度的多参数关联影响机制。Zhou等[21]实验研究了笛形管单孔射流冲击凹靶面的对流换热,指出相对表面曲率(定义为Cr=d/D,其中,d为喷管直径,D为曲面直径)对于对流换热的影响与其变化方式有关,当靶面直径固定时,随相对表面曲率的增加,射流驻点和平均对流换热系数得到提高;相反,当喷孔直径固定时,相对表面曲率的增加则引起对流换热的降低。Guan等[22-23]结合发动机进气整流锥的热气防冰结构,通过数值和实验研究对比分析了圆形喷管和冠齿喷管热射流冲击锥形凹壁的壁面加热效果,研究表明,冠齿喷管热射流冲击具有更高的加热效率。作者团队[24]实验研究了单排冠齿射流冲击不同曲率凹形靶面的对流换热,并与圆形喷管射流进行了对比。
相对而言,对于冠齿喷管在曲靶面上的射流冲击强化传热研究还比较缺乏,为阐明不同曲率靶面上冠齿射流相对于圆形射流的换热强化作用,本文针对凹形和凸形半圆柱靶面,在典型的射流雷诺数和冲击间距下开展单股冠齿射流和圆形射流的冲击对流换热实验研究,并结合流场的大涡模拟分析,揭示不同靶面上冠齿射流强化传热的作用机制差异。
1 实验过程
1.1 实验系统
实验系统如图1(a)所示,压缩空气经过调节阀和流量控制器进入射流管,射流管直径(d)为 10 mm、长径比(l/d)为12。图1(b)所示为半圆形凹靶板实验模型,直径为D=10d,纵向长度为L=15d。冲击靶板由支撑框架和加热膜片组成,支撑框架为厚度5 mm的镂空耐热板(导热系数为0.05 W/(m2·K)),厚度为0.05 mm的铜镍铬合金加热膜黏附在半圆形支撑框架上,两端由铜棒压紧,热膜加热的电流由直流稳压电源提供。为了减少加热膜向环境的散热损失,在靶面背侧加装隔热箱,正对加热膜一侧的隔热壁上开设红外测试窗口,安装红外透过率约为0.97的红外玻璃,加热表面温度由红外热像仪测量。半圆形凸靶板实验模型结构参数与半圆形凹靶板一致。

图1 射流冲击实验系统示意图
6-锯齿冠齿喷管结构如图2(a)所示,6个锯齿在周向均匀布置,锯齿为平直弧齿,即锯齿中线与喷管轴线平行,锯齿高度(a)为6 mm,锯齿根部对应的弧长(W)为πd/6。锯齿与靶面的相对关系如图2(b)所示,半圆形靶面纵向x轴上坐落锯齿齿尖的投影点,沿曲面方向s轴上坐落锯齿齿谷的投影点。依据已有的研究[11-15],射流冲击间距(H)定义为锯齿根部至冲击靶面的距离,冲击靶板固定于位移机构上,通过该位移机构调节射流冲击间距比(H/d)。冲击靶面温度分布由红外热像仪测量,测试方法详见文献[12]。
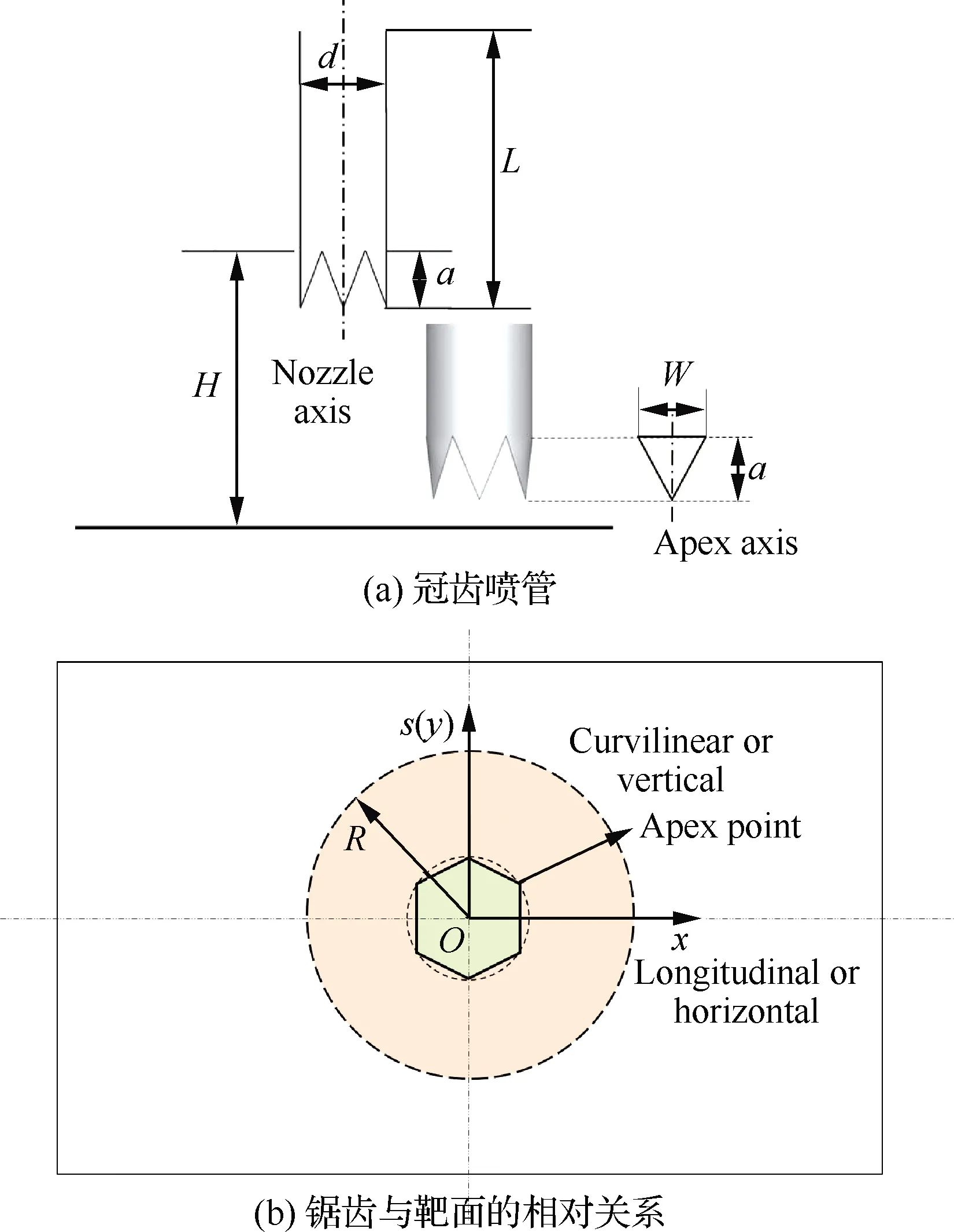
图2 冠齿喷管结构示意图
1.2 数据处理和不确定度分析
实验过程中,电加热输入热流密度(qjoule)由施加于加热膜的电压(V)和电流(I)以及加热膜面积(A)确定,恒定为4 500 W/m2,记加热膜背侧表面(相对于射流冲击侧)向环境的散热热流密度为qs,射流冲击的局部对流换热系数确定为
(1)
式中:Tj为冲击射流温度,由喷管出口处的温度探针测得;Tw为冲击靶面温度,采用工作波段为8~14 μm的红外热像仪测试。
加热膜背侧散热热流密度由隔热箱外表面的热电偶测试温度并按照经验关联式预估[25]:
(2)
式中:Ta和Tb分别为环境温度和隔热箱外表面平均温度;heff为等效换热系数。由此预估的散热损失约占加热输入热流的5%。
射流冲击局部努塞尔数Nu定义为
(3)
式中:k为射流的导热系数。
局部努塞尔数的测试不确定度按照误差传递理论分析[26],即
Nu=f(x1,x2,…,xn)
(4)
(5)
式中:f为独立变量(x1,x2, …,xn)的函数;Δ(xi)为对应变量xi的标准不确定度。根据式(1)和式(3)选择qjoule、qs、Tw、Tj、k和d这6个独立变量,其误差来源及最大不确定度如表1所示。按照式(5),局部努塞尔数的测试不确定度约为±7.3%。

表1 独立测试量的不确定度
2 实验结果与分析
2.1 局部努塞尔数分布特征
图3为Re=8 000下,单股圆形射流冲击半圆形靶面在不同冲击间距下的局部努塞尔数分布。可以看出,在H/d=1时,圆形射流冲击在半圆形靶面上依然存在局部努塞尔数分布的“双峰”现象。其内环对应于射流冲击驻点,这是趋近壁面射流直接撞击的强局部对流换热区;外环出现在距射流驻点约1.5d的位置处,这是由于射流冲击壁面形成强烈偏转,沿射流驻点径向向外壁面射流区的强剪切所致。相比之下,“双峰”现象在凸靶面上更为清晰,同时,在凸靶面上射流驻点附近的局部对流换热要高于凹靶面。
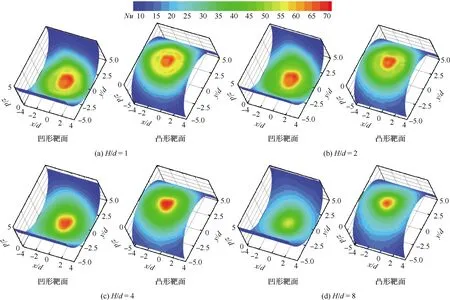
图3 圆射流冲击局部努塞尔数分布(Re=8 000)
图4为Re=8 000下,单股冠齿射流冲击半圆形靶面的局部努塞尔数分布。可见看出,在H/d=1时,冠齿射流冲击局部努塞尔数分布呈现明显的瓣状分布特征,但内环的波瓣顶角与外环的波瓣顶角在周向上呈交错,在内环瓣状分布中,高的局部换热区域对应于冠齿的齿谷位置。已有研究表明管内气流自冠齿尾缘喷管出口喷射时受到锯齿的流动激励作用,在齿尖处生成流向涡对[8-9],该流向涡对能够在相邻锯齿之间的齿谷形成融合,因而在对应于齿谷的靶面上形成局部对流换热强化;自驻点向外,随着射流贴壁向外流动,对应齿尖的径向有更高的聚流效应,外环中高局部对流换热系数对应的波瓣顶角发生周向偏移而与锯齿齿尖相一致。冠齿射流冲击局部努塞尔数瓣状分布特征在H/d=2时也依稀可见,对比2种不同形式的半圆形靶面,局部努塞尔数分布的瓣状分布特征在凸形靶面上更为明显。当射流冲击间距比达到4后,冠齿射流冲击在驻点附近周向上的局部对流换热差异已趋于消失,整体呈现出常规圆射流冲击的特征。
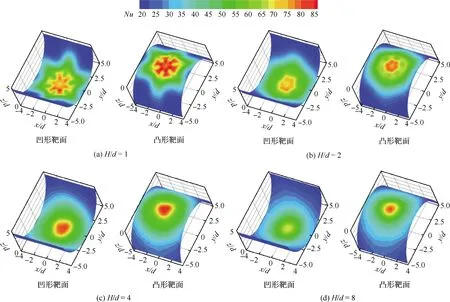
图4 冠齿射流冲击局部努塞尔数分布(Re=8 000)
2.2 平均努塞尔数对比
针对图2(b)所示,在展开的二维平面上沿射流冲击驻点径向位置进行对流换热系数的周向平均,图5和图6分别为凹形和凸形靶面上,圆形射流冲击和冠齿射流冲击换热周向平均努塞尔数(Nuav,R)沿驻点径向分布的对比,在不同的射流雷诺数和射流冲击间距下的对比,其中R为曲面展开为平面后,与滞止中心的距离。

图5 凹形靶面圆形射流和冠齿射流冲击周向平均努塞尔数分布
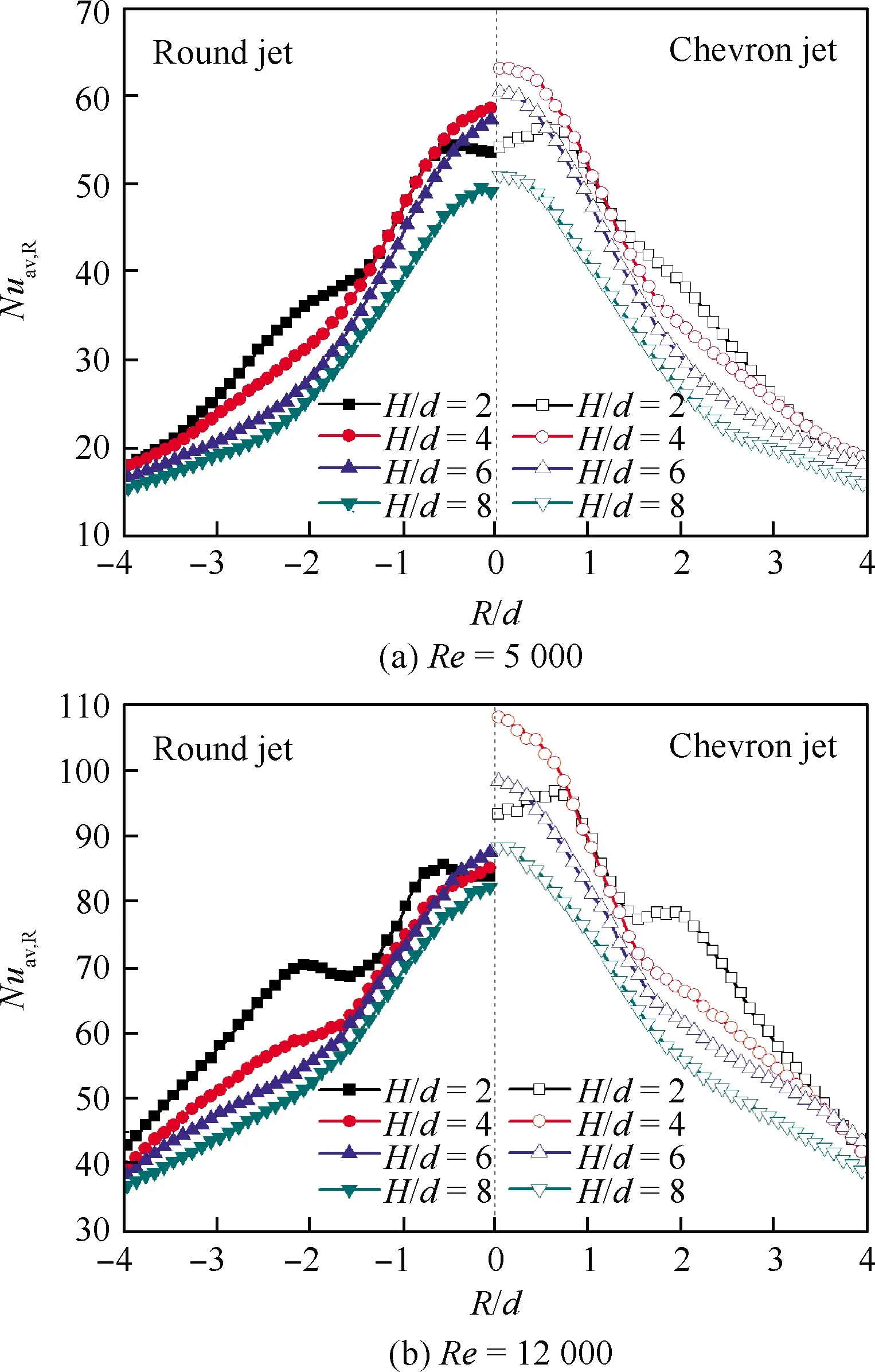
图6 凸形靶面圆形射流和冠齿射流冲击周向平均努塞尔数分布
无论是在凹形靶面还是凸形靶面上,不同射流雷诺数和射流冲击间距下,冠齿射流冲击均呈现出相对于圆形射流的传热强化效果,对比2种不同形式的靶面,冠齿射流冲击的传热强化效果依然存在一定的差异。对于凹形靶面,冠齿射流相对于圆形射流在驻点的对流换热增强在10%以内,在邻近射流驻点的壁面射流区,冠齿射流冲击相对于圆形射流体现出较为显著的对流换热改善;对于凸形靶面,在较高的射流雷诺数下,冠齿射流在H/d=4时的驻点对流换热增强相对于圆形射流可以达到20%左右。
图7显示了Re=8 000时冠齿射流冲击2种曲率靶面的面积平均努塞尔数(Nuav,A)对比。可以看出,在本文所研究的射流冲击间距比下,凸形靶面的对流换热系数均高于凹形靶面。除H/d=2之外的几个射流冲击间距下,射流驻点附近1倍射流孔直径区域内的冠齿射流冲击凸形靶面换热面积平均努塞尔数Nuav,A较凹形靶面的相对提高幅度在15%左右,表明在较大的射流冲击间距下,靶面对冠齿射流冲击换热的影响更为显著。
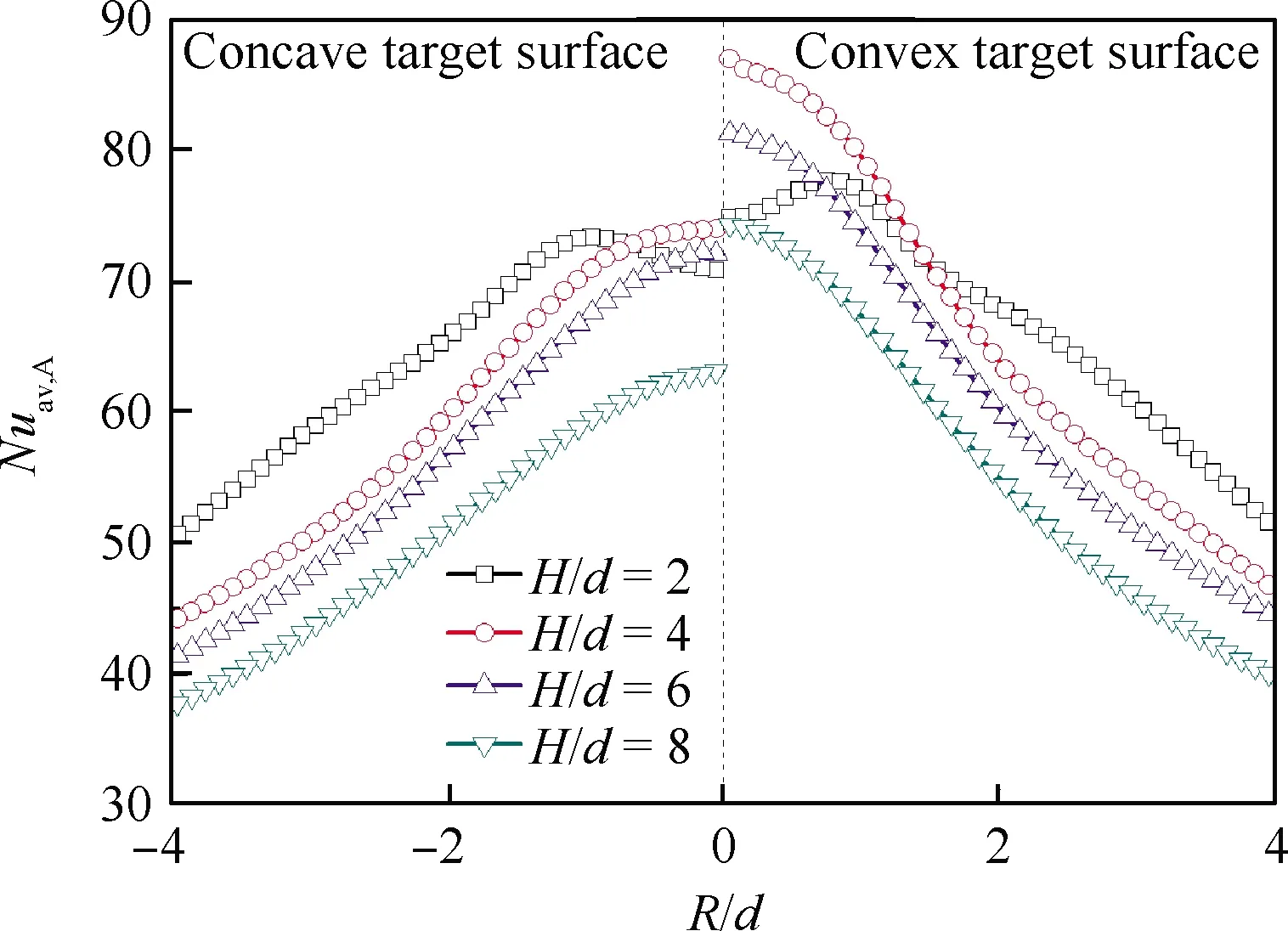
图7 不同靶面的面积平均努塞尔数对比(Re=8 000)
3 流场大涡模拟
3.1 计算过程
为揭示不同靶面冠齿射流冲击换热的流场特征,运用CFD软件进行了大涡模拟分析,选用基于涡黏性假设的Smagorinsky-Lilly经典亚网格模型[27]。按照实验模型所建立的冠齿射流冲击凹形靶面和凸形靶面计算域如图8所示。相应的边界条件设置如下:喷管进口边界条件设为速度进口,鉴于射流管出口射流具有充分发展湍流的速度剖面[16],本文依据圆管充分发展湍流流动的1/7幂次方定律分布近似设置进口速度分布,对应的射流雷诺数Re=8 000,射流温度Tj=300 K,冲击靶面采用无滑移速度边界条件,热边界为恒热流边界,恒定为4 500 W/m2;计算域外场空间在展向选取为2.5倍半圆形靶面直径,边界设置为压力出口,即环境压力。
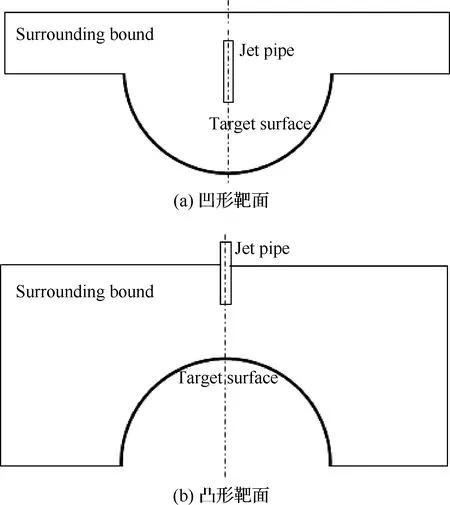
图8 计算域示意图
计算网格划分采用结构化和非结构化混合方式,冠齿喷口附近区域使用非结构化网格,其中冠齿喷管表面进行局部加密,网格单元最小尺度为0.05 mm;靶面近壁区利用附面层网格进行加密,多次尝试后得到,贴近靶面处设置20层附面层网格,第1层高度0.02 mm,增长因子为1.2,保证无因次法向距离z+<1,以满足大涡模拟计算要求。凹形靶面局部网格划分如图9所示,网格总数达到2 500万左右。
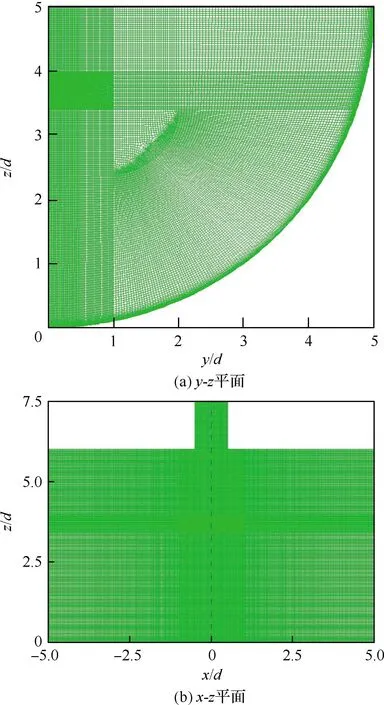
图9 凹形靶面局部网格
数值模拟采用非稳态隐式求解器,各参数的离散均采用二阶精度的迎风格式,解收敛的各项残差小于1×10-5,时间步为1×10-4s,每个时间步迭代次数为100次。
图10给出了Re=8 000时冠齿形射流冲击凹形靶面局部努塞尔数分布的数值模拟结果,图11给出了Re=8 000、H/d=4工况下,冠齿射流冲击凹形靶面和凸形靶面表面周向平均努塞尔数Nuav,R分布的数值模拟与实验结果的比较,可以看出,本文的计算结果在射流驻点附近有一定的过预测,在凹形靶面和凸形靶面下,数值模拟的射流驻点努塞尔数与实验值的最大相对偏差分别约为9%和7%。在冠齿射流冲击不同形状靶面以及不同射流冲击间距下的对流换热变化趋势上,数值预测与实验结果均是相符的。
3.2 计算结果分析
图12为Re=8 000的圆形射流和冠齿射流在H/d=4时冲击凹形和凸形靶面,用速度染色的、基于Q-准则[28]涡识别的瞬时流场大涡模拟结果。对于圆形射流,自喷口喷出后沿下游的发展过程中,与周围空气剪切和卷吸生成轴对称的环形涡,冲击至靶面后在靶面射流驻点区附近形成强的剪切,呈现出环绕射流驻点的、近乎完整的环状形涡核,在偏离射流驻点的径向壁面射流区,壁面射流使得靶板表面形成离散的发卡涡相干结构,这些相干结构在随着壁面射流向下游运动的过程中逐渐抬升、破碎和消失。对于冠齿射流,自喷口喷出后沿下游的发展过程中,由锯齿尾缘剪切诱导出的流向涡,改变了圆形射流轴对称的环形涡内在特征,形成条纹状的涡核相干结构,在射流驻点外围的聚合和作用区域较圆形射流有明显的增强。相对于凹形靶面,冠齿射流对凸形靶面射流驻点附近的涡结构改变更为显著,靶板表面条纹状涡核结构在向下游运动的过程中与壁面的贴合明显强于凹形靶面,而在凹形靶面上,射流冲击在驻点外围的环状涡结构更为稳定。这证实了冠齿射流对凹形靶面射流涡结构的影响机制要弱于凸形靶面,在对流换热特性上体现为冠齿射流冲击局部努塞尔数的瓣状分布特征在凹靶面上有所弱化,如图4(a)和图4(b)所示。

图12 速度染色的Q-准则涡识别(Q=500 000)
图13对比了H/d=4时,冠齿射流冲击2种不同形状靶面的脉动均方根(RMS)速度分布云图,图14对比了时均温度分布云图,图中均叠加了时间平均的流线分布。可以直观地看出,冲击靶面的形状影响了射流剪切和壁面射流边界层流动结构,对于凹形靶面,由于腔内形成大尺度的回流流动,冲击射流的发展将受到凹腔中的回流结构影响而发生卷吸和掺混。图15呈现了s/d=2位置处,壁面射流区的时均速度(Umean)和RMS速度(URMS)在靶面法线方向的分布,其中,U为喷嘴出口的时均速度,无论是凹形还是凸形靶面,冠齿喷嘴的壁面射流区流体的时均速度和RMS速度峰值均大于圆形喷嘴的且更紧贴靶板表面,表明冠齿喷嘴形成更强的壁面剪切作用,对应地诱导出更强的对流换热;也可以看出,凸形靶面下的壁面射流时均速度和RMS速度峰值也高于凹形靶面。同时,也应注意到,凹形靶面构成的自然受限空间所诱导的回流结构除了直接影响冲击射流的剪切发展之外,还会影响冲击靶面附近的温度场,在回流结构的作用下,较高温度的壁面气流被卷吸侵入至凹腔底部。从而导致冠齿射流冲击凹形靶面的对流换热能力弱于相同冲击参数下的凸形靶面,这个规律为对流换热的实验结果所证实。
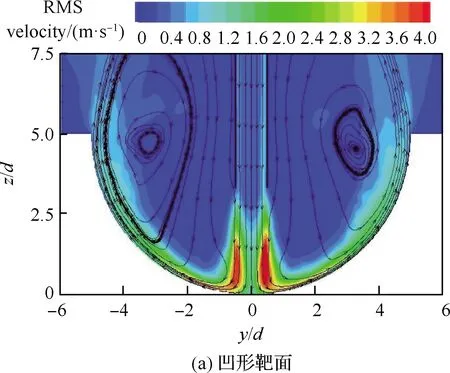
图13 y-z截面上的冠齿射流脉动均方根速度云图
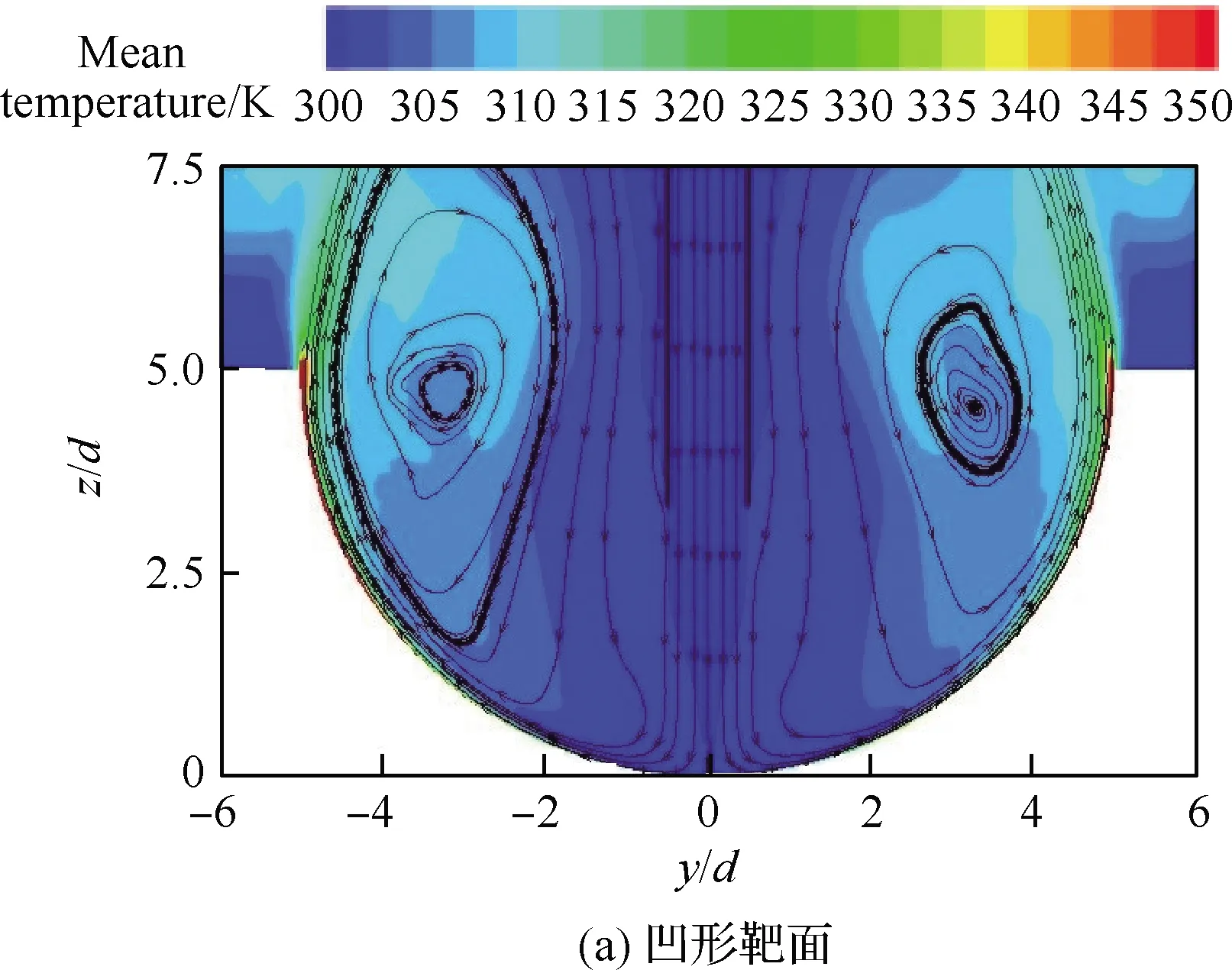
图14 y-z截面上的冠齿射流冲击时均温度云图
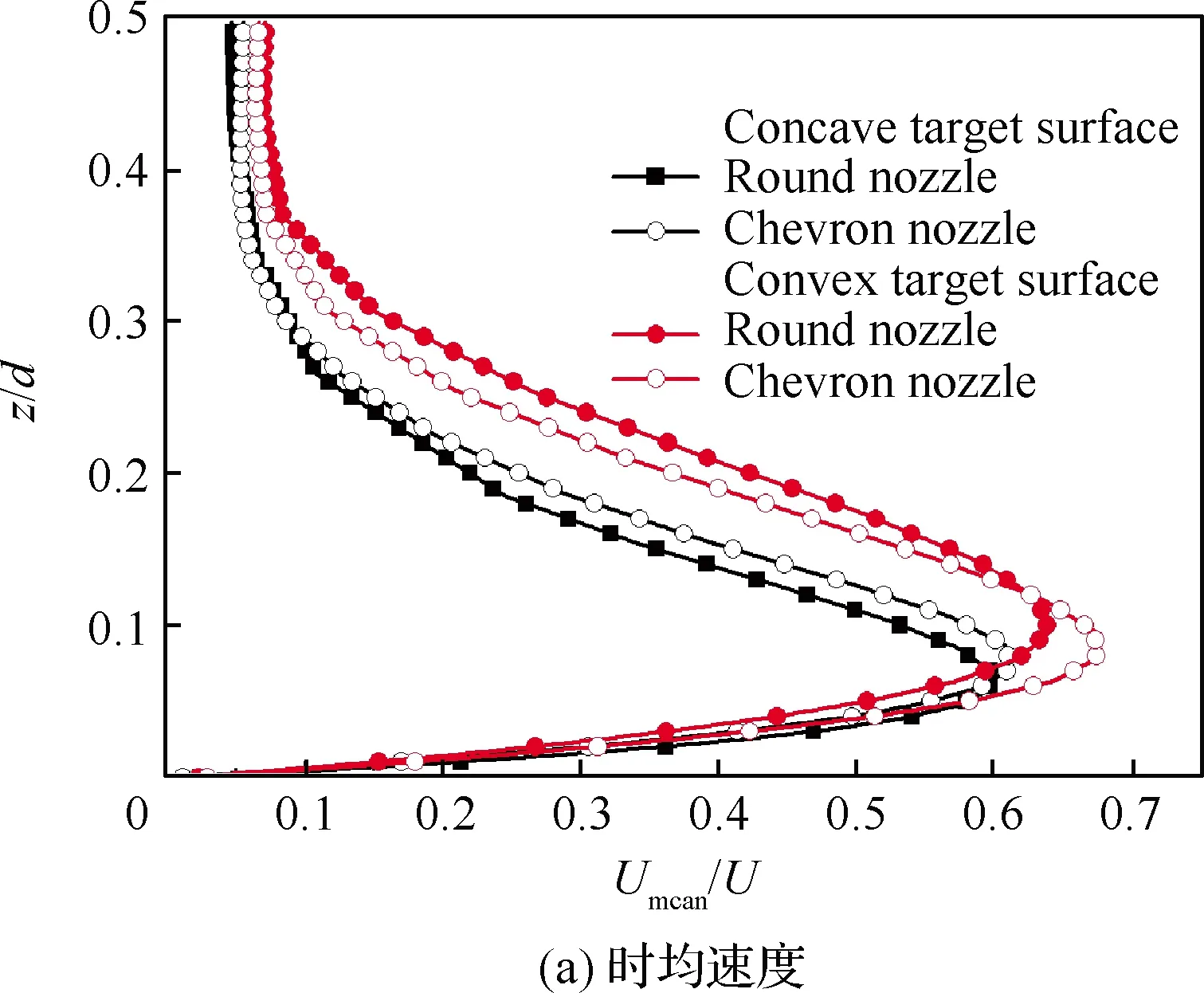
图15 s/d=2位置处壁面射流时均速度和脉动均方根速度
为了进一步分析不同射流冲击间距下凹腔内部回流的影响,以Re=5 000的冠齿射流冲击为例,图16和图17分别显示了不同射流冲击间距下,冠齿射流冲击凹形靶面的时均速度和脉动均方根速度分布云图。在小射流冲击间距下(H/d=2),如图16(a)和图17(a)所示,凹腔中的回流结构基本未形成,壁面射流能够顺畅地沿靶面曲率方向流出,因此,与凸形靶面相比,凹腔中回流结构对于射流冲击发展的影响较小,主要体现在壁面曲率对于壁面射流的影响,从对流换热实验结果中可以看出,2种靶面在射流驻点附近的差异不大;当H/d=4时,如图16(b)和图17(b)所示,凹腔中出现一个大尺度的回流区,该回流区出现在冲击射流的上游;随着射流冲击间距的增加,如图16(c)和图17(c)所示,该回流区出现在邻近射流喷口下游,对射流的发展造成更加显著的影响。同时,也可以看出,随着射流冲击间距的增加,趋近靶面的射流速度呈现衰减趋势,然而射流脉动均方根速度及其影响范围却在增加,因此对流换热较优的射流冲击间距应该使上述2个因素达成协同,H/d=4时的射流趋近靶面速度和脉动均方根速度均较高,是一个较优的射流冲击间距。
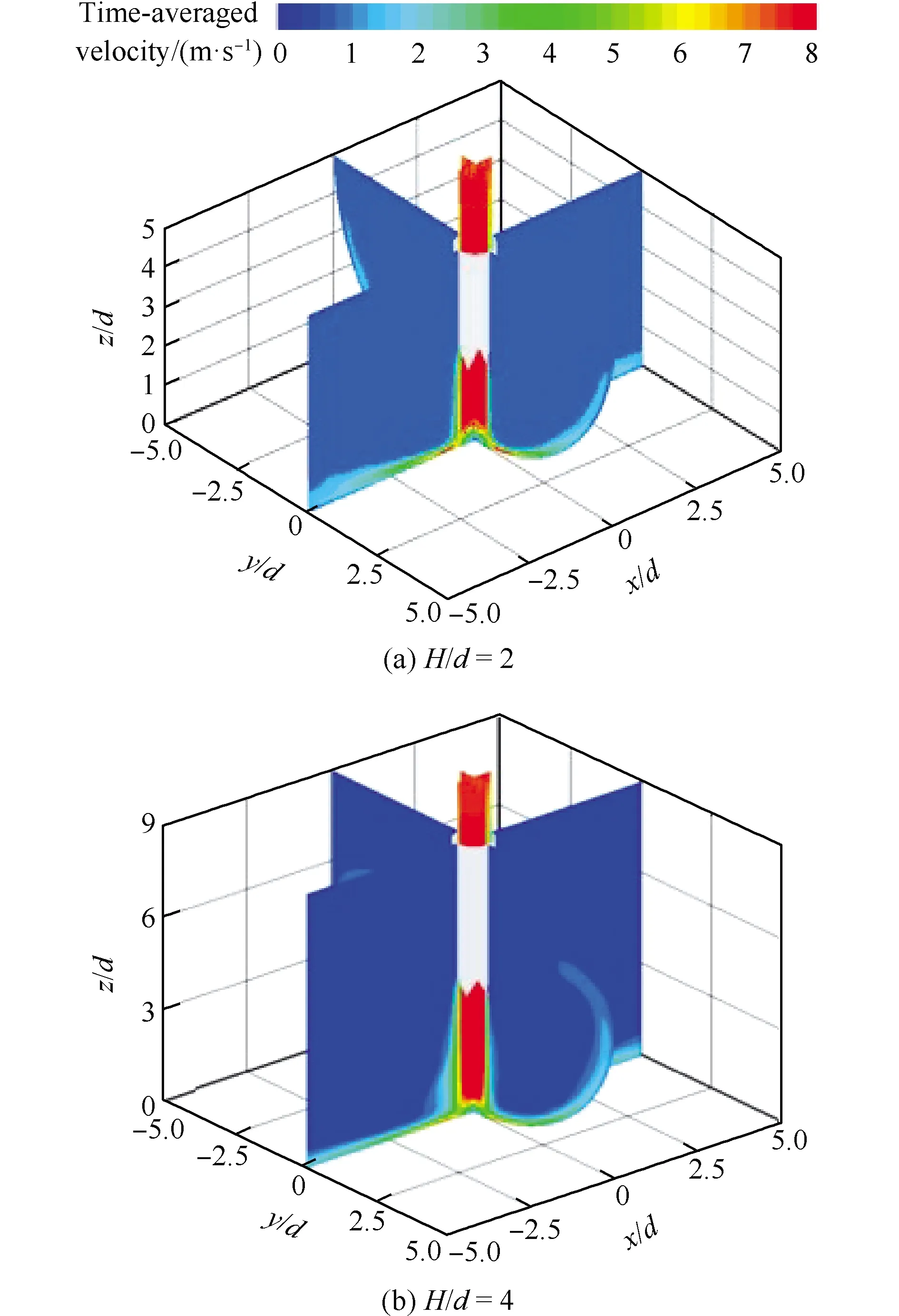
图16 冠齿射流冲击凹形靶面时均速度云图

图17 冠齿射流冲击凹形靶面脉动均方根速度云图
4 结 论
针对d/D=0.1的半圆柱凹形和凸形靶面,在典型的射流雷诺数和冲击间距下开展了单股冠齿射流和圆射流的冲击对流换热实验研究,并进行了流场的大涡模拟分析,主要结论如下:
1)在H/d=1时,圆射流冲击半圆形靶面上存在局部努塞尔数分布的双峰现象,冠齿射流冲击局部努塞尔数分布则呈现明显的瓣状分布特征。相比之下,无论是圆形射流冲击的双峰分布现象还是冠齿射流冲击的瓣状分布,在凸靶面上更为清晰。
2)冠齿射流改变了圆形射流轴对称的环形涡内在特征,形成条纹状的涡核相干结构;对比2种不同形式的靶面,冠齿射流冲击的传热强化效果存在一定的差异,其强化作用机制在凸靶面上更为显著,在较高的射流雷诺数下,冠齿射流在H/d=4时的驻点对流换热增强相对于圆形射流可以达到20%左右。
3)冲击靶面形状影响射流剪切和壁面射流边界层流动结构,导致冠齿射流冲击凹形靶面的对流换热能力弱于相同冲击参数下的凸形靶面,尤其是在较大的射流冲击间距下,射流驻点附近1倍射流孔直径区域内的冠齿射流冲击凸形靶面换热面积平均努塞尔数Nuav,A较凹形靶面的相对提高幅度在15%左右。
本文仅针对特定曲率的半圆柱靶面进行了冠齿射流冲击对流换热研究,鉴于靶面曲率效应的复杂性,仍然需要开展更深入的研究。
