求最短距离，育核心素养

田淑琴

【摘要】教材的例题习题的教育价值不仅仅在于巩固知识，更在于思想的渗透、文化的感染。习题中“将军饮马”题型的教学，应从培养学生素养出发，进行思想方法的渗透、解题技能的传授。

【关键词】数学核心素养;“将军饮马”题型;解题教学

在提倡核心素养的教育背景下，数学素养是指满足学生终身发展和社会发展所必备的数学方面的必备品格和关键能力，是现代社会每一个公民应该具备的基本素养。因此，核心素养视角下的数学教学理念不仅要关注知识本身，还要关注知识的文化背景和学生的应用迁移能力。下面以教材中一道习题为例，在解题教学中如何培养与渗透数学核心素养，谈谈笔者的实践与思考。

一、原题呈现

题目选自北师大版七年级下册第五章《生活中的轴对称》第三节《简单的轴对称图形》第一课时的习题5.3第5题。原题如下：

如图1所示，要在街道旁修建一个奶站，向居民区A，B提供牛奶，奶站应建在什么地方，才能使A，B到它的距离之和最短？

二、教学价值

本习题属于著名的“将军饮马”题型，是一道经典的几何最值问题，语出唐朝诗人李颀的《古从军行》：“百日登山望，黄昏饮马傍交河。”这个问题在西方也有传说，早在古罗马时代，亚历山大城有一位精通数学和物理的学者，名叫海伦。有一天，一位将军专程拜访海伦，求解这个让他百思不得其解的问题，当时，海伦稍加思索便圆满地解答了这个问题。“将军饮马”题型不仅显示着古人的数学智慧，而且充分彰显着数学灿烂的文化价值和不朽的应用价值。

一方面，学生在学习了“作一个点关于某条直线的对称点”“线段公理”“轴对称性质”等数学理论的基础上练习此题，旨在巩固和联系已学知识，发散学生思维。这类题型具有科学性、典型性、示范性和功能性，对学生的综合要求高。

另一方面，最短距离问题一直是各省地市中考数学的热点问题，往往会以圆、菱形、正方形等具有轴对称性的几何图形、二次函数等为载体出现，练习此题有助于学生获得必要的技能，从而为后续学习和解决问题奠定基础、提供支持。因此，掌握此题的解题技巧尤为重要。

三、功能分析

基于《义务教育数学课程标准（2011年版）》（以下简称《课程标准》）中提倡的“四基”教学，笔者对本道习题的功能作以下层面的分析：

从知识层面上看，巩固“作一个点关于某条直线的对称点”“两点之间，线段最短”“轴对称性质”等知识点。

从技能层面上看，发展学生的尺规作图能力、抽象思维能力、分析问题和解决问题的能力。

从思想方法上看，在解题过程中让学生经历从现实问题抽象成数学问题的过程，体会转化思想（求位于直线同侧两点到直线的最短距离之和转化为求位于直线异侧两点的最短距离之和）、类比思想（作A/B的对称点类比作B/A的对称点）。

从活动经验上看，学生通过数学学习活动，演绎、归纳“位于直线同侧两点到直线的最短距离之和”的思想方法，培养勇于质疑、敢于创新的精神，积累数学探究、发现知识的經验，激发学生热爱数学文化的情感，感受数学的文化价值和应用价值。

同时，在教学过程中体现以上功能的有机整合。

四、教学方法

根据“让学生从生活走进数学、发挥学生的主体地位”这一课程基本理念，笔者尝试从学生的情况出发：到七年级下学期，学生已经具有初步的观察和逻辑推理能力，活泼好动的他们更希望独立思考和发表见解。

鉴于此，笔者确定的教法是启发引导法，同时在教学中采用多媒体、几何画板和板书相结合的教学手段，变抽象为形象，有效地调动学生学习的积极性，有力地突破解题的难点。此外，笔者认为应引导学生采用自主探索、讨论学习、类比学习的学习方法，具体为教师设问，学生思考，然后师生互动交流，共同探索和解决题目。与此同时，在教学中，注意反馈调控，观察学生的活动参与度。

五、教学实施

1.独立思考，动手画图

师：数学史上的“将军饮马”题型，也就是“求最短距离问题”，可追溯到我国唐朝期间，甚至是西方古罗马时代，当时亚历山大城的学者海伦稍加思索便解答了这个问题。通过前面的学习，我们尝试独自用尺规作图的方法画出奶站的位置。（学生自主探索，动手画图，教师巡视。5分钟后，笔者发现学生的错误做法主要有以下三种，其中图4的做法占比重较大）

笔者通过分析得知，学生出现以上错误的原因在于犯了“拿来主义”，将联想到的知识点拿来就用，知识体系不完备，没有找到问题的本质。

2.教师启发，转换思想

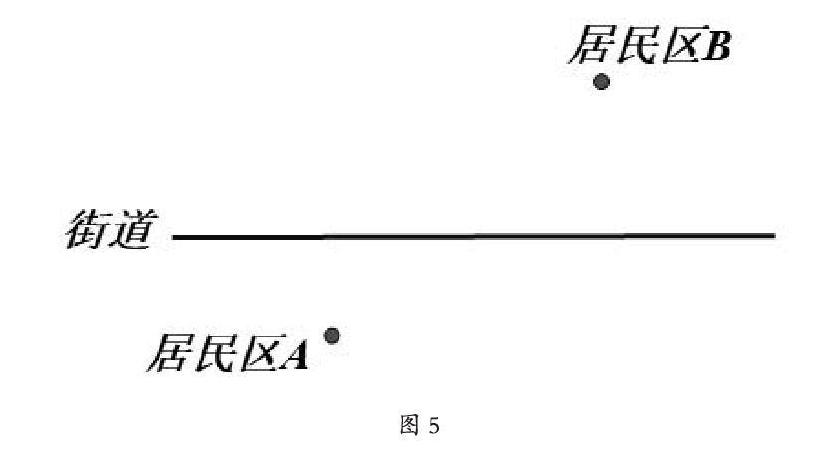
师：观察到A，B两点位于街道的同侧，我们尝试改变A，B两点的位置，使得两点位于街道的异侧。此时，奶站应建在何处？（教师使用几何画板，将居民区A的位置“拖”到街道的下方，如图5）

众生：连接A，B两点，线段A B与街道的交点就是所求的位置。

（教师根据学生的说法，在几何画板上操作画图，如图6）

师：很好！那么，我们这样操作的依据是什么？

生1：两点之间，线段最短。

师：正确！现在，我们将居民区A的位置“拖”回到街道的“上方”，此时，奶站应该建在何处？（如图7）

教学说明：将位于直线同侧两点的最短距离转化为求位于直线异侧两点的最短距离，将实际应用问题抽象为数学问题，化难为易，接近学生认知的“最近发展区”，渗透数学转化与化归思想，实现技能层面、思想方法层面上的功能。

3.比较学习，深化认知

生2：尝试找到A点关于街道的对称点A'，连接A'B，与街道的交点就是奶站所在的位置。

师：非常好！我们一起用尺规作图的方法将生2的画法画出来，那我们画图的第一步应该怎么做？

众生：画出A点关于街道的对称点A'。