基于强化学习的特征工程算法研究*
2021-08-02林珊玲林志贤郭太良
谢 斌 ,林珊玲 ,林志贤 ,郭太良
(1.福州大学 物理与信息工程学院,福建 福州 350116;2.中国福建光电信息科学与技术创新实验室,福建 福州 350116;3.福州大学 先进制造学院,福建 泉州 362200)
0 引言
机器学习广泛应用于人们的日常生活中,其中预测分析广泛应用于多个领域的决策,包括欺诈检测[1-2]、在线广告[3-4]、风险管理、市场营销等。预测模型是采用监督学习算法来进行预测,通过历史数据进行训练分类或者回归模型来预测未知的结果,以起到决策的作用。数据的表示方法对于模型的准确度十分重要,原始的数据空间往往难以表达数据。因此,在模型构建之前对数据进行适当的处理及转换是必不可少的。
特征工程的主要目的就是改变预测建模的特征以更好地适应算法的训练,通过生成那些判别性高的特征来提高模型训练的准确度。在现实中,特征工程是由数据科学家手动和根据领域知识来进行的,这一过程往往是十分繁琐且耗时的[5],而且很容易产生错误和偏差。
本文提出一种基于强化学习(RL)的方法进行特征工程,通过强化学习的相关方法从原始的数据中学习有效的策略。探索有效策略的过程无需人为的操作,通过算法自动学习得到。
1 相关工作
现有的特征工程的方法分为两种,一种使用数值变换方法进行特征工程。数据科学机(DSM)[6]提出和开发了深度特征综合算法,自动地为那些有关系的数据集生成特征;ExploreKit[7]通过原始特征中的信息来组合生成大量的候选特征,并提出了一种新颖的基于机器学习的特征选择方法;NARGESIAN U[8]提出训练一组神经网络,来预测对分类性能产生积极影响的转换。KHURANA U[9]通过对过去的示例进行强化学习,得出一种高效的探索策略;Cognit[10]系统以分层且非穷举的方式探索各种特征构造选择,通过贪婪的探索策略最大化模型的准确性;AutoCross[11]是用在表数据上的数据特征组合的方法,利用集束搜索策略构建有效的特征组合。
另一种是通过深度学习的方法来学习有用的特征。深度学习的方法在视频、图像以及语音等数据上取得巨大的成功,但是深度学习的方法往往需要大量的数据以避免过拟合,且其学习到的特征往往不可解释。
2 强化学习进行特征工程
本文的第一个贡献是将特征工程作为一个马尔可夫决策过程(MDP),令D0代表原始的特征空间,则状态空间S 就是经过一系列数字变换后形成的特征空间的集合。动作空间A 是一系列的数值变换方法(如sin、cos、log 等)的集合。当前特征空间D 经过特征变换a 后,新的特征空间D*=a(D),a∈A。
特征工程的主要目的是对原始数据进行一系列处理以获得最高的精度,所以MDP 过程中最终状态的奖励就是最终的特征空间与原始的特征空间的精度的差值,用Acc(D)来表示,令Π*作为在每一个状态选择动作的MDP 策略,DΠ代表从原始特征空间跟随Π*策略生成最终的特征空间。因此,Π*的作用就是使得Acc(DΠ)最大化,即在最终的状态空间获得最大的精度。

根据Bellman 的最优性原理[12],将最优值函数V*定义为:

所以最佳的策略Π*(D)可以定义为:

虽然上述的Π*可以得到最优的特征空间,但是状态空间S 的数量是指数级别的,处理起来将会十分困难。因此,本文第二个贡献是在上限置信区间算法(UCT)[13]的基础上提出一个近似的方法,使其可以用于进行二分类数值数据的特征工程,进而获得最优策略的近似值。
3 上限置信区间算法(UCT)
UCT 是一种蒙特卡洛树搜索算法,可以权衡勘探与利用,以探索最有希望的区域。算法分为4 个步骤:
(1)选择:从根节点开始,使用树策略即UCB 公式来挑选一个子节点,直到挑选到叶子节点。
(2)扩展:对选定的叶子节点,将叶子节点采取非试探性的动作可以达到的节点加入该叶子节点的子节点中。
(3)模拟:从当前选择的节点,根据预演策略来进行动作的选择直到模拟结束,得到的是一次蒙特卡洛实验并获得奖励值。
(4)回溯:用模拟过程得到的奖励值来更新当前节点及其所有的父亲节点的状态。
树策略(UCB)[14]公式为:
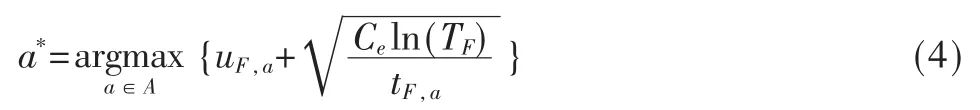
其中,TF是节点F 的访问次数,A 是可供选择的动作空间,uF,a表示节点F 选择动作a 时获得的平均奖励,tF,a表示节点F 选择动作a 的次数。参数Ce可用来控制勘探强度。
4 基于UCT 的特征工程
本文将特征工程视作蒙特卡洛树搜索过程,图1 为整体的结构示意图,图中只画出了3 层的结构图,动作空间为log、cos、sqrt。图中椭圆代表一个节点,每一个节点代表着不同版本的数据。节点与节点之间的连线代表选择的动作,状态空间就是这些节点的集合。其中D0是原始的特征空间也就是根节点,从根节点出发,每进行一次特征变换就会得到一个子节点。这样随着层数的不断增加,探索空间也呈现爆炸性增长。因此,遍历所有的节点是非常昂贵且不现实的,因此本文在UCT 的基础上提出求解最佳策略的方法,以此来权衡探索与利用。
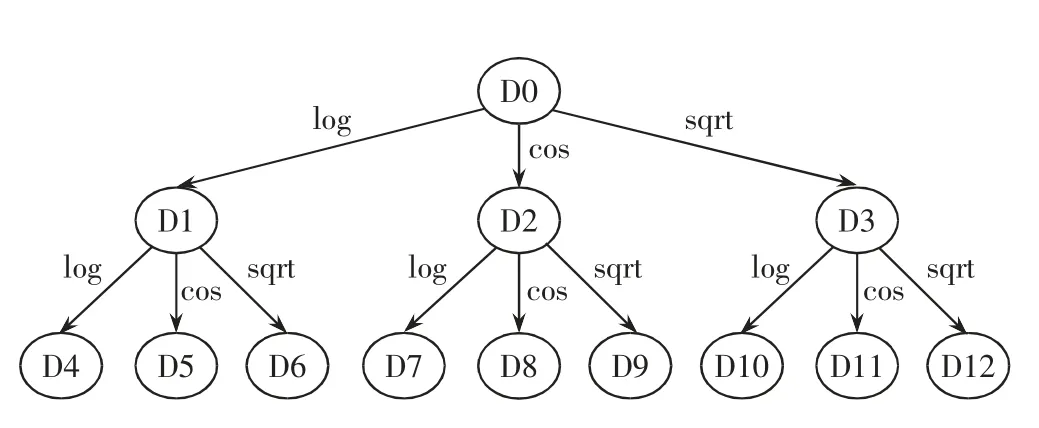
图1 整体结构示意图
本文在UCT 基础上提出一种近似方法,使其可以适用于特征工程。在UCT 中是根据平均收益来选择子节点。这在解决特征工程的问题并不是很适用,平均收益高的节点可以说明当前特征空间的特征是相对较好的,可能对于某些特征只有经过特定的变换才能获得较好的精度,但是在探索的过程中由于进行其他一些降低精度的变换,拉低了这个节点的奖励值,从而导致最终没有选择这个节点。因此,本文提出方法中节点中不仅维护了平均奖励、访问的次数,还维护了模拟过程中得到的最大的收益。在选择子节点时,根据子节点的最大收益值来进行选择。本文设定的实验结束的条件是达到最大的层数或者选择了停止动作。在达到最大的层数之前可能就已经获得了最佳的结果,停止动作的设立是为了避免这种情况发生。
接下来的部分是对本文在UCT 算法基础上提出的近似方法的介绍以及奖励函数、特征变换、模拟策略的描述。
4.1 奖励函数的设定
蒙特卡洛搜索要求每次迭代都要计算奖励值。奖励函数的主要目的就是判断变换的有效性,因此将最终的特征空间与原始特征空间的精度的差值作为奖励。设Ac 为特征空间的精度,本文计算的精度为FScore。D 为最终的特征空间,D0为原始的特征空间,则奖励R 可以表示为:

4.2 特征变换的设定(transform)
在进行特征变换时,设A 为动作空间,a∈A 为当前选择的动作,Di为当前的特征空间,则新的特征空间D*可以表示为:

特征变换都是对适合于当前选择的动作的特征进行变换。
在每次特征变换后通过特征筛选将特征的数量与原始特征空间保持一致,这样既可以使用判别性高的特征来创建高阶特征,又可以有效避免特征爆炸的问题。
4.3 模拟策略(evaluate)
本文设定的模拟策略为贪婪的策略,设A 为动作空间,D*为当前的特征空间。模拟策略Π*可以表示为:

在UCT 算法中模拟过程的节点往往是不会保存下来的,但是本文最终是根据子节点的最大收益来选择子节点。为了确保可以找到模拟过程中获得最大收益的路径,因此将模拟过程达到的节点全都保存下来。由于本文设定的是贪婪的模拟策略,需要昂贵计算代价,因此将模拟过程的节点保存下来在一定程度上会加快整体的计算速度。
(1)算法1 选择动作(get_act)


(2)算法2 本文近似算法

4.4 方法概述
算法1 展示了在每一层选择子节点的算法。通过UCB 公式来权衡探索与利用,以此来搜索最有希望的区域,同时在这过程中保存获得最大收益。最终通过最大的收益来选择子节点。这里判断循环结束的条件就是连续超过10 次选择相同的子节点或者达到最大的迭代次数。算法2 展示了本文提出的近似算法。在每一层通过算法1 来选择子节点,直到到达最终层或者挑选到停止动作。
5 实验和结果
本实验在5 个公开数据集上进行,验证本文提出方法的有效性。表1 列出了本文使用的5 个二分类数据集的名称、来源、记录数和特征的数量。
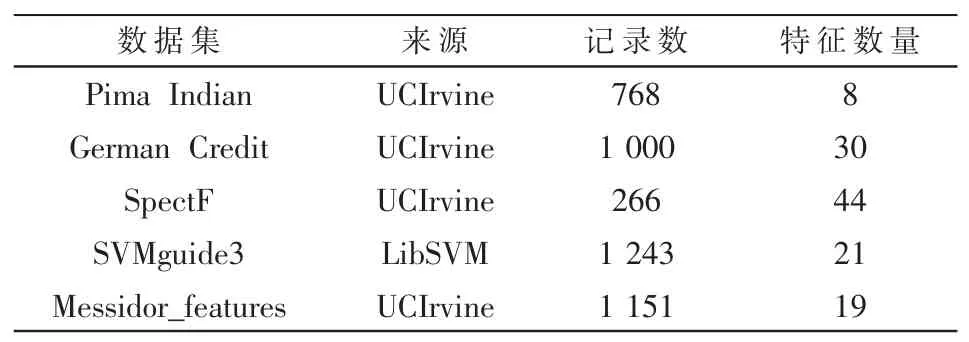
表1 本文使用5 个公开数据集的来源、记录数以及特征数量
所有的实验结果都是在5 折交叉验证下得到的,本文使用的模型是随机森林,模型的参数全部都是默认的参数。对于所有的数据集ce全部设为1.0。蒙特卡洛搜索树的最大层数设置为10 层,动作空间有:对数、开三次方、平方、开平方、标准化、归一化、S 函数、正弦、余弦、双曲函数、分桶、相加、相乘、停止14 种变换方法。在这些变换方法中相加和相乘的操作是对特征空间中的两两特征进行相加与相乘,停止操作就是不进行任何操作,返回原来的特征空间。
在实验中,比较了5 个方面的精度:(1)原始数据集;(2)本文的方法;(3)将所有特征变换方法都用在原始的特征空间后进行特征筛选;(4) 随机选择动作进行特征变换,重复进行10 次;(5)选择使当前特征空间获得最高精度的特征变换,重复进行10 次。比较结果如表2 所示。
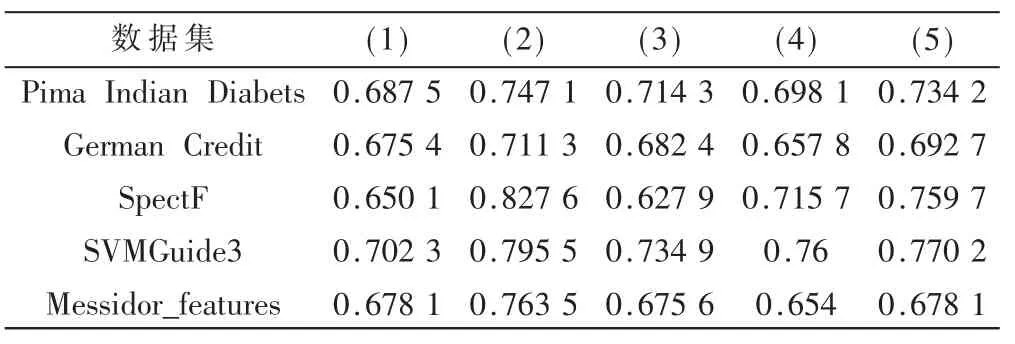
表2 各个数据集在五个方面的精度(FScore)比较
本文还与其他两篇有限元变换的特征工程文献[9-10]进行比较。这两篇文献和本文类似,都是使用数值变换来进行特征工程。文献[9]通过线性逼近的Q_learning[15]来从过去的示例来学习策略,而文献[10]则是使用制定好的策略。本文通过UCT 框架探索最佳的策略。本文使用FScore 提升量来进行比较,表3 中精度提升量以文献[9]为基准。

表3 本文方法与文献[9]、[10]FScore 提升量的比较
从表2 可以看出,本文提出的方法在5 个数据集原本的FScore 上平均提高了9.032%,在与其他变换方式进行比较时也是最好的。从表3 可以看出,本文提出的方法在除了German Credit 的数据集外,提升的精度是最高的。图2 展示了5 个数据集的FScore 与变换次数之间的关系,图中有些数据集变换不足10 次的原因是选择停止动作导致实验提前结束。对于搜索到最大层数的数据集的曲线走向整体上是朝上的,即使中间有较大的起伏,但是在最终层总能获得最高的精度。随着最大层数的加深,精度可能会进一步提升。最终层的特征的数量与原始特征空间的特征数量保持一致,在相同的特征数量下精度却得到了大幅度提升,说明本文提出的方法可以得到判别性高的特征,提高模型的学习能力,又能避免特征爆炸的问题,达到特征工程的目的。

图2 精度(FScore)与变换次数之间的关系
6 结论
本文中提出以一个新颖的思路将特征工程视作马尔可夫决策过程(MDP),在UCT 基础上提出一种特征工程的最佳策略的求解方法。本文提出的方法可以自动找到那些具有高判别性的特征,同时又避免了特征爆炸的问题,在5 个数据集上均取得了较好的效果。本文提出的方法目前只实现了二分类的数值数据的特征工程,还未支持多分类以及回归数据。由于采用的是贪婪模拟策略,所需要的计算代价比较昂贵,也有可能陷入局部最优的情况。未来可以通过深度蒙特卡洛的方法作为特征工程求解的方法,将深度学习的方法与蒙特卡洛的方法相结合来实现特征工程。
