环Fq+uFq+vFq上(1-2u-2v)-常循环码和量子码的构造

2021-08-02李兆龙朱士信

合肥工业大学学报(自然科学版) 2021年7期

李兆龙, 朱士信

(合肥工业大学数学学院,安徽合肥 230601)

0 引言

文献[1]提出量子码,其在量子计算中有良好的纠错能力;文献[2]提出基于经典码构造量子码的方法,即CSS构造方法。后来量子码的构造被推广到非二元情形[3-4]。此后,编码理论界通过有限域上各种经典码,如RS码[5]、BCH码[6]、常循环码[7-9]等,构造了一系列量子码。

随着编码理论的发展,基于有限环上经典码构造量子码的方法受到广泛关注。文献[10]基于环F2[u]/(u2)上循环码构造了量子码;文献[11]基于环F4[u]/(u2)上循环码构造了参数较优的二元量子码;文献[12]基于环F2m[u]/(uk+1)上循环码构造了参数较优的2m元的量子码;文献[13]基于环Fp2m[u]/(u2)上循环码构造了参数较优的pm元量子码。此后,基于有限非链环上经典码的量子码构造方法同样受到广泛的关注。文献[14]基于非链环F2[v]/(v2-v)上循环码构造了二元量子码;文献[15]基于非链环Fp[v]/(v2-v)上的循环码构造了p元量子码;文献[16]基于非链环Fp[v]/(v3-v)构造了p元量子码;文献[17-18]基于非链环Fq+uFq+vFq+uvFq上经典码,通过选取不同的Gray映射,分别构造了p元量子码。最近,文献[19]基于非链环F2+uF2+vF2上循环码构造了二元量子码,其中u2=u,v2=v且uv=vu=0。以上结果表明,基于非链环上经典码可以构造参数较优的量子码。受此启发,本文将基于环R=Fq+uFq+vFq上常循环码构造量子码,其中q是一个奇素数幂,u2=u,v2=v且uv=vu=0。

环R是一个主理想环,它有3个极大理想(1-u)、(1-v)和(u+v)。文献[20]利用代数的方法分别研究了环R上的线性码和斜循环码的代数结构。本文基于环R的直和分解研究该环上(1-2u-2v)-常循环码,并将其应用于量子码的构造。

1 预备知识

设p>3是一个素数,m是一个正整数且q=pm。设R=Fq+uFq+vFq,Fq表示q阶有限域,u和v满足关系u2=u,v2=v且uv=vu=0,则环R是一个阶为q3的有限非链环。设e1=1-u-v,e2=u和e3=v,则e1、e2和e3是环R上一组本原幂等元。由中国剩余定理得:

R=e1Fq⨁e2Fq⨁e3Fq,

其中,⨁表示环R的直和。

环R中的每个元素r可唯一分解为:

r=e1r1+e2r2+e3r3,

其中,ri∈Fq。

设Rn是环R上n-元组集合。Rn中的每个n-元组c可以唯一表示为:

c=e1c1+e2c2+e3c3,

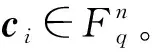
(λcn-1,c0,…,cn-2)∈C。

通常,将(c0,c1,…,cn-1)∈Rn等同于

c0+c1x+…+cn-1xn-1∈R[x]/(xn-λ),

其中,R[x]/(xn-λ)表示多项式环R[x]关于理想(xn-λ)的商环。在这个意义下,C是环R上码长n的λ-常循环码当且仅当C是环R[x]/(xn-λ)的理想。

对于Rn中的任意2个n-元组,即a=(a0,a1,…,an-1)和b=(b0,b1,…,bn-1),它们的内积定义为:

a·b=a0b0+a1b1+…+an-1bn-1。

若a·b=0,则称a和b是正交的。对于环R上码长n的线性码C,称

C⊥={b∈Rn|a·b=0,∀a∈C}

为C的对偶码。若C⊆C⊥,则称C是自正交码。

设C是环R上长度n的线性码,定义:

e1a+e2b+e3c∈C};

ε1a+ε2b+ε3c∈C};

则有C=e1C1⨁e2C2⨁e3C3。其中,C1、C2、C3为Fq上线性码且|C|=|C1||C2||C3|。

设Ci的生成矩阵为Gi,则C的生成矩阵G为:

其中,GT为矩阵G的转置矩阵。

2 Gray映射

命题1 当p>3时,φ是一个双射。

(1)

有解。因为方程组(1)的系数矩阵的秩为3,方程组(1)有解,所以φ是一个满射。

对环R中的元素r,定义它的Gray重量为:

wtG(r)=wtH(φ(r)),

φ:a|→(φ(a0),φ(a1),…,φ(an-1)),

其中,a=(a0,a1,…,an-1)∈Rn。定义a的Gray重量为:

对任意a、b∈Rn,a和b的Gray距离定义为:

dG(a,b)=wtG(a-b)。

环R上码长n的线性码C的Gray距离定义为R中任意2个不同码字Gray距离的最小值。

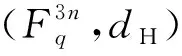
证明因为对Rn中任意元素a=(a0,a1,…,an-1)和b=(b0,b1,…,bn-1),Fq中的任意元素m、n,有

φ(ma+nb)=

(φ(ma0+nb0),φ(a1+nb1),…,

φ(an-1+nbn-1))=

(mφ(a0)+nφ(b0),mφ(a1)+nφ(b1),…,

mφ(an-1)+nφ(bn-1))=mφ(a)+nφ(b),

所以φ是Fq-线性的,且由Gray距离和Gray重量的定义可得:

dG(a,b)=wtG(a-b)=

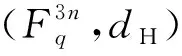
由命题2易证下列命题成立。

近年来，随着老龄化的加重，高血压、糖尿病等慢性疾病的增加，每年新增的脑卒中患者有200万人，其中会有70%～80%的患者会因疾病问题导致肢体运动出现障碍，从而影响生活质量，为家庭带来沉重的经济负担。脑卒中属于急性脑血管疾病，在中医当中属于“中风中的痿痹”，多是由于患者机体衰老，气血亏虚，脑髓失养，引起肝阳上亢，情志不畅等原因从而导致肝气瘀滞，痹阻于脑脉而引发病的疾病。因此改善脑卒中偏瘫患者肢体运动功能、提高患者的生活质量，是目前关注的主要问题。

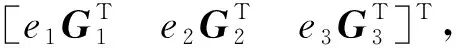
命题4 设C是环R上码长n的线性码,则φ(C)是Fq上码长3n的自正交码当且仅当码C是自正交的。

a·b=e1a1·b1+e2a2·b2+e3a3·b3=0。

由此推出a1·b1=a2·b2=a3·b3=0。

另一方面,由Gray映射的定义可得:

φ(a)·φ(b)=9[a1·b1+a2·b2+a3·b3]。

于是φ(a)·φ(b)=0,即φ(a)与φ(b)正交。

再结合a和b的任意性知,φ(C)是Fq上码长3n的自正交码。

3 量子码的构造

本节以环R上码长n的(1-2u-2v)-常循环码为载体构造量子纠错码。

引理1[2]设C是Fq上参数为[n,k,d]的线性码,若C⊥⊆C,则存在参数为[[n,2k-n,d]]的q元量子码。

证明首先证明必要性。设ai=(ai,0,ai,1,…,ai,n-1)是Ci的任意一个码字,i=1,2,3。令

b=(b0,b1,…,bn-1)=e1a1+e2a2+e3a3,

则b∈C。

因为C是(1-2u-2v)-常循环码,所以((1-2u-2v)bn-1,b0,…,bn-2)∈C。因为

(1-2u-2v)bn-1=e1a1,n-1-e2a2,n-1-e3a3,n-1,

所以

(a1,n-1,a1,0,…,a1,n-2)∈C1,

(-a2,n-1,a2,0,…,a2,n-2)∈C2,

(-a3,n-1,a3,0,…,a3,n-2)∈C3。

于是C1是Fq上码长n的循环码,C2和C3是Fq上码长n的负循环码。

然后证明充分性。设b=(b0,b1,…,bn-1)=e1a1+e2a2+e3a3是码C的任意一个码字,其中

ai=(ai,0,ai,1,…,ai,n-1),i=1,2,3。

由定义知ai∈Ci,

(a1,n-1,a1,0,…,a1,n-2)∈C1,

(-a2,n-1,a2,0, …,a2,n-2)∈C2,

(-a3,n-1,a3,0,…,a3,n-2)∈C3。

由此得:

(e1a1,n-1-e2a2,n-1-e3a3,n-1,b0,…,bn-2)∈C,

即((1-2u-2v)bn-1,b0,…,bn-2)∈C。由b的任意性知,C是环R上码长n(1-2u-2v)-常循环码。

引理4[2]设C是Fq上生成多项式为g(x)的循环码或负循环码。则C⊥⊆C的充要条件是xn-λ≡0(modg(x)g*(x)),其中：λ∈{1,-1};g*(x)为g(x)的互反多项式。

基于以上引理可得如下结论:

定理1 设C是环R上码长n生成多项式为g(x)=e1g1(x)+e2g2(x)+e3g3(x)的(1-2u-2v)-常循环码,则C⊥⊆C的充要条件为:

证明首先证明充分性。由引理4知,当

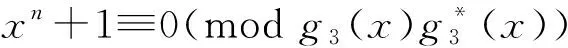
然后证明必要性。若C⊥⊆C,则

结合引理4,结论成立。

证明由引理1和定理1可证得定理2的结论。

下面基于环R上(1-2u-2v)-常循环码构造量子码。

例1 设q=5。在Fq上,x15-1=(x+4)5×(x2+x+1)5,x15+1=(x+1)5(x2+4x+1)5。设C是环R=F5+μF5+νF5上码长15生成多项式为g(x)=e1(x+4)+e2(x2+4x+1)+e3(x2+2x+1)的(1-2u-2v)-常循环码,即g1(x)=x+4、g2(x)=x2+4x+1和g3(x)=x2+2x+1满足定理1的条件。

容易验证,φ(C)是Fq上参数为[45,40,3]的线性码。

由定理2知,存在参数为[[45,35,≥3]]的5元量子码,比文献[16]中参数[[45,33,≥3]]的5元量子码有更大的维数。

例2 设q=5。在Fq上,

x30-1=(x+1)5(x+4)5×

(x2+x+1)5(x2+4x+1)5,

x30+1=(x+2)5(x+3)5×

(x2+2x+4)5(x2+3x+4)5。

设C是环R=F5+μF5+νF5上码长30生成多项式为g(x)=ε1(x2+x+1)+ε2(x+2)+ε3(x+3)2的(1-2u-2v)-常循环码,即g1(x)=x2+x+1、g2(x)=x+2和g3(x)=(x+3)2满足定理1的条件。

容易验证,φ(C)是Fq上参数为[90,85,3]的线性码。由定理2知,存在参数为[[90,80,≥3]]的5元量子码,比文献[16]中参数[[90,78,≥3]]的5元量子码有更大的维数。

例3 设q=5。在Fq上,

x31-1=(x+4)(x3+x+4)×

(x3+2x+4)(x3+x2+x+4)×

(x3+x2+3x+4)(x3+2x2+x+4)×

(x3+2x2+4x+4)(x3+3x2+4)×

(x3+4x2+4)(x3+4x2+3x+4)×

(x3+4x2+4x+4),

x31+1=(x+1)(x3+x+1)×

(x3+2x+1)(x3+x2+1)×

(x3+x2+3x+1)(x3+x2+4x+1)×

(x3+2x2+1)(x3+3x2+x+1)×

(x3+3x2+4x+1)(x3+4x2+x+1)×

(x3+4x2+3x+1)。

设C是环R=F5+μF5+νF5上长31生成多项式为ε2(x3+ε2(x3+3x2+4x+1)+ε3(x3+x2+3x+1)的(1-2u-2v)-常循环码,即g1(x)=x3+x2+3x+1、g2(x)=x3+3x2+4x+1和g3(x)=x3+x2+3x+1满足定理1的条件。

容易验证,φ(C)是Fq上参数为[93,84,4]的线性码,由定理2知,存在参数为[[93,75,≥4]]的5元量子码,比文献[16]中参数[[93,75,≥2]]的5元量子码拥有更大的极小距离。

例4 设q=5。在Fq上,

x12+1=(x2+2)(x2+3)(x2+x+2)×

(x2+2x+3)(x2+3x+3)(x2+4x+2),

x12-1=(x+1)(x+2)(x+3)×

(x+4)(x2+x+1)(x2+2x+4)×

(x2+3x+4)(x2+4x+1)。

设C是环R=F5+μF5+νF5上码长12生成多项式g(x)=ε1(x2+2x+4)+ε2(x2+3x+3)+ε3(x2+3x+3)的(1-2u-2v)-常循环码,即g1(x)=x2+2x+4、g2(x)=x2+3x+3和g3(x)=x2+3x+3满足定理1的条件。

容易验证,φ(C)是Fq上参数为[36,30,3]的线性码。由定理2知,存在参数为[[36,24,≥3]]的5元量子码,比文献[16]中参数[[40,24,≥2]的5元量子码有更大的码率和极小距离。

例5 设q=5。在Fq上,

x28+1=(x2+2)(x2+3)×

(x6+x5+4x4+3x3+2x2+4x+2)×

(x6+2x5+x4+4x3+2x2+3x+3)×

(x6+3x5+x4+x3+2x2+3x+3)×

(x6+4x5+4x4+2x3+2x2+x+2),

x28-1=(x+1)(x+2)(x+3)×

(x+4)(x6+x5+x4+x3+x2+x+1)×

(x6+2x5+4x4+3x3+x2+2x+4)×

(x6+3x5+4x4+2x3+x2+3x+4)×

(x6+4x5+x4+4x3+x2+4x+1)。

设C是环R=F5+μF5+νF5上码长28生成多项式为g(x)=ε1(x6+2x5+4x4+3x3+x2+2x+4)+ε2(x6+3x5+x4+x3+2x2+2x+3)+ε3(x6+2x5+x4+4x3+2x2+3x+3)的(1-2u-2v)-常循环码,即g1(x)=x6+2x5+4x4+3x3+x2+2x+4、g2(x)=x6+3x5+x4+x3+2x2+2x+3和g3(x)=x6+2x5+x4+4x3+2x2+3x+3满足定理1的条件。

容易验证,φ(C)是Fq上参数为[84,66,3]的线性码。由定理2知,存在参数为[[84,48,≥3]]的5元量子码,比文献[17]中参数[[88,48,≥2]的5元量子码有更大的码率和极小距离。

例6 设q=5。在Fq上,

x44+1=(x2+2)(x2+3)×

(x10+x8+x6+2x4+x2+2)×

(x10+2x8+x6+2x4+3x2+2)×

(x10+3x8+x6+3x4+3x2+3)×

(x10+4x8+x6+3x4+x2+3),

x44-1=(x+1)(x+2)(x+3)×

(x+4)(x5+x4+x3+2x2+x+2)×

(x5+x4+4x3+4x2+3x+1)×

(x5+2x4+x3+2x2+3x+2)×

(x5+2x4+4x3+x2+x+4)×

(x5+3x4+x3+3x2+3x+3)×

(x5+3x4+4x3+4x2+x+1)×

(x5+4x4+x3+3x2+x+3)×

(x5+4x4+4x3+x2+3x+4)。

设C是环R=F5+μF5+νF5上码长44生成多项式为g(x)=ε1(x+1)+ε2(x2+2)+ε3(x2+3)的(1-2u-2v)-常循环码,即g1(x)=x+1、g2(x)=x2+2和g3(x)=x2+3满足定理1的条件。

容易验证,φ(C)是Fq上参数为[132,127,2]的线性码。由定理2可知,存在参数为[[132,122,≥2]]的5元量子码,比文献[6]中参数[[132,92,≥2]的5元量子码有更大的维数。

例7 设q=11。在Fq上,

x20+1=(x2+x+6)(x2+2x+2)×

(x2+3x+10)(x2+4x+8)(x2+5x+7)×

(x2+6x+7)(x2+7x+8)(x2+8x+10)×

(x2+9x+2)(x2+10x+6),

x20-1=(x+1)(x+2)(x+3)×

(x+4)(x+5)(x+6)(x+7)(x+8)×

(x+9)(x+10)(x2+1)(x2+3)×

(x2+4)(x2+5)(x2+9)。

设C是环R=F11+μF11+νF11上码长20生成多项式为g(x)=ε1(x+3)(x+6)(x+9)+ε2(x2+2x+2)(x2+3x+10)+ε3(x2+5x+7)的(1-2u-2v)-常循环码,即g1(x)=(x+3)(x+6)(x+9)、g2(x)=(x2+2x+2)×(x2+3x+10)和g3(x)=x2+5x+7满足定理1的条件。

容易验证,φ(C)是Fq上参数为[60,51,5]的线性码。由定理2知,存在参数为[[60,42,≥5]]的5元量子码,比文献[17]中参数[[60,40,≥5]的5元量子码有更大的维数。