含旋转部件的动态目标ISAR成像及微多普勒特征提取*
2021-08-02赵东涛黄雁飞齐玉涛
赵东涛, 黄雁飞, 齐玉涛
(1. 中国飞行试验研究院, 陕西西安 710089; 2. 中航西飞民用飞机有限责任公司, 陕西西安 710089)
0 引言
在逆合成孔径雷达(ISAR)成像时,通常假设目标满足刚体模型,即认为目标上所有散射点运动状态是相同的。但是,对含有微动特征信息的目标,相对于主体部分存在高速旋转, 由于不满足刚体假设条件,其旋转部件将在图像中表现为沿多普勒方向的调制干扰,造成目标主体成像模糊[1-2]。为获得目标完整、准确的成像特征描述信息,需要根据回波特征对旋转部件和目标主体回波分离,一方面可以提高二维成像中目标主体结构的成像质量,获得目标的精细结构特征信息[3],另一方面可提高微多普勒信号的微动参数估计精度,反演目标的运动和结构信息,作为目标识别的重要依据[4]。
Chen提出微多普勒概念以来,许多有效的微多普勒信号分离技术相继被提出。小波变换分离活动部件及目标,通过剔除活动部件对成像结果的影响,提取清晰的散射中心,但是小波变换是一种时频面上机械的格型分解,其本质上无自适应性[5];基于Chirplet 基分解的分离方法,依据调频率参数的大小对微多普勒信号进行分离,该方法对喷气式飞机实测数据处理,取得了不错的分离结果,但是,Chirplet 基函数包含4 个未知参数,分解算法运算量较大[6];基于Radon变换的目标主体信号与微动信号分离方法,对回波信号进行时频变换,然后在时频平面上通过Radon变换来分离目标主体信号与微动信号,该方法对仿真数据取得较好的分离结果,但是对实测数据效果不明显[7]。
本文利用目标主体信号稳定、多普勒频率慢变化,而旋转部件信号非平稳、多普勒频率快变化的特性,采用时频分析的技术将信号的时频分布在时间维上按模值大小重新排列,设置门限剔除模值大的元素,从而将非平稳信号剔除,实现主体和微动信号的分离。但是在剔除非平稳信号过程中难免有主体回波损失,针对该情况,文中采用循环自适应的方式进行多次迭代,当剩余信号的总能量低于一定门限时迭代停止,认为剩下的成分就是目标主体的回波,从而实现目标主体回波和旋转部件回波的分离。通过将旋转部件回波和目标主体回波分离,可以提高目标主体的成像质量,对微动信号作单独分析,能更好地获得旋转部件的微动特征参数[8-9]。
1 含旋转部件目标回波成像模型
含旋转部件目标ISAR成像转台模型示意图如图1所示,假定目标主体的平动已经补偿并转化为转台模型,xoy和x′o′y′分别为刚体目标和旋转目标的坐标系,刚体散射点A(xA,yA)围绕刚体坐标系原点O作角速度为ω0的匀速旋转运动,旋转目标散射点B(xB,yB)除了绕转台中心作角速度为ω0的匀速旋转,还围绕旋转目标坐标系原点O′以自转角速度ω′0作匀速旋转运动,两种转动的角速度关系ω′0≫ω0。
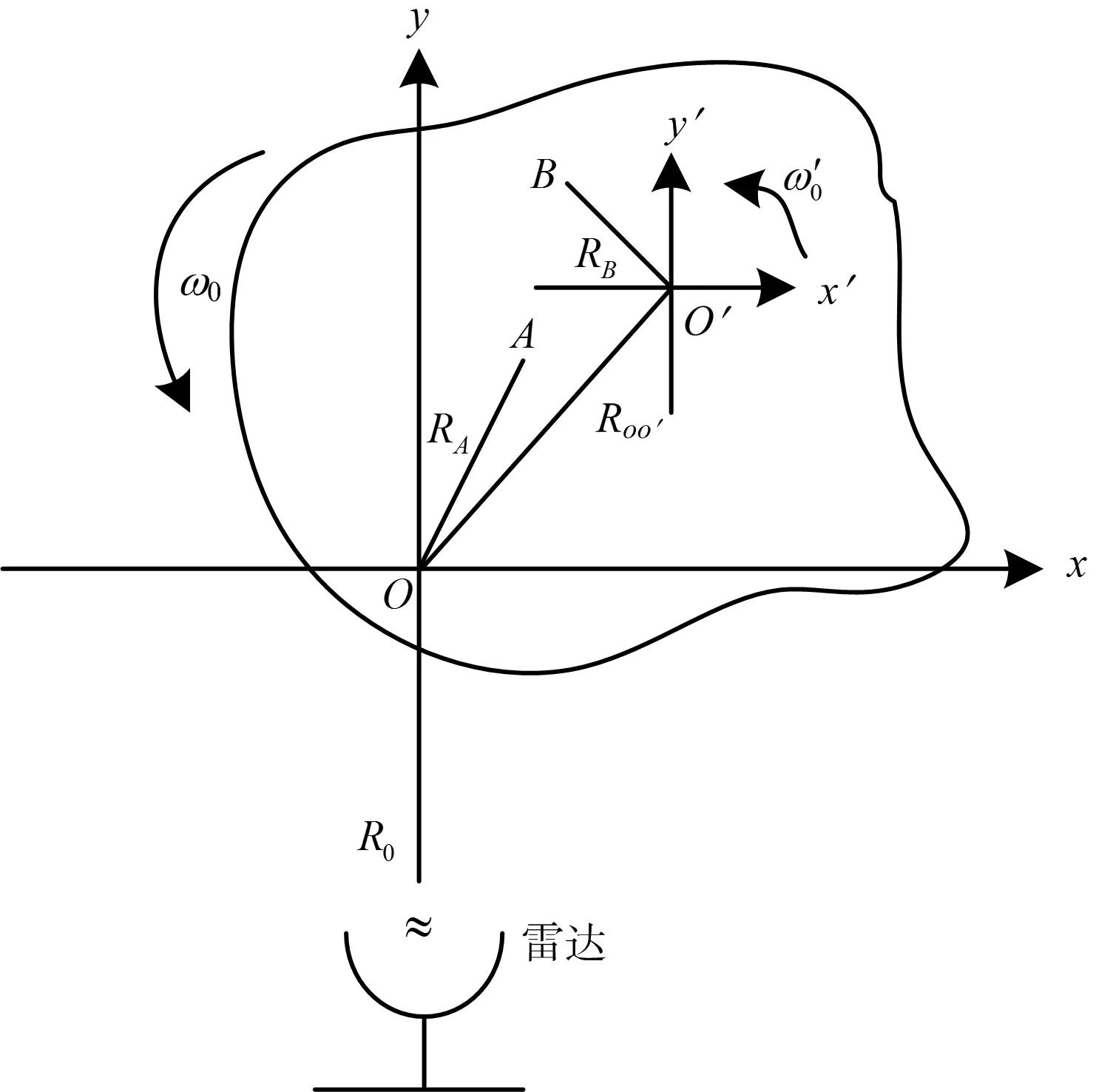
图1 含旋转部件ISAR转台模型示意图
设雷达发射的线性调频信号如式(1)所示:
(1)
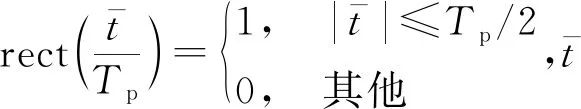
目标上第i个散射点的回波如式(2)所示:
(2)
式中,σ(tm)为目标后项散射系数,c为光速。以坐标原点O为参考距离构造参考信号如式(3)所示:
(3)
采用解线性调频(Dechirp)信号处理方法,即
(4)
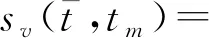
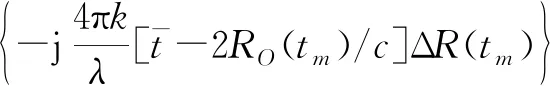
(5)
式中,λ为波长,ΔR(tm)=R(tm)-RO(tm)。
在快时间域对Dechirp处理之后的信号进行距离压缩,可得如式(6)所示:
sv(f,tm)=σ(tm)Tp·
(6)
刚体散射点A和坐标原点O之间距离满足:
ΔRA(tm)=RAsin(ω0tm)
(7)
由于RO O′≪RO和RB≪RO,旋转部件散射点B和坐标原点O之间的距离如式(8)所示:
ΔRB(tm)=RO O′sin(ω0tm)+RBsin(ω′0tm)
(8)
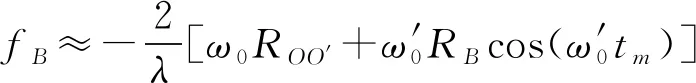
2 基于时频分析的微动特征信号分离算法
微动特征信号分离算法思路是利用主体回波信号稳定、多普勒频率慢变化,而旋转部件回波信号非平稳、多普勒频率快变化的特性,采用时频分析技术去除微多普勒效应的方法,实现机身主体回波和机翼旋转部件回波的分离。具体步骤如下:
步骤1: 将包络对齐后回波数据按距离单元存储构成二维矩阵,行为同一距离单元不同发射脉冲的回波,列为每一个发射脉冲按距离单元存储的回波;
步骤2: 每个距离单元作短时傅里叶变换(STFT)如式(9)所示:
(9)
式中,ω(i)为窗函数,k表示第k个距离单元,对于固定的频率Ω,考虑到含有M个元素的集合,即
Sk(m)={STFTk(m,Ω),m=0,1,…,M-1}
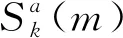
步骤4: 对于含有微动特征信息的STFT的变换结果按照模的大小重新排列,得到排列之后的结果:|φk(0)|≤|φk(1)|≤…≤|φk(M-1)|;
步骤5: 取固定的门限值Q%(Q一般取10~15),采用循环自适应的方式进行多次迭代,剔除STFT中幅度较大的值,保留单频信号;
步骤6: 将各个距离单元剩下的元素沿着时间轴进行累加,得到去除微多普勒效应后的刚体散射点的频谱。微动特征信号分离流程如图2所示。
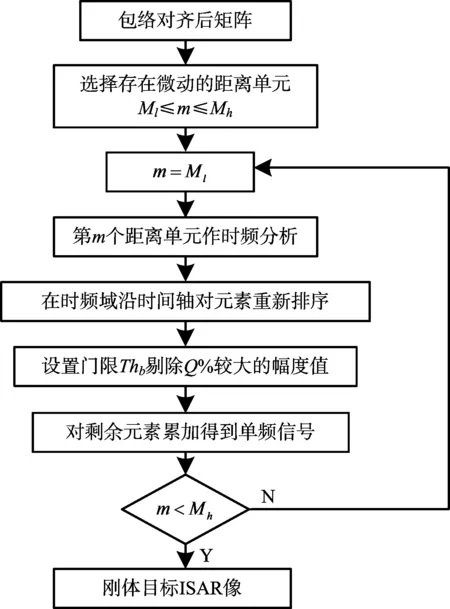
图2 微动特征信号分离流程图
3 微动信号分离后特征提取方法
由于旋转部件微动具有周期性的简谐振动,周期性的旋转导致雷达回波调制亦具有周期性,因此可利用回波相关法估计旋转部件微动的周期和频率。假设旋翼叶片回波s(t)的离散表示为s(n),其中n=1,2,…,N表示时域回波第n个时间点,N为时域回波信号点数,则回波自相关如式(10)所示:
(10)
由函数相关特性可知,R[m]在回波周期的整数倍处出现峰值,可反映回波的周期性,根据R[m]峰值之间的间距可以得到信号的周期估计结果,假设时间采样间隔为Δt,那么周期估计结果表示如式(11)所示:
T=|m1-m2|Δt
(11)
式中,m1和m2分别表示相邻两个峰值的位置,则微动转动频率估计表示为F=1/T。
4 算法仿真分析
假设目标散射点模型由5个散射点组成,第1,2,3,4为主体射点,第5个散射点为主体散射点上附加旋转散射点,旋转频率为25 Hz,散射点分布如图3所示。设雷达发射线性调频(LFM)信号,载频为9.5 GHz,带宽为1 GHz,脉宽为50 μs,脉冲重复频率为1 kHz,成像积累脉冲数为512个。
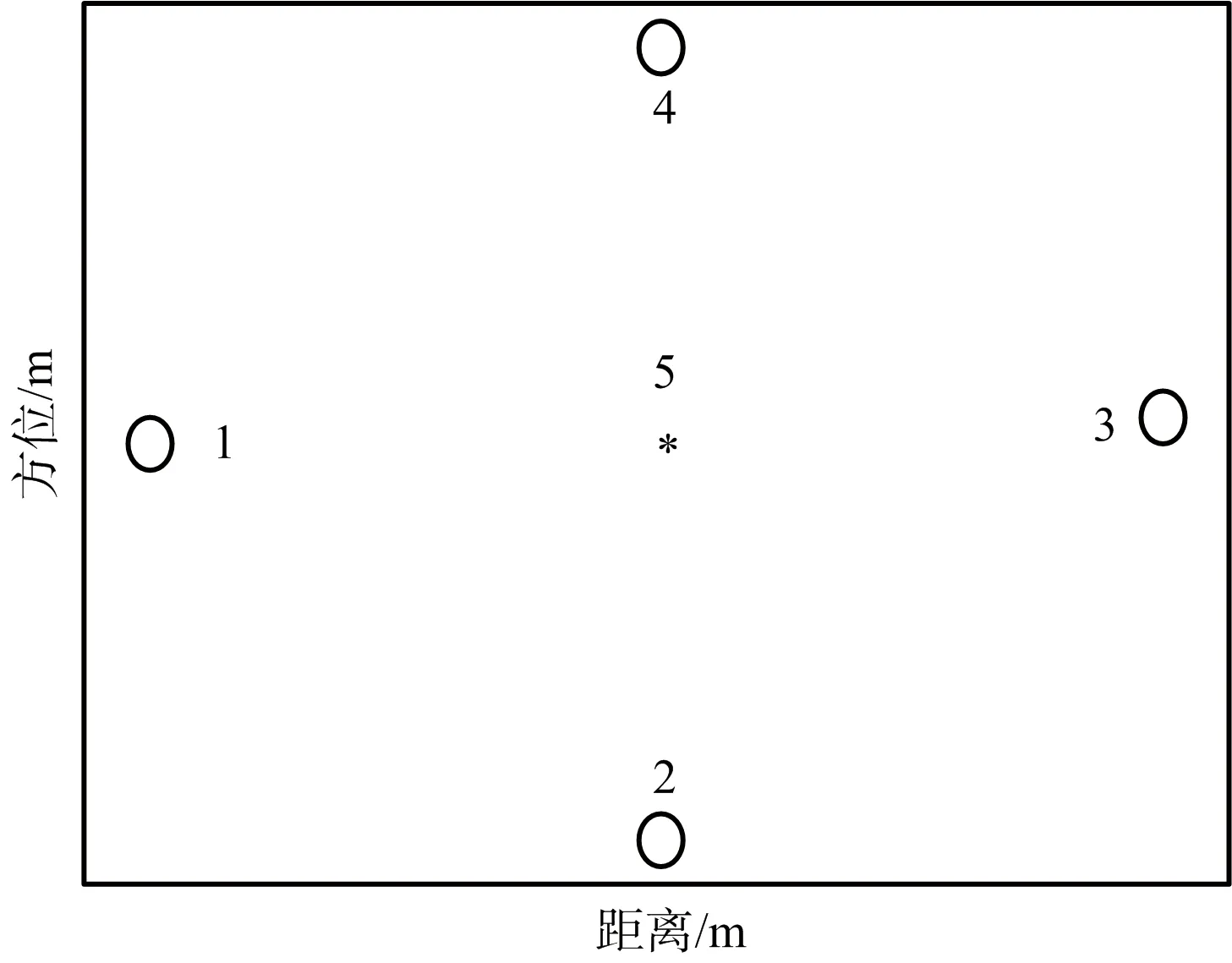
图3 目标散射点分布示意图
仿真过程中,向回波中加入高斯白噪声,信噪比SNR=0 dB。对目标回波数据处理得到的ISAR 成像结果如图4所示,从图4可以看出,由于旋转散射点5在第235个距离单元,该距离单元受到微多普勒调制的影响,使得主散射点1,3和5淹没在调制带中,掩盖了主散射点。对该距离单元进行STFT得到其时频图如图5所示,从图5可以看出,回波信号的瞬时多普勒包含3条直线和1条正弦曲线,分别对应该距离单元内目标3个主体散射点和1个旋转散射点。对该距离单元回波STFT后数据按照模的大小进行排列,分离STFT中幅度较大的值,保留单频信号,实现旋转部件成像和目标主体成像分离,分别如图6和图7所示。对分离后的微多普勒信号作自相关处理得到旋转部件的旋转周期,如图8所示,此处求出旋转周期为0.04 s,与旋转频率为25 Hz一致。
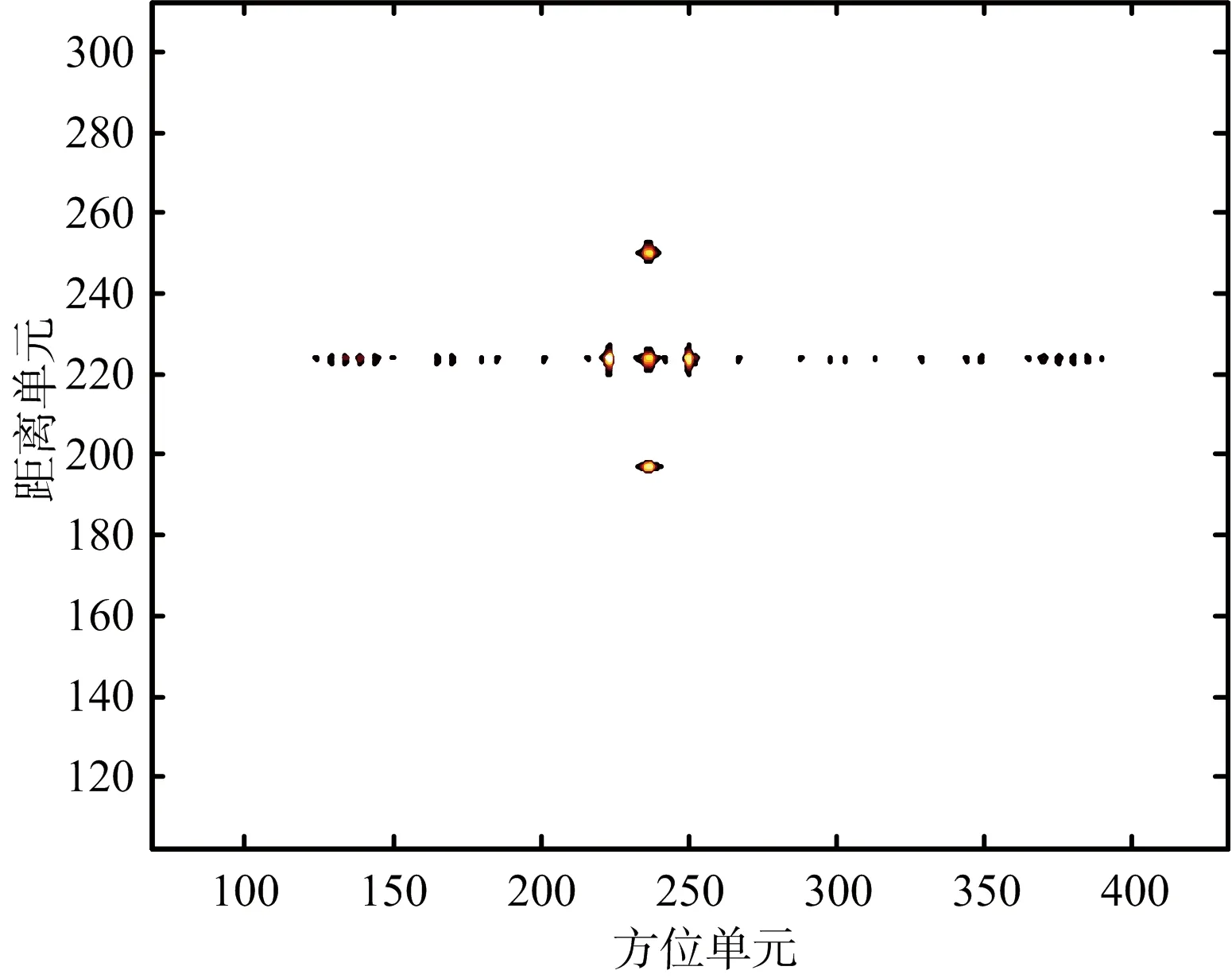
图4 目标回波ISAR成像

图5 第235个距离单元回波的STFT

图6 分离后目标主体部件的ISAR像

图7 分离后目标旋转部件的ISAR像
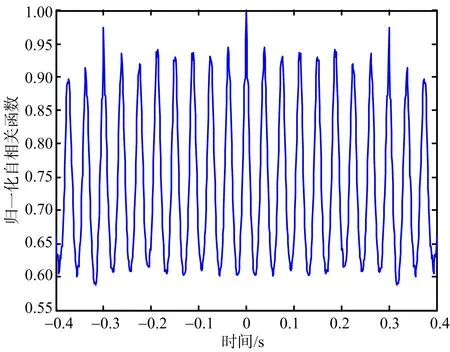
图8 分离后第235个距离单元信号自相关
5 实测数据分析
以运七螺旋桨飞机雷达实测数据进行分析,验证算法对实测数据的有效性。测量雷达工作在X波段,发射LFM信号,雷达载频为9.5 GHz,带宽为1 GHz,脉宽为50 μs,脉冲重复频率为1 kHz,成像积累脉冲数为512。运七飞机实测数据ISAR图像如图9所示,从图9可以看出,螺旋桨的旋转带来ISAR成像中的条带干扰,由于螺旋桨相对于转台中心的角速度很大,无法将其散射点位置聚焦到方位的坐标,形成贯穿整个距离门的条带,在第238个距离单元附近产生两个展宽的微多普勒带。采用上述方法对微多普勒信号和目标主体回波进行分离,分别如图10和图11所示,从图10可以看出,去除微动信号后能够清楚看到目标主体二维图像,从图11可以看出,分离出的微动信号调制频率与目标ISAR图像中的频率一致,成功地实现了微动信号与主体信号分离。通过对比微多普勒分离前后的目标ISAR 像,可以看出,经该方法对实测数据进行微多普勒分离,能获得聚焦的主体图像。对第238个距离单元微多普勒信号分离前后的自相关函数分别如图12和图13所示,从图中可以看出,分离前微动信号叠加在目标主体部分之上,微动特征不是很明显,而分离后微特征信息比较明显,与飞机实际螺旋桨调制周期一致。通过对比微多普勒分离前和分离后的目标ISAR 像及微多普勒特征信息,可看出该方法对实测数据微多普勒分离有效,可以获得聚焦的主体图像,且有利于更准确地估计出旋转部件的微动参数,可用于不同类型飞机目标的分类和识别。
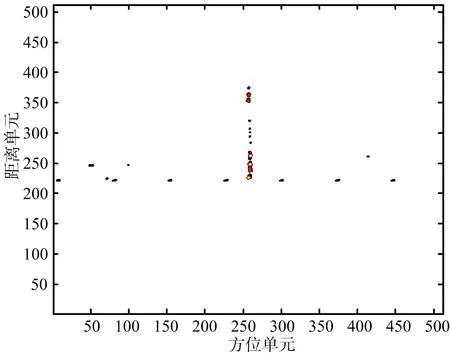
图9 目标回波数据ISAR像
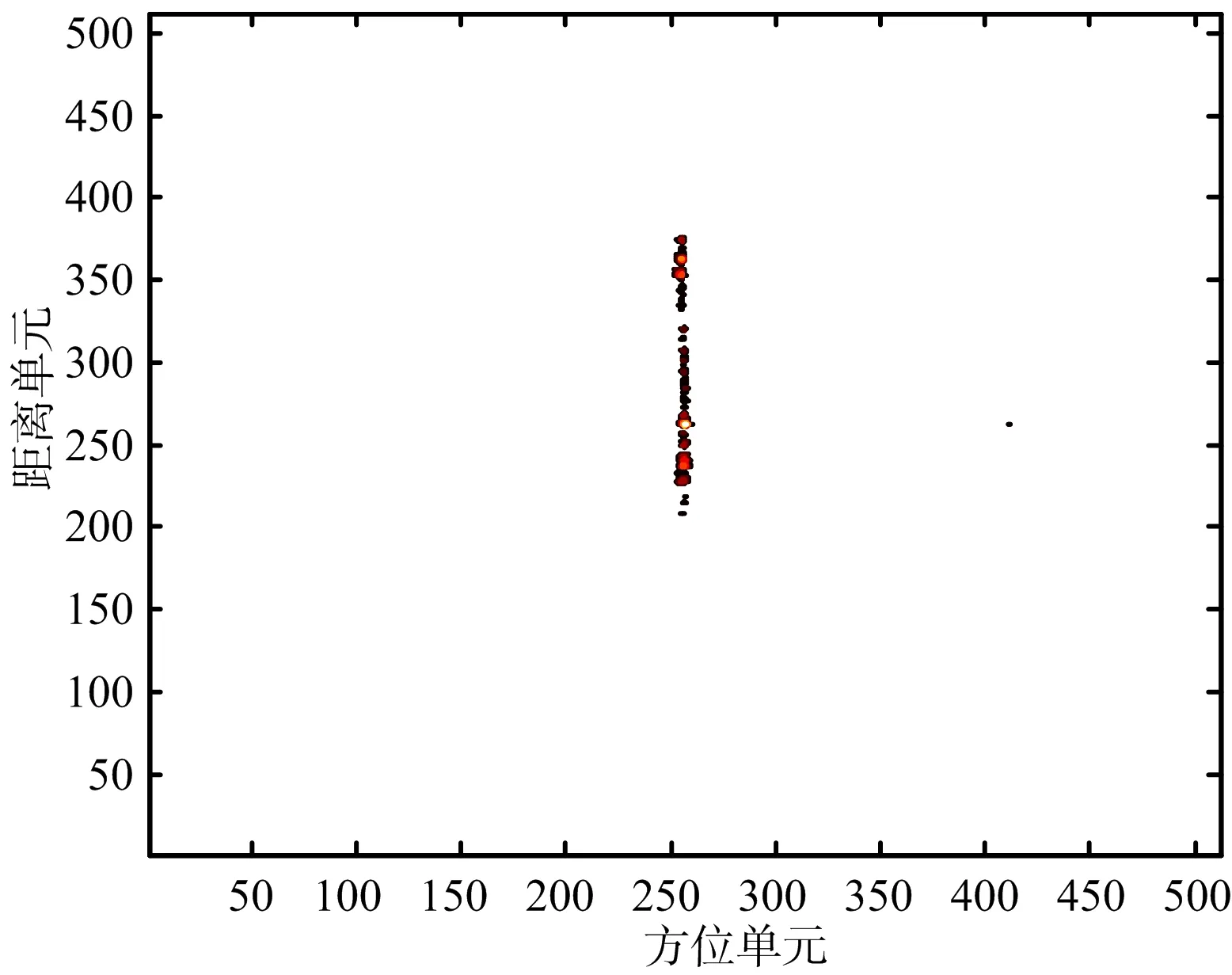
图10 分离后目标主体部件的ISAR像

图11 分离后目标旋转部件的ISAR像

图12 分离前第238个距离单元信号自相关
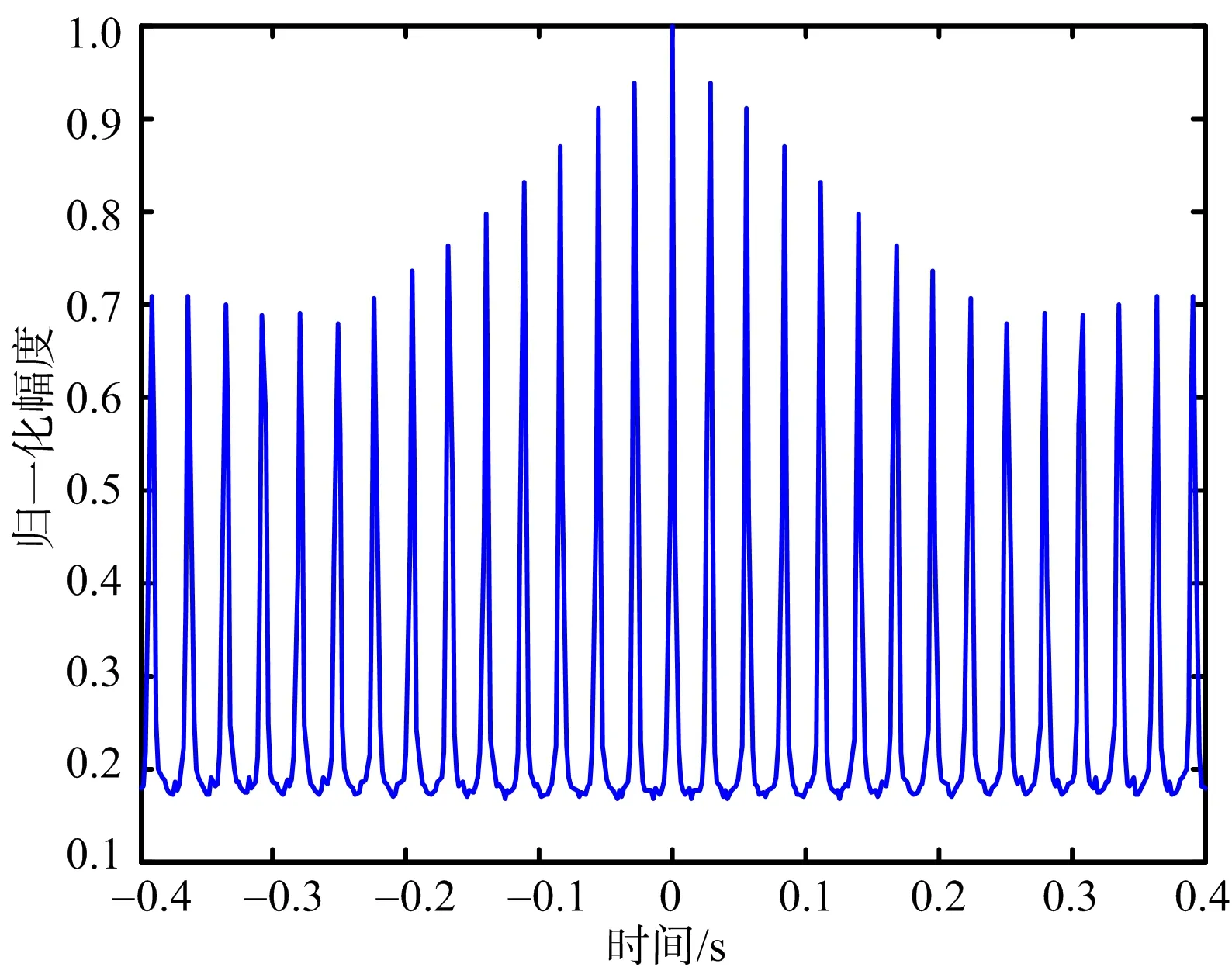
图13 分离后第238个距离单元信号自相关
6 结束语
本文从含有微动特征信息的螺旋桨飞机目标的雷达实测数据中,获得其二维逆合成孔径雷达(ISAR)图像,采用时频分析技术分离出目标主体成像和微动部件成像,实现机身回波和主旋翼回波的分离,并对微动信号作单独分析,更好地获得旋转部件的微动参数特征, 最后,通过仿真和实测数据验证了本文提出算法的有效性。
