智能网联汽车主动制动避撞算法联合仿真
2021-08-02林国庆韩龙飞刘俊超
林国庆,逯 超,韩龙飞,刘俊超
(长安大学,陕西 西安 710064)
0 引 言
智能网联汽车快速发展,主动避撞系统能够大幅度提高智能网联汽车的行车安全。交通事故不仅会造成直接的经济损失,还会造成人员伤亡,据统计,车辆追尾导致的碰撞占交通事故总量的30%~40%,因此,研究主动避撞系统的研究对智能网联汽车的发展具有非常重要的意义。
对危险进行准确合理的估计是智能网联汽车主动避撞系统中的一个核心问题[1-2]。同济大学刘瑞等人[3]结合碰撞时间TTC和车间时间THW衡量汽车运行风险时的优点,在自然驾驶数据的基础上,提出基于驾驶员避撞行为的行车风险状态分类方法,通过机器学习建立反映不同驾驶员行为、道路和环境特征的行车风险判断方法,为研究防碰撞预警算法和控制策略提供了新思路;Kondoh T等人[4]综合考虑TTC倒数与THW倒数,并提出使用TTC倒数与THW倒数的加权和来判断行车危险系数;Sengupta R等人[5]使用碰撞时间和碰撞距离作为纵向避撞系统决策指标,设计了用于判断前方相同车道是否存在碰撞风险的协同避撞系统;西安交通大学章军辉等人[6]建立了基于BP神经网络的闭环驾驶跟驰习惯模型,设计了激进、谨慎、新手3类典型驾驶群体,通过制动深度、期望的TTC倒数、应急反应时间来表征驾驶群体特性,实现了差异化预警;Balint A[7]对车辆制动时的追尾场景进行数学建模和分析,根据自车与目标车的相对速度进行危险状态估计,从而确定车辆的制动时刻以避免碰撞;李霖等人[8]基于真实交通工况下驾驶员的紧急制动行为特征,建立了基于碰撞时间倒数tiTTC和期望减速度areq的危险估计算法;袁伟等人[9]基于制动过程给出制动临界避撞距离,并以纵向行驶安全系数ξ和碰撞时间倒数TTC-1划分安全行驶区域;胡远志等人[10]按照车速划分不同的行驶工况,并设置不同的TTC阈值,有效提高了避撞系统的稳定性与安全性。
该文在已有的研究成果的基础上,综合考虑智能网联车辆的运动状态(速度、加速度等)、驾驶行为特征以及路面附着系数影响,提出一种自适应的TTC阈值计算方法。首先采用扩展卡尔曼滤波(EKF)对路面附着系数进行在线估计;其次,根据估计的路面附着系数以及不同的行驶状态计算得到不同的阈值:预警阈值TTCw、紧急制动阈值TTCe,并建立相应的控制策略;最后利用CarSim-Simulink联合仿真,结果表明,所提控制策略有效提高了智能网联汽车在不同车速和路面附着条件下的避撞性能表现。
1 路面附着系数估计模型
本节研究了基于扩展卡尔曼滤波算法的路面附着系数估计方法。建立车辆动力学方程,根据车辆状态对路面附着系数进行估计。
1.1 建立车辆动力学模型
为了兼顾模型的精度与问题的简化,建立三自由度车辆模型,即车辆纵向、侧向以及横摆运动。整车模型如图1所示,对应的车辆动力学方程见式(1)~式(3)。

图1 车辆动力学模型
(1)
(2)
(3)
式中,vx和vy分别为汽车纵向和侧向速度;r为横摆角速度;m为整车质量;a和b分别为汽车质心到前后轴的距离;Tf和Tr分别为汽车前后轴轮距;δ为前轮转角;Fxij和Fyij分别为轮胎纵向力和侧向力;Iz为车体绕Z轴的转动惯量。
1.2 轮胎模型
为了对路面附着系数进行估算,轮胎力的计算公式需要能简单明确地反映路面与轮胎的附着关系。因此,本节选取表达形式较为简单的Dugoff轮胎模型来求解轮胎力。
Dugoff轮胎模型公式,可写成如式(4)和式(5)所示的归一化形式。
(4)
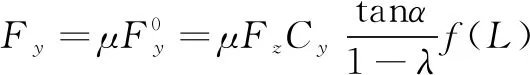
(5)
其中:
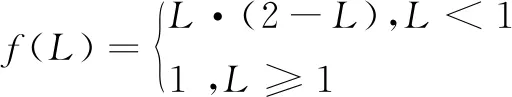
(6)
(7)
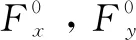
为了估计路面附着系数,各变量应易被传感器测得或估计得到。因此,根据上述轮胎模型可知,需要输入的参数有轮胎的垂向载荷,滑移率与轮胎侧偏角。
轮胎垂向载荷可由式(8)求得:
(8)
式中,h为汽车质心高度;l为前后轴间距。综合式(9)~式(12),可求出四个轮胎的滑移率:
(9)
(10)
(11)
(12)
式中,wij、λij、vij(i,j=fl,fr,rl,rr)分别为四个车轮的转速、滑移率、速度;vcog为汽车质心速度;β为质心侧偏角。轮胎侧偏角如式(13)所示:
(13)

1.3 基于EKF的路面附着系数估计
(1)根据上述模型,选取参数为:状态变量:x(t)=[μfl,μfr,μrl,μrr];输入变量:u(t)=[δ];测量变量:z(t)=[ax,ay,r]T。其中,ax、ay分别为纵向、侧向加速度,其与汽车纵、侧向速度的关系如式(8)所示:
(14)
(2)系统方程的建立。
结合状态参数估计思想,将车辆动力学模型整理为扩展卡尔曼滤波算法所需的状态方程和量测方程,如下式所示:
x(t+1)=F·x(t)+ω(t)
(15)
z(t)=h(x(t),u(t),v(t))
(16)
式中,ω(t),v(t)分别为过程噪声和量测噪声,根据参考文献[11-12],假设其为互不相关的高斯白噪声,矩阵F值为I4×4。
(3)模型线性化。
由上述方程可知,状态方程为线性,而量测方程为非线性,根据扩展卡尔曼滤波的思想,需通过泰勒展开将其线性化。由于文中研究不涉及弯道,前轮转角δ很小,可假设cosδ=1,sinδ=δ。对式(10)进行线性化得到雅克比矩阵为:
(17)
其中:
H(3,2)=
(4)仿真验证。
通过CarSim-Simulink联合仿真来验证上述路面附着系数估计算法的可行性。CarSim输出为前轮转角δ,纵、侧向车速vx、vy,纵、侧向加速度ax、ay,横摆角速度r以及四个车轮的转速wfl、wfr、wrf、wrr。从而通过Dugoff轮胎模型计算出四个车轮的归一化力,最终将上述参数输入到EKF参数估计器,可得到所求的路面附着系数。由图2、图3可知,该估计能够有效估计路面附着系数。

图2 附着系数为0.8的仿真结果
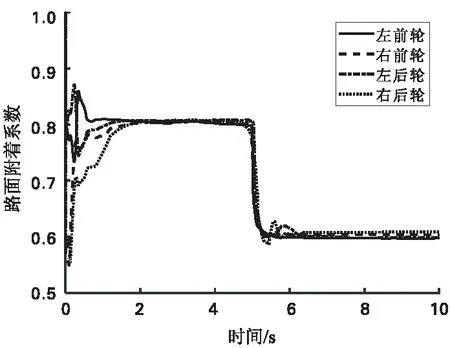
图3 对接路面的仿真结果
2 碰撞危险估计模型
基于传统TTC计算方法,充分利用车辆的运动状态(速度、加速度等),该文提出一种新的TTC计算方法。
2.1 预碰撞时间TTC的计算
根据两车运动状态,建立运动方程[13-14]:
(18)
式中,vr为自车与目标车的相对速度,ar为相对减速度,sr为相对距离,tTTC为预碰撞时间。
根据式(18)可得:
(19)
实验发现,式(19)在vr≤0 &ar<0和vr>0 &ar<0情况下计算的TTC数值互为相反数,因此该文采用的碰撞危险判定指标TTC为:
(20)
式中,μrg表示相对制动减速度。
2.2 制动阈值的计算与分析
两车之间的运动关系可得[15-18]:
(21)
式中,t1为驾驶员的反应时间,通常为0.3 s~1.0 s;t2为制动系统的延迟时间,通常为0.2 s~0.9 s;t3为制动控制系统的延迟时间,通常为0.1 s~0.3 s。awarning、amax分别为预警、全力制动时的制动减速度,制动减速度越大,危险等级越高。文献[8]的研究表明,汽车的制动减速度通常可达6.1 m/s2~10 m/s2,因此该文取awarning为0.6μg,μ可根据路面附着系数的估计得到。sw为预警临界制动距离,se为全力制动时的临界距离。综合式(20)、式(21)可得制动阈值TTCthreshold的计算模型:
(1)ar≠0时:
(22)
(2)ar=0时:
(23)
式中,TTCw表示预警阈值,TTCe表示全力制动时的阈值。
3 联合仿真
据统计,在全国高速公路交通事故中追尾碰撞事故数约占总事故数的33.4%[19-21],因此,研究主动避撞对提高车辆行驶安全性具有重要意义。该文参照最新版C-NCAP(2018版)对智能汽车AEB的测试方法,选取三种典型测试工况,使用CarSim-Simulink对所提控制算法及传统控制算法进行对比分析,每一种测试工况分别在高低两种不同的路面附着系数下(0.7、0.3)进行测试。测试时,当自车与目标车发生碰撞(相对距离为0)时,在Simulink中设置停止仿真,测试结果主要记录了TTC、自车速度、相对距离以及制动减速度的时序图。
3.1 前车匀速慢行工况(μ=0.3)
实验结果如图4所示,在附着系数为0.3的路面上,两车相对距离为50 m,主车速度45 km/h,前车速度为20 km/h。传统避撞算法(指路面附着系数为定值的算法)与文中所提算法具有较大的差异。文中算法的TTC起作用时间为2.0 s,制动时两车之间的距离为9.68 m,最终两车之间的最小距离为1.25 m。传统算法的TTC起作用时间为1.0 s,两者相差约1 s,开始制动时两车之间的距离为6.35 m。传统算法由于制动开始时刻过晚而未能成功避撞,在7.4 s时仿真停止,碰撞速度为32 km/h。

图4 前车匀速慢行工况
3.2 前车减速行驶工况(μ=0.7)
实验时,两车相距12 m,开始时两车速度均为50 km/h。实验结果如图5所示,仿真运行到5.24 s时,文中算法开始起作用,此时TTC阈值为1.87 s,两车相距8.22 m,汽车进行紧急制动,两车最小距离为1.8 m,成功避撞;5.43 s时,传统算法的TTC为1.4 s,此时两车相距5.75 m,由于制动时间过晚,在7.25 s时两车发生碰撞,仿真停止,碰撞速度约为10 km/h。
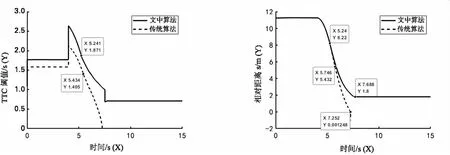
图5 前车减速行驶工况
3.3 路面突变工况
汽车制动时,路面附着发生突变主要分为两种:一是制动前路面发生突变,二是制动时路面发生突变,针对第二种情况,对文中算法进行仿真验证。为了保证汽车在制动过程中路面发生突变(μ=0.8变为0.6),在CarSim中设置对接路面,并设置0 m~46 m为μ=0.8的路面,之后为μ=0.6的路面。测试时,前车静止,两车相距50 m,道路长度为100 m,自车以30 km/h的速度向前行驶,仿真结果如图6所示。5 s时,两车相距约7.5 m,自车行驶了42.5 m,此时路面附着未发生突变(设置在45 m处路面附着开始突变),μ=0.8,自车以最大减速度0.8 g开始制动。5.5 s时,两车相距约4.3 m,自车行驶了46.7 m,此时路面附着发生突变(μ由0.8变为0.6),制动减速度由0.8 g变为0.6 g,最终两车的相对距离为2.4 m,成功避撞,验证了文中算法在路面附着突变的情况下的有效性。
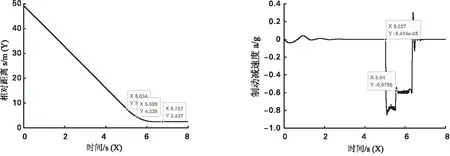
图6 路面突变工况仿真结果
3.4 自适应主动制动避撞算法分析
在CarSim中设置前车以20 km/h的速度匀速慢行,自车以40 km/h的速度匀速行驶,两车相距50 m,分别在路面附着系数μ=0.3、μ=0.5、μ=0.7以及μ=0.8的路面上对文中所提自适应算法进行测试,结果如图7所示。

图7 不同附着系数下仿真结果
由TTC的时序图可知,文中算法的TTC可以较好地跟随路面附着系数的变化,即使在低路面附着系数(μ=0.3)上,也能与前车保持约0.7 m距离,在μ=0.5、μ=0.7以及μ=0.8的路面上,两车之间的距离保持在1.8 m左右,这比较符合预期的结果,充分证明了文中算法的有效性。
4 结束语
以智能网联汽车为载体,该文提出能够跟随路面和相对速度变化的主动制动避撞算法,通过CarSim-Simulink联合仿真,在不同附着系数下验证了算法的有效性,主要得出以下结论:①所设计的TTC及TTC阈值能够根据路面附着系数和相对速度的变化做出自适应调节(特别是在低附着系数的路面上),优化了制动系统的介入时机;②避撞控制算法能够根据车辆运动状态做出合理的危险判断,采取相应的制动措施,并与前车保持合理的距离,符合大多数驾驶员的制动行为。
需要说明的是,①该文仅仅是在视野良好并已经确知了前车距离和相对速度的前提下研究了主动制动避撞算法,在视野受限的情况下存在一定的风险,后续将融合V2X技术,对实现智能网联汽车的主动避撞进一步研究;②该文仅通过仿真验证对几个典型场景进行了测试,而未进行实车实验,下一步将进一步优化算法并进行实车实验,提高算法的鲁棒性。
