伙伴学习，共同生长——核心素养下数学数形结合思想的渗透

江苏省张家港市南丰小学 赵卫军

一、核心素养下数学数形结合思想渗透的背景分析

小学阶段学生的数学思维能力较弱，对抽象问题的理解和思考能力相对较弱。比如，面对概念性的问题，学生很难理解，以至于出现一些教师和家长认为比较低级的错误。究其根源，还是由于学生缺乏数学思维，并不能将数量关系与图形关系有机地结合起来，在一定程度上导致了心理上学习难度的加剧。

教师在日常教学和练习测试过程中，经常会遇到一些问题，比如：

第一个问题很简单，大多数的学生都会正确解答；而第二个问题则会有如100-23+30=47的错误回答。产生错误的根源就在于学生并没有充分理解组合算式的含义，只是简单地做了一个“搬运”的工作。追根溯源，一方面，学生缺少一个整体的数学思维；另一方面，教师在讲解问题的过程中缺乏对数形结合思想的渗透，只是从算式的本身进行知识的讲解，并没有考虑到当前低年级学生数学思维的特点，从而导致学生只会死板地套用教师的方法，而跳过了自主思考、探索的过程。

低年级简单的加减法混合运算尚且如此，那么随着年级的提升，学生接触到的数学知识越来越复杂，数学思想的渗透以及学生数学思维的培养便越来越重要。因此，基于数学学科核心素养的新型数学课堂的创建，要为学生提供更加明确的数学思想的引领以及合作学习的机会，真正地发挥出数形结合等数学思想对学生数学学习的作用，同时借助多样化的数学活动过程，培养学生的自主学习意识。

二、核心素养下数学数形结合思想渗透的策略分析

1.以形助数

借助“形”的直观性特征，将数量关系通过“形”展现出来，能够从根本上降低学生理解数量关系的难度，进而有效提升学生的课堂学习综合效果。

例如，23+30=53，100-53=47，将这两组算式进行组合，成为一个正确的算式。如果我们借助图形之间的关系将数量关系表示出来，那么学生很容易就能理解。在引导过程中，教师可以通过问题引导的方式进行思路的引领，让学生一步步地明确思路。例如：

生：（23+30）。

师：非常棒，那么接下来谁能够告诉老师，这两个算式的组合是什么？

……

通过简单地引入图形，让学生更加明确简单的组合算式之间的数量关系。有前期知识做铺垫，学生缺少的只是一个思维的引领，借助图形，教师可以少费口舌，而且非常生动形象，再配合动态的视频讲解，学生的思路就会更加明确。

此外，在行程问题和追及问题中，数形结合思想也是非常重要的，行程问题是小学数学非常重要的一部分内容，也是很多学生觉得非常难学的内容，如下案例所示：

结合学生当前掌握的数学知识现状，如果单纯地从数量关系考虑两地之间的距离，通过计算两车速度、行驶时间等，学生很容易被“第二次”相遇这一数据误导，进行错误的计算：（240+250）×9÷2=2205（km），忽略了第二次相遇整个行程其实是上海到北京距离的3倍。那么用数形结合的方式，两车之间的行程以及上海到北京之间的距离就能够非常清楚地展现出来，如图1所示：

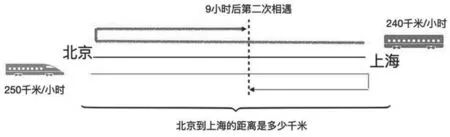
图1

由图1可知，9个小时后两列车第二次相遇，其实总共的行程是上海到北京距离的3倍，因此正确的答案应该是（240+250）×9÷3=1470（km）。由此可见，将行程问题与数形结合思想相结合，不仅能够降低题目难度，而且能够提高学生解题的正确率。

2.以数解形

在数学学习与研究过程中，“形”虽然能直白地表示出数学关系的含义，但有时缺少一定的精确性。因此，以数解形，能够让学生对数学知识的理解精确化，有效地完善学生的数学思维，将内容具体化。

例如，在垂线与平行线的教学过程中，教师一般从新课标的要求入手，让学生先认知垂直、平行、相交等基本的概念，最终通过平行与垂直等概念解决实际问题。教师可以从不同层次的教学目标入手，结合多媒体教学的便利性，从生活中一些常见的事物和现象入手，将数学课堂与实际生活有机结合，加深学生对垂直与平行的关系的理解。那么在具体的课堂实践操作过程中，教师创设翻转课堂教学模式，引导学生自主探究两条直线之间的位置关系。

师：同学们，假如在一张纸上画两条直线，那么这两条直线之间存在什么样的位置关系？接下来同桌为一组，看看谁能够画出最多的位置关系。

（同学们两两一组，结合先前学过的知识，在练习本上画出了很多种直线位置关系，如图2）

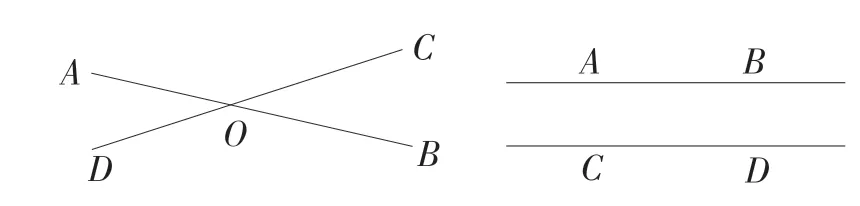
图2

学生画出了上述两种情况，由此可见，学生已经基本掌握了两条直线的位置关系。教师结合小组讨论的情况，让每个小组分享了自己的讨论结果，根据学生分享的结果，教师将图形赋予“数”的意义，让学生能够更加明确两条直线的位置关系。

师：同学们总结的位置关系非常正确，那么在这些直线的位置关系中，你们有没有发现什么共同点呢？

生：第一类两条直线是没有交点的，第二类是有一个交点的……

教师结合学生的探究和分享的问题引出具体的数量关系，然后以表格的方式进行总结（见表1）：

表1

在学生明确了两种位置关系的基础上，教师引出另外一种关系（如图3）：

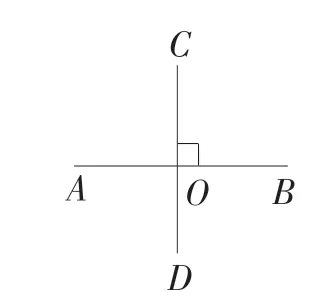
图3

师：同学们请看这两条直线，它们的位置关系比较特殊，这种关系叫什么呢？

……

此种方式下，学生能够更加清晰两条直线之间的位置关系，将形与数有效结合起来，加深学生的学习印象，为后期利用数形结合思想解决问题做好充分的准备。

3.数形结合

数形结合是解决问题的过程中经常采用的一种方法，数形结合将困难的问题简单化，将抽象的问题生动化，让学生能够更加清楚地了解数学问题的始末。在数形结合应用过程中，最为典型的就是解决鸡兔同笼问题。

案例：笼子里一共有若干只鸡和兔子，从上面数有8个头，从下面数有26条腿，那么鸡和兔子各有几只？（教师将学生分为了几个小组，鼓励他们用自己现有的知识去解决鸡兔同笼问题）

生（小组一）：我们用的是列表法。（见表2）

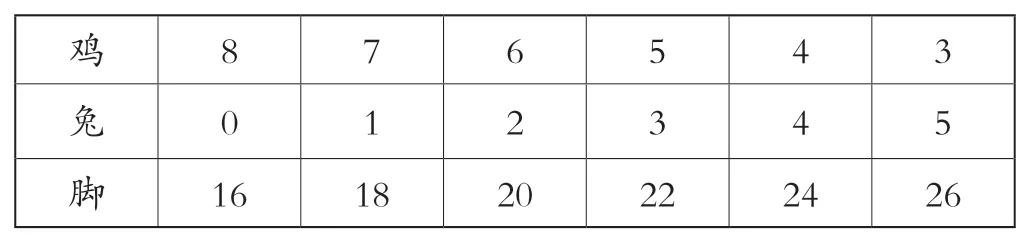
表2

（学生共同研究、讨论，通过列表法得出鸡有3只，兔子有5只）

生（小组二）：我们采用的是画图法。（见图4）

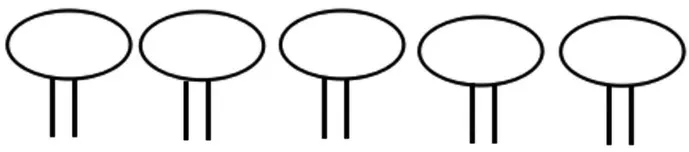
图4

8个头代表有8个动物，那么假设所有的都是鸡，我们先把鸡画好，这样一共有8×2=16条腿，差26-16=10条腿，这样就需要把5只鸡的腿补成4条，而补成4条腿的鸡就变成了兔子，所以鸡的数量应该是8-5=3只，兔子的数量就是5只。

学生通过小组合作的方式，结合列表法、作图法解决鸡兔同笼问题，借助推理将两者之间的数量关系清晰地表述出来，从而得出正确的结果。借助数形结合避免了学生数学思维能力较弱带来的解题困扰；通过简单的引入图形，帮助学生更加明了题目中的数量关系，再加上前期课堂知识铺垫，以及教师思维的引领，既不用教师多费口舌，还能形象地展现题目内容，使学生思路更加明确。

总之，通过数与形之间相互协助的关系，可以建立起学生最初的学习数学的思维，改变传统理念下数学课堂本末倒置的局面，减少甚至杜绝教师一味关注教学结果的弊端，引导教师逐渐重视教学过程。在顺应学生学习特征，构建高效课堂的同时为今后的数学教学活动奠定坚实的基础。