基于CFD方法的熔盐储罐预热分析

2021-07-31王鼎肖虎陈宇轩岳松张燕平

综合智慧能源 2021年7期

王鼎，肖虎，陈宇轩，岳松，张燕平*

（1.华中科技大学能源与动力工程学院，武汉 430074；2.湖北省电力勘探设计院有限公司，武汉 430040）

0 引言

在碳中和背景下，构建以可再生能源为主体的新型电力系统成为电力系统转型的方向，而储能技术是重要的支撑技术。太阳能光热发电（CSP）技术是一种清洁、高效的发电方式，具有能量密度高、发电平稳、电网兼容性好等优点［1］。与光伏发电相比，CSP 技术最大的优势在于可增加储热系统，使系统在夜间或气候骤变等光照不足的时候，仍能保证电能的持续输出，较好地扭转了光热发电不能稳定持续的劣势，使太阳能的大规模利用成为可能。

目前，世界上大部分运行或在建的光热电站都配备了储热系统［2］。常见的储热系统主要包括单罐和双罐2 种类型，储热介质包括水、空气、熔盐等。目前，商业化光热电站主要采用熔盐作为储热介质并采用双罐储热系统［3］。熔盐储罐作为储热系统中的关键设备，不仅决定了系统的蓄热能力，而且对光热电站的安全运行也有重要影响。2016年10月，美国新月沙丘电站发生的熔盐储罐泄漏事故导致该电站暂时停运，预计经济损失在400 万美元以上［4］。因此，对熔盐储罐的热学性能进行进一步研究具有重要意义。

近年来，国内外学者基于数值模拟对熔盐储罐的散热损失和温度分布进行了大量理论研究。Schulte 等［5］利用计算流体动力学（CFD）方法研究了880 MW 储热系统的热损失，发现储罐底板与侧壁边沿的热损失较高。Zaversky 等［6］基于Modelica 建模语言建立了熔盐罐的瞬态热损失模型，发现罐壁与熔盐间的对流及辐射散热是热损失的主要因素。顾清之等［7］通过FLUENT 计算获得了熔盐储罐在冷却过程中的散热量及熔盐温度下降规律。崔凯平等［8］通过数值模拟证明了利用再循环管道和分配环进行扰动可以有效改善熔盐储罐热分层现象。此外，不少学者对熔盐储罐的运行进行了工程试验研究。Pacheco 等［9］计算得到美国Solar Two 光热电站热罐（565 ℃）和冷罐（290 ℃）的散热损失分别为（102±21.0）kW 和（44±6.6）kW。Zhang 等［10］建立一种以新型熔盐为储热介质的工程储热系统，试验研究了冷却过程中罐内熔盐及储罐基础的温度分布。

事实上，熔盐储罐的运行还面临一些实际工程问题。在电站投入使用初期或长时间停机后再次投运前，必须对储罐进行预热以减小充盐时热冲击造成的影响，然而由于储罐体积巨大，实际预热过程常常超过200 h，工期成本高。时华等［11］利用定温热空气对小型熔盐储罐进行预热，获得了罐壁不同位置的升温规律；韩伟等［12］提出一种熔盐储罐精细化设计方法，基于数值模拟研究了预热时罐体的温差和温升。

储罐的预热对于光热电站的安全稳定运行有重要意义，但目前这方面的研究较少，对影响预热过程的因素研究不够充分。本文以某实际光热电站中的熔盐储罐为研究对象，采用等阶梯式升温的预热方案，基于CFD 法对预热过程中储罐的温度分布进行数值模拟，探究了预热气体喷射角和储罐尺寸对预热过程的影响，以期为工程上熔盐储罐预热方案的设计与选择提供参考。

1 模型及方法

1.1 熔盐储罐物理模型

某实际光热电站的熔盐储罐罐体直径为25 000 mm，高12 500 mm，几何模型如图1a 所示。罐体由罐顶、侧壁和罐底3个部分组成，其中储罐侧壁由厚度不同的环形钢板焊接而成，越靠近罐底的钢板厚度越大，自底向上钢板厚度分别为30，26，20，16，12 mm。罐壁外侧包裹了硅酸铝纤维作为保温层，厚度为500 mm。储罐基础主要采用砾砂、页岩陶粒、混凝土等多层材料进行铺设，可以有效减少储罐底部的散热量。预热气体进、出口管的直径分别为500 mm 和600 mm，两者的位置如图1b 所示：进口管位于储罐顶部，喷射方向与竖直方向成45°，周向角度与圆心连线夹角成40°。储罐预热是通过预热气体进口管喷射高温气体在罐内形成环流来实现对罐体的加热。

图1 储罐模型示意Fig.1 Schematic storage tank model

1.2 数学模型

高温预热气加热罐体时，其传递的总热量Qtot主要包括储罐壁面吸收的热量Qtank、储罐内气体的内能变化量Qair以及储罐与外部环境的换热量Qw，即

式中：Qin为预热气体进口能量；Qout为预热气体出口能量；qm为预热气体进口的质量流量；hin为进口预热气体的焓；hout为出口预热气体的焓。

式中：mtank为罐体质量；ctank为罐体比热容；ttank为罐体平均温度；t为预热时间；mair为罐内气体质量；cair为罐内气体比热容；tair为罐内气体平均温度。

式（1）中的Qw包括3个部分，

式中：Qb为通过罐底的换热量；Qs为通过罐侧壁的换热量；Qt为通过罐顶的换热量。

罐体的最大温差Δttank可以在一定程度上反映加热过程的均匀性，

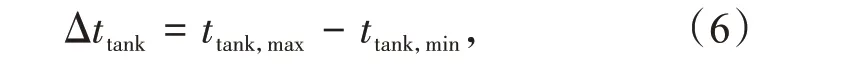
式中：ttank，max，ttank，min为罐体的最高和最低温度。

预热气体在罐体中的流动和换热满足质量、动量和能量守恒定律，相应的控制方程为［13］

式中：ρ为流体密度；∇为哈密顿算子；ν为流体的速度矢量；p为流体静压；tij为微元表面上的黏性应力张量；g为重力加速度；E为单位质量流体的能量；k为流体的导热率；T为流体温度。

通过计算流体动力学软件FLUENT，对储罐预热过程进行瞬态热模拟，预热气体的热物性与空气相似，参见文献［14］，储罐其他材料的热物性参数见表1，其中罐体材料的比热容、罐体材料和保温材料的导热率均随温度变化，故拟合为关于温度的函数关系式输入FLUENT。在模型设置中，湍流模型采用Standardk-ε模型，储罐高温壁面间的辐射换热采用表面辐射（S2S）模型。

表1 罐体和保温材料的物理性Tab.1 Properties of tank and insulation materials

进口设质量流量为进口边界条件，出口设压力为出口边界条件；保温层外壁设为等温边界，与环境温度相同，为0 ℃。基于有限体积法求解控制方程，通过SIMPLE 算法求解压力-速度耦合场，压力离散格式选用Standard。在软件ICEM 中，利用结构化网格、非结构化网格相结合的方式对储罐进行网格划分，如图2 所示。经过网格数量无关性验证和时间步长独立性验证，确定网格数为89 万，时间步长选择15 s，这样可兼顾计算精度和时间成本。

图2 储罐网格划分Fig.2 Grid division of a storage tank

1.3 预热方案

本文采用等阶梯式升温预热方案，即控制预热气体进口温度呈等阶梯式上升加热罐体。定义预热气体与罐体之间的最大温差为温度端差Δt。以Δt=150 ℃的预热方案为例，储罐初始温度为0 ℃，预热开始时通入进口的预热气体温度为150 ℃；每当监测罐体平均温度升高50 ℃，控制预热气体进口温度提高50 ℃，使得预热气体与罐体之间的温度端差保持在150 ℃，以此类推，直到罐体平均温度达到目标预热温度380 ℃。

2 模型验证

采用某光热电站中熔盐储罐预热的试验数据来验证本文数值模型的有效性。数值模拟采用了与现场相同的阶梯式升温预热方案，具体应用的进风条件见表2。

表2 现场实际预热方案Tab.2 Preheating plan on site

实际过程与模拟过程中罐体平均温度的对比见表3。从表3中可以看出，模拟过程和实际过程中罐体的平均温度在前100 h 的相对误差较大，随着加热的进行，罐体温度不断上升，相对误差逐渐减小至3.68%。考虑到实际工程条件和模拟计算的理想条件之间的差异，本文的储罐预热计算模型具有较好的可靠性。

表3 实际过程与模拟过程中各时间点罐体的平均温度Tab.3 Actual and simulated average temperatures of the tank at each time point

3 结果与分析

3.1 储罐温升与温度分布

3.1.1 储罐温升

图3 给出了预热气体质量流量为2.7 kg/s 且温度端差为150 ℃时预热气体进口温度和罐体平均温度随时间变化的曲线。每个阶梯加热区间内，预热气体进口温度保持不变，罐体温度上升却越来越慢，这是因为预热气体与罐壁之间的温差越来越小，削弱了罐内的对流换热。随着预热过程的进行，罐体整体温升也越来越慢。一方面，罐壁温度的增加增大了其与保温层外壁的温差，导致了更多的散热量；另一方面，罐体的导热系数随着温度的增加而减小，但比热容却增加，因此上升相同温度需要吸收更多热量。

图3 预热气体温度和罐体平均温度随时间的变化Fig. 3 Preheating gas temperature and tank average temperature varying with time

图4给出了预热过程中罐体最大温差和温升速率随时间的变化趋势。预热刚开始时，最大温差急剧增加，到达最大值后，整体呈下降趋势，只有在提高预热气体温度时最大温差会有突然的上升，但幅度越来越小。这说明随着预热的进行，储罐内部的温度分布越来越均匀。罐体温升速率表征单位时间内罐体温度的增加量，直接反映了加热的快慢。预热过程中，罐体温升速率从超过10 ℃/h 逐渐降低到小于1 ℃/h，温度升高50 ℃所花的时间也逐渐增加。这表明预热后期的加热效果比较差。考虑到高温条件下壁面温差对储罐预热安全的影响更显著，因此不得不接受更苛刻的预热要求。在保证安全的前提下，可以采用增加温度端差或预热气体质量流量的方式来提高升温速率。

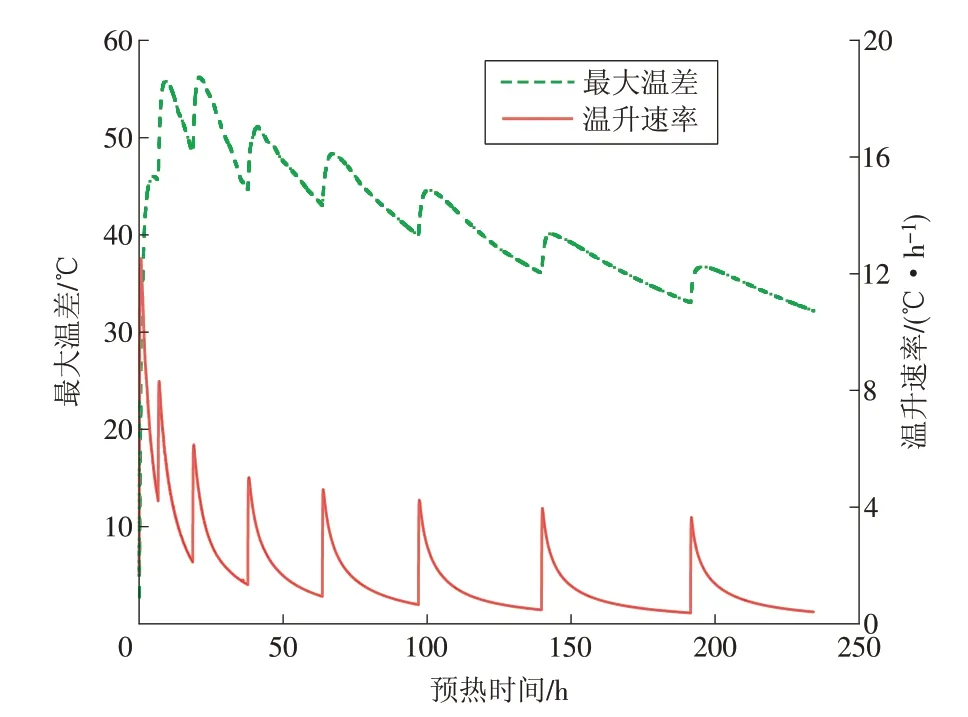
图4 罐体最大温差和罐体温升速率随时间的变化Fig. 4 Maximum temperature difference and temperature rise rate of the tank varying with time

3.1.2 储罐的温度分布

图5 显示了预热20 h 后，罐内气体和罐壁的温度分布。由图5a可以看出，预热初始阶段的保温层温度还很低，罐内气体的温度分布不均匀，上部温度高，下部温度低，分层明显。由于预热气体进口喷射方向与圆心连线成一定夹角，因此罐内气体的旋流明显，边缘温度高、中心温度低。由图5b可知，罐体侧壁和顶部边沿出现高温区域，这是因为喷射进入的高温气体首先沿着进口方向加热相邻侧壁，然后在罐内沿着罐壁旋流，因此罐顶越靠近边缘处温度越高，而罐底温度较低。在预热初始阶段，罐内高温气体旋流上升，冷空气聚集在罐底附近，并且地基材料比保温材料的导热系数大，导致罐底加热效果较差。罐体底板与侧壁交界的边缘处温度最低，这一区域远离预热气体进、出口，气体流动缓慢，无法得到有效加热。

图5 储罐的温度分布Fig.5 Temperature distribution of storage tank

3.2 预热气体喷射角对预热过程的影响

由图1 可知，预热气体进口的喷射角可以分为竖直方向和周向2 个方向，分别定义为喷射方向的竖直角和周向角。这2个角度影响高温气体在罐内的旋流，需要探究其对预热过程的影响。

表4 给出了预热气体质量流量为2.7 kg/s、温度端差为250 ℃、周向角为40°时，不同竖直角下罐体平均温度达到预定温度所需时间。随着竖直角度的增加，罐体温度升高到380 ℃时所需时间逐渐增加：该时长从竖直角为35°时的66.5 h 增加到55°时的73.1 h，时长约增加10%。这是因为竖直方向角度越小，罐下部的冷气体扰动越充分，使得罐内冷热气流混合更均匀，有利于罐体预热的进行。

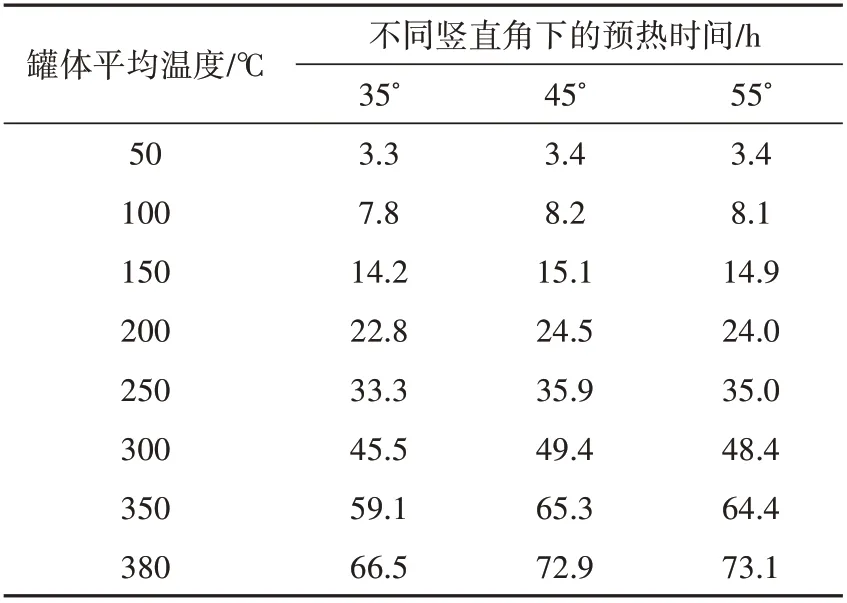
表4 不同竖直角下罐体预热所需时间Tab.4 Time required for tank preheating under different vertical angles

图6显示了不同喷射竖直角下罐体最大温差和温升速率随时间的变化。3 种竖直角下，罐体最大温差和温升速率的变化趋势基本一致，数值区分度很小：预热过程中罐体最大温差整体呈现先急剧增大然后缓慢衰减的趋势，温升速率整体也呈衰减趋势；预热时间超过10 h 后，温升速率低于10 ℃/h，但3 种竖直角下最大温差的峰值均已超过80 ℃，会导致罐体热应力增大。由此说明，在数值模拟中采用较大的温度端差虽然可以明显减少预热时间，但可能存在一定的安全风险，因此实际工程中需要采用合适的温度端差值。

图6 不同竖直角下罐体最大温差/温升速率随时间的变化Fig.6 Maximum temperature difference and temperature rise rate of the tank varying with time under different vertical angles

以45°竖直角为例，不同喷射周向角下罐体平均温度达到预定温度所需时间不同，见表5。随着周向角度的增加，罐体温度升高到380 ℃所需时间逐渐减少：预热时间从30°时的73.8 h 减少到50°时的69.7 h，缩短了约6%。这是因为周向角度越大，高温气体沿着罐壁的旋流效果越好，对罐内的对流换热起到一定强化作用。不同喷射周向角下罐体最大温差和温升速率的数值区分度很小，因此不再赘述。

表5 不同周向角下罐体预热所需时间Tab.5 Time required for tank preheating under different circumferential angles

3.3 储罐尺寸对预热过程的影响

熔盐储罐的蓄热能力与储罐尺寸成正相关。系统要求的蓄热能力越大，所需熔盐储罐的内径也就越大。为了探究储罐尺寸对预热过程的影响，本文也对同一厂家为不同装机的光热电站设计的不同储热时长、各种尺寸的储罐进行模拟研究，详细设计参数见表6。

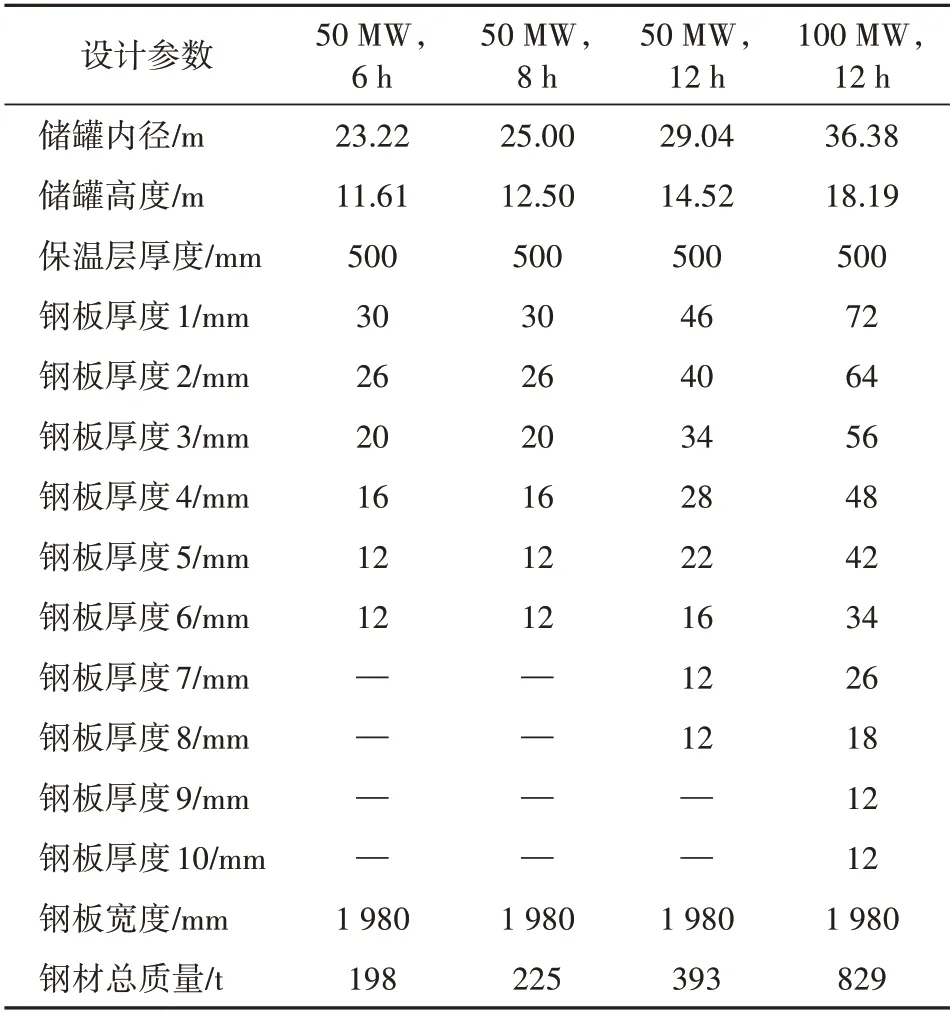
表6 储罐尺寸Tab.6 Size of the tank

图7 不同内径下罐体温度随时间的变化Fig.7 Changes of tank temperature with time under different inner diameters

该模型定性地说明了不同尺寸储罐建模的合理性。随着储罐内径增加，罐体温度升高到380 ℃时所需时间大幅提升，从23.22 m 时的63.1 h 增加到36.38 m 时的303.3 h，内径增长约57%，预热时间增长约380%。这是因为随着储罐内径的增加，储罐容积成立方增加，承载的熔盐量愈来愈大；另外，考虑储罐的安全稳定运行，储罐侧壁的钢板厚度也在增加，罐体升温所需加热的金属质量大幅增加，罐体升温至目标温度的时间也大大增长。由于模拟均采用单个进、出口的方案，若想减小大尺寸储罐的预热周期，可以增加预热气体进口的数量。

图8 显示了预热气体质量流量为3.6 kg/s 且温度端差为200 ℃时，不同尺寸罐体最大温差随时间的变化趋势。比较3 条曲线，发现随着储罐尺寸的增加，罐体最大温差逐渐减小。当储罐内径为36.38 m 时，最大温差约48 ℃，比储罐内径为23.22 m 时的最大温差降低了约10 ℃。且在预热后期，最大尺寸的储罐最大温差基本维持在10 ℃左右，说明在相同预热气体进出口条件下，大尺寸储罐预热过程更为安全。