基于粒子群优化算法的社交网络结构平衡的实现
2021-07-30李赵兴刘琼海
李赵兴,陈 莉,刘琼海
(1.榆林学院信息工程学院,陕西西安 719000;2.西北大学信息技术学院,陕西西安 710071;3.黄委晋陕蒙监督局,陕西榆林 719000)
社交网络的兴起改变了人们的日常生活方式,人们可以借助社交媒体方便地表达自己的观点和情感,并通过社交平台建立广泛的社交关系。对社交网络展开相关研究,不仅可以挖掘社交网络中的人群结构特征,还可以分析和预测网络上的信息传播流向以及信息传播可能造成的后果,因此,对社交网络的研究具有重要的理论研究意义和实际应用价值[1]。
研究社交网络特性的一种有效途径是将社交网络建模成由节点和边组成的复杂网络形式,其中节点表示网络的组成成员,边表示成员之间的社交关系,通过分析和挖掘复杂网络的基本特性来达到认知社交网络以及辅助决策支持的目的。由于社交关系通常存在友好和敌对两种情况,因此很多社交网络都被建模成由正边和负边表示的复杂符号网络形式,其中正边表示友好关系,负边表示敌对关系。复杂网络具有很多重要的特征[2-3],例如小世界特性、无标度特性等。近年来,复杂网络又一重要特性即社区结构特性[4-5],被学者发现。
文中针对社交网络的平衡结构问题[6-7]展开了研究,将平衡结构问题建模为能量最小化优化问题,提出了一种高效的离散粒子群优化算法,用以解决建模的优化问题。结合社交网络的拓扑结构信息,文中重新定义了粒子的离散表示,构建了基于离散表示的粒子更新方程。与现有的网络结构平衡求解方法相比,提出的算法不仅可以实现网络的结构平衡,还可以挖掘网络的社团结构,而且可以自动得到最佳的社团结构。所提算法的有效性在真实符号网络数据上得到了验证。
1 网络结构平衡
结构平衡是包括社会网络在内的网络研究的重要内容。对于图1 所示的3 个节点构成的网络,根据结构平衡理论,图1(a)和图1(b)被认为是平衡结构,而图1(c)和图1(d)是非平衡结构。图中的“+”代表喜欢、友好等“正”关系,而“-”则表示不喜欢、敌对等“负”关系。
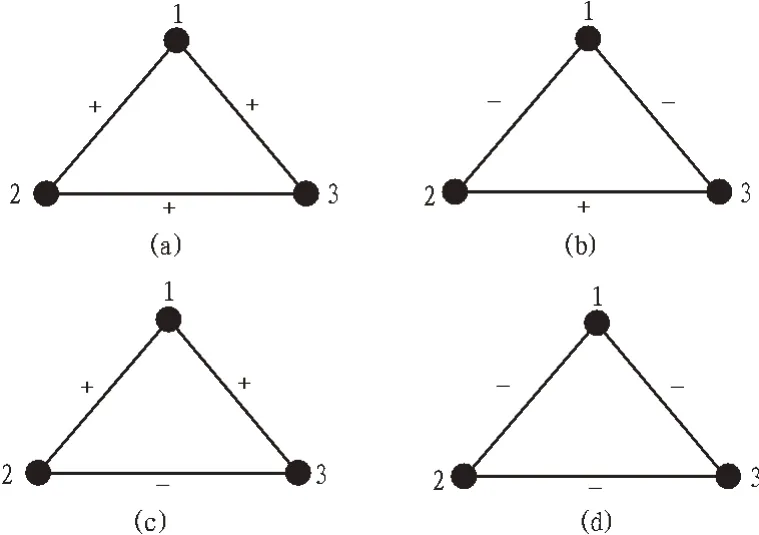
图1 平衡结构示意图
结构平衡定义和基本理论已经被系统研究,其在社会心理学、国际关系以及互联网络等领域受到广泛关注。
对于任意一个复杂网络,若该网络的节点可以分成X 和Y 两个子集,且X 和Y 满足图2 所示的关系,则称该网络是结构平衡的[8]。
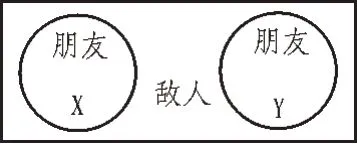
图2 网络结构平衡条件
大量研究表明,上述的结构平衡条件过于严格,多数网络可以被分成多于两个的子集,且这些子集也可以满足X 和Y 的特性。对于现实中的社交网络,很少网络是结构平衡的,大多数网络需要改变网络中某些边的属性或者增加/减少网络的边数来实现结构平衡[9]。
2 粒子群优化算法
粒子群算法[10]模仿鸟类觅食的行为,通过对比周围鸟类的飞行速度来不断调整自己的飞行状态,从而得到最优路径[11]。
如果一个粒子群有m个粒子,粒子被抽象为没有质量和体积的微粒,第i个粒子在m维空间中的位置可以用向量表示,飞行速度表示为向量=(vi1,vi2,…,vim),则每个粒子更新自身状态的规则可以表示为:
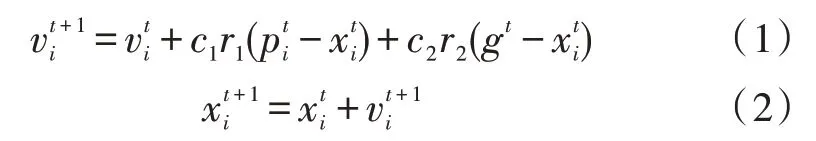
每个粒子都有一个被优化函数决定的适应值,并且知道目前为止发现的最好位置=(xpi1,xpi2,…,xpim),即通常说的粒子个体引导者,即该粒子可以找到的最佳飞行方向;此外,每个粒子还知道周围最优粒子发现的最好位置=(xgi1,xgi2,…,xgim)。c1和c2均为加速度系数,r1和r2为服从均匀分布U(0,1)的随机数。粒子群优化是不断优化的算法,每个粒子根据式(1)、式(2)不断调整自己的飞行轨迹,以得到最优解逼近[12-13]。
3 基于粒子群优化的网络结构平衡
3.1 算法框架
文中提出的离散粒子群优化算法通过最小化网络能量函数来寻找网络中存在的不平衡边,然后改变不平衡边从而实现网络的结构平衡。提出算法的工作流程图,如图3 所示。

图3 算法工作流程图
3.2 粒子适应度函数
文中利用适应度函数来度量粒子对生存环境的活跃度,并用适应度函数来评价社交网络的平衡度。
文献[14]提出了一种度量网络平衡程度的能量函数H(s),其定义如下:

其中,aij∈{±1}是网络邻接矩阵的元素,si和sj分别表示节点i和节点j的符号。若节点i和节点j属于朋友,则si·sj=1,否则si·sj=-1。
若一个网络是结构平衡的,则其对应的能量函数值H(s)=0,且能量函数越小代表该网络越趋近结构平衡。文中利用粒子群优化算法来最小化能量函数,从而寻找具有最小能量函数值时对应的网络社区结构,继而通过改变非平衡的边使网络结构达到平衡。
3.3 粒子的表示
首先对复杂网络中的点进行编码,然后采用粒子群优化算法对编码的网络进行优化。由于提出的算法要最小化H(s),因此针对结构平衡问题,文中采用基于字符串的方式对网络节点进行编码,这种编码可以很好地对网络节点进行描述,而且解密也比较简单。文中针对网络进行了粒子的重新编码,如图4 所示。
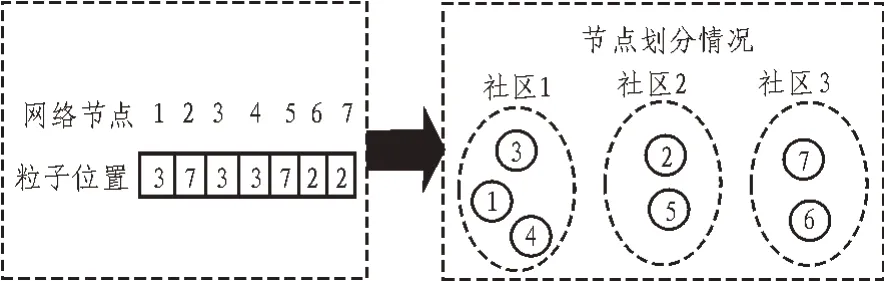
图4 粒子表示示意图
由图4 可知,粒子的位置采用整数排序,网络中的每一个节点都采用一位数字来标记,并按照标记号进行社区分类。在进行分类时,具有相同标记号的网络节点会被分配到同一个社区中。通过这样的编码,在网络划分时,会按照网络标记号自动分配成多个社区。
在进行解码时,若节点i和节点j属于同一个社区,则si·sj=1,若节点i和节点j属于不同的社区,则si·sj=-1。
3.4 粒子的状态更新规则
从粒子的表示方式可以看出,粒子的位置是整数编码的,因此传统的粒子状态更新方程(1)和(2)已经不再适用文中问题的求解。将粒子群优化算法应用在社交网络平衡中,并且重新定义粒子的状态更新方程,如下:
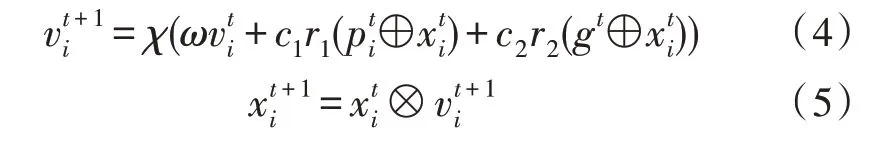
其中,ω为惯性权值常数,符号⊕表示异或操作。
函数χ(y)是一个压缩系数,其作用是确保PSO算法的收敛性,需将其转换为0 到1 之间的数,该压缩系数与位置向量根据式(4)操作。函数ζ(y)定义为:

式(5)中的⊗操作是粒子实时状态变化,符号异操作和或操作可以得到不同的粒子状态,该异或操作的使用会影响算法识别社区的能力,同时也会影响该算法的收敛速度。
针对一个复杂网络,一般两个节点在同一个社区的可能性小,而两个节点不在同一个社团的几率较大,针对该问题,文中定义的⊗操作如下:
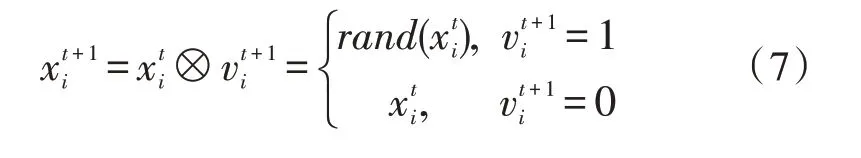
4 实验测试与分析
4.1 实验设置
为了测试所提算法的性能,下面将对算法进行模拟网络和真实社交网络数据的实验测试。将所提算法命名为PSOSB,算法用到的参数设置如下:惯性系数ω设置为经典值0.729,粒子群学习因子c1和c2均设置为1.494,粒子群种群大小pop和算法迭代次数gmax均设置为100。文中采用的对比算法为文献[15]提出的基于买卖提优化结构平衡算法MemeSB,该算法的交叉概率和变异概率分别设置为0.8和0.2,其种群大小和算法迭代次数均设置为100。
实验中用到的模拟网络数据为文献中用到的两个网络AN1 和AN2[16],该网络由28 个节点组成,分成了3 个社区,且该网络是结构平衡的。该实验主要验证AN1网络和AN2网络,4个网络的属性如表1所示。
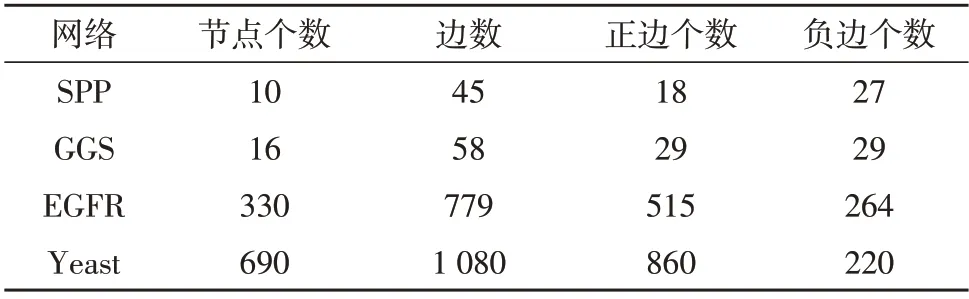
表1 真实网络数据属性统计表
4.2 模拟数据测试
由于文中算法和对比算法都是迭代算法,因此在实验中分别对文中算法和对比算法独立运行30次。
PSOSB 算法和MemeSB 算法30 次独立运行后得到的能量函数H(s)的值均为0,这表明两种算法均找到了网络的平衡结构。图5 和6 分別展示了AN1 网络和AN2网络的网络平衡结构图。从图5和6可以看出,AN1 网络和AN2 网络都被分成了3 个社区,且每个社区内部的节点都是正边连接的,社区之间的节点均为负边连接,这完全符合网络结构平衡的定义。
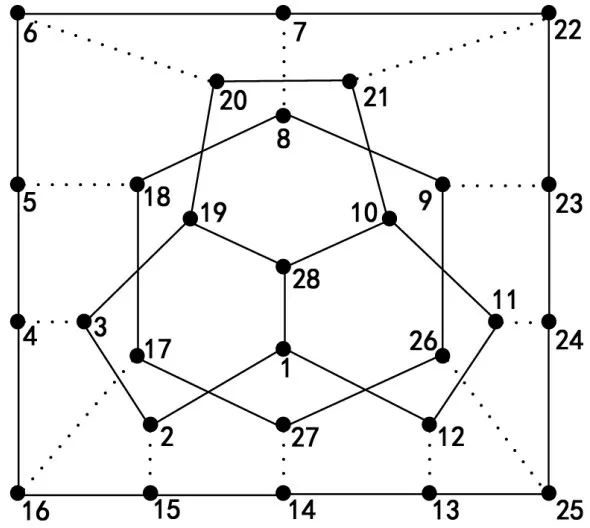
图5 网络AN1的平衡结构图
实验中发现,在对AN1 和AN2 网络进行测试时,文中算法PSOSB 和对比算法MemeSB 均得到相同的结果,且算法稳定。
在AN1 和AN2 网络上,文中算法和对比算法的实验结果一样,这是因为这两个网络的规模太小,两种算法均能很容易找到问题的最优解。虽然在AN1和AN2 网络上两种算法得到了相同的实验结果,但是文中算法比对比算法具有更快的收敛速度,文中算法PSOSB 在AN1 和AN2 网络上的实验性能要明显优于MemeSB 算法。
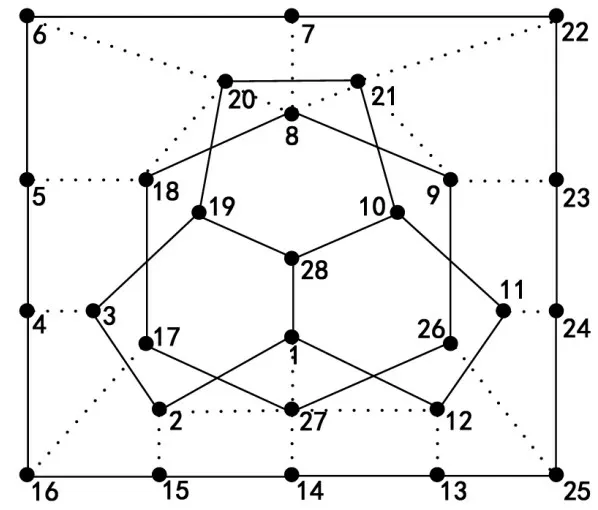
图6 网络AN2的平衡结构图
文中算法是基于粒子群优化的,在粒子群优化算法中,全局最优个体引导整个种群快速向问题的最优解逼近。另外,文中算法在设计上充分利用了网络的结构信息,所设计的粒子状态更新方程能够加速粒子的全局寻优速度。虽然对比算法加入了局部搜索策略,但是该策略是基于贪婪算法的,贪婪算法容易使算法陷入局部最优,而且贪婪算法的计算代价很高。
由于PSOSB 算法和MemeSB 算法都是随机搜索算法,即算法每次独立运行的结果都不相同,因此有必要讨论算法的稳定性。图7 展示了PSOSB 算法和MemeSB 算法在AN1 网络数据和AN2 网络数据上30次独立运行得到的统计结果盒图展示。
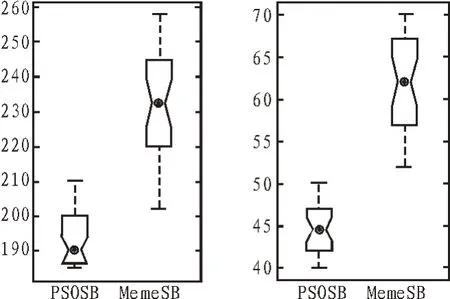
图7 在AN1和AN1网络上的算法稳定性对比实验
盒图反映的是算法多次运行得到结果的统计分布情况,盒图的长短反映了算法的稳定情况。对于一个较为稳定的算法而言,盒图长度相对较短。从图7 可以看出,PSOSB 算法30 运行的盒图长度比MemeSB 短,这说明PSOSB 相对于MemeSB 更稳定;且从盒图的数据分布情况也可以看出,在AN1网络和AN2 网络上,文中算法优化得到的最小能量函数值比对比算法小,实验再次证明了所提算法的有效性。
5 结束语
对社交网络的平衡结构展开研究具有重要的意义。为了实现社交网络的结构平衡,文中从优化的角度出发,首先将网络结构平衡问题转换成优化问题,其次提出了一种基于粒子群优化的求解结构平衡问题的算法。提出的算法不仅可以实现网络的结构平衡,还可以挖掘网络中隐藏的社区结构。算法的有效性在模拟数据和真实网络数据上得到了验证。下一步工作将研究设计高效的局部学习策略,以提高算法的全局搜索能力;另一方面,将研究和实现算法的并行化以实现算法对大数据网络的处理,特别是动态的复杂网络结构平衡是未来值得继续研究的方向。
