载货汽车驱动桥壳的有限元仿真研究

2021-07-30白顺平王振兴陈国磊曹增文

机械工程与自动化 2021年2期

关键词：桥壳半轴套筒

白顺平，王振兴，陈国磊，曹增文

(1.新疆天池能源有限责任公司，新疆昌吉 831100;2.河北建筑工程学院，河北张家口 075000)

0 引言

驱动桥在车辆动力传递过程中，受力条件复杂，传递的载荷较大，在货车行驶过程中，主要实现增大扭矩、降低速度、改变转矩的传递方向等作用[1]。本文针对某轻型货车的钢板焊接式冲压桥壳开展研究，对于驱动桥壳的设计具有一定的指导意义。

1 有限元法原理

有限元法将连续介质材料划分为网格单元节点，通过对不同单元节点的迭代求解，计算材料整体的形变受力等,即先化整为零，再积零为整[2]。有限元法的计算过程是一个较为复杂的数值迭代计算过程，其既需要计算单元内的应变应力，还需要对单元之间的节点应力进行求解。现阶段被广泛采用的有限元计算软件包括ANSYS等大型计算求解软件，该方法目前已经被广泛应用于各个行业分析中，适用范围广，认可程度高[3]。

2 驱动桥壳的建模及有限元分析

2.1 驱动桥壳三维建模

经测量，驱动桥壳的总长度2 116 mm，法兰间距1 205 mm，套管长度293 mm，钢板中心距930 mm，总质量195 kg，材料弹性模量206 GPa，屈服极限620 MPa。

根据测得的参数，在SolidWorks中建立了驱动桥壳的三维实体模型。在建模过程中，主要进行了以下简化：

(1) 去除了圆角和倒角结构。

(2) 去掉了一些附属连接件，只留下驱动桥壳的主体结构，便于开展有限元网格划分等。

建立的驱动桥壳三维模型如图1所示。

图1 驱动桥壳三维模型

2.2 模型网格划分

在Workbench中选择静力学分析模块，导入建立的驱动桥壳的三维模型IGS文件，定义材料属性为Q460低合金高强度钢，弹性模量为206 GPa，泊松比为0.280，材料密度为7 850 kg/m3。之后采用自动划分网格的方式划分网格单元，得到7 768个实体单元和15 200个节点，如图2所示。

图2 驱动桥壳网格单元模型

2.3 四种工况下驱动桥壳的受力校核

对于驱动桥壳的受力分析，一般需要分析满载静止工况、最大驱动力工况、最大制动力工况和最大侧向力工况的受力状况，进而验证驱动桥壳的实际工作状况是否满足使用需求[4]。已知该驱动桥壳承载的货车整车装备质量为7 900 kg，货车总质量为16 000 kg，货车最高车速110 km/h，轴距4.5 m，后轮轮距为1.8 m，钢板中心距为0.93 m，最大扭矩为1 400 N·m。对驱动桥壳进行有限元校核，需要进行一些简单的等效计算，然后开展分析[5-7]。

2.3.1 满载静止工况静强度分析

货车静止于水平路面且处于满载工况时，认为货车受力主要沿着垂直方向，该承载力主要作用于货车后桥上，且水平和侧向方向均认为不受力。采用均分简化的方法，货车后桥总载荷为100 kN，作用于两端弹簧座的均分载荷各为50 kN。

在驱动桥壳上添加约束和载荷，求解得到驱动桥壳的等效应力云图如图3所示。由图3可知，桥壳的最大等效应力处于两端驱动轴轴套与桥壳主体部分的连接位置，因此该位置在静止满载工况处于较为危险的工作状态，经分析，最大应力约107.58 MPa，小于材料的屈服极限620 MPa，满足要求。

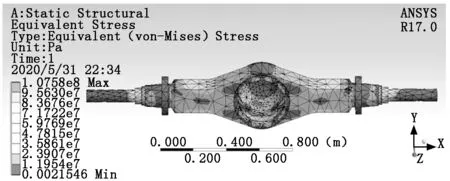
图3 满载静止工况桥壳等效应力云图

驱动桥壳最大等效应变分布状况如图4所示。最大应变位于半轴套筒与桥壳主体的过渡连接处，最大应变为7.97×10-4。在桥壳后盖部位隆起部分和前端面两侧位置，桥壳产生了较大的变形，这两处位置的工况较为恶劣。分析得知，满载静止工况下桥壳产生了最大值为0.10 mm的形变。经相关公式计算得每米变形量为5.6×10-2mm。根据《汽车驱动桥台架试验评价指标/QC/T534—1999》(以下简称《指标》)可知，满载静止工况下后轴轮距最大变形不大于1.5 mm/m，该结果符合国家标准。

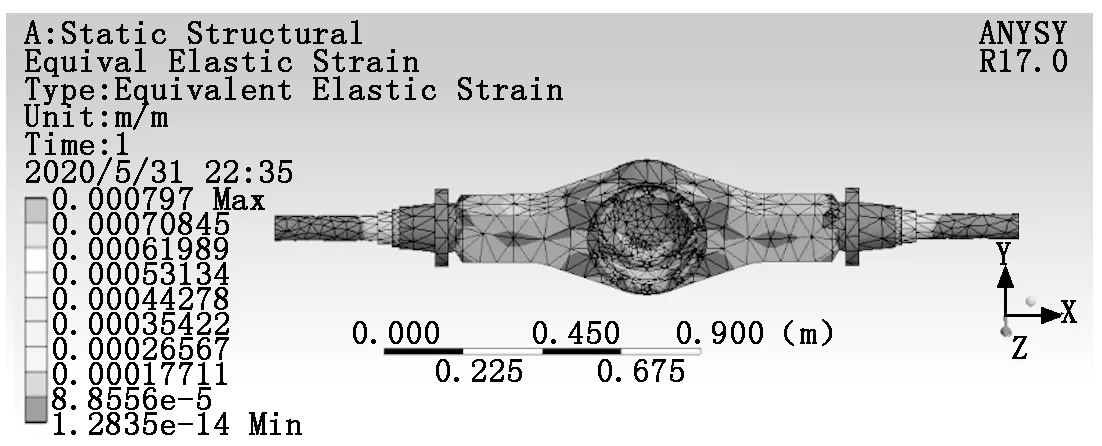
图4 满载静止工况下桥壳等效应变云图

2.3.2 最大驱动力工况强度分析

当货车以最大驱动力前进时，车辆后轴荷具有后移的趋势，桥壳此时受到自身及载重的垂直压力、驱动车轮沿着轮缘的切向牵引力以及后轴传递转矩过程中的反力矩作用桥壳上的力。采用有限元分析方法，需要添加限制桥壳水平方向和沿轴线方向上平动与转动的约束，同时施加在竖直方向限制驱动桥移动的约束。考虑后轴后移趋势产生的影响，驱动桥轴向载荷会增加至垂向载荷120 kN工况，此时两侧弹簧底座分量各为60 kN。

图5为最大驱动力工况下桥壳的等效应力分布云图，此时，桥壳的最大等效应力位置仍然处于半轴套筒与后桥桥壳主体部分连接处，约129 MPa，小于桥壳材料的屈服极限值620 MPa，满足要求。

图5 最大驱动力工况下桥壳等效应力云图

图6为最大驱动力工况下桥壳等效应变云图。由图6可知，桥壳最大等效应变与最大应力处于相同位置，最大应变为9.56×10-4。后桥桥壳的最大变形量位于两弹簧底座之间的前端面的边缘位置，该部位此时的最大形变位移为0.27 mm，经相关公式计算得每米变形为1.5×10-1mm。根据《指标》可知，满足国家标准。

图6 最大驱动力工况下桥壳等效应变云图

2.3.3 最大制动力工况下的强度分析

当货车以最大制动力行驶时，轴荷具有向前移动的趋势，此工况下后轴桥壳的受力有所减小。桥壳此时受到自身及载重的垂直压力、驱动车轮沿着轮缘的切向牵引力以及后轴传递转矩过程中的反力矩作用桥壳上的力。此工况下垂向载荷为90 kN，两端弹簧底座上分布载荷各为45 kN。

图7为最大制动力工况下桥壳应力分布云图，后桥桥壳的最大等效应力位于半轴套筒与后桥桥壳主体部分连接处，最大应力值为96 MPa，远小于桥壳材料的屈服极限值620 MPa，满足设计要求。

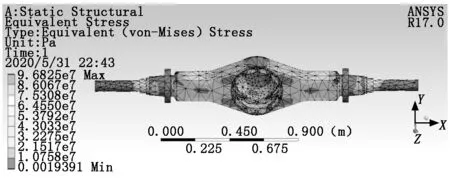
图7 最大制动力工况下桥壳等效应力云图

图8为最大制动力工况下桥壳等效应变云图。由图8可得桥壳最大等效应变位于半轴套筒与桥壳主体的过渡连接处，最大应变为7.17×10-4。后桥桥壳的最大变形位于两弹簧底座之间的前端面边缘位置，最大形变位移0.32 mm，经相关公式计算得每米变形为1.78×10-1mm。由《指标》可知，满足国家标准。

图8 最大制动力工况下桥壳等效应变云图

2.3.4 最大侧向力工况下的强度分析

当货车处于最大侧向力行驶工况下，桥壳受到载货重量的垂向作用力、自重和驱动轮的切向牵引力。此工况下垂向载荷为100 kN，作用于单侧弹簧底座上。

图9为最大侧向力工况下桥壳等效应力云图，由图9可知，桥壳的等效应力最大值出现在半轴套筒与后桥桥壳主体部分连接处和单侧的钢板弹簧座附近，此时最大应力值为135 MPa，小于桥壳材料的屈服极限值620 MPa，满足要求。

图9 最大侧向力工况下桥壳等效应力云图

图10为最大侧向力工况下桥壳等效应变云图。由图10可知，最大驱动力工况下桥壳等效应变最大值位于半轴套筒与桥壳主体的过渡连接处，最大应变值为1.17×10-3。后桥桥壳的最大变形位置处于单侧钢板弹簧座处，最大位移为0.9 mm，经相关公式计算得每米变形为5.1×10-1mm。由《指标》可知，满足国家标准。