匀转速下等质量非球形颗粒运动特性研究*

张浩强，蔡 柳，卢森幸，林彦伯

(河池学院，广西 宜州 546300)

0 引言

研究颗粒物料的流动规律对于矿石筛选、粮食筛分、物料转运以及卸料等作业过程具有重要意义。由于不同种类物料具有不同的性质、颗粒形状、流动特性等，因此，对颗粒物料流动特性的实验研究工作量大、过程繁琐。DEM(Discrete Element Method)是近年来一种被广泛应用于颗粒物料运动特性研究的方法[1,2]。利用其研究颗粒的运动过程，能够从宏观角度观察颗粒的运动状态，并从颗粒速度、能量分布等角度分析引起物料流动状态变化的原因[3]。大量研究表明，利用DEM研究颗粒物料的流动过程具有一定的参考价值。本文基于DEM方法，研究了四种形状颗粒在匀速转动圆筒中的运动特性。

1 DEM方法简介

应用DEM方法进行研究，需要根据所研究的颗粒特性选择不同的计算模型。例如，低粘结度颗粒(沙土、煤块等)适用于Hertze-Mindlin(no-slip)计算模型，含湿物料(黏土)可以考虑采用JKR模型等[4]。为了研究非球形颗粒的运动特点，本文采用Hertze-Mindlin(no-slip)模型，计算非球形颗粒(塑料球)在匀速转动圆筒容器下的流动特性。该计算模型中，颗粒间的法向力为：

(1)

其中：E*为颗粒等效弹性模量；R*为颗粒等效接触半径；α为颗粒间法向重叠量。

法向阻尼力为：

(2)

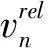
颗粒间切向力为：

Ft=-Stδ.

(3)

其中：St为颗粒的切向刚度；δ为颗粒间切向位移。

颗粒间切向阻尼力为：

(4)

2 模型建立及仿真分析

2.1 颗粒模型的建立

为了研究不同形状的颗粒在匀转速过程中的运动特性，分别设置了四种形状的塑料颗粒，即球形、直线形、三角形和正方形四种颗粒模样，如图1所示。它们是自然界中普遍存在的形状，许多物料均可以被简化为这几种颗粒形状或它们的相互组合。

图1 不同形状的颗粒模型

根据文献[5]中的试验和仿真结果，选取塑料小球作为研究非球形颗粒流动特性的对象，塑料小球与钢的物料属性如表1所示。材料间的接触参数如表2所示。

表1 塑料小球与钢的物料属性参数

表2 材料间的接触参数

2.2 仿真数值模型的建立

在仿真过程中，生成了存放颗粒物料的圆筒，圆筒高60 mm、半径140 mm，用以存放不同形状的塑料小球。在仿真过程初始阶段，分别在圆筒中生成了球形、直线形、三角形和正方形的塑料小球，保证圆筒内存放的小球质量和体积相近，用以对比分析形状变化造成的流动变化规律，如图2所示。设置圆筒绕轴线的旋转速度为720 °/s，仿真过程中采用20%的瑞丽时间步长，步长迭代时间约为1.94×10-6s[6]，仿真时长0.5 s，对比观察颗粒的流动特征。

图2 仿真的圆筒与颗粒模型

仿真过程中，为了充分考虑形状等参数对颗粒运动特性的影响，设置颗粒的质量、体积保持一致，但是颗粒的数量有一定的差别，仿真生成颗粒的特征参数,如表3所示。

表3 生成颗粒的特征

3 仿真结果分析

仿真结束后，分别对四种形状塑料小球的运动特点进行分析。

3.1 颗粒运动速度特性

分别观察四种形状的塑料球在圆筒匀速转动下形成的颗粒运动状态，如图3所示。随着圆筒的转动，与筒壁接触的颗粒由于摩擦作用，加速旋转，并且将外部的动能向内传递。

由图3可知，颗粒转动加速后分别呈现出外圈高速、中圈中速和内圈低速的转动状态，这与实际运动认知常识是相符合的。

图3 四种形状颗粒加速后的稳定状态

3.2 颗粒运动过程受力特性

导出颗粒运动过程中的受力数据，不同形状颗粒在圆筒以720 °/s的转速旋转情况下，颗粒的总受力状态如图4所示。

图4 四种形状颗粒加速过程中的总受力变化情况

由图4分析可知：颗粒由静止到运动的过程中，其受力大小随着时间呈现出不同的波动规律；在0.25 s之前，颗粒整体受力波动较大，0.25 s之后，塑料颗粒受力的波动幅度趋于稳定状态，受力较小但不为0。

从形状与受力角度分析，球形塑料小球的总受力初始值最大，但是在后期波动中总是小于其他三种形状的颗粒；三角形塑料小球的颗粒受力最大，其他两种形状小球的总受力介于球形与三角形小球之间。分析认为，这可能是由于三角形塑料小球与其周边小球接触点位较多、配位数较大，因此在加速过程中相互之间受到的阻力较大，因此，其加速过程受力较大，同时加速时间较长。

由于在仿真过程中，颗粒的质量、体积相同，但是颗粒数量不同，因此分析塑料小球的平均受力状态对于分析形状造成的受力变化具有一定价值的参考意义。颗粒在加速过程中，受力均值的变化如图5所示。

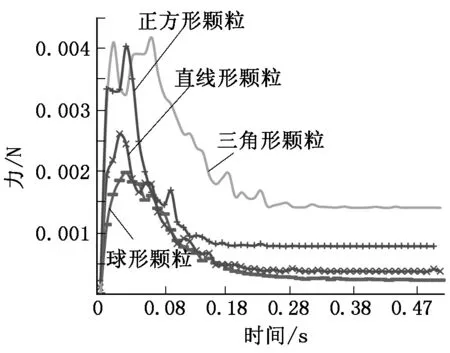
图5 不同形状小球运动过程中平均受力的变化

从不同形状塑料小球的加速运动过程中的平均受力大小可以看出：三角形颗粒与正方形颗粒初始阶段的受力均大于球形颗粒与直线形颗粒；在后续过程中，三角形颗粒的受力均值大于其他三种形状颗粒的受力值，说明三角形颗粒稳定转动状态下其内部存在较大的分布力；在颗粒随着筒壁稳定运转阶段，三角形颗粒的稳定旋转受力均值约为球形颗粒和直线形颗粒的3.75倍和3倍，三角形颗粒在这四种颗粒中的受力特点最为特殊。

研究颗粒的受力状态对于分析不同形状颗粒的受力特点具有一定的指导意义，同时，研究颗粒的受力大小与预处理颗粒的形状对于颗粒破碎过程中减小机械装置的摩擦磨损具有一定的指导意义。

3.3 颗粒运动流动特性

通过设置颗粒显示状态为速度矢量方式，可得到塑料颗粒由初始时刻至加速稳定阶段其速度矢量的变化情况。由于不同形状呈现的速度矢量变化规律基本相同，因此本文只给出了球形颗粒在加速过程中的运动规律，如图6所示。

图6 球形颗粒在加速过程中的速度矢量

由图6可知：颗粒由静止加速至稳定旋转过程中，外圈颗粒的速度逐渐增加，可知颗粒的动能来自于与圆筒外壁的摩擦；随着时间推移，外圈高速运动颗粒半径逐渐减小，最终至t=0.5 s后，颗粒呈现出外、中和内圈三个不同速度层次的速度状态。该过程对于研究颗粒的加速运动规律具有一定的指导意义。

4 结论

本文基于DEM方法，分析了四种形状颗粒在匀转速圆筒中的流动特性，主要得到了以下结论：

(1) 基于DEM对小规模颗粒的加速运动特性进行分析是可行的。

(2) 不同形状塑料颗粒在加速运动过程中的受力大小有一定的差异。三角形颗粒，即棱角较为突出的颗粒在不稳定运动阶段的受力明显大于其他形状颗粒，颗粒的平均受力大小也呈现出了类似的关系。

(3) 根据颗粒形状特点，可以在处理不同形状颗粒过程中进行预处理以减轻颗粒的受力或者相关机械的磨损等。例如，球形或者正方形颗粒对于破碎机械的磨损会小于三角形颗粒引起的磨损。