基于风致振动的剪切模式压电能量收集结构的数值模拟
2021-07-30于慧慧王永耀林杉杉
于慧慧,李 莉,王永耀,林杉杉
(沈阳化工大学 计算机科学与技术学院,辽宁 沈阳 110142)
0 引 言
电子设备通常都依赖于传统的化学电池获取能量,但是传统的化学电池体积较大,对环境有一定的污染,而且对许多领域来说频繁更换化学电池十分烦琐。风致振动效应是将环境中的风能通过某种方式转化为振动能量,进而通过压电效应、磁电效应以及磁致伸缩效应等转化为电能。由于压电效应具有结构简单、输出电压和功率密度高的优点,因此以压电效应的方式转化电能成为振动能量采集的主要研究方向之一[1,2]。
近年来,一些学者开始利用风致振动现象进行压电能量收集,其中利用涡致振动产生的漩涡作用在压电材料上,使压电材料产生机械振动后将机械能转化为电能是比较常用的方式[3]。目前国内外关于风致振动压电能量收集技术的研究已经取得了大量成果,其中Vatansever D等利用压电陶瓷材料进行压电能量收集实验的研究,研究结果表明在风速为10 m/s,压电陶瓷长度为14 cm的情况下,压电陶瓷单层复合样品产生的电压为45 V[4]。丁林等提出了一种下端为自由端,上端中心与压电片连接,压电片上部固定于风洞顶面的压电能量收集装置,研究结果表明钝体为方柱,压电片长度为10.5 cm时,其振幅、输出电压以及功率最大分别为0.15 m、0.55 V、0.378 μW[5]。郭修宇对圆柱或方柱后接柔性挡板进行了仿真与风力场实验研究,研究结果表明流速为10 m/s、圆柱体直径为60 mm、压电悬臂梁长度为75 mm时,产生的电压最大为7.2 V[6]。张敏等提出了一种双晶压电悬臂梁下端连接小质量块,上端固定于圆柱顶部,两根弹簧平行连接在垂直于压电臂面的平面,另一端固定在风洞内壁上的压电能量收集装置,研究结果表明随着风速的增加,圆筒和压电悬臂梁的振幅逐渐增大,输出电压也逐渐增大,风速为11.8 m/s时,电压和振幅达到最大值,分别为3.391 V和7.66 mm[7]。Akaydin H D等对一个直径为19.8 mm的空心圆柱加单悬臂梁压电装置进行了风洞实验研究,研究结果获得的最大功率为0.1 mW。以上研究充分证明了风中涡致振动压电能量收集的可行性[8]。
在压电振动俘能结构中,压电材料主要有d33纵向模式、d31横向模式以及d15剪切模式3种工作模式。目前关于压电振动俘能技术的研究多采用d33和d31工作模式,对剪切模式压电振动能量收集技术的研究较少,而压电材料的压电常数均具有d15>d33>d31的关系,d15模式与d33和d31模式相比可以有效提高输出功率,并且由于悬臂梁在共振情况下的梁体变形剧烈,压电陶瓷材料的制造工艺虽然成熟,但材料本身仍然非常脆,因此在周期负载作用下易发生疲劳断裂[9,10]。工作在d15剪切模式的压电材料可以在形变较小的情况下获得较大的输出功率,不仅可以提高发电效率,而且还能减少压电陶瓷的疲劳损伤,增长器件的使用寿命。
本文对课题组提出的一种并联双晶片剪切式压电悬臂梁结构进行了数值模拟,通过调节风速、阻流体与压电能量收集结构之间间距等参数进行分组仿真,得到最优参数,为风致振动压电能量收集技术的实验研究提供参考。
1 压电能量收集结构及数值分析方法
1.1 压电能量收集结构
并联双晶片剪切式压电能量收集结构如图1所示。结构由压电悬臂梁上端连接轻质圆筒直立于空气流中构成,悬臂梁中间铜片作为基板,压电陶瓷附着在铜基板的两侧,上接阻流圆管,风沿x方向流动,经阻流圆管后产生交替脱落的旋涡,驱动阻流圆管在y方向发生摆动,从而带动下方支撑结构的自由端发生位移,进而驱动压电片产生切变,将机械能转化为电能。这种结构通过悬臂梁放大了振动位移,增加了梁固定端压电片的切向应变,且充分发挥了压电材料剪切机电耦合系数高的优势,结构简单,易于制作,材料使用寿命长,能量转换效率高。

图1 并联双晶片剪切式压电能量收集结构图
1.2 数值分析方法
建立风致振动剪切模式压电俘能结构的流-固-电耦合数学模型,对该结构在风中的涡致振动和压电效应进行数值计算。采用范德波尔方程来描述流体的动力学特性,流体与圆管之间的耦合作用采用Facchinetti & de Langre提出的尾流振子数学经验模型计算,圆管驱动支撑梁的单自由度运动方程通过简化Euler-Bernoulli梁方程来计算,压电材料的剪切压电效应利用压电本构方程来计算。
1.2.1 涡致振动理论分析
根据剪切式压电能量收集结构的设计,单自由度俘能结构力电原理简化如图2所示。

图2 单自由度俘能结构风致振动力电原理图
由图2可知来流方向为x方向,圆管在y方向自由振动,Ux为流速,D为圆管直径,ms为圆管质量,ky为支撑结构的弹性刚度,Ry为压电梁的等效电阻,cy为支撑结构等效阻尼。弹性支承的单自由度圆管的y方向振动可以用线性振子方程表示为:

式中,my=ms+mf,mf=CMρD2π/4,μ=(ms+mf)/ρD2,mf为流体附加质量,ρ为流体密度,μ为无量纲质量比,CM为附加质量系数。线性阻尼cy包括支撑结构的粘滞耗散cs和流体附加阻尼cf,分别表示为:

式中,γ是振幅函数,与结构的平均截面阻力系数有关;涡致振动角频率ω=ωf=2πStU/D;St为斯特劳哈尔数。
涡致振动圆柱尾流的波动特性则可以用满足范德波尔方程的非线性振子来模拟,即:

式中,ωf为涡流的脱涡频率,q为尾流变量,ε为尾流振荡器模型的参数。
结构与尾流振子耦合的振动方程可表示为:

这里空间坐标Y=uy/D,δ=ωs/ωf为约化角频率,有,无量纲耦合项。
将圆柱单自由度涡致振动方程作用于支撑梁,由图2坐标系可知横向载荷对称与x-z平面,则通过Euler-Bernoulli梁模型描述支撑梁的运动情况为:

式中,Fs和M分别是梁横截面的剪力和弯矩,EI是横截面的弯曲刚度,p(z)为沿梁长方向分布的横向载荷的强度。
1.2.2 剪切式压电悬臂梁结构理论分析
剪切模式压电本构方程为:

式中,T5和S5分别代表剪应力和剪应变,T3和T3代表轴向应力和应变,E1和D1分别为沿厚度方向的电场和电位移,e15为压电系数。这里的数字代表图1和图2中压电梁的方向,“1”代表y方向,“3”代表z方向,“5”代表“13”面(y-z面)。
电功率计算公式为:

圆柱阻流体上的压电耦合使用无量纲电功率进行计算,压电能量收集效率为:

2 流固耦合数值模拟及结果分析
利用ANSYS软件对剪切式压电能量收集结构在流体域进行流固耦合有限元仿真。将剪切式压电能量收集结构直接立于流体域中,其底端固定,上端自由,当流体流经阻流体时会在阻流体后方产生交替脱落的漩涡,漩涡作用是在压电结构上使压电结构产生规律性的振动。利用ICEM进行网格划分,其流固耦合的具体参数如表1所示,流体域和结构模型分别如图3(a)和图3(b)所示。

表1 轻质材料与流体域参数表

图3 剪切式压电能量收集结构流固耦合模型
阻流体与阻流圆管均为直径D=0.01m的圆柱,两者中心距L分别取3D、4D、5D以及6D进行流固耦合求解,经后处理得到流场随间距的变化规律如图4所示。

图4 不同中心距下的流线图
由图4可知,L=3D和L=4D时,流体流经阻流体后出现两个明显的漩涡,流体被分为两部分,在形成完整脱落的漩涡之前交替覆盖下游的压电结构,阻流体与压电结构之间出现横向流动,并随着间距的增大,横向流动变得越发强烈。L=5D时,流体流经阻流体后,产生完整的周期脱落的漩涡,阻流体对压电结构的来流有一定影响。L=6D时,阻流体与压电结构之间距离较大,阻流体产生漩涡脱落,其流动状态近似于单个圆柱体,对下游的压电结构影响较小。
为了使数值模拟更加接近真实,更具现实意义,参考自然界风力等级对照表,结合流场随阻流体与压电结构间距的变化规律,本文选取中心距为L=3D、L=4D、L=5D、L=6D,流速为7~14 m/s进行分组的流固耦合模拟,分析压电结构的振幅响应结果。中心距为L=5D,流速为14 m/s时,压电结构产生的形变最大,形变情况图如图5所示,压电结构的位移峰值随中心距和风速的变化情况如图6所示。
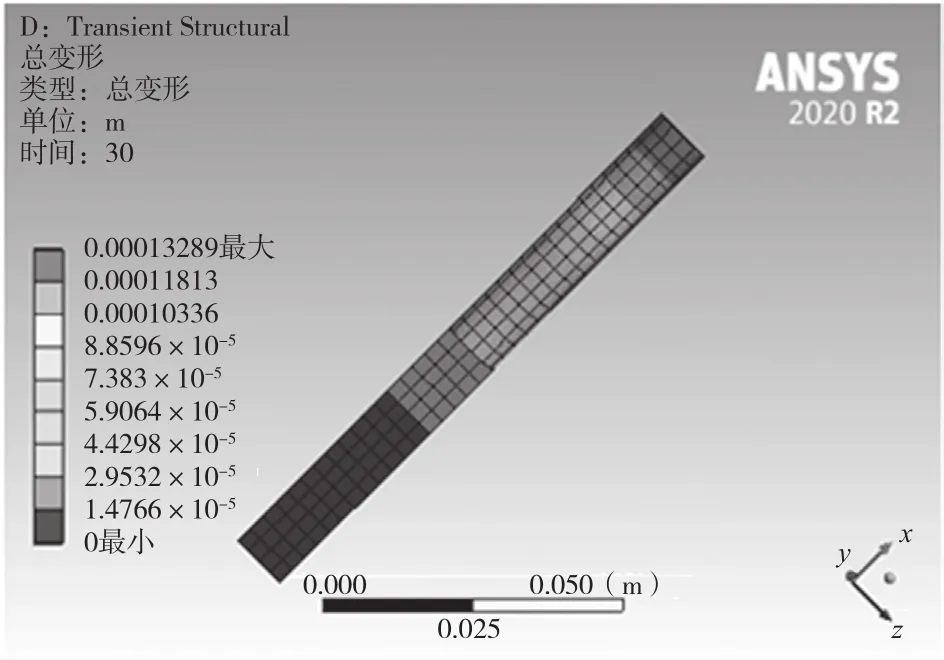
图5 压电结构形变情况图
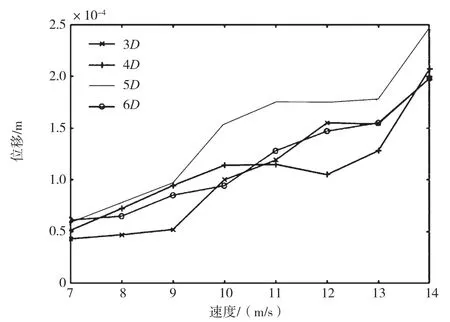
图6 不同中心距的振幅响应-风速图
由图6可知,压电结构的振幅响应均随着风速的增加而增加。流速在7~10 m/s之间变化时,压电结构在不同间距下的位移峰值相差不大,流速在11~14 m/s之间变化时,不同中心距下的位移峰值差距逐渐增大,中心距为5D时产生的位移最大。当中心距为3D和4D时,由于阻流体与压电结构之间的距离较近,流体流经阻流体后,在产生周期脱落的漩涡之前便开始绕过压电结构,因此对压电结构的振幅影响较小。当中心距为5D时,流体流经阻流体后产生周期脱落的漩涡,由于间距适中,脱落的漩涡正好作用在下游的压电结构上,使压电结构产生往复变形,其振幅响应最为明显,为2.47×10-4m。当中心距为6D时,由于阻流体与压电结构距离较远,脱落的漩涡对压电结构作用较小,其压电结构的振幅响应也明显减小。压电结构不同间距下的振幅响应与流场随间距的变化规律相一致。
3 压电耦合数值模拟及结果分析
本文采用剪切模式压电能量收集结构,阻流圆管在流体作用下产生了规律性的振动,带动下端的压电悬臂梁以相同的振幅振动,从而产生电压,实现压电耦合。将剪切模式压电能量收集结构形变产生的幅值作为压电耦合的机械载荷输入,其压电耦合数值模拟的具体参数如表2所示,压电耦合模拟后产生的电压分布云图和电压时程曲线分别如图7和图8所示。

表2 压电悬臂梁具体参数表

图8 电压时程曲线图
从图7中可以看出,将流体域中流固耦合模拟所得到的振幅响应作为载荷施加在剪切式压电能量收集结构上,压电耦合求解后得到的悬臂梁压电层上产生的电压呈阶梯状的分布,与阻流圆管连接的位置即压电层上端产生的位移形变量最大,产生的电压也最大,中间部分及下端产生的位移形变量逐渐减小,产生的电压也越来越小。由图8中可以看出,当压电结构受阻流体产生的漩涡的影响而规律性的摆动时,压电悬臂梁产生了规律的正弦电压曲线。这证明利用风致振动作用,可以使剪切式压电能量收集结构产生周期变化的电压,从而可以进行能量的收集。
当阻流体与压电结构中心距为5D时,压电结构的振幅最大,振幅越大,产生的电压也越大,因此选取L=5D,风速为7~14 m/s对剪切式压电能量收集结构进行压电耦合数值模拟,得到的电压随风速的峰值变化曲线如图9所示。

图9 风速-电压折线图
由图9可以看出,压电结构产生的电压随风速的变化趋势与振幅随风速的变化趋势相同,均随风速的增大而增大。风速在7~10 m/s时,电压上升的较快,10~13 m/s时,电压的上升趋势比较缓慢,14 m/s时达到峰值4.69 V。证明了利用剪切式压电能量收集结构进行能量收集的可能性,对压电结构产生的电压经能量收集电路整流滤波操作后,便可用于对微电子设备的供电。
4 结 论
本文利用ANSYS仿真软件对课题组提出的基于风致振动的剪切模式压电能量收集结构进行了流固耦合和压电耦合数值模拟,对不同风速和中心距下剪切模式压电能量收集结构的振幅响应和产生的电压情况进行了分组分析对比。首先推导剪切式的压电能量收集结构的风致振动数值计算公式,为风致振动能量的收集提供了理论支撑。然后对能量收集结构进行了流固耦合数值模拟,分析不同间距下流场的变化规律,为研究风速中心距对压电结构的影响进行了分组仿真,并与流场随间距的变化规律进行对比。最后对剪切式压电结构进行了压电耦合数值模拟,分析了不同风速下电压的变化情况,得出以下结论。
一是分析不同中心距下的流线图,随着中心距的增大,上游阻流体的漩涡逐渐脱落,逐渐趋于单个圆柱绕流,当中心距为5D时,脱落的漩涡刚好作用在阻流圆管上。二是选取风速为7~14 m/s,中心距为3D~6D,压电结构的振幅响应随风速的增大而增大,振幅响应变化规律与流场随中心距的变化规律相一致。当中心距为5D时,压电结构产生规律性的振动,振幅响应最大为2.47×10-4m。三是将中心距为5D时流固耦合得到的振幅响应作为压电结构的载荷输入进行压电耦合数值模拟,得到电压随风速的变化曲线。结果表明,压电结构产生了规律的正弦电压曲线,得到的电压幅值变化规律与振幅响应变化规律相一致,风速为14 m/s时,电压最大值可达4.69 V。本文的研究结果证明了剪切式压电能量收集的可行性,为后续的实验研究提供了理论参考。
