一种高效的权值约束可达性查询处理算法
2021-07-30成梦佳周军锋
成梦佳,杜 明,周军锋
(东华大学,上海 松江 200000)
0 引言
互联网技术的发展与应用,催生出了海量的数据[1-2]。图作为一种常见的数据结构,能够较好地抽象描述数据之间的关联性。因此,图被广泛应用在各个领域中,如通信网络、生物信息网络、道路网络等[3-5]。
传统的可达性查询[6-11]用来回答给定的源点和终点之间是否存在可达的路径。但是实际网络中,顶点和边往往都会包含权值,例如通信网络中站点间的通讯交流就是通过带宽约束,保证多媒体流端到端的服务质量。因此,在回答可达性查询时考虑权值约束更贴合实际,有较高的研究价值。
现有的基于权值约束的可达性查询相关是Edge_Index[12],它的主要思想是通过边上的权值构建索引树,预先存储先序遍历索引树得到的序列,尽管该算法的查询效率很高,但是构建的索引占用的空间内存过大,无法在内存有限的环境下处理顶点规模大的数据图。
针对以上问题,本文提出一种基于权值约束的 2-hop索引算法。该算法基于顶点的度来确定顶点的处理顺序,然后基于该顺序来构建加权图的 2-hop索引。其基本思想是将加权图上的权值约束可达查询转换为基于顶点标签的集合交集操作,从而减小构建索引的时间和空间代价。实验结果表明,本文提出的方法能有效地降低索引规模,提高回答查询的响应速度。
1 问题定义和相关工作
1.1 相关概念和问题定义
本文基于无向加权图处理权值约束可达性查询的问题。给定无向加权图G=(V,E,∑,w),其中,V表示图G中的顶点集合,E表示G中无向边的集合,∑表示G中权值的集合,w表示每条边上的权值。下文中,用e=(u,v)∈E表示从顶点u到顶点 v的一条边;P(u,v)表示 u到 v的路径;Label(v)={(v1,w1),…,(vi,wi)}表示顶点v的标签集,其中 wi表示 v到 vi的路径上的权值;规定查询q=(u,v,C),其中u、v∈V表示两个查询的顶点,C是随机值表示边上权值约束,可以为≤y、≥x或者[x,y]三种形式。
问题定义 给定一个无向带权图G和一个权值约束查询q,如果从顶点u到顶点v存在一条路径,路径上每条边的权值都满足约束 C,则说明u可达v,否则不可达。
1.2 相关工作
1.2.1 传统可达性查询
可达性查询的相关算法研究可以根据顶点的覆盖情况分为两类:全覆盖索引(Label-only)和部分索引覆盖(Label-G)[13]。
Label-only的主要思想是给图上的每个顶点都构建索引,索引中包含相关的可达信息。处理查询时,通过判断索引中是否存在交集,存在即可达,否则不可达。Label-only类的经典算法主要有PLL[14]算法、TF[15]算法、Path Hop[10]算法。以PLL[14]算法为例,它的主要思路是利用BFS预先为图上每个顶点分别构建 Lin(v)和 Lout(v)标签,Lin(v)表示顶点 v可以到达的其他顶点,Lout(v)表示可以到达v的所有顶点。通过判断两个顶点的出度标签和入度标签是否有交集,来查询可达。PLL方法的索引大小为 O(L×|V|),索引时间为 O(L×|V|×(|V|+|E|)),查询时间为 O(L),其中L表示标签元素个数。
Label-G方法则通过在部分顶点上构建索引,以减少遍历全图的时间。查询时,如果该索引可以回答查询就直接返回结果,否则需要在图上进行BFS或DFS遍历来得到结果。Label-G类的经典算法主要有 GRAIL[16]算法、FELINE[17]算法和IP+[18]算法。以FELINE[17]为例,它的核心思想是利用两个拓扑排序(x,y)去给图上的每个顶点赋予标签,第一个拓扑排序是考虑顶点的入度得到 x的拓扑顺序,第二个拓扑顺序则是基于x的结果得到y的拓扑标签。只有当满足顶点u的x和y拓扑标签都分别小于顶点v的两个相对应的拓扑标签,才能说明顶点 u可达顶点 v,否则说明顶点u和顶点v之间不可达。FELINE方法的索引空间复杂度为 O(|V|),索引构造时间复杂度为O(|E|+|V|×log|V|),查询时间复杂度为 O(|V|+|E|)。
1.2.2 权值约束可达性查询
权值约束可达性查询用于回答在顶点 u和 v之间是否存在一条路径,它每条实值边上的权值均满足给定的权值约束。Miao提出了一种新的构建索引的方法 Edge_Index[12],其主要思想是基于生成树构建一个索引树,通过LCA[19]和RMQ方法求解两个顶点u、v构成区间的最值,即两个顶点的最近公共祖先,得到该祖先结点的 Label值与给定的权值约束进行比较。若 Label满足约束,则证明u可达v,反之不可达。
Edge_Index算法构建索引的时间复杂度为O(|∑||E|),索引的空间复杂度为O(|∑||V|2),查询时间为O(1)。尽管该方法的查询响应时间较快,但是它构建索引时需要预先存储索引树上结点的序号和标签,当图的顶点规模足够大时,仍然会超出内存。换言之,该方法无法在有限的内存环境下处理大规模的数据图。
2 基于权值约束的算法
2.1 权值约束的索引策略
需要注意的是,实际应用中的权值约束有多种形式,如半有界区域≤y、≥x或有界区间[x,y]。在处理上,由于≤y和≥x是对称的,因此本文预先假设查询 q=(u,v,C)中的约束 C的形式为≤y,后文中将会证明本文提出的方法可以很容易地扩展到有界区间[x,y]的处理上。
对于权值约束的可达性查询q=(u,v,C),需要找到顶点u和顶点v之间某一条路径,该路径上所有边的权值都满足约束 C。不难想到,一种直接的方法就是枚举出顶点u到顶点v的路径。考虑到每条路径上的权值与约束之间的关系是不确定的,所以在列举 P(u,v)时需要枚举出所有存在的路径,然后判断每一条路径是否满足约束,当某条路径满足条件时,就给出回答;当遍历完所有的路径仍不满足约束,则给出不可达的结论。
如图1所示,当回答查询 q=(a,g,≤4)时,可得出 P1(a,g)=(a,f,b,g)、P2(a,g)=(a,f,g)、P3(a,g)=(a,f,d,b,c,g)。然后从多条不同的路径中,判断是否存在一条路径,其每条边上的权值都≤4,可知P3满足,即顶点a、g存在满足约束条件的路径,说明在权值约束下点 a可以到达点 g;若每一条路径都不满足条件,则说明a不可达g。

图1 无向加权图GFig.1 Undirected weight graph G
从图 1中可以发现,任意给出两个顶点时,可以在给定的无向图中找到若干条可能的路径。然而当图的规模很大时,枚举出所有 P(a,g),并将所有路径上每条边的权值与给定的权值约束进行判断则会花费大量的时间和空间代价。
当约束为≤y,直接取出路径上边的最大值与约束条件进行比较,若最大值满足约束,则该路径其余边上的权值必然也满足。如图 1,给出查询 q=(a,g,≤4),对于 P(a,g),取 P1(a,g)=(a,f,b,g),w(e)max=w(b,g)=7,7≤4不成立,故 P1(a,g)不可达;P2(a,g)=(a,f,g),w(e)max=w(f,g)=6,6≤4不成立,故 P2(a,g)不可达;P3(a,g)=(a,f,d,b,c,g),w(e)max=w(c,g)=4,4≤4成立,故P3(a,g)上每条边的权值均满足约束。此外,上述例子中,枚举出的P(a,g)有3条路径,分别将7、6、4依次与约束条件判断,如果存储的路径越多,比较次数也会同步增多。但是,如果优先处理 Min{7,6,4}=4,4≤4,即P3就可以直接结束判断。因此在构建2-hop标签时,只需要存储一条权值较小路径上的最大值,当该权值满足约束时,其他边上的权值必然也都满足。构建标签的具体过程如下。
在图1的无向加权图G上,按照每个顶点的度从大到小确定遍历顺序,即 f→g→b→d→c→h→a→e。首先处理顶点 f:Label(f)初始值为(f,0),从 f出发依次访问其余顶点,将顶点 f与其他每个顶点之间较小路径上权值的最大值存入相应顶点的标签中,如P(f,g),则取路径f→d→b→c→g上最大的权值为4,存储标签为(f,4)。在处理顶点g时,当访问到顶点a时,发现顶点g无论经过哪条路径到a都必须经过f,而f已经被处理过,因此无需存入P(a,g),顶点e同理。当处理顶点c时,c有两个相邻顶点b和g,并且点b和g的访问顺序优先于 c,即 c无论访问哪个顶点都可以通过 b或者 g得到相应的标签,所以 Label(c)也无需存入新的标签。根据以上思路处理完所有顶点得到2-hop索引,见表1。

表1 基于所有顶点的2-hop索引Tab.1 2-hop index based on all vertices
2.2 索引的构建
本文提出一种基于权值约束的 2-hop索引方法(Degree Index)。该方法的基本思想为:首先在原图上基于顶点的度得到顶点处理的顺序;然后按照顺序依次进行遍历,结合剪枝策略,构建2-hop标签索引。具体的代码设计如算法1所示。

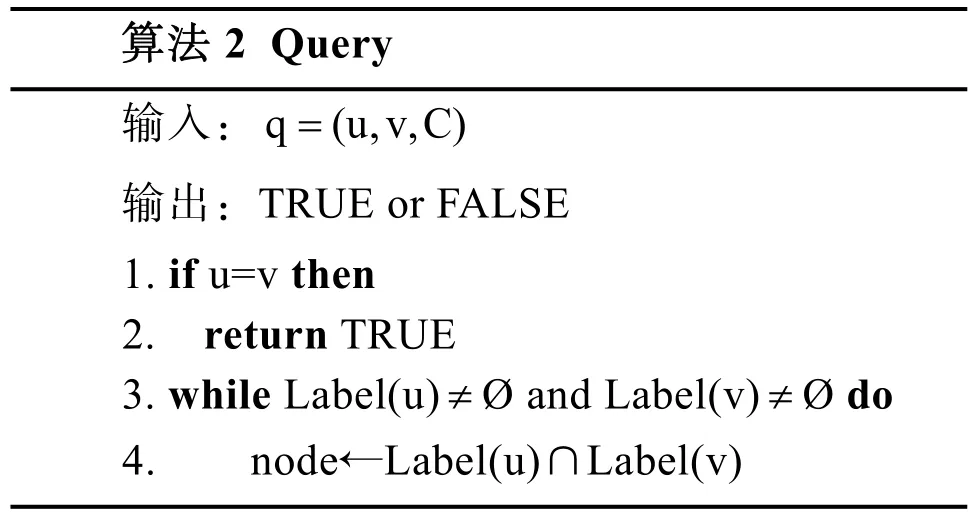
算法1 D e g r e e_I n d e x=输出:所有顶点的L a b e l索引1. N o d e o r d e r←S o r t(d e g r e e, D e s c e n d i n g_o r d e r)2. f o r e a c h v∈N o d e o r d e r d o 3. p u s h v i n t o Q 4. p u s h (v,0) i n t o L a b e l(v)5. w h i l e Q i s n o t e m p t y d o 6. p o p u f r o m Q 7. f o r e a c h u∈E d o 8. Q←(u, m a x(w,w’))9. L a b e l(v)←Q输入: G (V,E,Σ,w)

10. if P(v,w)≤P(u,w) do 11. continue 12. update Label(v)
算法1用来构建所有顶点的2-hop索引。首先按照图上顶点的度降序排列得到处理顺序(第1行);将顶点依次执行入队顺序(第2-3行);标签的初始值为(v,0)(第4行);当队列不为空时,执行出队操作(第5-6行);将路径上边的最大权值存入顶点的标签中(第7-9行);若已有的标签权值大于路径上权值,则不作更新,否则将新的权值存入对应的标签中(第10-12行)。
算法1的时间复杂度为O(|V|2),空间复杂度为 O(|V|×L)(L表示所有顶点的 2-hop标签中的最多个数)。看起来虽然空间复杂度较大,但是该算法结合剪枝优化后的hop点个数远小于图的顶点个数,因此会减少一定程度的2-hop标签索引。
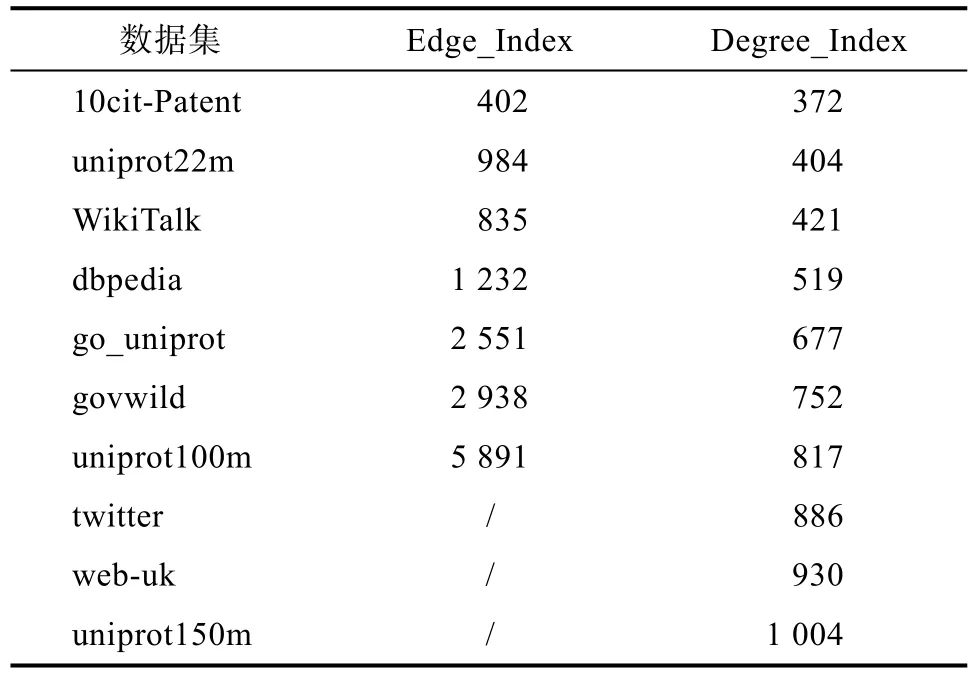
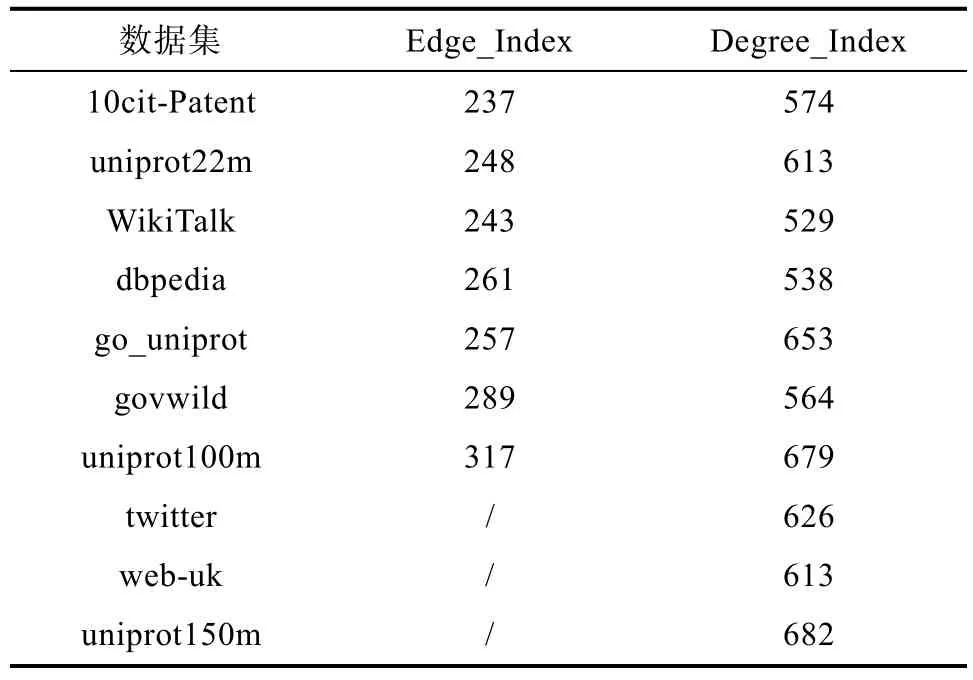
当约束形式为≥x时,即每条边的权值都≥x,故找出权值的最小值与约束条件进行比较判断即可;当约束形式为[x,y]时,可以将其看做是两个约束条件,即同时满足≥x和≤y。而对于≥x情况可以先反向排除所有 回答查询时,将权值约束的可达性查询转换为顶点之间的标签交集操作,即只需要计算两个顶点u、v的对应标签Label(u)和Label(v)的交集,找到公共顶点,取较大的权值与约束进行比较,满足条件即返回可达的结论,否则返回不可达。设计代码如下。 算法2 Query输入:q (u,v,C)=输出:TRUE or FALSE 1. if u=v then 2. return TRUE 3. while Label(u)≠Ø and Label(v)≠Ø do 4. node←Label(u)∩Label(v) 5. w←max{(u, node), (v, node)}6. if w≤C then 7. return TRUE 8. break 9. return FALSE 查询算法中,首先判断查询的两个顶点是否是同一个(第1行),如果相同,就返回TRUE(第2行);否则对Label(u)和Label(v)作交集操作(第3行);求得顶点u、v的公共顶点为node以及u和v分别到node路径上的最大值w(第4-5行);如果w≤C满足,则说明顶点u在权值约束下可达顶点v,返回TRUE(第6-8行),否则说明两点之间不可达,返回FALSE(第9行)。 例如给定查询 q=(a,g,≤4),可以根据表 1,Label(a)∩Label(g)={(b,4)},而 4满足≤4,即满足权值约束,说明在约束条件下,顶点a可达顶点g。 其他两种约束形式的查询同理,这里不再赘述。 查询过程主要通过遍历两个标签的个数求解交集,最差情况下,两个顶点的标签都遍历到最后一个标签元组才能回答查询,时间复杂度为O(m+n)(m、n分别为两个被查询顶点的标签个数);最好情况下为 O(m)或者 O(n)(取 m、n中的较小值)。 由本文中的算法均采用 C++语言实现,硬件平台是Intel Core i5,主频是2.4GHz的CPU,RAM为8GB;运行环境为Visual Studio Code。实验通过索引构建时间、索引规模大小以及查询时间作为主要评价指标来比较算法的性能。 实验中所使用的数据由10个的数据集组成,这些数据集被广泛地应用在可达性的相关查询研究中,它们的具体信息如表2所示。由表2可知,|V|表示无向加权图的顶点数量,|E|为边的数量。此外,对于每个数据集,又分别对应生成100万个查询集进行测试,因此算法的查询时间为查询100万个数据的总时间。 表2 数据集统计信息Tab.2 S tatistics of datasets 表3和表4分别给出了现有算法Edge_Index和本文提出的索引构建方法(Degree Index)在所有数据集上的索引规模大小和构建索引时间。 表3 索引大小(MB)Tab.3 Inde x size (MB) 如表3所示,Degree Index方法构建的索引大小明显要小于 Edge_Index方法,在数据集uniprot100m上,前者的索引大小比后者小7.2倍。因为Degree Index方法需要存储的标签个数经剪枝后明显减少,而Edge_Index方法在构建索引时需要存储索引树上所有的结点,要花费|V|2的空间代价,而且对于存储的所有顶点都没有任何剪枝优化效果,所以当数据集的顶点不断扩大,其占用的内存空间也越大,甚至在最后三个数据集上已经超出有限的内存。 由表4可知,Edge_Index方法构建索引的时间要快于 Degree Index,因为前者对索引树只做一次遍历得到最终的序列,而后者需要基于顶点多次访问其余顶点。 表4 索引构建时间(ms)Tab.4 Index time (ms) 本节将通过 100万个随机查询上的查询响应时间对比本文提出的Degree Index方法与Edge_Index方法,具体实验结果见表5。 表5 查询时间(ms)Tab.5 Query time (ms) 实结果表明,Edge_Index方法回答查询的效率较快。因为Degree Index方法查询时需要求解两个顶点标签的交集,在最差情况下需要遍历到最后一个标签才能给出回答,会消耗一定的时间代价,但是总体查询时间相差不大。 针对现有方法解决权值约束可达性查询存在索引规模大、扩展性差的问题,本文基于加权图提出一种优化的 2-hop索引算法。该算法按照顶点的度来确定顶点的处理顺序,然后基于该顺序来构建 2-hop索引;查询处理时,将加权图上的权值约束可达查询转换为基于顶点标签的集合交集操作。实验结果表明,本文提出的方法能有效地降低索引规模,并且在有限内存的环境下高效处理大规模数据图。2.3 查询处理

3 实验与分析
3.1 实验环境
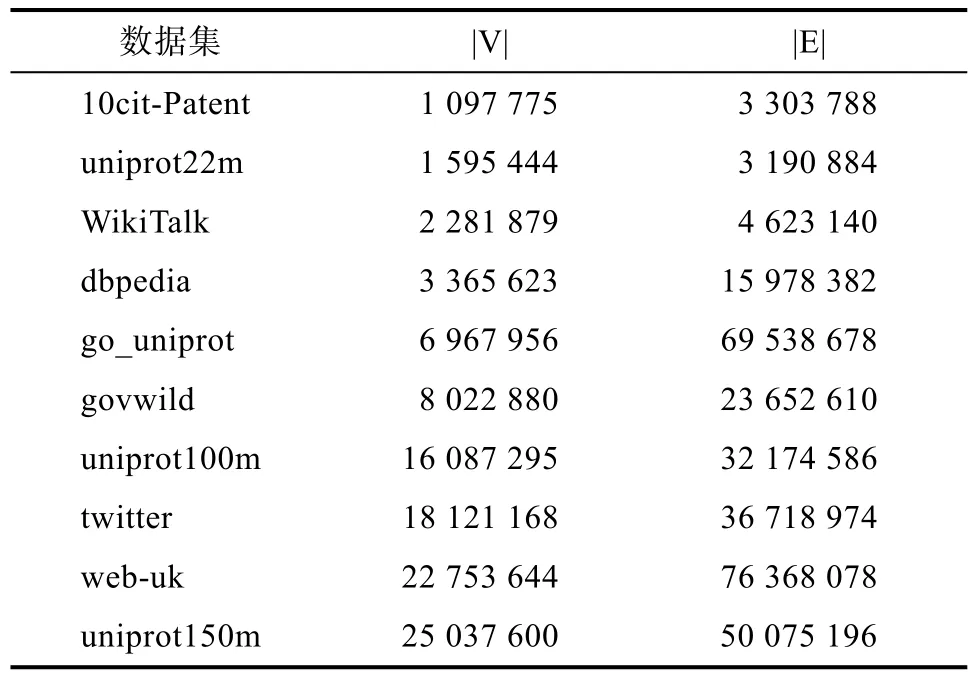
3.2 数据集
3.3 索引大小和时间

3.4 查询时间
4 总结
