设置待行区条件下双环相位信号配时优化模型

杨 震，马健霄，王宝杰

（1.南京林业大学汽车与交通工程学院，南京 210037；2.长安大学运输工程学院，西安 710064）

0 引言

交叉口是城市交通网络的运行瓶颈，对路网的通行能力和交通效率起着决定性的作用。交通工程师往往使用一系列的渠化措施来提高交叉口的通行能力，如进口道拓宽、导流岛、导流线、待行区等，其中待行区渠化是将进口道延伸至停车线之外，使得车辆可在指定时间段进入该延伸区域等候绿灯，主要应用于面积较大、较规范且具有专用或共享左转车道的交叉口，且有左转待转区和直行待行区之分［1］。在设置了左转待转区的交叉口，本方向左转相位应后置于直行相位；而在设置了直行待行区的交叉口，本方向直行相位应后置于相交道路的左转相位［1］。目前关于待行区的研究主要集中在：1）待行区对进口道通行能力、交通运行及交叉口服务水平的影响［2-4］；2）设有待行区车道的排队演化过程分析及建模［5-6］；3）考虑环境效益的待行区多目标优化、评价模型［7-8］；4）基于延迟起动策略的待行区停车次数优化［9-10］；5）左转待转区的安全评价［11-12］。此外，Zhou 等［13］提出了与直左共享车道相适应的左转待转区设计方法，发现该方法能够显著提高直行车道的利用率，而不影响左转车流的效率；Ma 等［14］根据左转车道性质（专用或共享）和左转相位性质（保护或允许）的可能组合，提出了不同的左转待转区设计模式，并针对每一种模式开发了通行能力模型，界定了其应用范围。

在交叉口设有待行区的情况下，车辆可提前一个相位进入到待行区，因此用传统的信号配时方法未必能得到最优方案；但目前较少有文献能够系统性地研究含待行区交叉口的信号配时优化问题。文献［15］中通过调整设置待行区后的车辆起动损失时间，以交叉口平均延误最小为优化目标，建立了信号配时优化的非线性模型；但其研究局限于左转待转区，未能引入更为通用的美国国家电气制造商协会（National Electronic Manufacturers Association，NEMA）标准双环相位，对相位绿灯时间的约束考虑也不充分，因此本文将在NEMA标准双环相位的基础上，提出更为通用的含待行区交叉口信号配时模型及算法。

1 模型建立

1.1 符号定义

为表述方便，设i为交叉口进口方向的全局索引变量，A为交叉口进口方向的集合，且A={1，2，3，4}，其中i=1 表示北进口，其余进口按照顺时针方向依次编号（如图1（a）所示）；设j为交叉口流向的局部索引变量，D为交叉口流向的集合，且D={1，2，3}，对于任意进口方向i，j=1 表示进口方向i的左转流向，其余流向按照顺时针方向依次编号（如图1（b）所示）。全局变量i和局部变量j有式（1）所示的转换关系：

图1 模型中索引变量的定义Fig.1 Definition of index variables in model

式中：Γ(i，j)为流向(i，j)对应的全局变量i值。设k为交叉口进口车道的局部索引变量，Kij为流向(i，j)的车道集合，k=1表示最内侧车道，其余车道按照由内向外的顺序编号。

1.2 相位设计

交叉口相位采用NEMA 在TS-2 标准中制定的双环相位结构，由8 个机动车相位组成，如图2［16］所示。图2 中Φ(i，j)表示流向(i，j)对应的相位，考虑到待行区的运行特性，所有左转相位皆后置于对向的直行相位，图2 中未表示的右转相位则搭接于本方向的直行相位。对于交叉口的过街行人和非机动车，本文假定行人和同方向的机动车一起放行，非机动车则和相应方向的机动车一起放行。

图2 NEMA双环相位结构Fig.2 NEMA dual-ring phase structure

1.3 约束条件

1.3.1 待行区约束条件

在交叉口某一进口道设置待行区后，车辆可提前进入待行区等候绿灯，此效果相当于该车道的绿灯时间在原来基础上增加了车辆在待行区上的行驶时间，因此有：

其中：C表示交叉口信号周期时长（单位：s）；Vijk表示达到饱和流量时，流向(i，j)第k个车道上车辆的排队消散速度（单位：km/h）；λijk表示相位(i，j)第k个车道的绿信比，gij表示相位（i，j）的有效绿灯时间（单位：s）；Wijk表示相位(i，j)第k个车道主停车线至待行区停车线之间的车辆行驶轨迹长度（单位：m），如图3 所示。考虑到车辆在进入左转或直行待行区期间，本方向停车线前的人行横道一般不允许行人通行，因此假定进入待行区的车辆能够占用本方向停车线前的人行横道，在主停车线后方的车辆与待行区停靠的车辆一起组成连续的车队。此外，Vijk具有一定的随机特性，取值不同将导致不同的优化结果，下文实例应用中将对其进行灵敏度分析。

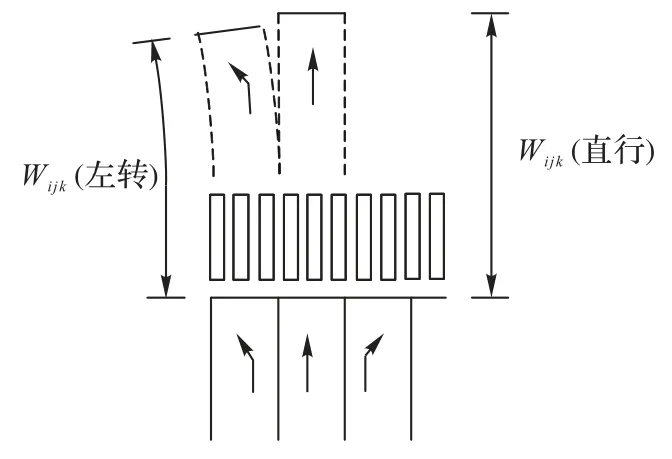
图3 待行区长度示意图Fig.3 Schematic diagram of lengths of waiting area

1.3.2 相位绿灯时间约束条件

为保证行车安全，各相位绿灯时间不宜过短，因此有如下约束条件：

其中：Gij表示相位(i，j)的显示绿灯时间（单位：s）；Gij，min为相位(i，j)的最小显示绿灯时间，在本文中取为10 s。同时，直行相位一般与该相位同方向的行人一起放行，因此其相位时长还必须满足行人过街的需要，因此有如下约束：

其中：Lij为相位(i，j)对应的人行横道长度（单位：m）；Iij为相位(i，j)绿灯间隔时间（单位：s）；vp为行人第15%位步行速度，本文取为1.2 m/s。

1.3.3 环-屏障约束条件

设φij为相位(i，j)的运行时长（单位：s），其值等于相位有效绿灯gij和损失时间lij（单位：s）（或显示绿灯时间Gij和绿灯间隔时间lij）之和，即：

根据NEMA双环相位结构，在每一个屏障内，双环的时长必须相等，因此有：

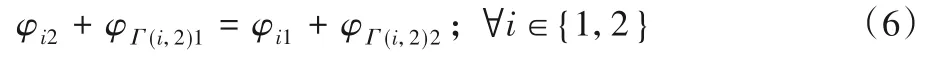
同时，每个环的时长必须等于信号周期，因此有：

1.3.4 延误约束条件

选取延误为主要的效用评价指标，按照《HCM2010》［17］，在设置待行区后，各车道的车辆平均延误可用式（8）～（10）计算：

式中：dijk、dijk1和dijk2分别表示相位(i，j)第k个车道的总延误、均衡相位延误和过饱和附加延误（单位：s）；xijk和Qijk分别表示相位(i，j)第k个车道的饱和度及通行能力（单位：veh/h）；T表示研究时段的长度（单位：h），可取为0.25。其中xijk和Qijk的计算方法为：

式中：yijk和Sijk分别表示相位(i，j)第k个车道的流量比和饱和流量（单位：veh/h）。

1.4 目标函数

模型以交叉口所有车道的加权平均延误最小为目标函数，可表示如下：

其中：qijk是分布到相位(i，j)第k个车道的交通流量（单位：veh/h）。

2 模型求解

以式（1）～（12）为约束条件，式（13）为目标函数，就构成了本文待行区条件下双环相位信号配时优化模型。该模型为非线性整数优化模型，主要的优化变量为各相位有效绿灯时间gij及信号周期C，由于优化变量及约束条件较多，约束条件之间的关联性较强，用传统的解析法难以求解，因此本文设计了如下的遗传算法用于求解此模型。

2.1 编码方式的确定

将双环相位的信号配时方案看作种群中的个体，各相位的有效绿灯时间看作个体的基因片段，基因片段根据索引变量i和j，按照g11，g12，g21，g22，…的顺序排列。每个基因片段采用二进制编码，表示成二进制串(bw1，bw2，…，bwv，…，bwn)，其中bwv表示第w(w=1，2，…，8)个基因片段第v(v=1，2，…，n)位的二进制码，n为二进制串的长度。遗传操作在二进制位串空间上进行，而每个二进制串通过如下方式转换成十进制数：

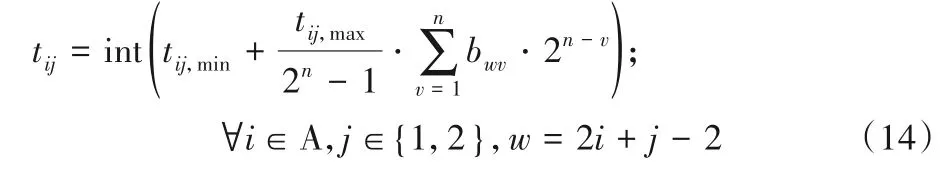
式中：tij为相位(i，j)通过二进制串转换得到的有效绿灯时间；tij，min和tij，max表示遗传操作中相位(i，j)有效绿灯时间的下限和上限值（单位：s）。在得到tij后，考虑到式（6）的屏障约束条件，还需要对其作出一定调整，才能得到满足双环结构的配时方案（即个体的表现型）。设Bi=max(ti2+li2+tΓ(i，2)1+lΓ(i，2)1，ti1+li1+tΓ(i，2)2+lΓ(i，2)2)，则各相位的有效绿灯时间gij可通过式（15）、（16）计算得到：

这样调整以后，某些gij可能会大于tij，max，但不影响遗传算法的执行。

2.2 适应度函数的选取

选取模型目标函数的倒数，即F（x）=1/z为适应度函数，个体的适应值越高，进入选择操作或直接进入下一代的概率就越高。

2.3 选择策略的确定

选取锦标赛算子作为遗传算法的选择策略，在每代种群中随机选取2 个个体，比较其适应值，适应度较高的个体将被选为生成下一代的父体。

2.4 遗传算子的确定

选取单点杂交算子从父代中生成子代，再对生成的子代使用变异算子，即以一定的变异概率将所选个体的位取反。

2.5 遗传控制参数的选取

经过反复多次实验后，本文遗传控制参数按如下方法选取：种群规模取为200，变异概率取为0.2，最大迭代次数取为1 000。为保持解的多样性，每代种群中20%的个体为随机生成的新个体，适应度最高的个体直接进入下一代，其余个体则通过选择策略、杂交算子和变异算子进化得到。

3 实例应用

为验证模型有效性，本文选取南京市太平北路—珠江路交叉口进行待行区条件下双环相位的信号配时优化。通过在线电子地图获取该交叉口的几何形态及关键几何数据，通过实地观测获取交叉口高峰时期的交通流量，如图4 及表1 所示。从表1 中可以看出，该交叉口的东西方向为重交通流方向。此外，为分析本文模型中车辆排队消散速度Vijk的灵敏度，对该交叉口的排队消散速度进行了调查，得到左转车辆的第15%位及85%位车速分别为18.9 km/h 和23.4 km/h，最小速度和最大速度分别为16.9 km/h 和26.4 km/h，直行车辆的第15%位及85%位车速分别为23.0 km/h 和29.2 km/h，最小速度和最大速度分别为18.8 km/h和33.1 km/h。

表1 实例交叉口交通流量数据及待行区长度Tab.1 Traffic flow volume data and waiting area length of example intersection

图4 实例交叉口几何形态Fig.4 Geometric shape of example intersection

根据交叉口几何形态及交通流量数据，首先使用美国Trafficware 公司的Synchro 软件，为该交叉口设计一组常规的双环相位配时方案。配时过程中各流向的高峰小时系数取为0.8，各相位起动停车损失时间取为3 s，各相位的绿灯间隔时间按照式（17）计算：

式中：dij为相位(i，j)各车道停车线到冲突点的最大距离（单位：m）；uij为相位(i，j)排队尾车的行驶速度（单位：km/h）；ts为车辆制动时间（单位：s），本文中取为1.5 s。当计算得到Iij≤3 s时，设置黄灯时间3 s；当Iij＞3 s时，设置黄灯时间为3 s，其余时间配以全红时间［18］。在Python 3.8 中对本文设计的遗传算法进行编程，分别在以下四种情形中执行算法：

情形1 交叉口仅设置左转待转区，排队消散速度取为最小车速；

情形2 交叉口仅设置左转待转区，排队消散速度取为最大车速；

情形3 交叉口同时设置左转、直行待行区，排队消散速度取为最小车速；

情形4 交叉口同时设置左转、直行待行区，排队消散速度取为最大车速。

算法执行过程中，取各相位的tij，max为100 s，tij，min则根据式（3）和式（4）确定，由于各相位gij的可能取值数目介于26和27之间，因此取二进制串长度n=7，最终得到每种情形的配时方案如图5所示，延误状况如表2所示。

表2 实例交叉口各情形延误状况Tab.2 Delay of different cases at example intersection

图5 实例交叉口各情形配时方案Fig.5 Signal timing schemes of different cases for example intersection

从图5和表2中可以看出，本文模型在四种情形中均得到了比Synchro 软件周期更短、平均延误更低的配时方案，其中当交叉口仅设置左转待转区（情形1和2）时，随着排队消散速度取值的不同，延误降低幅度在12.9%～17.4%；当交叉口同时设置左转、直行待行区（情形3 和4）时，延误降低幅度在17.5%～25.5%。具体到每个相位来看，重交通流方向的各个相位（Φ2，1、Φ2，2、Φ4，1和Φ4，2）及北进口的直行相位（Φ2，1）的关键车道延误有了显著降低，而其他相位下降不显著或反而升高，说明本文模型主要优化了重交通流相位的行车效率。此外，虽然排队消散速度的不同取值导致了不同的平均延误，但由图5可知，情形1和情形2的配时方案完全相同，情形3和情形4 的部分相位时长有1 s 的差别，配时方案几乎相同，说明本文模型对车辆排队消散速度如何取值并不敏感，具有良好的可操作性。

4 结语

本文在交叉口设置待行区的条件下，将交叉口相位设为通用的NEMA 双环相位，将待行区的效果等效为车道绿信比的增加，建立了双环相位信号配时优化模型；然后考虑相位结构中的环-屏障约束，设计了用于求解模型的遗传算法，并将模型和算法应用于实例交叉口。结果表明，与Synchro软件得出的方案相比，本文模型能够显著降低设有待行区交叉口的车辆平均延误，并且在排队消散速度取为最小速度及最大速度时，模型能够得出相同的信号配时方案，表明其对排队消散速度的取值不敏感，具有良好的可操作性。下一步的研究可考虑设置了直左、直右等共享车道的交叉口，进一步提高模型的通用性。