基于热流固多场耦合的埋地输油管道地震响应

2021-07-30滕振超刘凯琪滕云超赵誉翔

东北石油大学学报 2021年3期

滕振超，刘凯琪，滕云超，赵誉翔，计静

(1. 东北石油大学土木建筑工程学院，黑龙江大庆 163318； 2. 东北石油大学黑龙江省高校防灾减灾工程与防护工程重点实验室，黑龙江大庆 163318； 3. 中国地震局工程力学研究所地震工程与工程振动重点实验室，黑龙江哈尔滨 150086 )

0 引言

中国输油气管线的铺设覆盖范围广，受地震作用影响，极易引发管线破坏和泄漏。中国埋地输油管道的抗震设计并不完善，规范中管道受力模型主要参考反应位移法[1]，主要模拟地震作用下管土之间的相互作用力[2]，未考虑管体与流体之间的耦合作用。管体在地震激励下振动，振动影响管内流体，流体变化影响管体动力特性，称为流固耦合效应。考虑流固耦合时，计算结果更精确，因此将热流固耦合理论应用于埋地输油管道具有工程实际意义。

ARRIS S T等[3]对输液管道流固耦合受力进行分析，拓展经典水锤理论，考虑流体与结构耦合，建立流固耦合4-方程模型；WALKER J S等[4]提出流固耦合6-方程模型，说明管路的径向运动，但忽略泊松耦合影响；在AKIRA M等[5]的流固耦合4-方程模型基础上，BROWN F T等[6]考虑管线泊松耦合和Bourdon耦合影响，并验证模型的正确性；张挺等[7]应用有限积分法，分别配合隐式欧拉法和拉普拉斯数值反演法，研究瞬时关阀时输流直管轴向耦合振动响应特性；李森[8]提出适合于变径圆管结构的双向流固耦合模型；陈坚红等[9]采用C++语言编制充流管道单向流固耦合数值模拟程序，模拟管内流体压力分布及流体压力数据，导入管体结构进行管道应力计算；周知进等[10]利用有限元方法，分析不同曲率管道的流固耦合特性，并研究流固耦合作用对不同曲率管道位置等效应力影响；梁军等[11]通过ADINA软件建立流固耦合有限元模型，得到流固耦合下管体抗震性和管内介质流速等参数对管道的损伤。对埋地输油管道在地震作用下的流固耦合动力学问题研究较少。笔者将热流固耦合动力学运用到埋地输油管道的地震响应中，利用ANSYS Workbench建立埋地输油管道热流固耦合模型，分析热流固耦合下输油管道在地震响应中的变形和应力，建立土—管—液三维有限元模型，考虑多物理场对管道受力性能影响，研究埋地输油管道在严寒环境下的安全和力学行为特性，为埋地输油管道建设提供技术支持。

1 流固耦合方程

1.1 温度场方程

根据热力学第二定律，热量传递是由温差导致的，热量传递包括对流、传导和辐射[12]。严寒地区地表温度较低，土体内部及管输液体温度相对较高，温差通过热传导方式传递。

管道和土体传热微分方程分别为

(1)

(2)

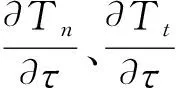
1.2 管—液耦合方程

埋地输液管道由管道单元和液体单元组成，管—液耦合发生在两相交界面上。在分析流固耦合时，计算域包括固体域和流体域，流体单元上的力作用在固体单元上，固体变形又反作用在流体单元上[13]。

运动学和动力学条件分别为

df=ds,

(3)

nTf=nTs,

(4)

式(3-4)中：f为管输介质；s为固体管道；df为流体位移；ds为地下管线位移；Tf为流体压力；Ts为管道应力。式(3-4)适用于流固耦合交界面。

流固耦合有限元方程为

(5)

式中：Ff为流体有限元方程；Fs为地下管线有限元方程；Xf为流体求解矢量；Xs为管道求解矢量；ds(Xs)为管线节点；df(Xf)为流体节点。当流体方程和埋地管道方程耦合时，Ff[Xf,0]=0和Fs[Xf,0]=0。

1.3 地震作用下管—液耦合方程

波动法为分析输油管道振动的有效方法。由流固耦合“四方程模型”[14]可得到流体单元和管道单元方程。管道单元受力见图1，其中，Fy为流体单元轴向应力，ρp为压力管道密度，Ap为压力管道截面面积，uy为管道轴向位移。

流体和管道方程分别为

(6)

(7)

联立式(6)与式(7)得输油管道轴向应力σy(y)为

(8)

基于式(1)、(2)、(5)、(8)对埋地输油管道建模，可分析流固耦合及温度场下的埋地输油管道地震响应。

2 有限元分析

2.1 管—油流固耦合模型

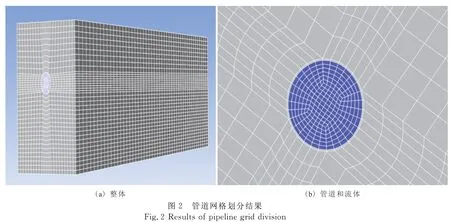
以中俄输油管道大庆段为例，建立有限元模型。取土体尺寸为40 m×5 m×5 m，土体为粉质黏土，管道长度为40 m，通长布置，建立管—油流固耦合模型。模型由液相和固相两部分组成，固液两相交界耦合面包含管道内壁面和液体外壁面。根据管道尺寸，建立管道固体区域，采用ANSYS Workbench中的Fill功能对管道填充，生成流体区域，而后对流固耦合面划分。选择研究对象为 DN850直管道，长度为40 m，管道外径为864 mm，壁厚为16 mm。

2.2 管道网格

管道网格划分采用Soild185六面体8节点单元，最小网格尺寸为200 mm，管道、土体及流体网格划分见图2；考虑管道及流体的重力影响，重力加速度取g=9.8 m/s2，方向取竖直向下。

2.3 流体动网格模型

考虑管道受地震作用影响，流体单元受管道震动而造成收缩或膨胀。此外，固体面的计算结果传递至流体面时，流体单元划分也需要调整，出现流体网格移动问题。为使结果更精确，在推导数学模型时，将Euler坐标下的N-S方程映射到任意拉格朗日—欧拉(Arbitrary Lagrange-Euler, ALE)坐标中解决网格移动问题。流体域用Euler单元，固体域用Lagrange单元，在统一ALE坐标系下求解，使流体域与固体域的交界面随固体域一起变形。

在流固耦合分析中，流体域网格划分影响结果的收敛性。为避免结果不收敛和畸变性，改用四面体单元对流体网格划分，在ICEM[15]里采用弹性光顺法和局部网格重构法求解网格移动问题。

2.4 材料参数

固体域包括土体及管道，土体采用粉质黏土，管道采用结构钢，土体材料属性：密度为1.6 g·cm-3，比热容为1 450 J/(kg·K)，导热系数为1.69 W/(m·K)。流体域采用石油，密度为960 kg/m3。管材结构钢物理参数见表1。

表1 管材结构钢物理参数

2.5 模型边界条件

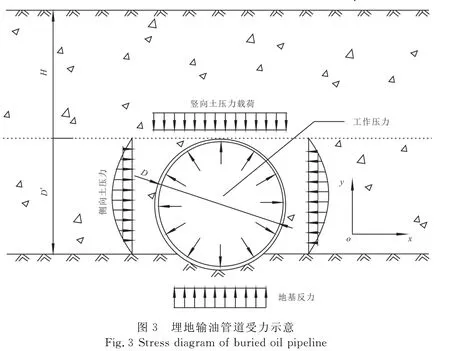
埋地输油管道受力见图3，其中，H为管道覆土厚度，D*为管顶至管道底面距离。管道埋深为2 m，通长布置的管道两端面采用固定端约束，模拟计算范围等于管道长度。考虑管道与管中液体自重影响，静载下，管道受左右两侧土压力相互平衡，地基反力与竖向压力载荷、管道及管内流体自重、地基承载力有关，将管道上方土压力等效为均布荷载：

F=CγHD,

(9)

式中：F为等效竖向土压力荷载；C为土压力因子；γ为回填土重力密度,γ=ρg；D为管道外径。

对管中流体部分设置标准为k-ε湍流模型，忽略流体与管壁的热量交换，定义流速入口端面和流速出口端面与管端平齐，为自由平面，不设置约束；出入口处，流体速度取绝对速度，为10 m/s，方向垂直端面，并取湍流强度为5%，湍流黏度比为10。

当输油管工作时，管内为压力流，工作压力取8 MPa；对流固耦合面设置流体经过管壁不产生侧移，耦合面粗糙度因子取0.5。

2.6 热流固耦合模型求解

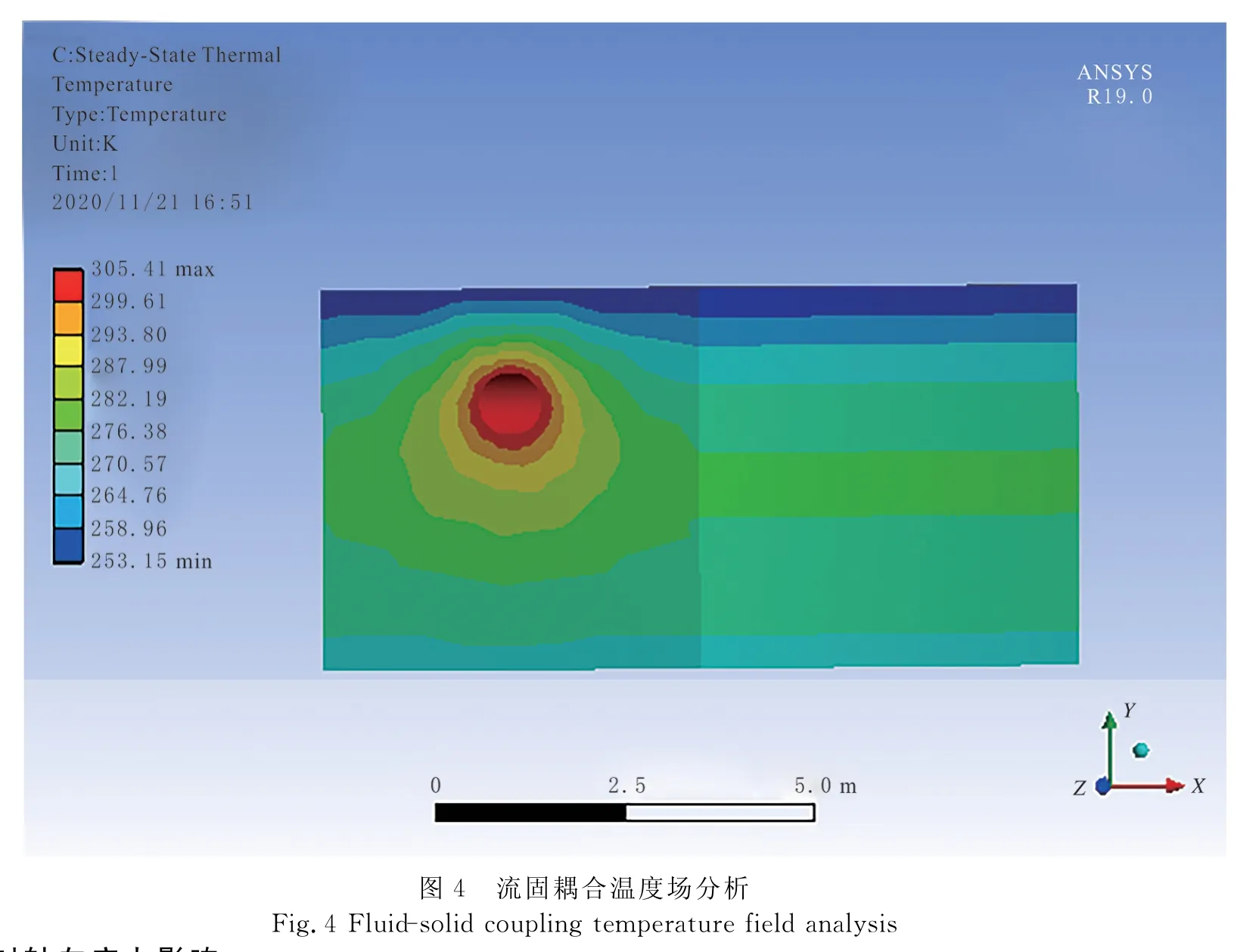
管道与流体的耦合方程见式(5)。采用牛顿—拉夫森迭代法，在每个时间步上将流体域的计算结果加至固体域上。地表温度设置为253.15 K，5 m深处土层温度为268.15 K。热流固耦合模型求解结果见图4。

冻土区埋地管道周围土层温度场的分布呈现似椭圆形，距离管道越近，温度线越密集，管道上部温度线比下部温度线密集。这是因为严寒地区地表温度低，油温高，使上层土体温度与油温度相差较大，所以液油的热量向上部传导。土体温度由上而下逐渐增大，管道周围的温度场变小，保持液油温度为31.5 ℃，埋地管道对油的保温具有明显优势。

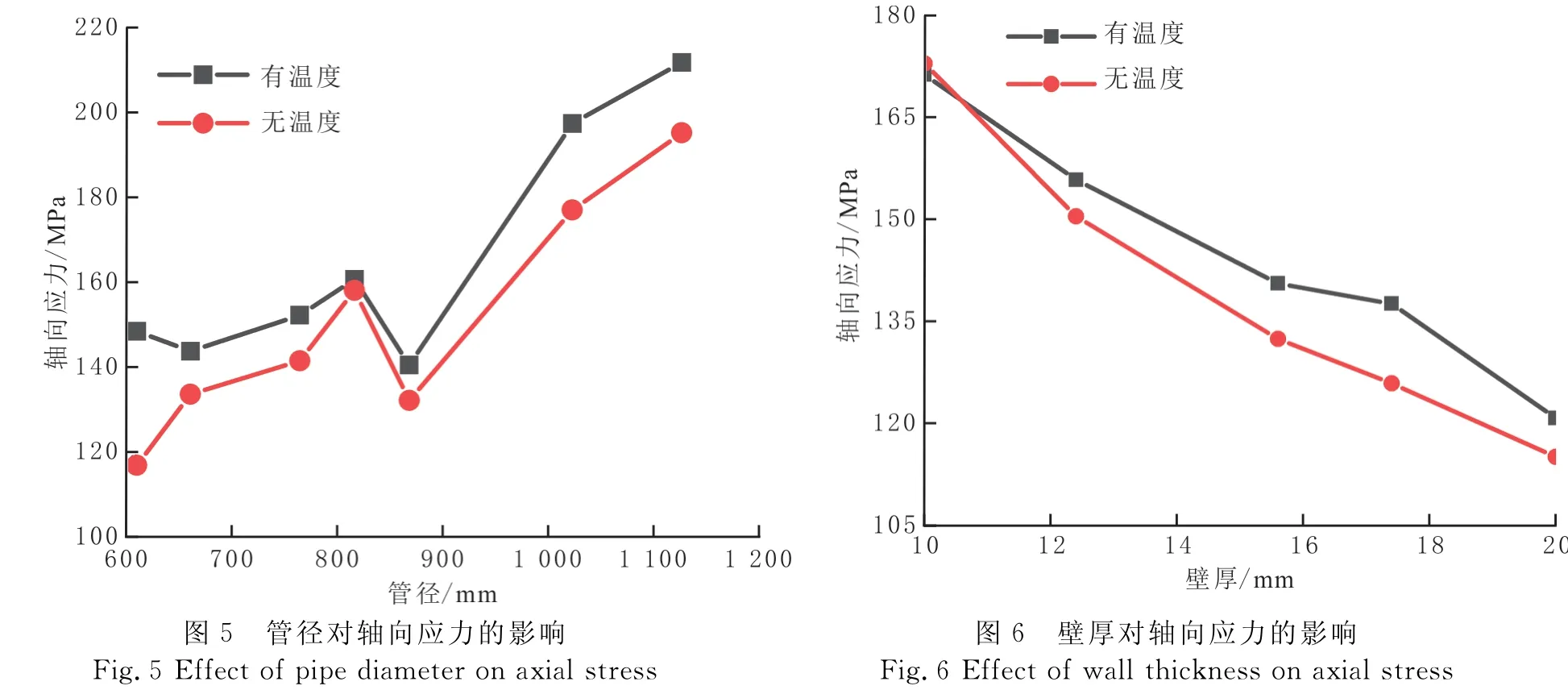
2.7 管径对轴向应力影响

采用管长为40 m，壁厚为15.6 mm，液体压力为8 MPa，埋深为2 m，取610、660、762、813、864、1 016、1 118 mm 7种管径分别进行流固耦合求解。管径对轴向应力的影响见图5。

由图5可知，当管道壁厚、埋置深度和液体压力一定时，随管道直径的增加，轴向应力逐渐增大，可见管道直径对管道轴向应力影响较大；对比有温度场与无温度场两种工况，有温度场下的轴向应力更大，说明温度场对轴向应力有影响。

2.8 壁厚对轴向应力影响

采用管长为40 m、管径为864 mm、液体压力为8 MPa、埋深为2 m，取10.0、12.4、15.6、17.4、20.0 mm 5种壁厚分别进行流固耦合求解。壁厚对轴向应力的影响见图6。

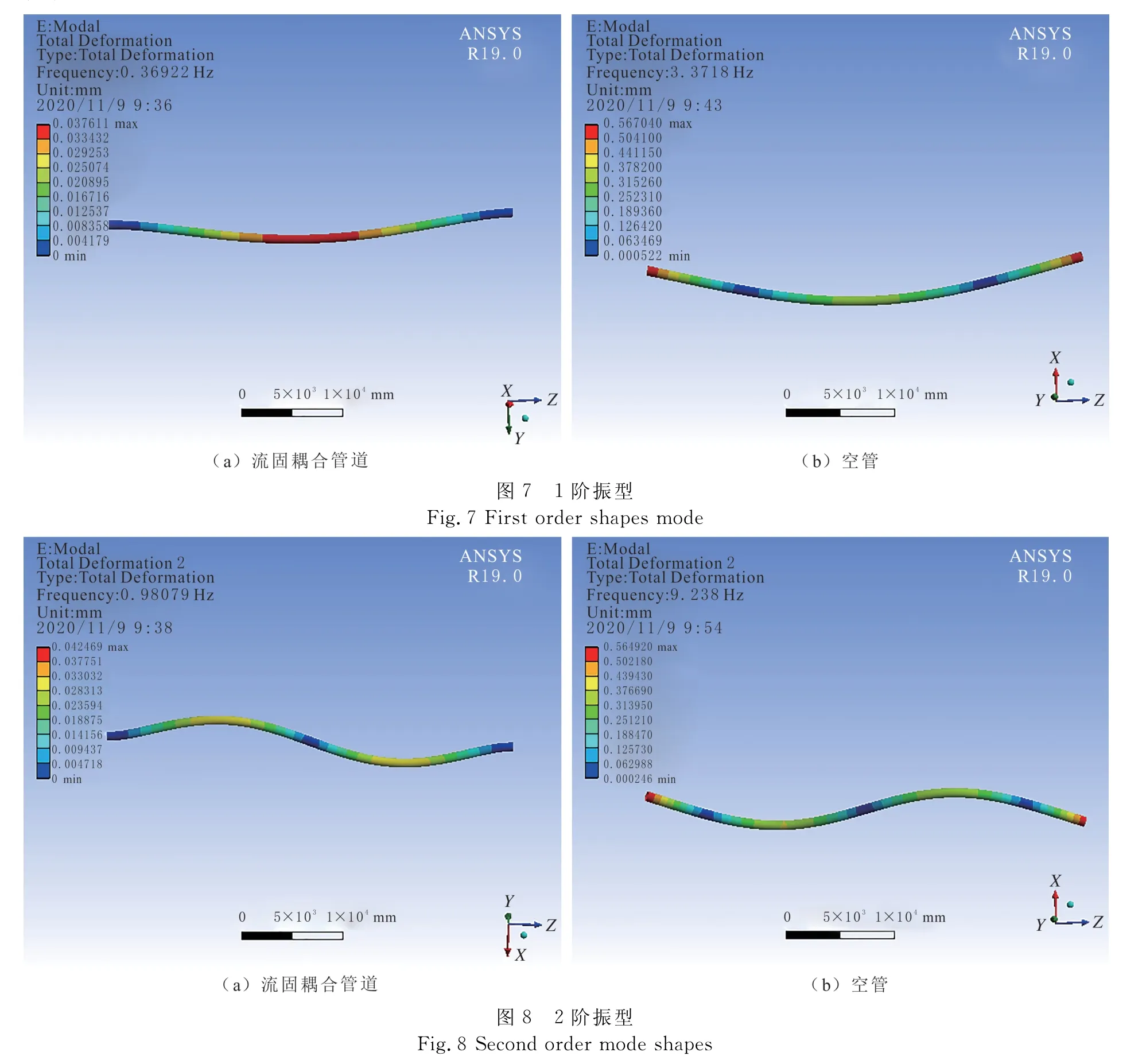
由图6可知，当管道直径、埋置深度和液体压力一定时，随管道壁厚的增加，轴向应力逐渐减小，可见管道壁厚对管道轴向应力影响较大。对比有温度场与无温度场两种工况，温度场下的轴向应力值更大。

2.9 流固耦合下管道模态

研究流固耦合[16]因素影响下管道的振动特性，分析空管的固有频率和自振周期。流固耦合下管道模态分析见表2。

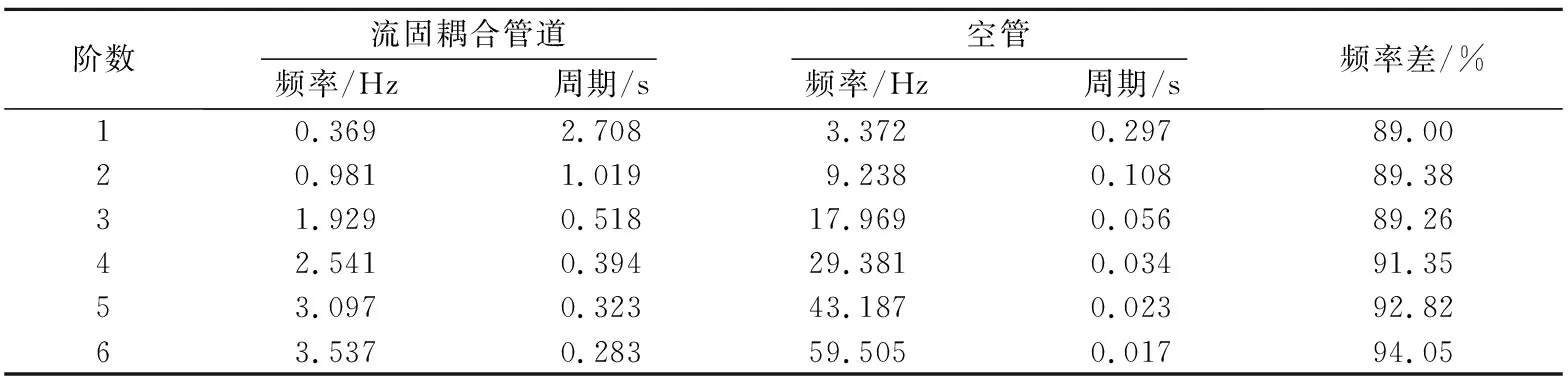
表2 流固耦合下模态分析结果

由固有频率计算公式[17]可知，固有频率主要取决于质量矩阵和刚度矩阵。由表2可知，流固耦合下管道的基频为0.369 Hz,空管基频为3.372 Hz，空管和流固耦合管道的基频不高，第1阶空管频率比流固耦合管道频率高出89%。从第2阶开始，两者频率出现较大增幅，变化相似且呈增长趋势。从第2阶到第6阶，流固耦合下管道的固有频率降至89%以上，说明液体对管道频率影响明显。第1阶到第5阶振型见图7-11。

3 时程响应分析

3.1 地震动力施加

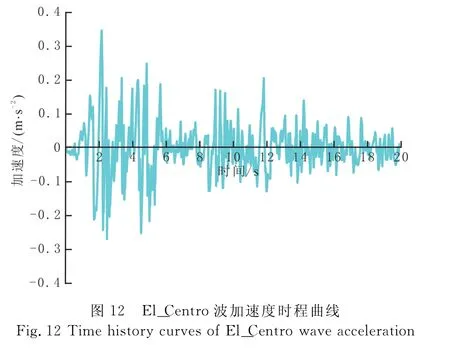
以El_Centro南北波型为例，取前20 s计算时间，作为输油管道地震动力荷载，取地震加速度为0.35 m/s2。El_Centro波加速度时程曲线见图12。

在ANSYS Workbench中利用Transient Structural模块施加地震波。将地震动力施加管道上，时间设置为20 s，以0.02 s为1个时间步长，输入每个时间点对应的地震加速度，共输入1 000组数据，模拟输油管道在地震波作用下的振动情况。地震波的传播方向设为沿管道的横向(X)、竖向(Y)和轴向(Z)三个方向输入。

3.2 单向一致激励

以El_Centro波分别沿管道的横向(X)、竖向(Y)和轴向(Z)三个方向输入地震动加速度时程,分析管道位移、应力。

3.2.1 管道位移影响

考虑流固耦合场与温度场两种工况响应，对管道与土块同时施加X、Y、Z三个方向激励。管道不同时刻对应X、Y、Z三个方向位移时程响应曲线见图13。

由图13(a)可知，X、Y、Z向激励下，对X向位移影响峰值分别为67.879、49.791、18.366 mm，出现时间分别为16.84、5.78、1.34 s。因此，X向激励对管道X向位移影响最大。由图13(b)可知，Y向位移在X、Y、Z向激励下最大值分别为12.494、49.997、7.731 mm，峰值出现时间分别为15.44、5.78、1.32 s。因此，Y向激励对Y向位移影响最严重。由图13(c)可知，X、Y、Z向激励对Z向位移影响峰值分别为10.662、12.507、6.115 mm,峰值出现时间分别为11.64、6.88、4.56 s。综合分析可知，X向激励对X向位移影响最大，Z向激励对Z向位移影响最小，因此，可考虑在X向上多加约束，限制管道在X向的变形。

3.2.2 管道轴向应力和变形影响

考虑流固耦合场与温度场两种工况影响，对管道与土块同时施加X、Y、Z方向激励。管道不同时刻轴向应力与管体变形时程响应曲线见图14。

由图14(a)可知，X、Y、Z向激励下，管道轴向应力分别为208.78、177.49、127.41 MPa,出现时间分别为11.44、6.92、3.78 s，X向激励比Y向激励高出14.9%，X向激励比Z向激励高出38.9%。因此X向激励对管体的轴向应力影响最大。

由图14(b)可知，X、Y、Z向激励引起管道变形最大值为68.263、50.871、19.791 mm，出现时间分别为18.86、5.80、1.32 s。因此，X向激励引起的峰值变形最大。

综合分析可知，X向激励对管体变形影响最严重。

3.3 热流固耦合影响

以El_Centro波沿垂直管轴Y向输入一致激励，分析流固耦合场下相应的位移、应力。

3.3.1 不同方向位移响应

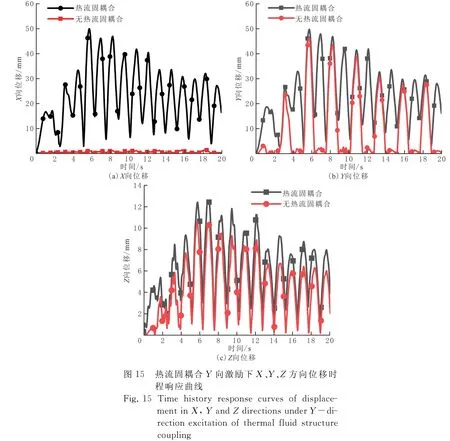
考虑热流固耦合与无热流固耦合两种工况影响，管道受Y向激励不同时刻的X、Y、Z三个方向位移时程曲线见图15。

由图15(a)可知，热流固耦合与无热流固耦合下X向位移峰值分别为49.791、1.311 mm，出现时间分别为5.78、18.32 s；由图15(b)可知，热流固耦合与无热流固耦合下Y向位移峰值分别为49.997、46.674 mm，出现时间分别为5.78、5.92 s；由图15(c)可知，热流固耦合与无热热流固耦合下Z向位移峰值分别为12.507、10.625 mm，出现时间分别为6.88、5.76 s。对比热流固耦合下的X、Y、Z三个方向的峰值位移，Y向49.997 mm>X向49.791 mm>Z向12.507 mm，Y向激励下热流固耦合对Y向位移的影响最大。

3.3.2 轴向应力与管体变形响应

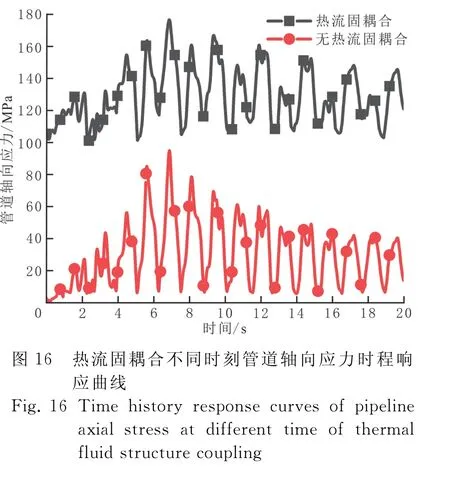
考虑热流固耦合与无热流固耦合两种工况影响，管道受Y向激励不同时刻管道轴向应力与管体变形时程曲线见图16。

由图16可知，热流固耦合下的管道轴向应力峰值为177.490 MPa,出现时间为6.92 s；无热流固耦合下的管道轴向应力峰值为95.766 MPa，出现时间为6.92 s，二者差值率为46%。因此，Y向激励下热流固耦合对管道轴向应力的影响更大。

综上分析可知，在进行埋地输油管道轴向应力、位移分析及抗震设计时必须考虑热流固耦合的影响。