基于社区优化的深度网络嵌入方法
2021-07-30李亚芳冯韦玮祖宝开康玉健
李亚芳,梁 烨,冯韦玮,祖宝开,康玉健
(北京工业大学信息学部,北京 100124)
0 引言
网络已成为最常见的信息载体和表示形式,在我们日常生活与工作中无处不在,如社交网络、论文合作者网络、通信网络以及生物网络等。文献[1]指出在社交网络已成为人工智能应用焦点的大背景下,对网络数据进行研究与分析,已经受到社会各界的广泛关注,在用户画像、内容推荐、舆情监测、生物分子功能团识别等众多领域具有潜在应用价值。
然而,随着互联网技术以及大数据的蓬勃发展,以微博、微信、Twitter 和Facebook 为代表的社交网络进入亿级节点时代,不仅网络规模不断扩大、链接关系更加复杂,还存在缺失数据和噪声信息,这为大规模网络的相关研究提出了更新、更大的挑战。对于这类大规模稀疏复杂网络,文献[2]中指出,传统网络分析方法将网络表示为高维、稀疏的邻接矩阵,存在如下问题:计算复杂度高;节点通过边关联,难以并行化;难以直接应用机器学习方法,对于大规模网络的高维、稀疏向量,已有的统计学习方法会花费更多的运行时间和计算空间,使得许多先进的研究成果无法直接应用到现实的网络环境中。
网络嵌入方法是解决传统方法缺陷的有效方式,在保留结构信息的前提下,为网络中的每个节点学习一个低维、稠密的连续特征向量表示[3-4]。通过将网络数据表示成一种高效合理的形式,不仅有助于更好理解节点之间的语义关联,而且能够有效解决大规模网络中的稀疏性,也可作为经典机器学习模型的输入,采用已经成熟的模型和方法将其运用于后续节点分类、社区发现、链接预测以及可视化等网络分析任务中,对解决现实网络中的实际应用问题具有重要意义,如:通过节点分类构建用户推荐系统;通过社区发现进行舆情监测;通过链路预测推测蛋白质之间可能存在的相互作用关系以推动疾病的治疗。
近年来,针对网络结构的网络嵌入方法被相继提出,大致可分为基于因子分解的方法[5-13]与基于神经网络的表示方法[14-20]。基于因子分解的方法首先构造关系矩阵,通常为邻接矩阵、Laplacian 矩阵、节点转移概率矩阵或其他相似度矩阵,通过对关系矩阵的分解得到节点的低维向量表示。该类方法可进一步分为:1)特征值分解方法(特征向量表示方法),如局部线性表示(Locally Linear Embedding,LLE)[5]、拉普拉斯特征表示(Laplacian Eigenmaps,LE)[6]、结构保持方法(Structure Preserving Embedding,SPE)[7]。2)矩阵分解方法。主要包括图分解方法(Graph Factorization,GF)[8]、Graph Representation(GraRep)[9]、高阶近邻保持嵌入方法(High-Order Proximity Preserved Embedding,HOPE)[10]、模块化非负矩阵分解方法(Modularized Nonnegative Matrix Factorization,M-NMF)[11]、考虑网络社区结构的非负矩阵分解方法(Network Embedding with Community Structural information,NECS)[12]以及网络嵌入更新方法(Network Embedding Update,NEU)[13]。GraRep 通过构建k阶相似度矩阵,往往能得到较好的效果,但算法的计算复杂度更高。NEU 则采用相似性方法提高基于高阶相似度矩阵进行节点表示的效率。M-NMF 通过融合模块度进行非负矩阵分解,将社团结构信息融入网络表示学习中。类似地,NECS 基于随机块模型,将节点高阶的特征矩阵和社区结构联合分解,得到保持网络社区结构的低维表示。基于因子分解的方法构建的关系矩阵包括高阶节点链接信息时,能够显著提升节点表示的效果;但计算和存储效率相对较低,难以扩展到大规模网络。而且基于因子分解方法只关注节点间线性结构关系是不够的,因为网络的形成是非常复杂的过程,节点间常具有非线性复杂结构关系,因此,网络研究者利用神经网络建模节点表示之间的非线性关系。
DeepWalk 方法[14]是第一个采用神经网络进行网络表示学习的方法,通过随机游走得到网络结构的线性序列,进一步采用训练词向量的神经网络模型SkipGram 进行网络中节点的表示学习。在DeepWalk 的基础上,人们相继提出了node2vec[15]、层次网络表示方法(Hierarchical Representation Learning for Networks,HARP)[16]、判别深度随机游走模型(Discriminative Deep Random Walk,DDRW)[17]以及基于边采样的网络表示学习模型(Network Embedding model based on Edge Sampling,NEES)[18]。DeepWalk 及其扩展方法通过某种随机游走策略自动地抽样网络中节点的路径,然后通过神经网络模型得到节点的表示,但这类方法属于浅层神经网络方法,难以充分捕捉现实世界复杂网络中节点间的高度非线性关系。进而,Wang 等[19]提出基于深度自编码节点表示方法(Structural Deep Network Embedding,SDNE),通过综合考虑网络拓扑结构的一阶和二阶相似度,取得了较好的节点表示性能。深度神经网络表示方法(Deep Neural Networks for Graph Representation,DNGR)[20]构建节点间PPMI(Positive Pointwise Mutual Information)关联矩阵,通过深层降噪自编码模型学习节点的低维向量表示。基于深度学习的网络表示方法具有更强的节点表示能力,不仅能够学习节点间复杂的非线性关系,而且可通过高效优化方法求解模型参数。
节点低维特征表示的学习,为大规模网络的分析和处理提供了一条可行解决思路。但已有方法得到节点低维特征向量后,需要将其作为其他应用(节点分类、社区发现、链接预测、可视化等)的输入来进一步分析,采用的是两步走策略;缺少针对具体应用来设计模型,因为不同的应用场景对学习特征的选择通常有不同的要求。网络社团结构是网络分析的主要任务之一,也是复杂网络的重要结构特性。在网络嵌入过程中,将网络的社团结构融入节点嵌入表示过程中,也能够从全局的角度揭示节点之间的隐含关系,有助于提高节点嵌入表示的质量。因此,本文针对网络节点聚类(社区发现)的应用,基于深度神经网络的自动编码器模型SDNE,结合网络的局部和全局拓扑结构特性以及深度嵌入聚类(Deep Embedding Clustering,DEC)算法[21],提出节点低维表示和社区结构优化的深度网络嵌入模型CADNE(Community-Aware Deep Network Embedding)。该模型同时学习节点的低维特征表示和节点所属社区的指示向量,使节点的低维表示不仅保持原始网络结构中的近邻特性,而且保持原始拓扑空间的社区结构。本文主要工作如下:
1)基于深度自编码模型提出一种网络聚类结构优化的深度网络嵌入模型CADNE,该方法能够同时学习网络节点拓扑链接以及节点社区结构的非线性关系,得到节点在低维特征空间的向量表示;
2)给出了CADNE模型的框架以及参数的求解方法;
3)与已有网络嵌入方法在经典数据集进行实验对比,在聚类、分类、链接预测以及可视化等不同应用上,验证了提出CADNE的有效性。
1 深度优化的深度网络嵌入CADNE
1.1 基本定义
定义1 网络(network)。网络可描述为G=(V,E),V={v1,v2,…,vn}表示网络中n个节点组成的集合,E表示节点间边的集合。每条边e∈E是一对包含权重Aij的有序节点对e=(vi,vj),如果节点vi和vj间不存在链接,则Aij=0;若存在链接,对于无权网络Aij=1,对于有权网络Aij>0。
定义2 一阶相似性(first-order proximity)。描述任意两个节点之间的局部结构相似度,如果两个节点间存在链接,其一阶相似性Aij>0,否则为0。
一阶近邻描述网络中存在直接链接的节点对之间的相似度,只关注两个节点对之间是否存在直接的链接。然而,现实网络的链接关系往往非常稀疏,而且存在很多非常相似的节点对之间并没有直接链接关系,因此,引入二阶相似性作为补充以描述全局网络结构的相似性。
定义3 二阶相似性(second-order proximity)。描述任意两个节点近邻结构的相似性,对于节点vi和vj,Ai={Ai1,Ai2,…,Ain}和Aj={Aj1,Aj2,…,Ajn}中元素值分别表示两个节点与网络中其他节点的一阶相似性,则节点vi和vj的二阶相似性为向量Ai和Aj的相似度。
可见,如果两个节点共有的邻居节点越多,其二阶相似性越大,这两个节点越相似;若两个节点间不存在共同的邻居链接,其二阶相似度为0。通过二阶相似性可度量网络中未存在直接链接关系的节点对之间的相似度,度量网络节点的全局结构相似度。本文同时考虑节点间的一阶相似性和二阶相似性,对网络中的节点进行映射表示。
定义4 网络嵌入(network embedding)。对网络G=(V,E),学习映射函数f:V→Rd将每个节点映射为d(d<n)维特征空间的向量。
1.2 CADNE模型框架
给定无向网络G=(V,E),节点间的链接关系可用邻接矩阵表示A=[A1,A2,…,An]描述,可见,原始网络拓扑结构空间中,每个节点通过n维向量进行表示。本文提出基于深度嵌入聚类进行社区优化的深度网络表示模型,学习节点在d维低维特征空间的表示,同时得到节点的社区划分,整个模型框架如图1所示。

图1 CADNE模型框架Fig.1 Framework of CADNE model
该模型主要由两部分组成:第一部分是深度自编码模型通过非线性激活函数进行参数训练,将节点映射为易于计算的低维、稠密向量表示,以保持原始网络结构中节点间高度非线性关系,在映射过程中,保持网络节点一阶相似性(局部)及二阶相似性(全局)的拓扑特性;第二部分是基于DEC 模型,利用节点聚类结构对节点低维表示进一步优化,使得节点低维表示过程中仍保持节点聚集特性,通过交替迭代更新深度自编码模型的编码过程以及节点聚类,得到社区结构优化的节点低维表示。
1.3 保持网络拓扑结构
为了使低维表示后的节点在新的特征空间中仍保持原网络拓扑结构中的近邻特性,综合考虑节点间的一阶相似性以及二阶相似性,采用深度自动编码实现节点稀疏表示的降维。深度自编码器包括编码和解码两部分,编码过程通过多层非线性函数将输入数据映射到低维特征空间;解码过程也通过多层非线性函数将低维特征空间映射到重建后的输出表示。
设xi表示根据网络结构得到的模型输入,如果输入为邻接矩阵,则xi=Ai,每个元素描述节点vi与网络中其他节点的链接关系,即节点的全局链接结构特征。通过将邻居矩阵作为输入,得到低维表示后,在解码阶段的网络重建过程中,使节点在原始拓扑结构中具有相似近邻结构特征节点的低维表示也尽可能相似。假设深度自动编码网络有K层,则每层的隐含表示为:

通过编码器逐层编码降维,得到最深层的zi为节点的低维向量表示,通过逆向解码得到自动编码网络的输出:
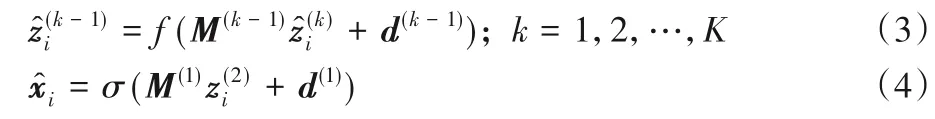
其中:σ(x)、f(x)为非线性的激活函数;θenc={W,b},θdec={M,d}是待学习的编码器和解码器的模型参数。目标是根据新的节点低维表示zi,最小化输入xi和输出的重构误差,通过最小化编码器输入和解码器输出,使得节点近邻结构越相近(二阶相似度越高)的节点对,具有相似的低维向量表示,因此保持网络二阶相似性的目标函数为:

然而,现实网络中链接非常稀疏,只有极少量的边被观测到,因此邻接矩阵中零元素个数远多于非零元素的数目。如果直接使用邻接矩阵作为模型的输入,过多的零元素将会影响原始网络的低维表示以及重建过程,通过最小化重构误差会使得节点的重建表示倾向于重建很多零元素。因此,在网络低维表示和重建过程中,重点关注邻接矩阵中的非零元素,定义二阶相似性目标损失函数L2nd为:

其中:⊙是哈达玛积;Bi=如果邻接矩阵元素Aij=0,Bij=1,否则Bij=β>1。通过该二阶相似性的目标约束,使得原始网络拓扑空间中具有相似全局链接结构关系的节点的低维表示也尽可能相似。
为保持原始网络空间节点的局部结构,节点低维表示映射过程中,要使存在直接链接的节点对的低维表示尽可能相似,因此对这类节点对进行约束,如果其低维表示的距离较远则引入较大的惩罚。构建一阶相似性损失函数L1st,定义dii=,则优化目标:
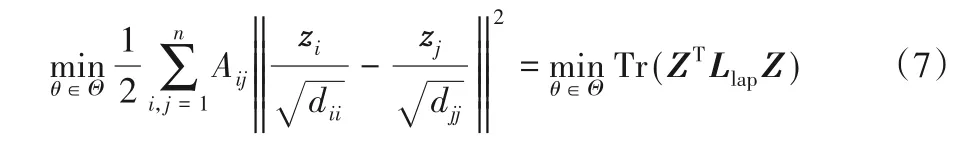
为了使网络节点映射为低维特征空间表示的过程中,同时保持网络局部及全局拓扑结构,将一阶相似性与二阶相似性综合得到目标函数:

1.4 保持网络潜在聚类结构
在低维表示空间引入聚类损失,使学到的网络嵌入能够更好地保持网络聚类结构,基于深度聚类算法DEC,将节点聚类融合到节点低维表示模型,利用节点聚类结构对低维表示进行进一步优化。将低维表示的节点向量zi(i=1,2,…,n)进行聚类,设节点zi属于类uj的概率为qij(qij∈Q),表示节点zi属于类中心uj的相似度,学 生t-分 布(Student’s tdistribution)为:

因此,将节点低维表示的类分布Q与目标分布P拟合,采用KL散度衡量,得到目标函数:

1.5 CADNE算法实现
模型的训练主要分成两部分:第一部分是网络拓扑结构保持部分(流程步骤1)~8)),即模型预训练,通过对深度自编码模型的编码器encoder 以及解码器decoder 进行训练,采用Adam 优化目标函数Lae,使得节点低维表示过程中同时保持网络结构的局部以及全局结构特性;第二部分根据节点聚类结构对节点低维表示进行优化(流程步骤9)~13)),对编码器的编码过程进一步训练,使得节点的低维表示过程保持聚类结构。通过两部分的模型预训练以及社区结构的优化训练,得到构建深度网络模型参数及最终节点低维表示Z。本文提出的CADNE模型流程如下:
输入 网络G=(V,E)的邻接矩阵A;
输出 节点低维表示矩阵Z,模型参数θenc、θdec。


2 实验设计与结果分析
为验证提出的基于社区优化的深度网络嵌入方法CADNE 的有效性,与经典的网络表示学习模型进行对比,在数据集20NewsGroup、Cora、Citeseer、BlogCatalog 上进行测评。各数据集的统计信息如表1所示。
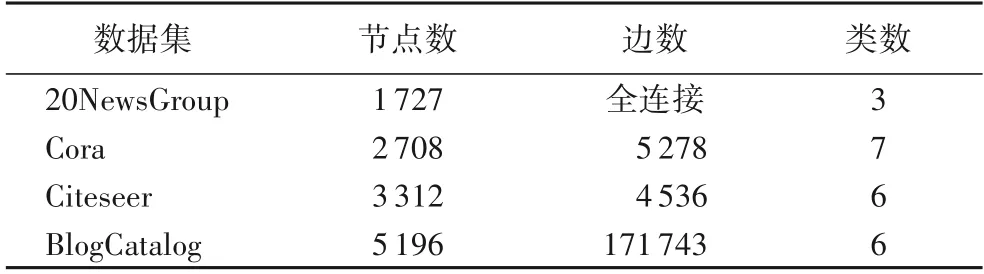
表1 数据集属性Tab.1 Datasets attributes
为了更好地评价本文所提出的模型方法,在实验部分与7个代表方法进行对比分析,包括:
1)DeepWalk:该方法通过在图中进行随机游走得到的节点序列,将序列输入使用Skip-Gram模型得到每个节点的嵌入表示。
2)LINE:该方法通过优化保持一阶相似度和二阶相似度的目标函数来学习每个节点的低维表示向量。
3)SDNE:该方法通过构建深层自编码器保留网络一阶相似度和二阶相似度,学习节点的低维表示。
4)DNGR:构建节点间PPMI 关联矩阵,通过降噪自编码得到节点的低维向量表示。
5)M-NMF:基于矩阵分解学习节点低维嵌入表示,模型训练过程中考虑了节点的社区结构。
6)NECS:保持网络节点高阶近邻,同时考虑网络社区结构的矩阵分解模型,学习节点低维嵌入表示。
7)DEC:深度嵌入聚类算法,将网络邻接矩阵作为模型输入进行训练,没有考虑网络的拓扑结构信息。
参数设定:为保证对比公平,各方法的参数设置为默认值,CADNE 参数设置为:γ=10,β=10,batch-size=128,ρ=0.000 1,在编码阶段搭建三层神经网络结构,各层神经元节点数的设置如表2所示。

表2 神经网络各层神经元节点数Tab.2 Neuron nodes in each layer of neural network
2.1 聚类实验分析
使用CADNE模型得到网络节点的嵌入表示,然后将其运用于节点聚类任务,通过聚类的效果评测网络表示学习的性能。聚类算法采用K-means,评价标准采用标准互信息(Normalized Mutual Information,NMI)以及准确率(Accuracy,ACC)[22],这两个指标值越大,说明模型的聚类效果越好,各算法在数据集上10次实验的平均聚类结果如表3所示。从表中可以看出,CADNE模型在Citeseer和Cora上两个评测指标都取得了最好结果,在BlogCatalog 上明显优于除DEC 外的其他基准方法,在20NewsGroup上ACC也取得最优,ACC提升最高达0.525。M-NMF也考虑了网络社区特性,但基于矩阵分解的浅层模型,无法捕获网络更高阶复杂结构特性。NECS方法可以得到类似的结果,通过引入网络社区结构的约束,得到节点低维表示在BlogCatalog以及Citeseer数据集相对于没有考虑社区结构的SDNE 以及DNGR 方法,性能得到提升,但由于基于矩阵分解的线性模型,难以捕获网络节点间复杂的非线性关系。DEC通过深度嵌入聚类,在BlogCatalog 数据表现较好,但缺乏对网络特殊拓扑结构特性的保持,在其他数据集的性能有待提高。SDNE通过综合考虑网络一阶相似度以及二阶相似度,聚类效果优于采用深度训练模型的DNGR,但CADNE 模型在节点低维表示过程中,除了考虑网络的局部及全局拓扑结构,还考虑节点聚集的社团结构进行优化,表现出更好的聚类结果,验证了基于网络节点社区结构进行深度嵌入表示的有效性。
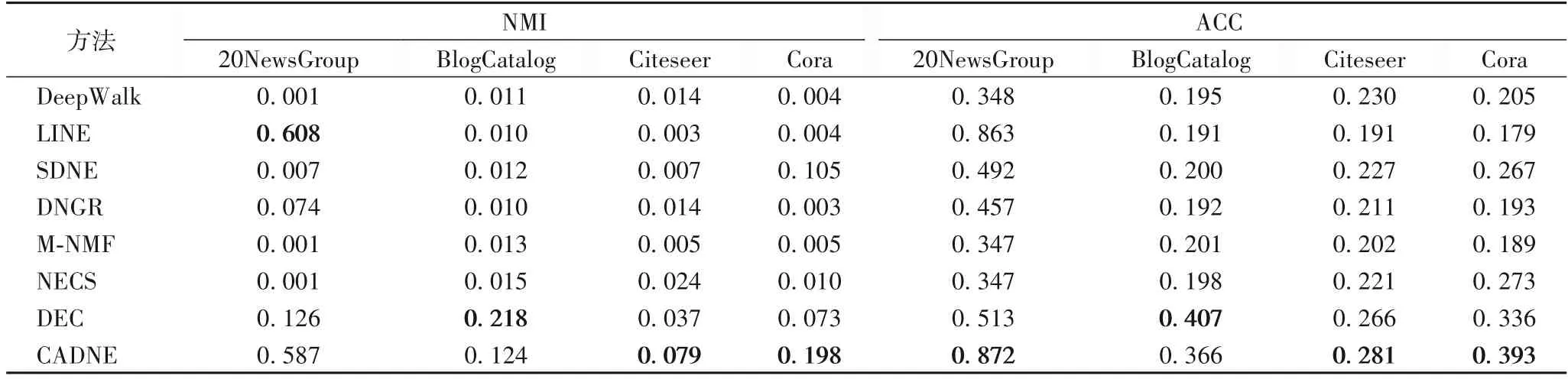
表3 不同网络嵌入方法在数据集上的NMI和ACC比较Tab.3 NMI and ACC of different network embedding methods on datasets
2.2 分类实验分析
CADNE 模型得到节点表示之后,将其运用于节点的分类任务,分类结果的好坏可以有效判断网络表示学习模型学习到的嵌入表示是否包含了网络更多的特性。分类算法采用Liblinear 分类包,和其他网络表示学习方法[19]类似,采用宏平均(Macro-F1)和微平均(Micro-F1)两个指标作为模型性能的评价标准,这两个指标值越大表明模型的分类性能越好。随机抽取10%到90%的节点嵌入表示作为训练样本,其余作为测试样本。在20NewsGroup、Cora、Citeseer、BlogCatalog数据集的多标签分类结果如表4~7所示。

表4 训练样本占比不同时在数据集20NewsGroup上的宏平均与微平均结果对比Tab.4 Comparison of Macro-F1 and Micro-F1 results on 20NewsGroup dataset with different proportions of training samples
由实验结果可知,CADNE 模型分类效果在BlogCatalog、Citeseer、Cora 数据集上两个评测指标都取得最好结果,除Cora 在90%训练比例时微平均略逊于DEC。结果表明,与基线方法相比,该方法学习到的节点低维表示能更好地应用到分类任务。其中,CANDE 模型在BlogCatalog 数据集上优势最为明显,在训练比例20%时比基线方法提升最高达0.512。这在一定程度上表明CADNE 模型结构对网络表示学习有积极的影响。在表6(BlogCatalog)中,当训练百分比从60%下降到10%时,本文方法在基线上的改进幅度更加明显。结果表明,在标记数据有限的情况下,该方法比基线方法有更大的改进。这种优势对于实际应用尤其重要,因为标记的数据通常是稀缺的。在大多数情况下,DeepWalk 性能是网络嵌入方法中最差的,DeepWalk 没有明确的目标函数来捕获网络结构,且所采用的随机游走方式可能引入了噪声。虽然对于全连接网络NewsGroup,CADNE 模型的性能略逊于LINE 方法,主要可能是无法有效通过权重捕获网络中节点间的相似性关系。但在大多数情况下,CADNE 模型的性能是网络嵌入方法中最好的,该方法根据节点聚类结构对节点低维表示进行优化,对编码器的编码过程进一步训练,使得节点的低维表示过程保持聚类结构。因此,该模型学习到的网络表示能更好地推广到分类任务。

表6 训练样本占比不同时在数据集Citeseer上的宏平均与微平均结果对比Tab.6 Comparison of Macro-F1 and Micro-F1 results on Citeseer dataset with different proportions of training samples

表5 训练样本占比不同时在数据集BlogCatalog上的宏平均与微平均结果对比Tab.5 Comparison of Macro-F1 and Micro-F1 results on BlogCatalog dataset with different proportions of training samples
2.3 链接预测实验分析
为了验证CADNE 模型得到的节点低维嵌入在链接预测中的有效性,从低维表示后的样本中随机选取90%作为训练集,采用逻辑回归分类器进行模型训练,使用受试者工作特性曲 线(Receiver Operating Curve,ROC)下面积AUC(Area Under ROC Curve)衡量预测的准确性,较高的AUC 值表示更好的性能。各模型的实验对比结果如表8所示。
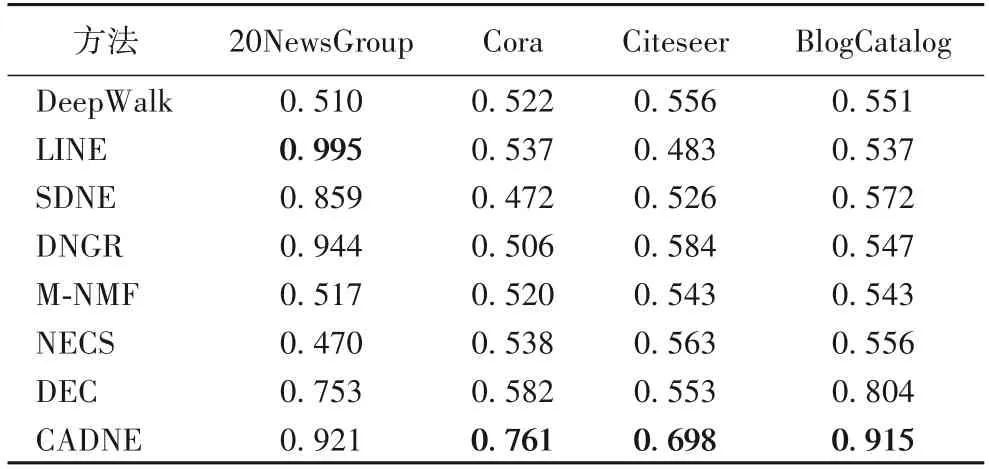
表8 不同网络嵌入方法在数据集上的AUC值Tab.8 AUC values of different network embedding methods on datasets
从实验结果可见,相比已有的网络嵌入方法,本文提出的基于社区优化的深度网络嵌入方法CADNE 在各数据集上准确性都取得较大提升。具体来说,在20NewsGroup 上,LINE和DNGR 性能优于CADNE 方法,主要原因可能是在全链接网络20NewsGroup 上,LINE 通过随机块模型能够获取更加可靠的节点拓扑关系,DNGR 通过构建PPMI 矩阵能够更好捕获节点间的拓扑相似关系,因此取得更好的性能;但在20NewsGroup 上,CADNE 相较于其他基线方法,AUC 提升最多 达0.451。在其他三个数据 集Cora、Citeseer 以 及BlogCatalog 上,本文方法都取得最优结果,比基线方法提高了约0.111~0.378。以上结果表明本文通过结合节点社团结构的深度网络嵌入方法,能够得到更好的节点低维表示。
2.4 可视化实验分析
为进一步评测本文CADNE模型节点嵌入表示的有效性,在20Newsgroup 数据集上与LINE、DNGR 以及SDNE 的可视化结果进行比较。将网络嵌入模型输出得到的节点低维嵌入表示输入t-SNE 得到数据样本在2D 空间的可视化图,其中同颜色的数据点表示同一类别。通过可视化,不同颜色样本点组成的簇间的边界越清晰,说明模型得到的节点表示越好。
从图2(横轴、纵轴是将数据样本点降维到2维空间后,分别在两个坐标的数值)结果可见,LINE 和DNGR 的类边界不清晰,而且类内混淆度比较大,尽管SDNE 能够得到比较好的可视化结果,但不同类的边界也不够清楚;CADNE 则能够得到比较清晰的类边界,三个类间的间距比较大,而且同一个类内相同节点大部分聚集在一起。由此可见,在节点低维表示过程中,引入节点的聚类结构对低维表示进行优化,能够得到类边界更加清晰的节点低维表示。
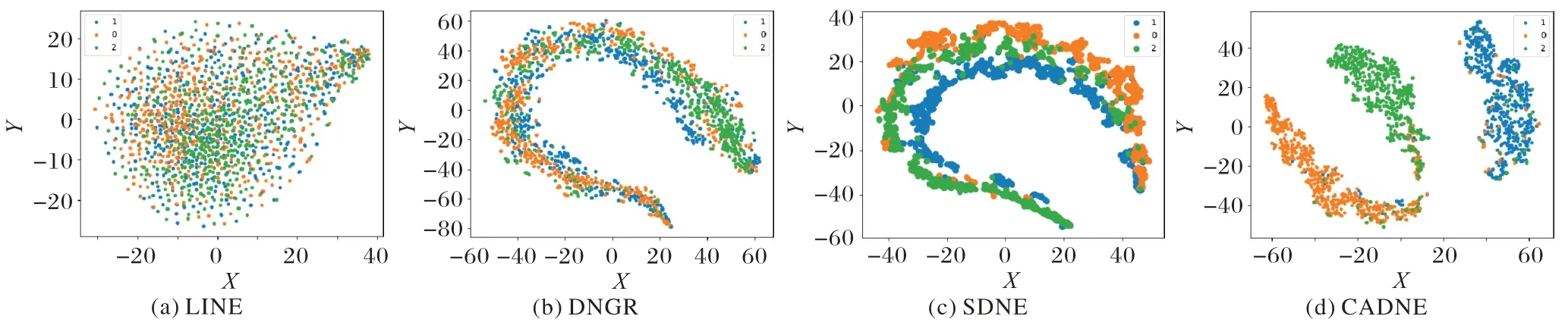
图2 20NewsGroup数据集可视化图Fig.2 Visualization Results of 20NewsGroup dataset
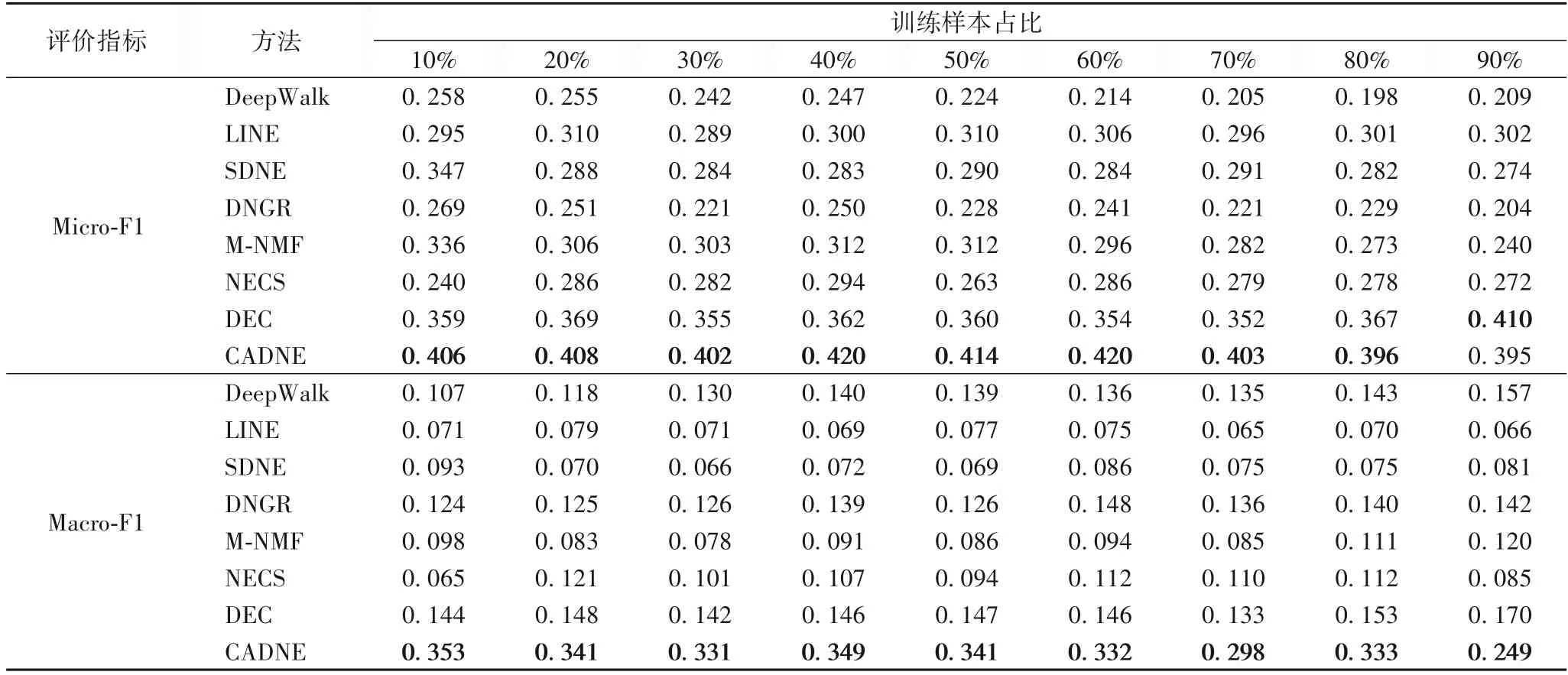
表7 训练样本占比不同时在数据集Cora上的宏平均与微平均结果对比Tab.7 Comparison of Macro-F1 and Micro-F1 results on Cora dataset with different proportions of training samples
2.5 参数敏感性分析
CADNE 有两个超参数:样本重要度参数γ和二阶相似度系数β。这里选择在四个数据集上进行测试,通过实验分析超参数的选择对CADNE 模型在链接预测上的性能。除了当前被测试的参数,其他参数均保持默认值。
图3 显示了γ取值为[0,30]时所有样本数据集AUC 值的分布情况。从结果可见,当γ为0 时,CADNE 取得的效果最差。此时相当于CADNE 模型仅利用了网络拓扑结构中的一阶近邻信息,无法完全保留网络中高阶的相似度;随着γ增大,CADNE 模型的效果先迅速提升,在γ=10 时达到最好之后缓慢下降,在Cora 和Citeseer 数据集上结果比较稳定。因此,本实验设置中该参数设置为10。
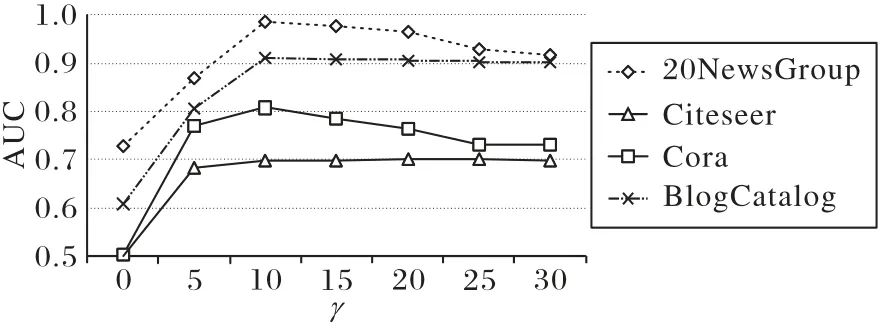
图3 不同参数γ的AUC值Fig.3 AUC values of different γ
图4 中可以得到类似的结果,当β从1 增至30 过程中,开始CADNE 性能迅速提升,到10 取得最优结果,之后缓慢下降。具体地,在β=1 时效果最差,此时将邻接矩阵中零元素与非零元素同等对待进行模型训练,因此会重建更多的零元素,引入的噪声信息影响了最终节点嵌入表示的性能。随着β增加,模型会倾向于重建更多的非零元素,因此效果有显著提升;但过大的β使得忽略零元素的重建过程,性能会降低,因此在实验过程中β设置为10。

图4 不同参数β的AUC值Fig.4 AUC values of different β
3 结语
本文提出了一种基于社区结构优化的网络嵌入方法,在节点低维表示过程中,不仅保持网络的局部和全局拓扑结构特性,而且融合节点潜在的社区特性对低维表示进行优化。打破了传统网络表示学习方法局限,得到更具有表示能力的低维、稠密特征表示。本文提出的基于社区结构优化进行节点低维特征表示的深度自编码聚类模型CADNE,能够同时学习节点的低维表示和节点所属社区的指示向量,在多个数据集上与已有经典网络嵌入方法对比实验表明:CADNE 模型具有较好的节点低维表示能力。
