面向分布式漂移数据流的集成分类模型
2021-07-30尹春勇张帼杰
尹春勇,张帼杰
(南京信息工程大学计算机与软件学院,南京 210044)
0 引言
移动互联网、传感器网络以及人工智能技术的快速发展产生了海量的数据,称之为“大数据”,这些数据具有4V 属性[1]:规模大(Volume),聚集速度快(Velocity),类型多(Variety),价值大(Value)。目前,大数据知识挖掘问题已经受到国内外学者和研究机构的广泛关注,并且大数据挖掘技术已经得到广泛运用。2013年,Wu等[2]探讨了大数据分析的核心问题,并设计了一个大数据挖掘的核心模型;2017 年,Moreno[3]等将大数据分析技术应用于智慧城市,提出了一种适用于不同智慧城市应用场景的基于物联网的通用体系结构;2019 年,Edstrom 等[4]在移动设备硬件设计过程中引入大数据挖掘技术,提出了一种低成本的自恢复视频存储系统,有效地解决了视频数据量大、计算量大带来的能耗问题。
在大型的电子商务网站交易系统、银行业务系统、网络监控、传感器网络等应用场景中,大数据都呈现出了分布式和流动性的特征[5-6],因此,本文的研究重点是具有分布式和流动性技术特征的大数据的分类方法。流式数据也称为数据流[7],可以看作一个有序的数据序列,具有实时、快速、连续、无限等特点,在网络监控系统中尤为常见,表现为网络流量随时间增长,并且隐藏在数据中的知识在动态变化。分布式数据流是指各个节点数据独立但是逻辑上关联的数据流[8],也就是说,虽然数据分布在不同地理位置的局部节点上,但是这些数据有相同的属性集,将局部数据汇总到中心节点,可以学习到性能更好的全局分类器。
分布式数据流挖掘系统既要有局部节点的分析,又要有全局性的模式发现。局部节点的分析处理侧重实时性和高效性,全局分类模式旨在构造全局共享的分类器。整个分布式数据流分类系统由三个部分组成:局部节点数据收集、数据传输和全局分类器的构建。最经典的层次式分布式数据流挖掘框架DS-means模型[9]将挖掘任务分成三个步骤:局部聚类、模式传输和全局聚类,该模型在聚类操作中采用的是经典的无监督K-means算法,中心节点的k值设定根据局部聚类结果动态变化。
由于分布式数据流挖掘系统涉及数据的传输,就必须要考虑到通信的代价,因此,如何在不影响全局分类器精度的情况下降低通信代价是系统设计的关键科学问题[10]。目前使用较多的策略是局部节点只向中心节点传输关键的统计数据而非原始数据,最经典的算法是2008 年Masud 等[11]提出的微簇算法,该算法将局部节点的原始数据先进行K-means 聚类,然后提取簇的统计信息,如方差、均值、样本数目等,但是这个是针对单数据流的。后来Wang 等[12]设计了一个面向分布式数据流的挖掘框架,提出的数据概要思想也是向中心节点传输统计值,这类思想能够有效地降低数据传输代价,避免带宽有限带来的通信限制。
除此之外,数据在经历局部挖掘和传输后质量会有所下降,因此,构造的全局共享分类器需要具备一定的抗噪性能。集成学习技术相对成熟,具有很好的鲁棒性和预测能力,2017年,毛国君等[13]在微簇思想的基础上,提出了BDS-ensemble模型,该模型在构建全局分类器时就是采用了集成学习的方法,该方法可以归纳为学习样本的淘汰策略,即被正确预测的学习样本将会被淘汰,不再用于其他弱分类器的训练,这种策略能够提高对样本的覆盖度。
此外,集成学习还可以处理数据流中出现的概念漂移[14]现象。概念漂移是数据流中一个常见的现象,会很大程度地影响数据流分类算法的性能,它的表现形式是数据流中的实例属性和类别标签的映射随着时间变化,导致预先训练的分类器无法适应新的实例。目前,解决概念漂移主要有三种方法:窗口技术、漂移检测和集成方法。窗口技术最经典的是概念自适应快速决策树(Concept-adaptive Very Fast Decision Tree,CVFDT)算法[15],该算法虽然能适应数据流中的动态变化,但是,窗口大小难以确定,设定太大会影响对概念漂移的检测实时性,设定太小则会增加计算量,影响整个分类器的性能。漂移检测器是一种能够及时检测出数据流分布变化的方法,检测原理通常是基于分类器的表现或者新到来数据本身的信息。漂移检测方法(Drift Detection Method,DDM)[16]是经典的基于统计过程控制的检测器,该方法认为在分类器训练方法收敛的情况下,分类器的错误率会随着训练样本数目的增加而减小,否则,证明数据流中存在概念漂移。ADWIN[17]通过比较两个时间窗口的平均值来检测数据分布的变化,当两个时间窗口的平均值变化较大时,则说明发生了概念漂移。集成学习方法是将多个弱分类器通过加权等方式组合成集成分类器,集成学习的框架如图1所示。
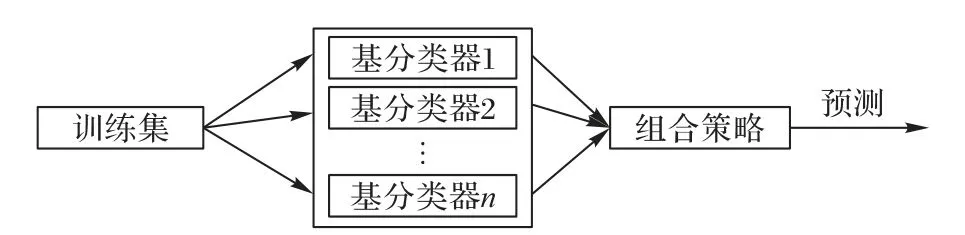
图1 集成学习框架Fig.1 Ensemble learning framework
在集成学习中,基分类器的训练数据一般是由原始数据集bootstrap(有放回)抽样所得,或者是将原始数据集划分成n个子集,用子集训练不同的基分类器,这样可以保持基分类器的多样性。基分类器的组合策略有多种,最主流的是选择多数分类器给出的预测结果作为整个集成分类器的分类结果。现有的研究表明,集成学习比单一的分类器预测准确率更高,并且具有很好的鲁棒性。在数据流分类算法中,集成方法可以分为两种:基于块和在线学习方法。基于块的方法是将到达的实例分为固定大小的数据块,对每个数据块进行分类器的训练,这种方法对时间和内存的要求比较高;在线学习方法是对到来的训练实例进行增量学习,学习出一个从一组属性值到一个类标的映射函数[18],可以满足时效和内存的限制,但是在分类准确率上稍逊于基于块的方法。基于块的方法中最经典的是数据流集成算法(Stream Ensemble Algorithm,SEA)[19],该算法一直从新的数据块中学习新的分类器,并将分类器加入到集成模型中,当基分类器的数量达到上限,新创建的分类器就会替代过时分类器(分类性能比新分类器差),由于基分类器是根据不同的数据块创建的,因此该算法能够保持基分类器的多样性,避免过拟合的情况发生。在线学习方法最经典的是动态加权多数投票(Dynamic Weighted Majority,DWM)算法[20],该算法中的基分类器的权重是动态更新的,当基分类预测错误,它的权重会相应减小。当集成模型对训练实例错误分类,则会创建新的分类器重新学习新的概念,权重太小的分类器会被淘汰,每次删除和添加分类器,权重会进行归一化操作,避免新的分类器权重过大,对整个集成分类结果起主导作用。在线学习的思想在漂移检测中也经常用到,如文献[21]提出的基于在线性能测试的漂移检测方法,该方法在每个子训练集上进行在线学习,检测出真实漂移位点,可以区分真实漂移和由噪声导致的伪概念漂移。
文献[22]中提出了在线主动学习集成模型(Online Active Learning Ensemble model,OALEnsemble),是近两年解决概念漂移最具代表性的模型,该集成分类模型由一个稳定分类器和一定数目的动态分类器组成,采用多层阻尼滑动窗口存放数据来构建分类器,通过权重的动态变化来适应概念漂移。稳定分类器的作用是跟踪数据流分布的长期趋势,以适应概念渐变漂移;动态分类器可以迅速捕捉突变漂移,及时更新集成分类器。由于该模型采用多层窗口技术,因此,每个分类器从创建时刻起,需要学习后面到来的所有实例,因此需要一定的空间来存储数据块,而且重复的计算会使得处理数据流时间复杂度较高,不适用于分布式挖掘环境中。本文在OALEnsemble 基础上改进,同样构建两种分类器:动态分类器和稳定分类器,动态分类器通过基于块的方法创建,稳定分类器通过在线学习的方法更新。稳定分类器在部署到数据流环境之前已经创建完毕,在分类过程中选择最具价值的实例来更新或淘汰稳定分类器;动态分类器通过固定大小的数据块创建,减少不必要的空间开销,因此不管从时间还是空间复杂度上都是优于OALEnsemble,更适用于分布式挖掘框架中。
本文针对现阶段对于大数据的挖掘技术需求,聚焦大数据中分布式和流动性这两个技术特征,提出一个系统的分布式数据流挖掘模型,并在模型的关键挖掘步骤设计相应的算法,最后通过实验证明本文算法的有效性。本文工作主要有两点:
1)BDS-ensemble[13]在局部节点收集数据,并将它们的统计信息发送到中心节点,然后由中心节点根据统计信息重构出样本集来训练集成分类器。该方法虽然能够在较小的通信代价下完成分布式数据流挖掘工作,但是,当数据流中发生概念漂移时,整个分类性能会急剧下降,因为中心节点的集成分类算法不具备漂移自适应性。本文在集成算法上进行改进,使其在漂移数据流环境中也能维持很好的分类性能。
2)OALEnsemble 模型能够很好地处理数据流中的概念漂移,但是该模型的空间复杂度和空间复杂度都较高,本文在不降低分类性能的前提下简化了该模型,使其能运用到分布式数据流挖掘环境中。
1 相关工作
1.1 分布式数据流
假设有n个节点,维度为d,每个节点产生一个单数据流Si(i=1,2,…,n),中心节点接收的数据流S=,每个Si是d维数据元组序列,该定义的数据形态可以在网络流量监控、交易系统等场景下作为收集模型使用,在现实生活中,数据不是一成不变的,数据中隐藏的知识会随着时间变化,因此需要实时更新分类器,以确保分类器的准确预测。
1.2 微簇
当局部节点收集到数据后,需要进行局部模式的挖掘,挖掘的目的是找到一个合适的表达数据块的方式,因为在现实生活中,可能受到带宽的限制,局部节点向中心节点传输的信息不能太多,否则延迟太高,影响分类的效率,然而,如果传递的信息不够全面,就会影响全局分类器的精度。因此,局部模式的挖掘实际上就是一个传输代价和分类精度的平衡优化问题,需要找到一个“紧凑”的表达方式。“紧凑”是指信息容量小,但是具有代表性,并且到达节点后可以恢复,因为全局分类器需要学习恢复的数据集。本文借鉴了微簇模式,先将数据块中的样本通过K-means方法聚类成k个簇,然后将每个簇的簇内样本数、样本均值、平方和、方差和簇的类标识组成一个五元组来代表这个簇。
假设X={x1,x2,…,xm}是一个含有m个样本的簇,其中每个样本都是一个d维的向量xi=,则这个簇可以简化成一个五元组的微簇模式MC=(m,ave,s,var,y),分别代表簇内样本数、样本均值、平方和、方差和类标识,其中类标识是指每个簇样本标签的众数,样本均值、平方和及方差的计算方式如式(1)~(3)所示:

上面定义的微簇模式满足局部模式对于数据集表达方式“紧凑”性的需求,能够使用最小的通信代价传输局部节点收集的数据,当数据到达中心节点时,全局模式需要对各个数据流的潜在的知识模式进行共性归纳,集成学习能够构造一个预测能力较强、概念漂移自适应的分类器,因此,本文将改进现有的集成学习技术,在中心节点创建一个全局共享的分类器。
1.3 概念漂移
数据流中的“概念”,最早将其定义为一组对象的集合,显然这个定义不适用于动态变化的数据流环境,文献[23]中将“概念”定义为底层的数据分布,将“目标概念”定义为待学习的概念或者函数,具体用联合概率分布P(x,y)来表示[24],其中x是d维的特征向量,y是标签。用Pt(x,y)表示t时刻输入特征和目标变量y之间的联合概率分布,在t时刻,每个实例都是由联合概率分布为Pt(x,y)的数据流源生成,当且仅当数据流中的实例都是由同一联合概率分布的数据源生成时,数据流中的“概念”才是稳定的,如果存在x,使得Pt(x,y) ≠Pt+1(x,y),则说明在t时刻发生概念漂移。根据贝叶斯理论,可以将联合概率分布表示为P(x,y)=P(x)P(y|x),因此可以从概率论的角度将概念漂移分为两类:真实漂移和虚拟漂移。先验概率P(x)发生变化,而条件概率P(y|x)不变,因此不会影响决策边界,这种漂移被称为“虚拟漂移”;条件概率分布发生变化,不管先验概率有没有变化,都会影响决策边界,进而影响分类器的学习准确率,这种漂移称为“真实漂移”。文献[25]中根据变化形式,将概念漂移分为四种类型。
突变漂移 突变漂移的表现形式是数据流中的数据分布在很短时间内被另一种分布所取代,这种变化可能会导致分类模型失效。因此,在处理时,要求分类模型有较高的灵敏度,能够及时捕捉数据分布的变化并更新模型以适应后来的数据流实例。
渐变漂移 渐变漂移是一种变化幅度较小的漂移,需要很长时间才能发现,这种漂移对分类模型准确率的影响较小,因为即使发生了,变化前后的概念也是极其相似的。
增量漂移 增量漂移与渐变漂移相似,概念的变化幅度都较小,表现为概念增量式变化,由多个数据分布产生数据,但是数据分布之间相差不大,因此,概念变化也不大。
重现式漂移 重现式概念漂移表现为之前学习的概念经过一段时间后再次出现,在现实生活中很常见,比如,人们关注的主题,如“春运”会在每个年关周期出现。在处理这种类型的概念漂移时,需要把之前学习的知识重复利用,不仅能提高模型的学习准确率,还能避免历史学习资源的浪费。
2 分布式数据流分类框架
分布式数据流的分类模型可以定义为Model=(T,D,O,P),其中:T={t1,t2,…}是局部节点收集收据的时刻序列;D是来自n个局部节点的数据流,为全局分类器提供样本来源;O是对数据流实例的操作算子;P是最终训练完成的全局分类器。
整个挖掘模式如图2 所示,假设网络中有三个局部节点,则整个挖掘框架由三个部分组成:
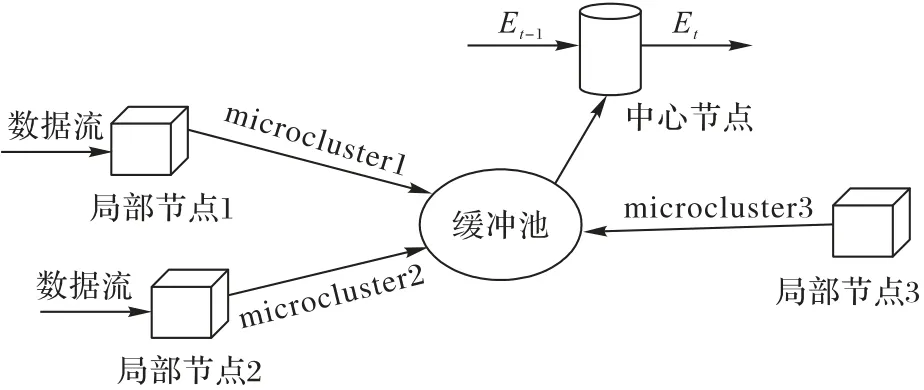
图2 分布式数据流挖掘框架Fig.2 Distributed data stream mining framework
1)局部模式。按照之前设定的时间点序列收集局部节点窗口数据,形成数据块{D1,D2,…},挖掘每个数据块的微簇集{c1,c2,…,ck},ci是指第i个簇的微簇形式,微簇模式是用第一个数据块的微簇集初始化的。假设Dt是当前时刻窗口中的数据,则可以用Dt中的数据对上一个挖掘点所维护的微簇模式MCt-1进行更新,即MCt={MCt-1;Dt}。大数据背景下,更新操作后会增加局部节点维护的微簇的数目,为了防止微簇数目的无限膨胀导致后面中心节点计算量大、学习效率低等问题,局部节点采用几何轮廓相似度函数[26]计算簇之间的相似度,将相似度较高的两个簇合并。
2)模式传输。当微簇模式更新完成后,将其传输到中心节点。
3)全局模式。中心节点设置了缓冲池,等待所有局部节点的微簇模式传输完成后将其发送到中心节点;然后,中心节点采用样本重构算法,将微簇转化成和原始样本具有相同分布特征的合成样本,使用合成样本学习分类器。基于集成学习技术创建的分类器,当一个历史窗口的所有节点的微簇模式都发送到缓冲池后,可以触发全局分类器更新机制,即使用新的实例对全局分类器进行增量式更新。
3 各步骤挖掘算子
根据上面提到的分布式数据流分类框架,本文主要用到的算法有微簇提取、微簇合并、训练样本恢复和全局集成分类算法。其中,微簇提取算法比较简单,主要公式在相关工作中已经介绍,这里不再赘述。
3.1 微簇合并
一个局部节点维护的微簇模式需要不断更新来适应数据的变化,具体方法是挖掘新到来的数据块的微簇集合来增量式更新上一个挖掘时刻维护的微簇模式。这种更新方式会导致微簇的数量无限增加,增加后面样本重构和分类器学习的时间,因此,必须要对微簇的数目加以控制,比如设置阈值,当更新操作中微簇的数目超过给定的阈值,就需要进行微簇合并操作,找到当前维护的微簇模式中相似度最高的两个簇,并将它们合并成一个簇。考虑到微簇模式只是保存的原来簇的统计值,而非数据点,本文用微簇中的均值代表这个簇,因此簇与簇之间的相似度计算可以转化为均值样本的相似度计算。本文根据几何轮廓相似度函数计算两个簇的相似度,然后设定阈值ξ,大于阈值ξ的两个簇进行合并操作。
几何轮廓相似度函数是建立在伽罗华群-单纯型理论[27]上的多维对象亲疏性度量方法,假设当前数据流是S,S是d维数据元组序列,S={x1,x2,…,xn},xi是数据流S的第i个样本,xi=是xi的第j个特征变量,则点集Qi=是样本xi的几何轮廓。样本xs和样本xt的几何轮廓相似度函数为:
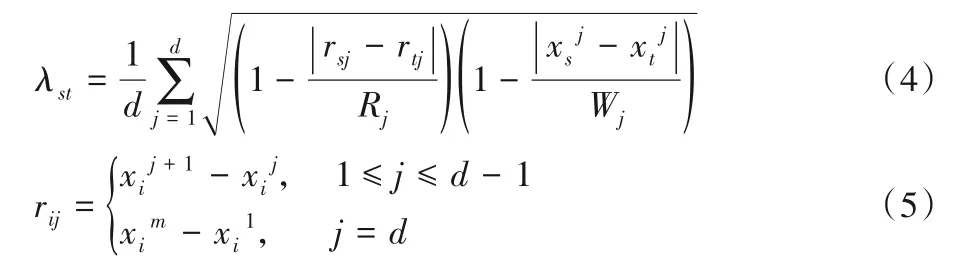

当局部节点维护的微簇数目超过阈值L时,随机选取两个微簇,计算它们微簇均值的相似度λ,然后将λ与设定的阈值ξ比较,如果λ>ξ,说明比较的两个微簇比较相似,需要进行微簇合并操作。用c1和c2表示合并之前的两个簇,用c3表示合并后的簇,因为微簇模式不是直接存放原始数据点,所以,c3的微簇模式不能用之前的方法提取,只能由c1和c2的统计值推导出,如下所示,给出了c3统计值推导过程,其中c1和c2的原始簇的样本集分别为{x1,x2,…xp}和{y1,y2,…,yq}:
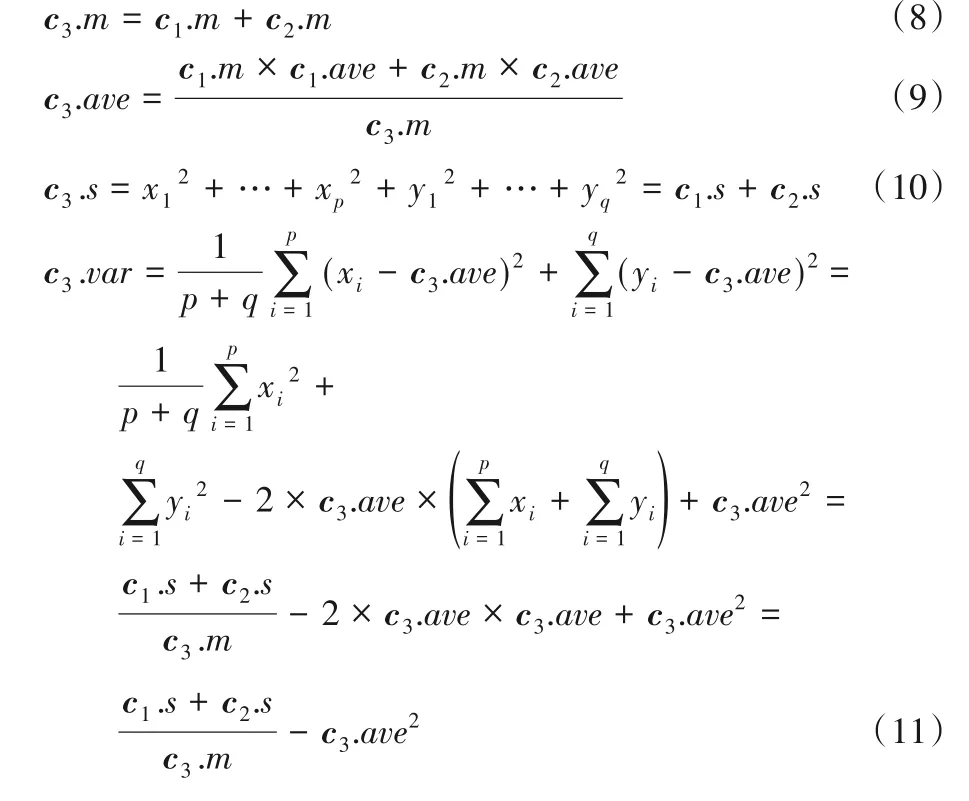
通过式(8)~(11),可以由c1和c2的统计值推导出c3的统计值,这样就能将两个相似的簇合并成一个簇。当增量式更新局部模式时,如果局部模式中的微簇数量超过给定阈值L,就需要选择最相似的簇合并,整个的增量式更新过程如算法1所示。
算法1 Microcluster-merging。
输入 当前数据块挖掘出的微簇集MC*,上一挖掘点维护的微簇模式MCt-1,微簇数量最大值L,簇相似度阈值ξ;
输出 更新后的微簇模式MCt。

算法1 中第2)行用N表示MCt中的微簇数目,从第3)~13)行,如果当前微簇数目一直超过阈值L,就会执行合并操作,即在当前微簇集中随机选取两个微簇c1和c2,用x1和x2分别表示它们的均值向量,如果x1和x2的相似度大于阈值ξ,就会根据式(8)~(11)合并c1和c2,形成一个新的微簇c3,然后在当前微簇集中加入c3,去除原来的相似簇c1和c2,以此方式循环,直到MCt中的微簇数目小于阈值L。
3.2 微簇重构
当所有的局部节点将更新完成后的微簇模式传入到中心节点后,中心节点就会学习一个全局集成分类器,但是微簇集并不是原始的样本,不能作为分类器的训练样本。因此,需要根据微簇的统计信息,重新构造样本集来训练分类器。本文借鉴了文献[13]中提出的样本重构算法,假设原始样本是正态分布的,那么由微簇重新构成训练样本集的过程如算法2所示。
算法2 Samples-remaking。
输入 微簇c,样本数据维度d;
输出 重构训练集X。

在算法2 中,l是重新构成的簇的半径,l的证明过程可以参考文献[13],用簇半径l乘以在-1~1 的随机变量r,可以在簇的均值向量周围生成训练样本集,且生成的样本集和原始样本具有同样的分布。
3.3 全局分类算法
本文改进现有的集成方法,利用重新构成的训练样本集,学习一个高归纳性、抗干扰性强并且可以适应概念漂移的集成分类器,该集成分类器用到了主动学习。主动学习就是从一堆不带标签的样本中按照一定的准则选择一部分来标记,这种学习方式可以在保证分类器性能的同时控制标记成本。
从图3 中可以清楚地看到在线集成学习的框架。三角形和正方形分别表示稳定分类器和动态分类器,具体表示为Cs1,Cs2,…,Csn和Cd1,Cd2,…,Cdn。对于数据流S,将用于动态基分类器的实例I视为每个等大小的数据块M1,M2,…,Mn,而稳定基分类器只需使用实例I进行自我更新。由于标记成本较高,每个数据块只选取最不确定的实例进行标记,并利用标记实例生成新的动态分类器和更新稳定分类器。本文采用混合标记策略[20]来选择每个块中的实例,该策略由不确定性策略和随机策略组成。在不确定性策略中,一个测试实例的裕度值由公式确定:P(yc1|x)-P(yc2|x),其中yc1和yc2分别表示具有最大后验概率和第二大后验概率的类别,预测裕度可以识别出每个块中预测结果最不确定的实例,并以此作为判断实例是否需要标记的依据。具体来说,如果实例的裕度值小于阈值θm,则该实例将被标记。当数据流中出现概念漂移时,裕度值小于阈值的实例数量将显著增加,从而导致标记开销过大。因此,在该策略中,动态地降低阈值θm,以确保对最不确定的实例进行标记,同时最小化标记成本。随机策略可以发现数据块中潜在的概念漂移。它首先生成0 到1 范围内的随机变量φ,然后将φ与阈值σ进行比较。如果φ不大于阈值σ,则实例将被标记。这样,可以对没有被不确定策略标记的实例进行随机标注,捕捉到潜在的概念漂移实例,从而生成更好的动态分类器,有效地更新稳定分类器。

图3 集成模型框架Fig.3 Ensemble model framework
在真实环境的数据流中部署稳定分类器之前,需要对其进行训练。本文使用AdaBoost算法来建立一个稳定的集成分类器。然后,将这个集成分类器部署在数据流中,稳定基分类器在数据流分类过程中进行在线学习。动态基分类器的数目和稳定基分类器一样,都是n,但与稳定基分类器不同,动态基分类器不需要预先训练,而是通过逐渐到达的数据流实例来创建。当方法被部署到数据流中时,数据流被视为等大小的块M1,M2,…,Mn,每个块有m个数据流实例。第一个动态基分类器由块M1创建,表示为Cd1,Cd2由M2创建,其余n-2动态基分类器用相同的方法创建。在数据块中,实例选择标记方法基于上述混合标记策略,具体过程如图4 和算法3所示。
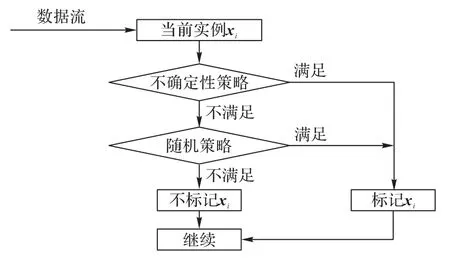
图4 混合标记策略Fig.4 Mixed labeling strategy
算法3 混合标记策略。
输入 测试实例x;裕度阈值θm;随机策略阈值σ;
输出 true 或者false。

当动态分类器的数目达到n个时,新的分类器将取代旧的分类器,具体地说,一旦数据流实例填满数据块Mn+1,新的动态基分类器Cdn+1将由Mn+1构造出来,并加入到集成模型中,此时Cd1将从集成分类器中移除,Cd2取代Cd1的位置,以此类推来响应突发的概念漂移。
集成模型是稳定基分类器和动态基分类器的加权组合,在该集成模型中,稳定的基分类器将始终存在,且权重保持不变。但是动态基分类器会在一段时间内产生并消失,因此动态基分类器的权重会随着时间的推移而衰减。下面的公式显示了每个基本分类器的权重,其中ws和wd分别表示稳定基分类器和动态基分类器的权重。
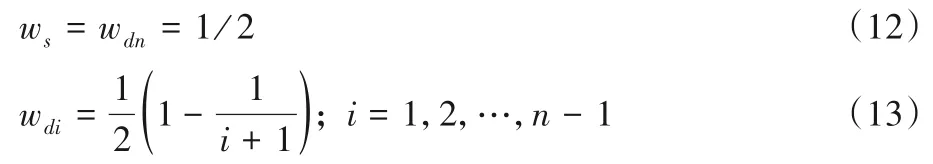
从式(12)和(13)可以看出,ws始终保持不变。动态基分类器越新,其权重值越大,在线集成学习方法如算法4所示。
算法4 在线集成学习。
输入 动态基分类器Cd,稳定基分类器Cs,数据流实例xi,当前数据块M,训练数据集D,数据流S,动态分类器数量n;
输出 集成模型E。

算法4 中设置了一个缓冲区A用来存放被选中标记的实例,对于数据块中的每一个实例,使用混合标记策略确定其是否需要人工标记(第6)行),标记后的实例可以对稳定分类器进行更新(第9)行),然后加入缓冲区A中,最后使用A中的有标签实例创建一个动态分类器(第13)行)。
该集成模型可以有效地缓解数据流分类不准确的问题,但当概念突然漂移时,稳定的基分类器可能无法适应环境,从而影响分类结果。因此,本文将在稳定基分类器中引入abandonment方法[28]。
abandonment 方法的作用是删除集成模型中过时的稳定基分类器,本文给出了分类器中的误差阈值θ,它代表了整个集成分类器所能容忍的单个分类器的最大错误数。也就是说,如果一个稳定分类器的错误预测数达到θ,它将放弃参与投票。因此,对于每个实例I,集成模型将选择满足阈值限制的分类器进行决策,以减少过时概念对分类结果的影响,具体见算法5。
算法5 稳定基分类器的abandonment方法。
输入 数据流实例I,稳定基分类器Cs,最大错误次数θ;
输出 集成模型E。


上面算法中,第2)行初始化所有稳定分类器的错误次数为0,第7)~11)行,如果单个稳定分类器的预测结果和集成分类器不一致,就会被判定会预测错误,增加一次错误次数,当错误次数达到上限θ,集成分类器就会抛弃这个弱分类器。
3.4 算法复杂度分析
1)时间复杂度:假设训练一个实例的时间是Ti,训练稳定分类器的实例数目是Ns,标记一个实例的时间是TL,每用一个实例更新一个稳定分类器的时间是TU,一个数据块中被标记的实例比率是α,数据块的大小是Nd,那么处理一个数据块的时间是Ns*Ti+Nd*α*TL*Ti+Nd*α*TL*n*TU。如果数据流中的实例总数目是N,那么本文提出全局集成分类算法的时间复杂度是O[N/Nd*(Ns*Ti+Nd*α*TL*Ti+Nd*α*TL*n*TU)],约等于O(N)。
2)空间复杂度:假设每个数据块的大小是Nd,窗口中的数据块数量是n,存储每个实例所需空间是Si,那么集成算法所需的空间是O(n*Nd*Si)。
4 实验结果和分析
本文在真实数据集和虚拟数据集上验证本文提出的EDD模型(Ensemble model for Distributed Drift data streams)的有效性,硬件平台为一台酷睿i7,内存16 GB 的PC,使用VM Workstation 在一台主机上构建4 台虚拟机,其中三个虚拟机作为局部节点,一个作为中心节点,以此来模拟分布式环境,在每个局部节点使用大规模在线分析平台(Massive Online Analysis,MOA)[29]来模拟数据流的产生并实施算法。
4.1 数据集与评价指标
本实验主要在4 个数据集上进行:SEA、Radial Basis Function(RBF)、NSL-KDD 和MNIST。其中SEA 和RBF 都是由MOA 数据流产生器生成的,NSL-KDD 和MNIST 是真实数据集。
SEA 数据集一种突变型概念漂移数据流集,有三个属性两个类别,但是决定分类结果的只有两个属性。该数据集会有两次突变漂移,在第3×105和第7×105个实例处。
RBF 数据集是一种渐变式概念漂移数据流集,该数据集生成器预先生成一定数量的中心点,每个中心点由位置、标签和权值确定。然后随机选取一个中心生成样本,权值越高的中心点被选中的概率越高,通过对中心位置的改变来产生概念漂移,本实验使用RBF 生成器生成的数据集有20 个类,在第1.5×105、5×105和7.5×105个实例处发生渐变式漂移。
NSL-KDD 是对KDDCup99 数据集的改进,KDDCup99 是美国空军模拟网的流量监控数据,由MIT林肯实验室收集,被哥伦比亚大学等整理的公共数据集。该数据集是网络连接记录的时间序列,被当成数据流挖掘和入侵检测的标尺数据集,有5×106个以上的训练实例、41 个属性和2 个类别:正常和攻击。NSL-KDD 是KDDCup99 数据集的重采样版本,解决了训练集中类别不均衡问题,同时NSL-KDD 去除了训练集和测试集中的冗余记录,控制训练集和测试集的实例数量,实施实验时不需要随机选取一部分,降低了实验成本,训练集和测试集的数量分别是125 973和22 544,属性数量不变。
MNIST 是一个手写数据集,有6×104个训练样本和1×104个测试样本,每个样本是一个28*28 像素的手写数字0~9 的图像。
本文提出的分布式数据流分类模型需要在多个节点上经过多步骤完成,挖掘的最终目标是要学习一个全局共享的分类器,因此,全局分类器的精度是评价该模型的最重要的指标;除此之外,整个模型挖掘过程中的内存消耗也将作为辅助评价指标。本文的对比模型是DS-means[9]、BDS-ensemble[13]和OALEnsemble[22]:DS-means 和BDS-ensemble 和本文模型一样,都是由局部节点和中心节点组成的层次式挖掘框架;OALEnsemble 是目前性能较好的概念漂移数据流集成分类模型,可以与本文的集成分类模型比较。
4.2 参数选择
本文提出的EDD 模型有三个重要的参数:局部模式中的微簇数量阈值L、基分类器的数量n以及每个数据块M的样本数m。为了确定每个参数的最佳选值,本文在四个数据集上分别实验,对比不同参数下的分类准确率,找到每个数据集的最佳参数,每次实验的准确率都是10 次运算结果的平均值,不同参数下的准确率如表1~3所示。
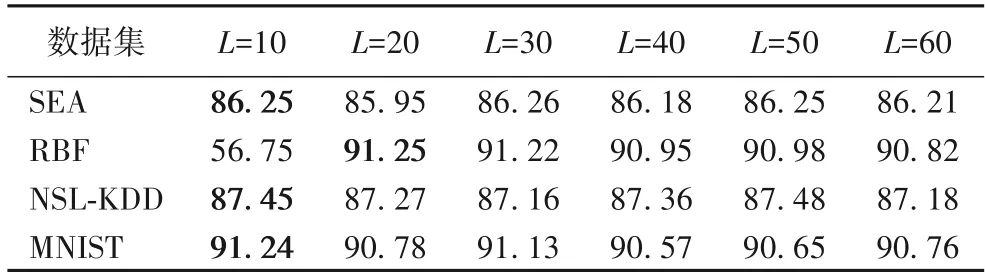
表1 不同参数L下的准确率比 单位:%Tab.1 Comparison of accuracy under different L unit:%
由表1 可知,四个数据集的最佳L参数设定应是10、20、10 和10,当L超过最佳值时,准确率变化不明显,为了减少全局分类器的学习时间,L的参数不能设置过大。在数据集RBF 的实验中,当L=10 时,分类准确率较低,主要原因是RBF中有20 个类别,将微簇最大数目设置为10 时,会导致算法将不属于同个类别的微簇合并,从而导致分类错误。由表2 和表3 得到参数n和m的最佳值分别是20 和35,本文按照参数的最佳选值来设置。
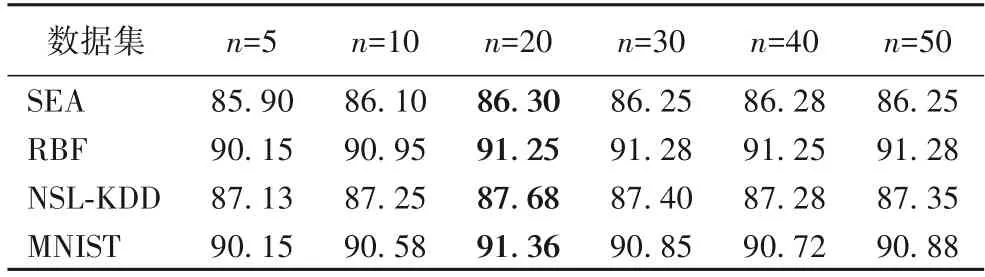
表2 不同参数n下的准确率比 单位:%Tab.2 Comparison of accuracy under different n unit:%

表3 不同参数m下的准确率比 单位:%Tab.3 Comparison of accuracy under different m unit:%
4.3 对比实验
本文从实时准确率、整个过程平均准确率和内存消耗角度分别比较EDD、DS-means、BDS-ensemble 和OALEnsemble,其中,对于SEA 和RBF 数据集而言,实时准确率是指测试点前后10 000 个实例的平均准确率,NSL-KDD 和MNIST 是前后1 000 个实例的平均准确率(因为这两个数据集测试实例较少)。例如,在SEA 数据集上,第2×105个实例的实时准确率是第1.9×105个实例到第2.1× 105个实例的平均预测准确率。图5 给出了各种模型随着数据流实例增多时实时准确率的变化情况。
如图5(a)所示,EDD 模型与其他三种模型相比,准确率一直占优势,刚开始时,各类模型的准确率相差不大,但是由于DS-means 和BDS-ensemble 不能处理概念漂移数据流,因此,在3× 105和8× 105个实例处,这两个模型都受到突变漂移影响较大,并且准确率不可恢复,而EDD 和OALEnsemble则能够响应突变漂移并及时恢复原来的准确率,且EDD 在整体准确率上略高于OALEnsemble。
如图5(b)所示,在RBF 数据集上,各个模型的分类性能相对稳定,特别是EDD 和OALEnsemble,渐变漂移对这两个模型的影响不大,但是对于无法适应漂移数据流的其他两种模型来说,准确率就会缓慢下降。总体上,EDD 模型性能最好,DS-means 模型的性能最差,主要原因是这个模型主要挖掘算法是无监督K-means 聚类算法,因此在整体分类效果上肯定比较差。
如图5(c)所示,由NSL-KDD 模拟出的数据流中没有漂移现象,所以分类算法的精度不会受到影响,各个模型的预测准确率都是在一个很小的区间波动,其中本文提出的EDD 模型整体的分类性能都维持在一个很高的水平。
如图5(d)所示,在手写数字集MNIST 上实验可以看出,DS-means 和BDSEnsemble 的准确率较低并且波动幅度较大,而EDD 和OALEnsemble 的波动幅度较小,并且本文提出的EDD分类准确率略高于OALEnsemble。
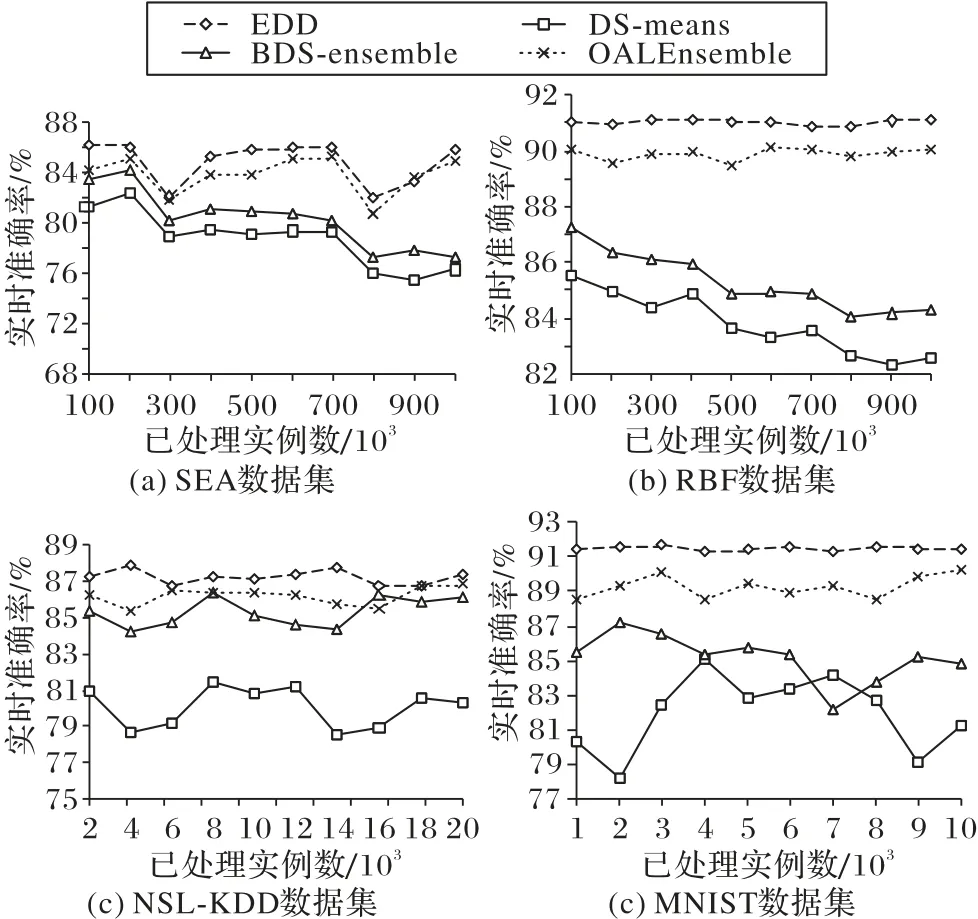
图5 在不同数据集上的实时准确率比较Fig.5 Comparison of real-time accuracy on different datasets
前面几个实验展示了4 个模型在4 个数据集上实时准确率变化情况,每个实验中设置了10 个检测点,考虑到检测点设置可能具有偶然性,下面实验比较了各个模型整个过程中的平均准确率,结果如表4 所示。由表4 可以看出,本文提出的EDD 模型具有较高的整体分类准确率,综上,不管从实时分类性能还是整体准确率,EDD 模型相较于其他三个对比模型,都有显著的提升。除此之外,分布式数据流分类算法还需要考虑代价和精度的平衡问题,前面的实验中已经证明本文模型在精度上的优势,下面实验主要描述了各个模型中心节点的内存消耗随着时间增长的变化情况。

表4 在不同数据集上的平均准确率比 单位:%Tab.4 Comparison of average accuracy on different datasets uint:%
如图6 所示,随着处理实例时间的增长,内存消耗都逐渐增加,DS-means内存消耗较少,主要原因是K-means聚类较为简单,空间复杂度较低,但是在面对概念漂移数据流时,DSmeans 和BDS-ensemble 模型准确率会急剧下降并且无法恢复,而EDD 模型受漂移影响较小,并且从实时准确率角度来看,本文模型明显高于这两个模型。与OALEnsemble 相比,EDD 内存消耗略低,并且在各个数据集上分类性能都优于OALEnsemble。在大数据环境下,面向分布式漂移数据流,本文提出的EDD 模型可以在较小的内存代价下获得较大的分类准确性的提升,并且能够适应数据流中的概念漂移,是平衡代价和精度的较优化的解决方法。

图6 内存消耗随时间变化情况Fig.6 Memory consumption varying with time
5 结语
随着互联网、传感设备的发展,数据量急剧增长,在大数据挖掘理论和方法上的需求越来越迫切,本文从大数据的分布式和流动性特点出发,系统化地设计了大数据的挖掘模型和对应的算法,同时,考虑到数据流中可能存在的概念漂移现象,在挖掘模型的中心节点处,改进现有的集成分类算法,提高模型对漂移的适应能力。本文提出了分布式数据流的挖掘框架,能够平衡分类精度和通信代价。最后,将本文提出的模型与其他分布式数据流挖掘模型和概念漂移分类模型进行对比,结果表明本文的模型具有更好的分类精度和稳定性。
本文提出的模型还有以下缺陷:1)本文借鉴的样本重构算法是假设数据集中样本是正态分布的,如果数据分布不规范,可能会导致集成分类器分类精度的下降;2)本文提出的集成分类模型是基于块的方法来学习弱分类器的,因此在大数据背景下会导致内存消耗过大的问题。
