基于模糊推理的模糊原型网络
2021-07-30吕良福焦一辰
杜 炎,吕良福,焦一辰
(天津大学数学学院,天津 300350)
0 引言
近年来,深度神经网络的发展大大提高了图像分类的准确性与有效性。然而,这种方法需要大量的标记数据进行训练,数据不足会导致过拟合、泛化差等一系列问题。为了解决这个缺陷,只需少量标记数据的小样本学习应运而生[1]。
对于一个新事物,人类只需要从简单的几张图片就可以认识它,小样本学习正是模仿这种能力,使得模型在学习一定量的数据后,只需要少量的样本就可以对新的图像进行正确分类。一个简单的小样本学习方法是使用图像增强的手段[2-3],通过对一张图片进行旋转、放缩等操作来扩充数据集,再利用扩充后的数据集训练模型。元学习的引入加速了小样本学习的研究进度,它将几张图片划分为一个任务,利用一个个任务进行模型训练,能够有效地防止小样本学习因数据过少而产生过拟合。早期小样本学习在图像分类中的研究大都是在模型结构、度量函数的基础上展开的,比较典型的有模型无关的元学习(Model Agnostic Meta Learning,MAML)方法[4]通过调整梯度学习规则来进行模型参数更新,匹配网络(Matching Network,MN)[5]利用余弦相似度度量目标图像与各类图像的相似性进行分类,以及原型网络(Prototypical Network,PN)[6]通过度量目标图像到各个类别原型的欧氏距离来进行分类等方法。后期比较新颖的解决小样本学习方法也是如此,如利用语义信息进行图像分类[7]、图神经网络方法[8],还有一些类似于多模型融合方法[9]等。
这些方法无论从理论上还是数值实验方面,均取得了不错的效果;但它们仍然忽视了数据集具有模糊性的缺陷,这会对实验结果产生一定的影响。本文受深度模糊神经网络[10]的启发,引入模糊神经网络作辅助嵌入来降低数据的模糊性和不确定性。模糊技术可以模拟人类的逻辑推理,执行判断和决策功能,模糊神经网络在模糊的技术上增加学习能力,能够有效降低数据集中模糊和不确定的部分。深度模糊神经网络[10]一文初次将模糊技术引入到深度学习,文中将模糊神经网络和简单的全连接神经网络进行结合,验证了模糊神经网络确实对降低数据的不确定性、模糊性有一定帮助。本文考虑到在小样本分类任务中也存在着数据模糊的情况,但文献[10]中模型忽视了图像的空间结构信息,且不适用于小样本分类,故尝试将其模糊神经网络部分抽离引入到原型网络中,作为辅助特征提取器,通过对数据集中的模糊数据进行逻辑推理来提升小样本分类任务的精度。本文将模糊推理与神经网络进行知识融合得到了新的特征提取器如图1 所示。对于输入图像,模型从模糊部分(方形部分)、神经网络部分(圆形部分)获取图像知识,形成最终的特征向量;再利用得到的特征向量,应用原型网络来对图像进行分类。在这种机制下,本文模型可以利用模糊推理和神经网路各自的优势来获取最佳性能。

图1 带有模糊推理的特征提取器Fig.1 Feature extractor with fuzzy reasoning
本文的主要工作总结如下:1)将模糊神经网络系统应用于小样本学习以获取图像的模糊知识,相比传统CNN 结构,带有模糊推理的模型效果更优;2)本文方法在基于度量的小样本学习方法上取得了很大的性能提升,如原型网络;3)本文模型仅在特征提取阶段做出改进,极易推广,可以推广到其他相关任务中;4)在小样本分类的多个数据集上验证了模型的有效性。
1 相关工作
1.1 小样本学习
小样本学习的提出,成功克服了深度学习依靠大量标签数据的缺陷,元学习的引入也防止小样本学习因数据过少而过拟合。早期的小样本学习主要使用基于模型、基于度量等方法。其中基于模型的方法主要是调整模型的结构来达到快速更新参数的目的。例如,元网络(Meta Networks,MN)[11]跨任务学习元级知识,并通过快速参数化来快速泛化偏差。模型包含两个学习器,分别为基础学习器和元学习器。元学习器用于学习任务之间的泛化信息,并使用记忆机制保存这种信息;基础学习器用于快速适应新的任务,并和元学习器交互产生预测输出。MAML方法通过调整梯度学习规则的方式来改进模型。该方法在支撑集上训练一组初始化参数,更新方式为然后在初始参数的基础上利用查询集进行一步或多步的梯度调整,更新方式为θ=θ-来达到仅用少量数据就能快速适应新任务的目的。该方法模型简单有效,同时能够与任何经过梯度下降训练的模型兼容,并且适用于各种不同的学习问题,包括分类、回归和强化学习,因此不少学者对其进行了扩展,如任务无关的元学习(Task Agnostic Meta Learning,TAML)[12]、元随机梯度下降(Meta-Stochastic Gradient Descent,M-SGD)[13]等方法。
基于度量的方法主要思想是:若一个模型在某一域上具备了度量两张图像相似度的能力,那么给定一张目标域的样本图像,就可以找到与它相似度最高的带标签实例。它采用一种简单的架构来学习深度嵌入空间进行知识传递,目标是学习一个从图像到嵌入空间的映射,在该空间中,同一类图像的类内距离最小,而不同类图像的类间距离最大。基于度量学习的方法主要依赖于学习一个信息相似性度量,这一点已被有代表性的工作证明了[14-15]。其中,匹配网络利用神经网络作特征提取器提取图像特征,并利用余弦相似度来做分类的度量标准。在源域上将少量带有标签的图片和大量无标签的图片同时进行训练,通过无标签目标分类的准确率来辅助特征提取器进行训练。这种类似于元学习的方法,可以很自然地过渡到目标域。同时,为了更好地挖掘训练过程中的完整信息,匹配网络利用双向长短期记忆网络来帮助模型学习注意力机制,从而使得度量学习方法更加鲁棒。PN 借助卷积神经网络提取图像特征,获取图像的特征向量,利用欧氏空间的原型损失函数学习一个度量空间,在这个空间中,可以通过计算到每个类别原型表示的欧氏距离来进行分类。由于这种方法的简单性和良好的性能,许多扩展改进方法被提出。例如,半监督小样本学习[16]方法证明利用未标记样本比纯粹监督的原型网络效果更好;任务自适应度量算法(Task Dependent Adaptive Metric,TDAM)[17]使用度量缩放方法来改变小样本算法的参数更新方式。
随着小样本学习的不断研究与发展,新的方法逐渐被提出,如基于语义和基于图神经网络等。文献[18-19]中指出,结合附加语义信息可以对小样本学习进一步改进。在文献[20-21]中结合图神经网络的相关知识对小样本学习进行优化。此外,还有一些其他研究也为小样本学习的发展做出了重大贡献,如在文献[22]中采用数据增强的方法来处理小样本学习任务等。
1.2 模糊深度学习
考虑到系统的复杂性与所需要的精确性之间的矛盾,且一般复杂系统所具有的不精确性、不确定性,模糊逻辑和神经网络作为两种基本方法,各有优缺点。神经网络具有适应性学习的优势,模糊理论则具有模拟人的逻辑推理的能力,模糊深度学习结合二者各自的优势具有逻辑推理和自适应性学习能力[23-25],以及模糊神经网络本身具有可解释性[26-28]。
模糊集[29]的概念以及隶属函数的提出,为处理具有模糊性和不确定性的信息提供了理论基础。模糊理论在模糊逻辑[30]、模糊推理[31]等相关领域得到了广泛的应用。随后,人们逐渐将模糊逻辑同人工神经网络相结合形成模糊神经网络,改进了模糊逻辑不能自适应学习的缺陷。Bodyanskiy等[23]提出了一种基于广义模糊神经元的自编码器,以及它的快速学习算法。该编码器同人工神经网络类似,采用多维非线性突触相连接,在每个突触内部采用模糊推理。整个系统可以作为深度学习系统的一部分,具有学习速度快、调整参数少的特点。深度层叠神经网络(Deep Cascade Neural Network,DCNN)结构[24]是对模糊神经网络中神经元的一种扩展,前一个输入信号在神经元中运算同时,将结果传递给后一个神经元运算。这种结构较为简单,并且具有处理速度快、近似性好的特性。另外带有辅助支持向量机(Support Vector Machine,SVM)级联的深度模糊规则图像分类器[25]指出当主分类器为单个图像生成两个高度可信的标签时,基于SVM 的辅助器起到了冲突解决器的作用,该方法在手写字识别的问题上具有较高的精度。
传统的深度学习模型结构常被看作一个黑盒子,处理过程不透明,于是有一大批学者尝试利用模糊神经网络的逻辑推理结构来解决神经网络不能够解释的性能。Yeganejou等[26]建议通过将深度神经网络与模糊逻辑相结合来创建更易于理解的深层网络,提出了一种可解释的深度卷积模糊聚类器。该聚类器首先使用卷积神经网络作为特征提取器,然后在得到的特征空间中进行模糊聚类,之后再使用Rocchio的算法对数据点进行分类。Xi等[27]提出了一种带有模糊逻辑规则的卷积神经网络结构,该结构是通过创建一个神经模糊分类器的分类层,并将其集成到深度神经网络结构中来实现的。这里的分类层是利用径向基函数(Radial Basis Function,RBF)神经网络来实现。通过这种结构,可以直接从深度学习结构中提取基于语言模糊逻辑的规则来提高整个系统的可解释性。
此外,现实世界中的数据往往存在一定的模糊性和不确定性,而传统的深度学习模型是完全确定的,不能解决数据的模糊性和不确定性。这一问题给数据的理解和分类任务带来了极大的挑战。Deng 等[10]为降低数据的不确定性,提出了一种将模糊学习的概念引入到深度学习中来克服固定表示法缺陷的模糊系统。该系统的主体是一个深层神经网络,它从模糊和神经表示两方面获取信息,然后,将这两种不同的信息融合在一起,形成最终的分类表示。区间2型直觉模糊LSTM 神经网络[32]一文提出了一种基于长短期记忆机制的区间型直觉模糊神经网络。该网络将长期-短期机制引入模糊神经网络,有效地提高了长期知识的记忆能力。
不同于上述框架,本文模型利用模糊神经网络能够降低数据模糊性和不确定性的特性,将其应用于小样本学习中来对小样本现有学习方法进行改进。其次,考虑到原型网络较为基础,比较简单有效,本文将模糊知识应用于原型网络使得模型从模糊神经网络和原型网络两个方面获取知识,通过知识融合手段得到图像最终特征,从而进行分类。
2 模糊原型网络
2.1 问题设置
小样本学习中,将数据集D={(x1,y1),(x2,y2),…,(xn,yn)}分成两个部分,分别为模型训练数据集Dtrain和模型测试数据Dtest,其小样本学习每次的训练方式为N-way,K-shot,即从训练集Dtrain中随机抽取N个类别,每个类别包含K个样本作为支撑集S,在剩余示例中抽取查询集Q。小样本学习就是在给定的支撑集下,最小化查询集中示例的预测损失。
2.2 原型网络
考虑到小样本学习的基本模型中,原型网络较为简单有效,本文特将模型建立在它之上,通过实验证明模型的有效性。

其中:Si为支撑集S中的第i个类别。通过计算查询集中的样本点到各个类别原型pi欧氏距离的softmax 来预测图片的标签。其查询点的类别分布为:
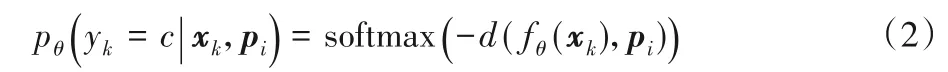
这里的嵌入函数fθ(·)就是本文需要学习的神经网络架构。
2.3 模糊原型网络
现实生活中的数据往往具有一定的模糊性和不确定性,传统的深度神经网络是完全确定的,不能降低数据的不确定性,模糊神经网络具有人脑的逻辑推理能力,本文尝试引入模糊神经网络来解决小样本学习中深度神经网络完全固定的缺陷。
本文所提模型采用基于度量的小样本学习方法,分别通过传统卷积神经网络和模糊神经网络来获得各个图像的特征向量,然后利用这些特征向量计算各个类别的原型表示,通过度量查询集中的样本到各个类别原型的欧氏距离来获取待查询点的分布状态。
不同于其他小样本学习方法,本文在获取图像原型时分为模糊神经网络模块、深度神经网络模块和知识融合模块三个部分。对于模糊神经网络模块,为了获取模糊神经网络的输入特征,先将图片通过函数,该函数是一个浅层神经网络,主要负责将图片映射为特征。映射后的特征被传递到模糊神经网络,该网络有三个网络层,分别是输入层、隶属函数层和模糊规则层,其具体结构如图2。输入层接收特征并将其传递到隶属函数层,它的每个节点被分配给多个带有参数c和σ的隶属函数。这里,输入的是n维特征,用xi来表示输入特征的第i个节点。隶属函数计算的是该节点属于某个模糊集的程度,其中第m个模糊神经元μm(·):R→[0,1]将输入的第i个节点xi的模糊度映射为:

这里选择的是更为广泛的高斯隶属函数,参数c和σ2分别为均值和方差。之后,在模糊规则层执行一系列的“and”模糊逻辑运算,运算输出定义如下:
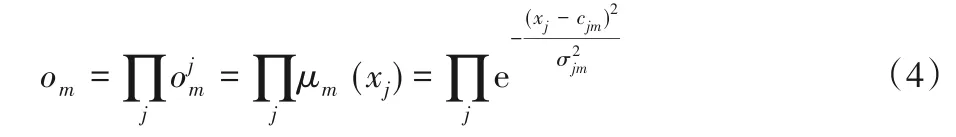
该部分的输出为模糊度。考虑到原型网络的特征原型是一个高维向量,本文用一个映射将模糊部分输出与深度学习部分对齐。对于整个模糊神经网络用嵌入函数来表示(见图2)。

图2 模糊神经网络模块Fig.2 Fuzzy neural network module
本文在引入模糊神经网络的同时也保留了传统原型网络的优势部分,即图像同时输入到深度神经网络部分。在这里,通过带有参数θ1的嵌入函数f将图像映射为特征向量。
在知识融合部分,考虑到拼接组合将导致维度过大,会增大损失,且尝试后并没有较好的效果,本文采用文献[19]中介绍的融合方法,即利用线性组合的方式将模糊神经网络和深度神经网络各自提取的知识进行整合。通过引入可学习的λ,模型可以自适应地学习模糊神经网络和卷积神经网络各自所学习到特征的比重。对于含模糊信息较多的数据集,模糊神经网络将分配到更大的权重。
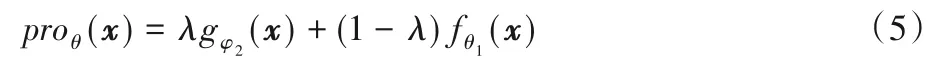
proθ(·)为最终的原型嵌入函数,参数θ={θ1,φ1,φ2}。对于每个原型为其嵌入支持点所属类别的均值向量:

训练过程同传统的原型网络类似,根据查询集中的点到嵌入空间中原型的欧氏距离上的softmax,来生成查询点x在各个类上的分布:
其中:φ={θ1,φ1,φ2,λ}。损失函数部分选取分类任务中常用的负对数似然函数,即:

模型通过Adam 优化器来最小化该损失。其中,对于一个训练批次的损失计算如下:

3 实验与分析
3.1 数据集
本文利用几个广泛使用在小样本学习中的数据集Omniglot[16]、miniImageNet[5]进行实验,并分别同原型网络和目前一些主流的小样本学习方法进行比较来验证模型的有效性。
Omniglot 包含50 个字母,由1 623 个手写字符构成,其中每个字符都有20 个不同的样本。为了同传统的原型网络进行比较,本文采用类似的处理方式,先将灰度图像大小调整为28×28,同样以90°旋转图像来增加字符类。数据集的分割也使用1 200个字符和旋转后的字符类,共4 800个类进行训练,余下的类连同旋转后的字符类用于测试。
miniImageNet 有100 个类,它的每个类中包含有600 张84×84图片,共计60 000张图片。其中64个类作为训练集,16个类作为验证集,20 个类作为测试集。为了更好地同传统的原型网络进行比较,本文在该训练集下同样尝试30-way 1-shot和20-way 5-shot两种训练模式,其对应的查询样本数均为15。
3.2 架构
本文模型主要有三个模块,模糊神经网络部分完全是由式(3)、(4)获取,如图2 所示,先将其输出维度通过一个线性层进行扩充,同深度神经网络对齐。对于深度神经网络部分,选择深层的网络骨干更有利于模型效果的提升,但考虑到实验对比的公正性,仍然采用原型网络中的四个卷积块Conv4作为本文的网络骨干。
模糊神经网络前的浅层卷积网络模块则是完全使用文献[8]中的嵌入架构,该架构由四个卷积层和一个全连接层组成,其具体细节在两个数据集上略有不同,但最终都得到120维的嵌入。这种轻量级架构能够突出模型的简洁性。
3.3 结果
分别在Omniglot、miniImageNet 两个数据集上对本文算法模型同原型网络PN、匹配网络MN[5]、模型无关的元学习MAML、图神经网络(Graph Neural Network,GNN)、边缘标记图神经网络(Edge-Labeling Graph Neural Network,E-LGNN)[33]等目前主流的小样本学习方法进行比较。在Omniglot数据集上设置了5-way和20-way两种实验设置,在miniImageNet上设置了5-way 一种实验设置,实验样本数则是采用小样本实验常用的1-shot和5-shot。由于原型网络在miniImageNet上的实验是采用20-way 5-shot和30-way 1-shot两种实验设置,本文也对这两种设置进行了实验,同原型网络单独对比。在其训练过程中,设置初始学习率为0.001,并且每30个批次衰减到原来的1/10,总计训练300 个批次。考虑到文献[34]统一小样本的查询样本数为16,文中也采用相同的实验设置。在Omniglot 数据集上,本文把原型网络中训练类数为60 改为标准的小样本分类,设置最大批次数为1 000,且训练200个批次后在验证集上性能没有提升则终止训练。训练过程中设置初始学习率为0.001 并且每200 个批次衰减为原来的1/10。另外,在所有实验场景中将模糊神经网络中的参数c按照均值为0.15、方差为0.05 的正态分布初始化,参数σ按照均值为1、方差为0.05的正态分布初始化。
Omniglot 分类:原型网络对Omniglot 分类在训练时每次包含60个类,每个类有5个查询样本,本文对其训练规则进行了简单修改,采用标准的小样本分类,即每次训练包含5 个类和20个类,其中每个类包含16个查询样本。文中收集了近几年小样本学习先进模型在Omniglot 上的结果,并同本文算法模型进行了对比,实验结果见表1。尽管本文模型相比原型网络有一定的进步,但同其他先进模型仍有一些差距。
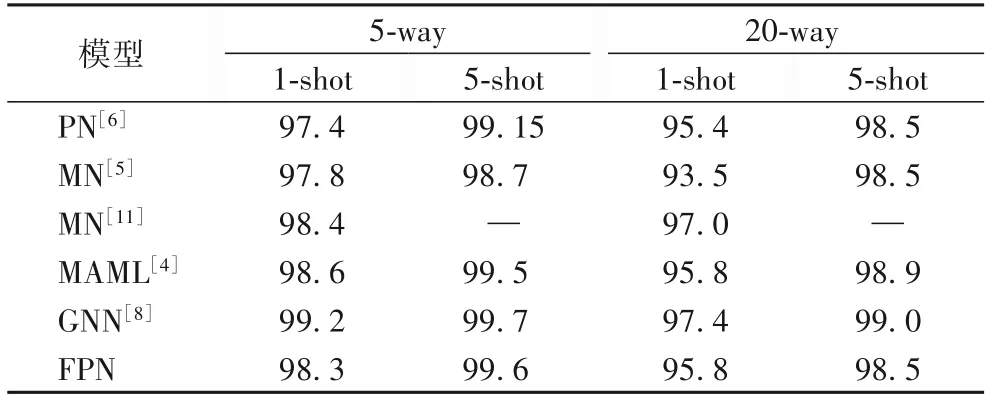
表1 Omniglot上小样本学习分类精度对 单位:%Tab.1 Comparison of classification accuracy of few-shot learning on Omniglot unit:%
miniImageNet 分类:原型网络在每次训练中使用30-way 1-shot和20-way 5-shot两种方式,其对应的测试样本为每类15张。本文同样采用这种实验设置和原型网络进行对比(具体结果见表3),由于实验条件等一些其他原因,这里同原型网络文章中的结果有一定的差异,从表中可以看出模糊原型模型无论是在哪种实验设置下都领先于原型网络。不仅如此,本文还进行了5-way 1-shot 分类和5-way 5-shot 分类的实验设置,将它同目前一些主流的小样本学习方法进行了对比,具体结果见表2。在5-shot 下,相较于这些主流的方法,本文模型效果更好,实验结果比较先进的E-LGNN 仍高出1 个百分点。在1-shot 下,结果虽然略低于E-LGNN,但考虑到主干网络层较浅,同时对原型网络的提高将近5 个百分点,这足以说明本文模型的优秀性能。

表2 miniImageNet上小样本学习分类精度对比 单位:%Tab.2 Comparison of classification accuracy of few-shot learning on miniImageNet unit:%

表3 miniImageNet上FPN与原型网络分类精度比较 单位:%Tab.3 Comparison of classification accuracy between FPN with prototype network on miniImageNet unit:%
为进一步同原型网络进行比较,在miniImageNet 数据集上采用与原型网络相同的实验设置,在学习率为0.01、衰减批次数为20 的条件下训练200 个批次,用训练过程中验证集上的表现来简单地衡量模型的收敛速度和效果。
在图3 中,从损失和精度两个方面来衡量模型在5-way 1-shot 和5-way 5-shot 下的表现,其中:图(a)为5-way 1-shot 设置下损失下降趋势,图(b)为5-way 5-shot 设置下损失下降趋势,图(c)为5-way 1-shot 设置下精度上升趋势,图(d)为5-way 5-shot 设置下精度上升趋势。尽管这种实验条件对FPN 模型有些苛刻,但不难看出,相比传统的原型网络,模糊原型在整体性能上更优。
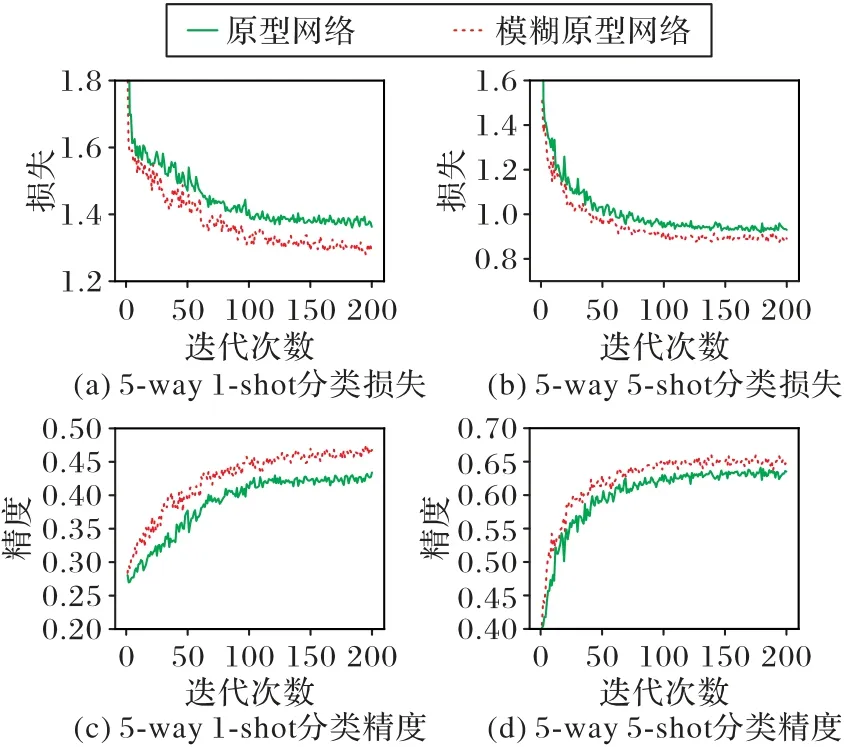
图3 FPN同传统原型网络收敛对比Fig.3 Convergence comparison between FPN and traditional prototype network
此 外,模型的融合方式 为proθ(x)=λ即为模糊神经网络所占比重,本文将λ值初始化为0.5,通过监控λ的值来衡量模糊神经网络对模型的贡献大小。在表4 中,监控了FPN 在5-way 1-shot,5-way 5-shot 以及30-way 1-shot 和20-way 5-shot 下 的λ值,虽然在5-way 和30-way 的条件下λ值有所下降,但仍占有较大的比重,发挥了较大的作用。

表4 FPN中的λ值Tab.4 λ value in FPN
4 结语
本文提出了一种带有模糊推理的原型网络来解决小样本分类问题,这是首次将模糊知识应用于小样本学习。所提模型简单、有效,它不仅能够应用于原型网络,对其他的小样本学习方法也同样适用。数值实验证明,所提出的模糊原型在不同的数据集和设置上大大提高了基于度量的方法的性能,这也验证了模糊逻辑知识确实对小样本的性能提高有所帮助。
