基于改进VSG技术双向充电桩控制策略研究

邱存勇，宋 佳，宋海亮，刘太豪

(西南石油大学电气信息学院，四川成都 610500)

随着环境污染与能源的日益紧缺，燃油汽车由于能耗高、排放高等缺点将逐渐退出市场。电动汽车由于其清洁高效的特性将逐步取代燃油汽车成为应用广泛的交通工具，发展潜力巨大。未来大规模的电动汽车同时使用时必将给电网带来一定冲击，影响电能质量。

电动汽车既可以作为储能单元储存电能，也可作为备用分布式电源为电网供能。当电网处于低谷负荷时，电动汽车作为储能单元消纳电网能量；当电网处于峰值负荷时，电动汽车作为分布式电源向电网提供能量，维持电网稳定[1-4]。分布式能源与电网之间须有一个双向变换器作为充放电接口，充放电接口的控制方式也决定了其系统的稳定性。传统控制技术常为恒功率控制、PQ 控制、下垂控制等[5]，当大规模电动汽车同时充放电时会引起电网的波动，造成电网功率失衡及频率波动，影响系统稳定性。针对以上问题，有学者将惯性思维引入变换器的控制，提出了虚拟同步机控制技术(VSG)，与传统的逆变器控制相比，VSG 控制更简单，建模容易。文献[5-6]通过将三相逆变器进行控制使其模拟同步电机的外特性，从而使逆变器具有阻尼与惯性作用。改善了系统的稳定性，但未考虑到系统的一次调频。文献[7]将VSG 算法应用于三相变换器虽然考虑了系统的一次调频，但是并未考虑到无功功率变化对三项变换器输出端电压的调节。文献[8]提出电压型虚拟同步电机控制算法，同时兼顾了电压与频率调节，但是并未考虑到系统的动态性能。

文章针对大规模电动汽车并网的背景，提出了一种基于改进虚拟同步电机控制算法，通过虚拟同步电机(VSG)将三相变换器模拟成同步电机，使其具有惯性与阻尼，缓解并网时系统产生的波动，并且通过模型预测控制算法(MPC)根据当前时刻电流值得到下一时刻电流的预测值，对下一时刻参考电流与预测电流的差值进行实时滚动优化，得到下一时刻的控制矢量，提高系统的实时动态响应，同时兼顾调压调频。该方法建模容易，精度要求不高，控制简单，增加了系统的动态性能与稳定性，提高了充放电效率。

1 控制系统整体结构

文章所提出的改进虚拟同步电机控制算法采用双层控制策略，主要由上层VSG 算法和底层MPC 控制算法构成。算法设计整体结构主要由变换器、VSG 控制模块和模型预测控制模块组成(见图1)，首先通过功率计算模块计算出所需的有功功率与无功功率参考值，通过调速器得到输入功率，经VSG 控制器得到虚拟转子的相位角θ，通过调压器可得到输入VSG 的无功电压E。通过得到的相位角θ和无功电压E经过参考电流生成模块得到参考电流在α、β轴上的分量i∗α、i∗β，再通过对下一时刻的预测电流与当前时刻的电流参考值进行对比选出最优的控制矢量信号对系统进行最优控制。

图1 控制系统整体结构框图

2 改进VSG 技术控制策略

2.1 VSG 模型的建立

2.1.1 调速器设计

系统频率的稳定是维持系统稳定运行的关键因素，在控制系统稳定性上起着至关重要的作用。调速控制器通过调整有功功率随负荷变化的差额，使系统的频率稳定，从而使系统达到稳定。根据同步电机有功-频率特性方程可以得到虚拟同步机的调速器框图如图2 所示[9]。

图2 虚拟调速器结构框图

2.1.2 调压器设计

与有功平衡相似，系统的无功功率直接影响着电网的电压稳定。因此，无功平衡也对系统稳定性起着非常重要的作用。无功平衡是指系统产生的无功功率与消耗的相等。通过模拟同步电机的下垂特性可以得到VSG 的无功电压控制框图如图3 所示[10]。

图3 调压器控制结构图

2.1.3 虚拟转子设计

根据图1 所示电路拓扑结构，虚拟同步机的转子方程可表示为[11]：

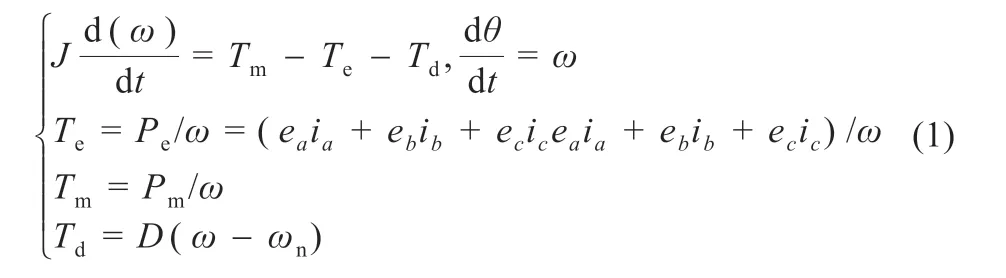
式中：Pm、Pe分别为VSG 的机械功率与电磁功率；Tm、Te和Td分别为VSG 的机械转矩、电磁转矩与阻尼转矩；J为转动惯量；ea、eb、ec为VSG 的电动势；ia、ib、ic为VSG 的输出电流；ω为VSG 的电网角速度；ωn为电网参考角速度；D为VSG 的阻尼系数；θ 为相位角；t为时间。

可将式(1)转化成式(2)：

式中：PVSG为虚拟同步机的有功功率指令。

此处引入阻尼系数和转动惯量来实现虚拟的阻尼与惯性，从而改善功率变化时频率的波动。

通过上述分析，可以得到虚拟转子角速度ω与输出有功功率之间的关系，为电流生成模块提供参考相位角θ。

2.2 参考电流生成模块

根据图1 所示电路拓扑结构可以建立变换器数学模型：

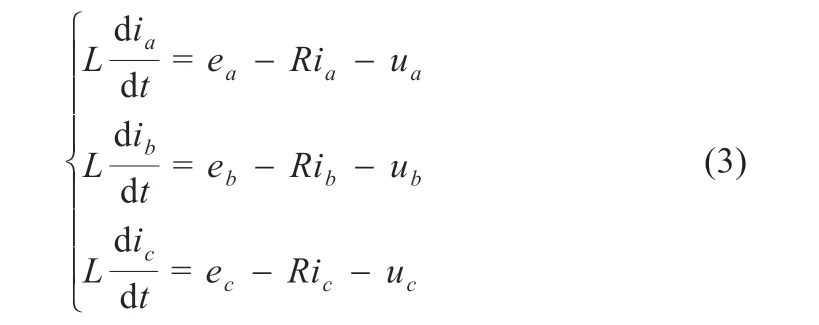
式中：L为滤波电感；R为滤波电阻；ua、ub、uc为电网电压。上述模型交流侧为时变参数，所以需要通过Clark 与Park 变换将三相电流与电压进行坐标变换，然后进行无静差控制。式(3)经Clark 变换得到两相静止坐标系下的变换器数学模型如下：

式 中：eα、eβ为 经过Clark 变 换 的VSG 电动势；uα、uβ为经过Clark 变换的电网电压。

将三相电流ia、ib、ic经Clark 与Park 变换得到两相旋转坐标系下的电流id、iq：

式中：Cabc/αβ为Clark 变换系数矩阵。

式中：Cαβ/dq为Park 变换系数矩阵。

同理可算出ud、uq如式(7)所示：

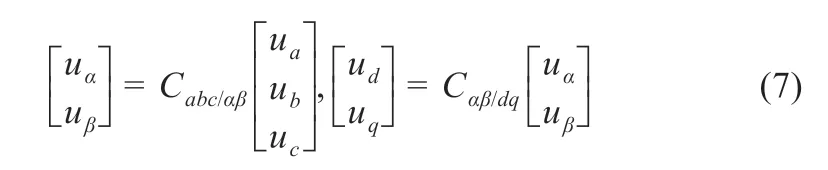
通过式(3)、(6)可推算出两相旋转坐标系下的电压参考值

式中：Kdp、分别为PI 控制器的比例和积分系数。

综上所述，通过虚拟同步机控制与电流参考生成模块可得到电动汽车充放电时的参考电流，为下层模型预测控制提供优化对象。

2.3 模型预测控制策略

相比传统虚拟同步电机矢量控制，文章引入MPC 控制算法，将VSG 输出的参考电流通过模型预测控制进行实时滚动优化，具有实时性与鲁棒性强等优势。

模型预测的目的是根据K+1 时刻的参考电流与预测电流的差值来选取最优的开关组合序列，因此首先定义开关函数为：

三相变换器有三个桥臂，因此对应八种开关组合，定义开关函数与电压矢量关系为：

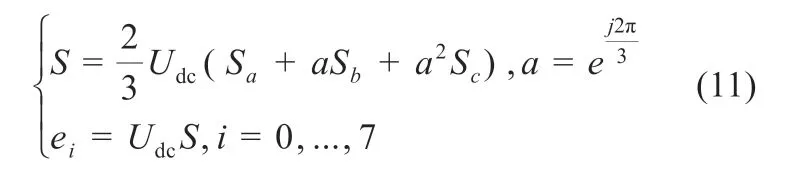
由此可以得到八种不同的电压空间矢量，由于SaSbSc=000 和SaSbSc=111 均产生的是零矢量，因此e0=e7。

将输出电压矢量变换到αβ 坐标轴：

假设系统的采样周期很小，根据前向差分原理可将逆变器模型中的微分项近似表示为[12-14]：

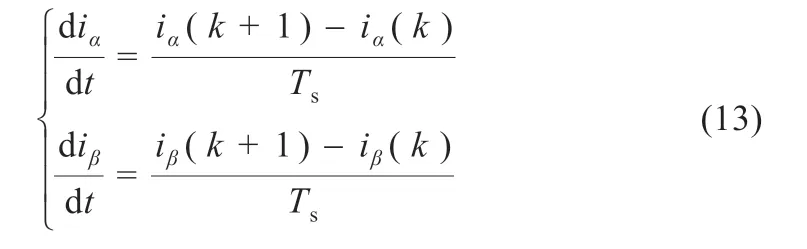
将上式代入式(7)可得电动汽车充放电电流下一时刻离散预测模型：

式中：Ts为采样周期。

根据变换器不同的开关组合状态，V(k+1)共有8 种不同的电压矢量，为使结果与预测值误差达到最小，控制性能达到最优，通过参考电流与预测电流的差值来选取一种电压矢量作为下一时刻的控制信号，在此设计其价值函数为：

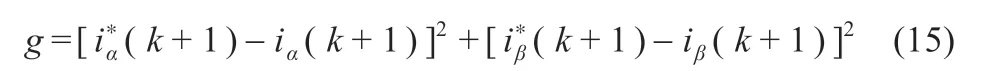
3 仿真分析

为验证文章所提控制算法的有效性，基于MATLAB R2018a/Simulink 仿真平台搭建了MPC-VSG 模型和传统VSG模型，整个系统主要由电动汽车储能系统、三相电网、双向变换器和控制系统组成，仿真算法采用ode45，J=1，D=20，KP=1，KI=200，电池满充电压为300 V，额定端电压200 V，初始剩余电量为80%，电路参数设置见表1。

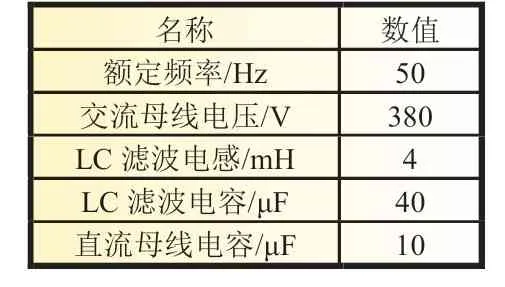
表1 电路参数

假设正方向为放电方向，断路器在t=0.5 s 时合闸，在时间1～3 s 时分别设定参考充放电功率为Pset=±2 kW，Pset=±5 kW，Pset=±10 kW。在电网频率与电网电压恒定时分别对25辆和50 辆电动汽车进行改进VSG 算法充放电仿真，仿真波形图见图4。

图4 充放电仿真波形

由仿真结果可知，由于内部频率在第2 s 和第3 s 时功率突增，系统出现波动，但很快保持到与三相电网额定频率基本一致[见图4(a)]；随着第2 s 和第3 s 的充放电功率的增加，电池的剩余电量SOC值分别逐渐提高和降低，剩余电量斜率增加，充放电速度加快[图4(b)]；在不同规模电动汽车群并网时，并网汽车数量越大，对电网的频率波动越大[图4(c)]；VSG的输出电压与电网的差值在控制器的作用下快速减小到0[见图4(d)]，从而有效地避免了并网时产生的冲击，使电动汽车通过充电桩顺利接入电网。

然后分两种情况对系统调频能力进行仿真，第一种情况设置电网频率为50 Hz，初始电压为1.02 倍基准电压，第二种情况设置电网频率为50 Hz，初始电压为0.98 倍基准电压，电动汽车剩余电量SOC值设置为80%，汽车规模设置为25辆。

从仿真结果可以看出[见图(5)]，当电网处于第一种情况时，电网电压大于额定电压，从第2 s 开始电网频率开始上升，第3 s 稳定到50.05 Hz[图5(a)]，电动汽车处于充电状态，自动从电网吸收电能，剩余电量增加[图5(b)]。当电网处于第二种状态时，电网电压小于额定电压，从第2 s 开始电网频率分别开始下降，第3 s 时稳定到49.95 Hz[图5(a)]，电动汽车处于放电状态向电网输送电能，以此来调节频率，汽车的剩余电量随之减少[图5(b)]。电网电压与输出电压的差值在0.5 s 时合闸后减小到零[图5(c)]，文章所提方法可根据当前电网状态自动调压调频，能够有效缓解系统产生的波动。

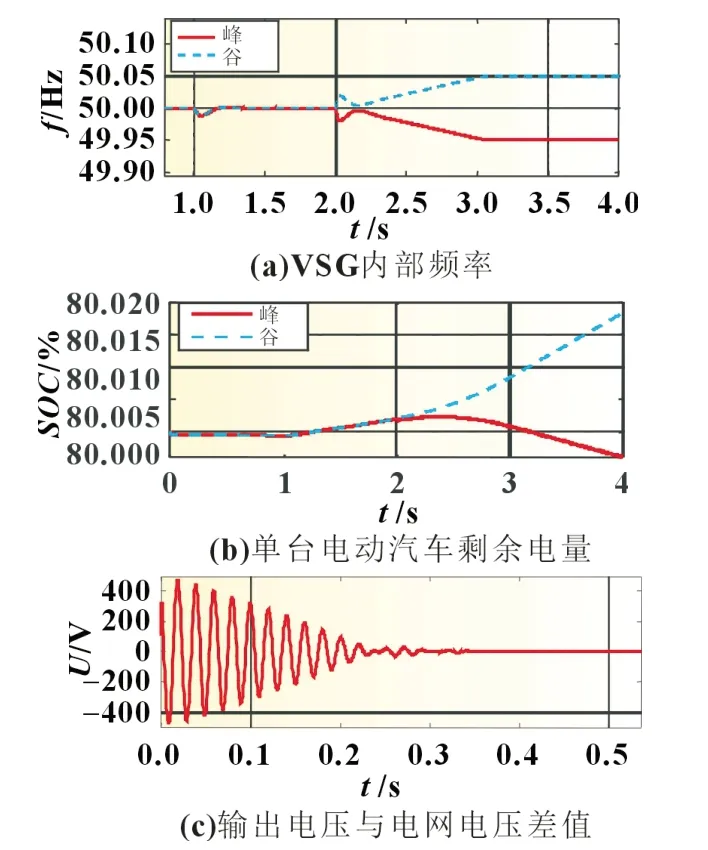
图5 两种不同情况下的电仿真波形

在同样情境下对传统VSG 算法进行仿真，在此选取两种算法充电状态的频率波形的局部放大图进行对比。由图6(a)可知，文章所提出的改进VSG 算法上升时间与调节时间明显快于传统VSG 算法，系统响应速度比较快，改进VSG 的超调量也小于传统VSG 算法，系统稳定性更高。由图6(b)可知，在第1、2 和3 s 时随着功率增加，频率波动也在增加，但改进VSG 算法的波动明显小于传统VSG 算法。

图6 充电时内部频率局部放大图对比

分别采用传统VSG 与改进VSG 充电时的网侧A 相电流的谐波分析可知(见图7)，传统VSG 的网侧电流THD=1.83%，改进VSG 的网侧电流THD=0.91%，说明采用改进VSG 的方法可以减少充电时电网产生的谐波，提高了供电质量。

图7 网侧电流谐波分析

从上述仿真结果可知，文章所提出的控制算法可以有效抑制系统波动，提高供电质量，实时跟踪系统功率变化，提高系统动态性能并且可以根据电网电压与频率调节输出，实现电网的频率调节。

4 结论

文章以基于V2G 模式的电动汽车充放电为背景，对双向充电桩提出基于改进虚拟同步机控制算法具有以下优势：

(1)电网电压低于额定电压时自动设置为放电模式向电网回馈电能，电网电压高于额定电压时自动设置为充电模式，从电网吸收电能，以此调节电网频率，减小电网波动，提高用电质量。

(2)采用模型预测控制与虚拟同步机相结合的控制算法，传统的VSG 矢量控制算法实时性与鲁棒性都不强，针对V2G模式的电网是实时变化的，模型预测控制通过建立预测模型、滚动优化及反馈校正三个环节来控制系统实时优化使输出结果与参考值接近[15]。对于电力变换器的预测控制可以看作是如何去选取一组最优的开关组合进而控制输出值尽可能去接近参考值，此方法建模直观，控制方式简单，且性能函数构造灵活，相对于传统VSG 算法，提高了系统的动态性能与稳定性。