基于改进麻雀搜索算法的MPPT方法
2021-07-29赵巧静边敦新王训栋
赵巧静,边敦新,陈 羽,王训栋,崔 帅
(山东理工大学电气与电子工程学院,山东淄博 255000)
近年来,各个国家积极开发新的可再生能源,预计到2023 年,可再生能源的使用将占据1/3,其中应用最广的是太阳能发电[1]。在现实应用中,由于自然天气等原因,部分光伏模块会被云或其他建筑物等遮挡,使得最大功率呈多峰现象[2],从而降低光伏组件的效率。
在局部阴影条件下,使用传统的粒子群优化(particle swarm optimization,PSO)算法,很大程度上会使最大功率跟踪(maximum power point tracking,MPPT)陷入局部最优,达不到全局最大功率点[3]。文献[4]采用PSO 算法与扰动观察(perturbation and observation,P&O) 法相结合,保证了系统的跟踪速率,但振荡幅度较大。文献[5]提出了粒子群算法,该算法能够精确搜索到最大功率点,但容易早熟收敛,且对于参数的要求比较高。文献[6]采用改进粒子群优化算法实现多峰值最大功率点跟踪,但适应值函数须在特定遮荫条件下才能实现,所以缺乏应用性。
麻雀搜索算法(sparrow search algorithm,SSA)是一种新型的群体智能优化算法[7],在非线性优化和动力传达机构等方面取得了良好的成就。该算法具有收敛速度快、易于实现等优点,但易陷入局部最优解。
针对以上现象,提出了一种改进麻雀搜索算法(improved sparrow search algorithm,ISSA),对原始麻雀搜索算法中的生产者和追随者的位置进行了改进。从仿真实验中可以看出,相比于PSO、SSA 算法,本文所提ISSA 算法能够快速跳出局部最优,达到最大功率点,具有较高的收敛精度和收敛速度。
1 光伏电池数学模型及输出特性
1.1 光伏电池数学模型
在光伏发电系统中,光伏电池组件是由多个串并联的光伏电池组成的[2]。光伏电池等效模型如图1 所示。
由图1 可得光伏电池的输出表达式为:

图1 光伏电池等效模型

式中:Iph为光生电流;I0为反向饱和电流;Rs、Rsh分别为串并联电阻;q为电子的单位电荷;A为p-n 结的理想因子;θ为单元阵列的温度;k为玻尔兹曼因子;V为光伏电池输出电压。
当光伏电池处于最大功率点处时,V=Vm,I=Im,在开路状态时I=0,V=Voc。可得在标准辐照强度和标准外界温度条件下的输出电流,但在一般情况下并不能直接使用,修改后的特性曲线公式为:

式 中:Isc为 短 路 电 流;S为 光 照 强 度;Sr=1 000 W/m2;a=0.002 5/℃;θa为环境温度;θr=25 ℃。

式中:Im为光伏电池处于最大功率点处时的电流。

式中:Voc为开路电压;c=0.002 8/℃;e=2.718 3;b=0.5。

式中:Vm为光伏电池处于最大功率点处时的电压。
1.2 光伏电池的输出特性
在光照不均匀的情况下,光伏阵列的输出特性是非线性的,会呈现多峰值现象[8]。现将三个光伏电池进行串联研究,设光伏电池的温度均为标准外界温度25 ℃。在模式1 下,光照强度为S1=1 000 W/m2、S2=800 W/m2、S3=600 W/m2;在模式2下,光照强度为S1=800 W/m2、S2=600 W/m2、S3=400 W/m2。在两种模式下的P-V特性曲线如图2 所示。
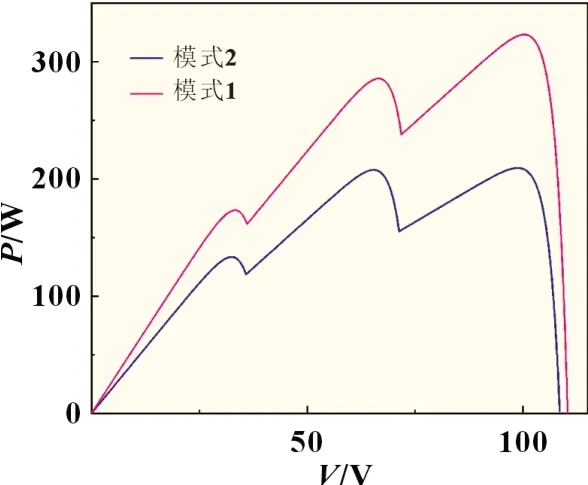
图2 光伏列阵在局部阴影下的特性曲线
2 不同麻雀搜索算法
2.1 麻雀搜索算法
在麻雀觅食的过程中,可将麻雀分为发现者和追随者,同时在种群中还存在捕食者[7]。发现者在群体中的职责是搜寻食物找到充足的食物资源和为种群提供觅食的区域、方向;追随者通过追随发现者获得食物[7]。
麻雀搜索算法在全局搜索中具有多种优点:搜索精度高、收敛速度快、稳定性好等。在麻雀搜索算法中,适应度值好的发现者在寻找食物的过程中会优先得到食物,同时为其他的追随者提供觅食的方向。所以,生产者的搜寻范围会大于追随者的搜寻范围[7]。生产者的位置更新公式为:
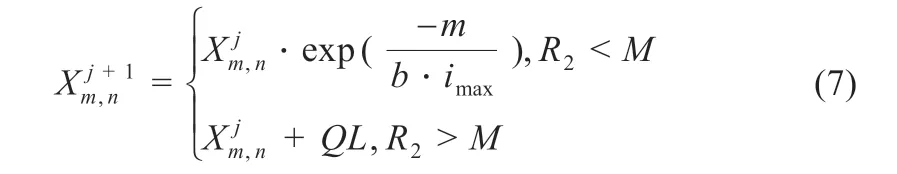
式中:j为当前的迭代次数;m为第几个麻雀;n=1,2,3,...,d,其中d为待优化问题变量的维数;imax为最大迭代次数;Xm,n为第m个麻雀在第n维的位置信息;b为在0~1之间的一个随机数;R2(R2∈[0,1])为预警值;M(M∈[0.5,1])表示安全值;Q为一个随机数服从正态分布;L为1 行d列的矩阵,矩阵内的元素全都为1。当R2
追随者的位置更新公式为:

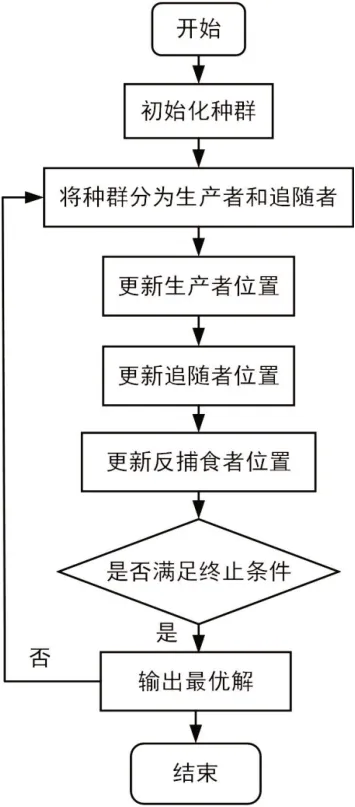
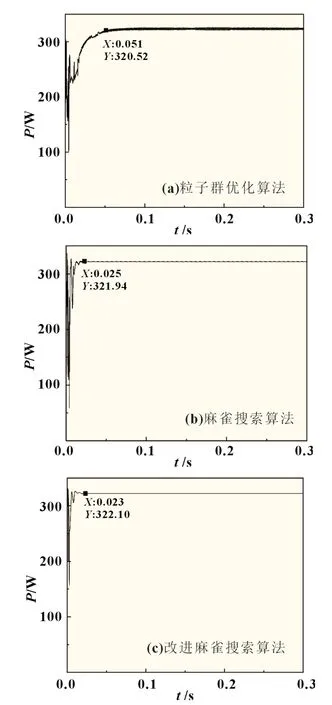
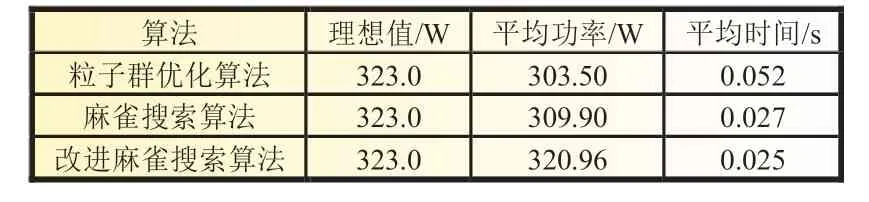
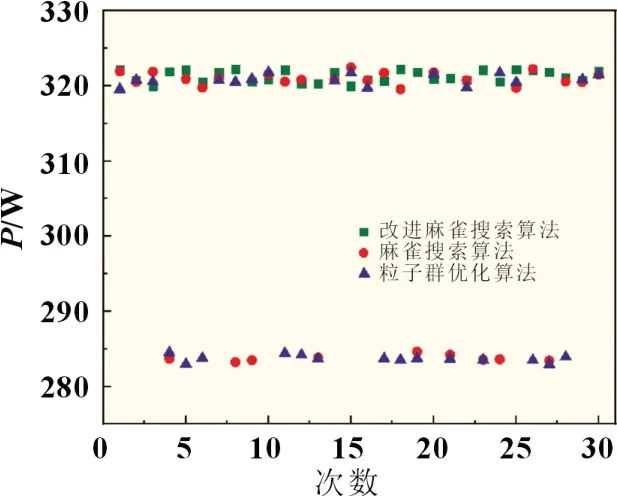
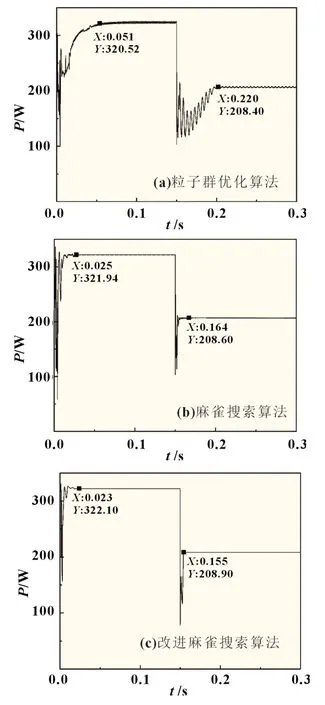
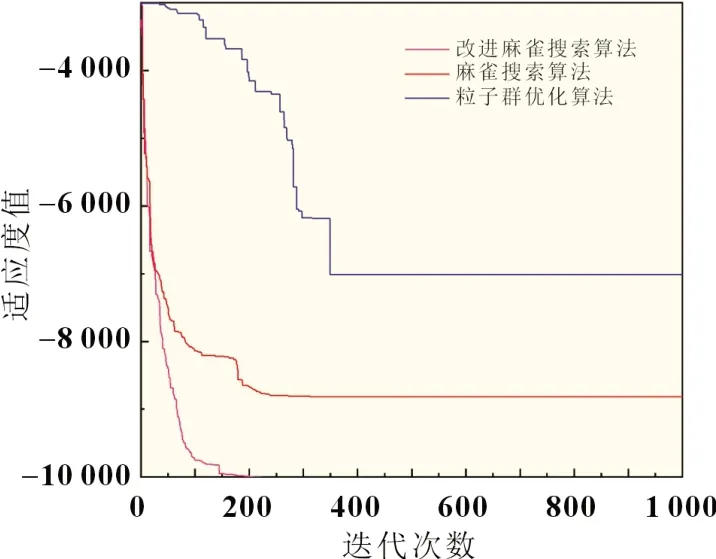
式中:Xw为在当前维度空间中种群的最差位置;XP为目前发现者所占据的最优位置;A为一个1 行d列的矩阵,矩阵内的元素为1 或者-1;AT表示矩阵A的转置。当m>N/2,表示第m个适度值低的追随者所获得的食物很少,为得到更多的食物必须到别的区域觅食,其飞往的位置符合标准正态分布随机数。当m 反捕食者的位置更新公式: 式中:β为标准正态分布的一个随机数;Xbest为当前的全局最优位置;K为在区间[-1,1]内的随机数;δ为一个常数其数值非常小,目的是防止分母为零没有意义;fm为当前个体的适应度值;fg为目前全局最佳适应度值。当fm>fg时,个体会向最佳位置方向移动;当fm=fg时,个体会移动到该位置附近。 麻雀搜索算法在全局搜索中,生产者的预警值在小于安全值时,由指数函数y=exp(-x)的基本图像可知X越小取1 的概率越高,随着X的增大其值收敛于零。因此麻雀搜索算法在求原点附近的最优解问题时,其收敛性非常快,远快于其他算法。但是当求解问题的最优解距原点较远时,其性能会有所下降,容易陷入局部最优。其次,追随者在m 反捕食者的位置简化公式: 粒子的位置X表示光伏阵列的参考电压,目标函数f表示光伏阵列的输出功率,具体流程如图3 所示。 图3 ISSA算法流程 步骤如下: (1)对麻雀搜索算法的参数进行初始化,设置种群总数、最大迭代次数、变量维数、生产者和追随者的数量、随机生成个体的初始位置; (2)将种群按一定比例划分为生产者和追随者,个体随机选择自己的身份; (3)采集电压和电流,根据目标函数确定每一个个体的适应度值,保存目前最佳位置和最差位置; (4)根据式(10)~(12)分别更新生产者、追随者、反捕食者的位置; (5)计算当前最佳目标函数值fmax,更新最优值和个体最佳位置,若f>fbest,则Xbest=X,fbest=f; (6)结束算法,输出目标函数的最优解。 为了验证所提改进麻雀搜索算法的优越性,分别采用PSO、SSA 和ISSA 算法在MATLAB/Simulink 中建立光伏系统MPPT 仿真模型。仿真模型主要包括四大块:光伏组件、最大功率跟踪模块、Boost 模块、PWM 模块。通过最大功率跟踪模块得到最大功率点处电压,与C1两侧电压作差,再经过PWM模块得到IGBT 的导通信号,使输出电压保持在全局最大功率点电压处,从而得到最大输出功率。仿真参数为:温度θ=25 ℃,直流母线电容C2=100 µF,滤波电容C1=50 µF,电感L=10 mH。PSO 算法参数为:n=50,最大迭代次数为1 000,惯性因子w=0.7,学习因子c1=c2=1。 采用光伏系统MPPT 仿真模型,在模式1 中,分别采用粒子群优化算法、麻雀搜索算法和改进麻雀搜索算法进行仿真,仿真结果分别如图4 所示。 图4 静态光照条件下功率追踪曲线 从图4 静态光照条件下功率追踪曲线可以看出PSO 算法在0.051 s 左右时功率趋于稳定,稳定在320.52 W 附近,与理论值323 W 相差2.48 W,追踪精度为99.2%。稳定后输出功率振荡较大,振荡幅度约为±3 W,在很大程度上降低了发电效率;SSA 算法在0.025 s 时功率趋于稳定,达到全局最大功率约为321.94 W,与理论值相差1.06 W,追踪精度为99.67%,振荡幅度较小约为±1 W;ISSA 算法在0.023 s 时追踪到最大功率,约为322.10 W,能量损耗最小,与理想值323.00 W 相差0.90 W,追踪精度可达99.7%。 由于算法在进行迭代寻优过程中具有随机性,这里将PSO、SSA 和ISSA 算法分别进行30 次实验[8]。三种算法的功率分布如图5 所示,并在表1 中记录三种算法的理想值、平均功率和平均时间。 表1 三种算法的性能比较 图5 功率分布 从图5 功率分布图可以看出,在30 组实验测试中PSO 算法有14 次陷入局部最优;SSA 算法有9 次陷入局部最优;而ISSA 算法均能找到最大功率点。可以看出,PSO 和SSA 算法的全局搜索能力相对较弱,容易陷入局部最优;ISSA 算法的全局搜索能力较强,能够及时跳出局部最优解。从表1 三种算法的性能比较可以得到,改进麻雀搜索算法无论在追踪精度方面还是收敛速度方面都优于粒子群优化算法和麻雀搜索算法,证明了改进麻雀搜索算法的优越性。 为了验证ISSA 算法在动态光照条件下的追踪效果,在0.15 s 时将光照强度由模式1 突变为模式2,分别对PSO、SSA和ISSA 算法进行仿真实验,实验结果如图6 所示。 图6 动态光照条件下功率追踪曲线 从图6 中可以看出,三种算法在0.15 s 光照突变后都能达到最大功率点附近。PSO 和SSA 算法在达到最大功率时,震荡幅度较大,收敛速度较慢;ISSA 算法达到稳定后,振荡幅度较小,且具有较高的收敛精度和收敛速度。 采用两种测试函数来对粒子群优化算法、麻雀搜索算法和改进麻雀搜索算法进行比较,如图7 和8 所示。同取最大迭代次数为1 000,维度d=2,n=100,c1=c2=2,惯性因子w=0.9。在进行迭代寻优测试时,为得到数据的准确性,分别对粒子群优化算法、麻雀搜索算法和改进麻雀搜索算法进行了30 组实验,记录三种算法在达到稳定时所需的时间。 图7 所示迭代寻优效果选取的测试函数是最优解收敛于原点的。从图中可以看出SSA 算法和ISSA 算法都能达到理论最优值,而PSO 算法陷入了局部最优。PSO 算法在达到稳定时所用时间为2.370 s,SSA 算法所用时间为1.675 s,ISSA算法所用时间为1.344 s,ISSA 算法相比PSO 算法用时缩短了43.29%,相比于SSA 算法缩短了19.76%。 图7 迭代寻优效果图 图8 中迭代寻优效果选取的测试函数是最优解远离原点的。从图中可以看出,在进行迭代寻优测试时,ISSA 得到的最优值为-10 021.5,SSA 得到的最优值为-8 817.3,PSO 得到的最优值为-7 014.5。在进行30 组实验后,发现改进麻雀搜索算法无论在收敛时间方面还是收敛精度方面都优于其他两种算法。 图8 迭代寻优效果图 提出了一种改进麻雀搜索算法,根据算法性能测试表明,该算法具有较高的收敛速度和收敛精度。将其应用在光伏系统最大功率跟踪模块,在MATLAB/Simulink 建立仿真模型,并与PSO 和SSA 算法进行仿真对比。根据实验结果可知,改进麻雀搜索算法能够快速准确地找到最大功率点,减小输出功率曲线的振荡幅度,提高光伏发电系统的输出效率。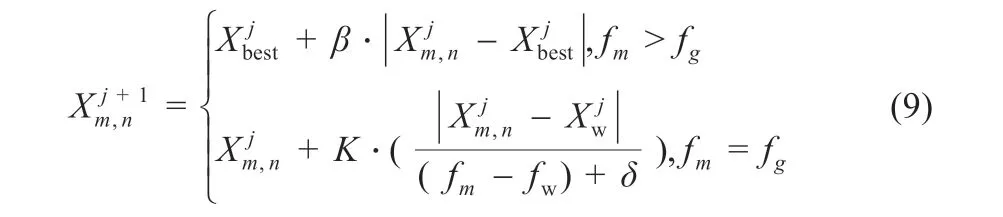
2.2 改进型麻雀搜索算法

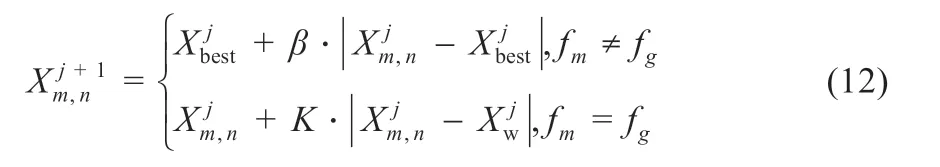
3 仿真分析
3.1 静态仿真分析
3.2 动态仿真分析
4 算法性能测试

5 结论
