山区隧道基于围岩稳定的合理开挖进尺分析
2021-07-29李官群田庆
李官群, 田庆
(1.保靖县交通运输局, 湖南 保靖 416000;2. 保靖县农村交通建设技术咨询服务站, 湖南 保靖 416000)
新奥法操作简单,安全高效,超过60%的隧道采用该方法施工。对于不同的地质条件,合理控制开挖进尺是保障隧道施工安全与进度的关键。施工中通常根据隧道围岩实际情况,将规范与实践经验相结合确定开挖进尺。在理论研究方面,石先火等基于简仓理论分析隧道开挖进尺对预留核心土长度和岩堆体物理参数的敏感性,结果表明预留核心土能提高掌子面的稳定性,开挖进尺对围岩黏聚力敏感;李辉等推导软岩浅埋隧道开挖进尺计算公式,认为隧道开挖进尺不仅要保证拱顶稳定,还要保证掌子面稳定,由二者共同决定;李现宾等建立某公路隧道三维有限元模型,分析多煤层夹断层影响下隧道开挖进尺,得出开挖进尺并非越小越好,隧道开挖对围岩的扰动作用使围岩变形增大,而开挖进尺过大,开挖后沉降已远远超过扰动作用下沉降;郑泽源基于简仓理论和Horn模型推导水下隧道掌子面稳定的理论计算公式,并把理论计算结果与有限元模型分析结果进行对比,验证理论的正确性。该文从普氏平衡拱理论和Horn模型出发,引入围岩稳定安全系数,推导基于围岩稳定的合理开挖进尺计算方法,并结合屋场坪隧道现场施工情况相互比较、相互印证,为隧道安全施工提供理论支持。
1 普氏平衡拱理论
1.1 失稳机理
普氏平衡拱理论将围岩看作松散体,隧道开挖后,围岩具有一定自稳能力,即使塌落,也不会无限发展,塌落终止后,围岩的稳定界面和围岩压力近似于拱形,通常称为自然平衡拱。自然平衡拱具有一定的自稳能力,但只能在短时间内保持平衡,若时间过长或受到扰动,新的变形就会产生,达到新的稳定平衡状态,从而形成新的自然平衡拱,甚至坍塌。
普氏平衡拱理论认为,处于二次应力状态的围岩顶部出现拉应力,若拉应力未超过围岩的抗拉强度,则围岩稳定;若拉应力超过围岩的抗拉强度,则围岩塌落。
在此基础上,普氏平衡拱理论作出如下假设:1) 隧道开挖后,松散的围岩仍具有一定的黏聚力;2) 围岩压力仅是自然平衡拱内的岩体自重;3) 形成的自然平衡拱只受压应力的作用;4) 引入岩石坚固系数fkp表示岩体的强度,它是关于围岩正应力σ的函数,而不是通过岩体的特征参数计算得出。
普氏平衡拱理论的前提是隧道上部岩体能自然形成压力拱,这就要求岩体具有相当的稳定性和足够的厚度,能否形成压力拱是能否采用普氏平衡拱理论计算的关键。具体要求如下:1) 普氏平衡拱理论将岩体看作散体,适用于断裂破碎带或强风化岩体;2) 明挖法施工的隧道不能采用普氏平衡拱理论计算;3) 岩体坚固系数fkp<0.8,且隧道顶部至地面的距离不能达到压力拱高度的2倍或小于压力拱跨度的2.5倍时,均不能采用普氏平衡拱理论计算;4) 坚固系数fkp<0的软土体,如淤泥、粉砂土、粉质黏土、轻亚黏土和饱和软黏土,由于不能形成压力拱,也不能采用普氏平衡拱理论计算。
1.2 理论计算
如图1所示,假设拱上部荷载为均布荷载p,拱脚所受水平推力为H、竖向力为V,拱顶所受水平推力为T,拱矢高为h,拱顶至拱脚的水平距离为b,围岩重度为γ。根据普氏平衡拱理论中自然平衡拱只受压不受拉的基本假设,在拱轴线上,外力对任一点的弯矩M(x,y)为零,即:
(1)
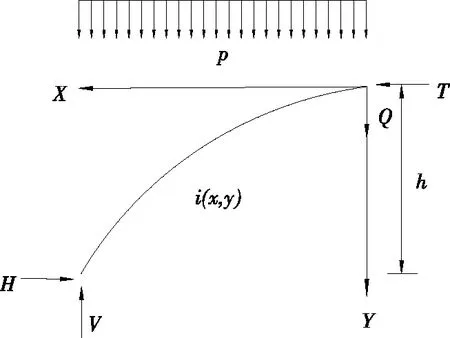
图1 基本结构示意图
在拱脚处,x=b,y=h,式(1)变为:
(2)
拱脚在水平推力T的作用下很容易失稳,为避免出现拱圈失稳情况,需使H≥T。拱脚的横推力H为:
H=fkpbp
(3)
式中:fkp为普氏岩石坚固系数,通常把岩石单轴极限抗压强度Rc的1/10作为岩石的坚固系数,即fkp=Rc/10。
联立式(2)和式(3),由H≥T得:
(4)
式(4)化简得:
(5)
隧道任意一点的围岩压力q为:
(6)
围岩总压力W为:
(7)
假设隧道开挖后不发生坍塌,围岩在黏聚力c作用下处于稳定状态,则围岩自重等于黏聚力。
W=2cb
(8)
联立式(7)和式(8),得:
(9)
式(9)化简得:
(10)
在实际工程中,为确保隧道施工安全,引入安全系数K,隧道开挖进尺为:
(11)
2 Horn模型
2.1 失稳机理
Horn模型以简仓理论和摩尔-库伦准则为理论基础,以掌子面失稳为条件,针对软岩隧道台阶法开挖方法计算隧道开挖进尺。Horn模型由隧道掌子面失稳前面的楔形体及其上方的柱体组成,并假定隧道开挖面积与正方形大致相等。当掌子面上方土体松动变形时,楔形体受到压力作用,通过极限平衡理论计算掌子面的支护力(见图2)。
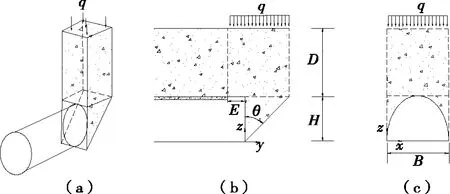
E为隧道开挖进尺;H为隧道开挖高度;D为隧道顶部至地面的高度;θ为楔形体纵向滑动面的倾斜角;B为隧道开挖宽度
如图3所示,掌子面的失稳形式表现为掌子面正前方支护能力不足,即掌子面前方的支护力S≤0。工程实际中,支护力一般表现为掌子面喷浆、预留核心土或正向锚杆等支护作用。

G为楔形体的自重作用;V为柱体岩土发生松动或变形对楔形体的竖向压力作用;T、N分别为楔形体滑动面上剪力和法向力;Ts、Ns分别为楔形体侧面上剪力和法向力
根据摩尔-库伦准则对楔形体滑动面进行受力分析,建立以下平衡方程:
(12)
式中:φ为围岩内摩擦角。
根据极限平衡理论对整个楔形体进行受力分析,分别在楔形体方向和法线方向建立平衡方程,并消去T、N,则式(12)变为:
(13)
楔形体的自重G为:
G=0.5γBH2tanθ
(14)
提取式(13)等式右边第一部分为F1,表示作用于掌子面上的推力[见式(15)]; 提取等式右边第二部分为F2,表示掌子面上的阻力[见式(16)]。如果支护力S0≤0,则掌子面稳定。掌子面稳定性系数见式(17)。
(15)
(16)
(17)
2.2 竖向力V的计算
由简仓理论得柱体对楔形体的压应力为:
(18)
A=B(Htanθ+E)
(19)
V=Aσv
(20)
(21)
U=2(B+Htanθ+E)
(22)
式中:K0为侧压力系数;q为地面荷载;A为柱体的横断面面积;U为柱体的横断面周长。
2.3 侧向剪力Ts的计算
根据摩尔-库伦准则,楔形体两侧任意一点的剪应力为:
τ(y,z)=c+σx(y,z)tanφ
(23)
σx(y,z)=Kaσz(y,z)
(24)
式中:σx(y,z)为侧滑动面水平方向的正应力;σz(y,z)为侧滑动面竖直方向的剪应力;Ka为考虑开挖深度E影响的系数,取Ka为主动侧压力系数。
如图4所示,假定楔形体的竖向应力沿深度线性分布,则:
(25)
式中:z为沿楔形体竖直方向的高度。
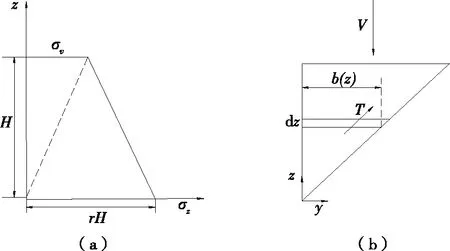
图4 楔形体竖向力分析假定示意图
联立式(23)~(25),得到剪应力与楔形体高度的变化关系:
(26)
沿楔形体高度对剪应力积分,得到楔形体的侧向剪力:
(27)
联立式(26)和式(27),得:
(28)
根据上述分析,基于Horn模型,隧道掌子面稳定性系数K是与围岩破裂角θ和开挖进尺E相关的双重变量函数。为简化计算,对于软岩隧道,将围岩破裂角θ简化为θ=45°-φ/2,即可得到不同开挖进尺所对应的掌子面的稳定性安全系数。
3 工程实例
屋场坪隧道位于湖南省保靖县,属于丘陵地貌。隧道围岩地质为第四系与寒武系娄山关群中风化白云岩,软岩,岩体松散、破碎,围岩等级为Ⅴ级。隧道全长818 m,为直线隧道,横穿2个岩层断裂带。采用新奥法施工,按上下台阶开挖。
该隧道围岩具有一定自稳能力,围岩参数和地质情况均满足普氏平衡拱理论的要求,普氏平衡拱理论适用于屋场坪隧道开挖进尺计算。Horn模型基于简仓理论和摩尔-库伦准则,以掌子面前方的支护能力体现隧道掌子面是否失稳来确定隧道开挖进尺,在力学分析上可行,同样适用于屋场坪隧道新奥法施工情况。计算参数见表1。

表1 隧道开挖进尺计算参数
对于松散、破碎的白云岩,很难通过试验得到其极限单轴抗压强度Rc,采用文献[3]中计算岩石坚固系数的近似方法fkp=tanφ。为保证隧道施工安全,一般取稳定性系数为2,则由普氏平衡拱理论计算隧道开挖进尺为:
与普氏平衡拱理论相比,Horn模型的计算方法较复杂。把隧道参数输入Excel,编辑理论计算公式,以开挖进尺为自变量(步长为0.2)、围岩稳定性系数为因变量,得到一组离散的点(见图5)。由图5可知:围岩稳定性系数取2时,基于Horn模型计算的开挖进尺为1.095 m,基于普氏平衡拱理论计算的开挖进尺为1.205 m,两者计算结果较接近。
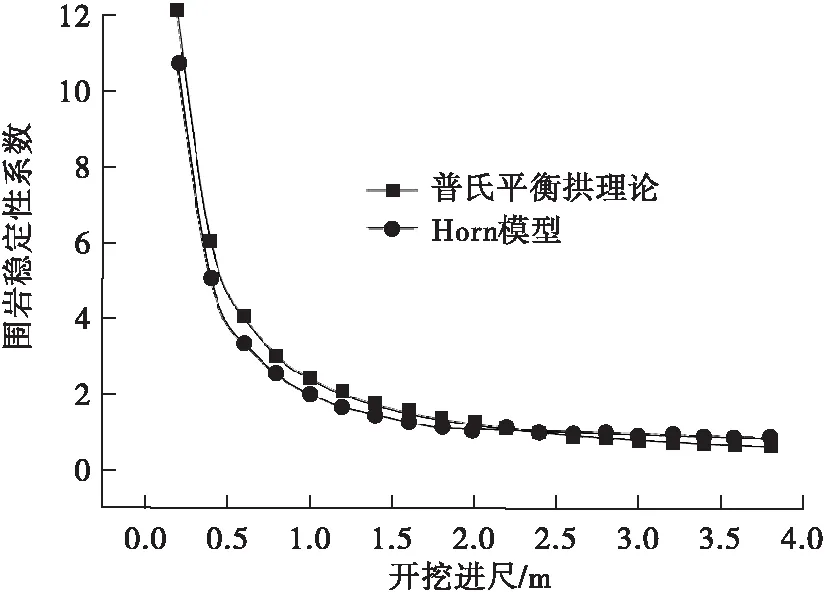
图5 围岩稳定性系数与开挖进尺的关系
屋场坪隧道施工过程中,为满足安全和规范要求,开挖进尺取一榀钢架的距离,即0.75 m。结合上述理论计算,一榀钢架的距离作为Ⅴ级围岩的开挖进尺足够安全。
4 结论
(1) 围岩稳定性系数取2时,基于普氏平衡拱理论计算的开挖进尺为1.205 m,基于Horn模型计算的开挖进尺为1.095 m。屋场坪隧道围岩情况较差,出于安全考虑,开挖进尺不得超过1 m。根据规范要求,对于Ⅴ级围岩隧道,开挖进尺取一榀钢架的距离,即0.75 m。
(2) 基于普氏平衡拱理论的计算公式,围岩稳定性系数与开挖进尺成反比例关系;基于Horn模型计算公式,两者并非严格意义上的反比例关系。2种理论都服从“开挖进尺越大,围岩稳定性系数越小”的观点。对于两台阶施工的隧道,不同的隧道断面尺寸,不同的围岩参数,其反比例系数不同,需具体情况具体分析。
(3) 普氏平衡拱理论仅考虑围岩的物理特性,没考虑隧道埋深的影响,仅对围岩能否形成自然平衡拱有较高要求,计算方法简单;Horn模型计算公式较复杂,既适用于浅埋隧道,也适用于深埋隧道。
