考虑V形冲沟三维效应的高填路堤变形特性研究

卞正荣

(上海隧道工程质量检测有限公司， 上海 201109)

山地丘陵地区地质复杂、地形起伏多变，高填路堤建设与运营期的变形特性对工程建设安全与质量有着重要影响。许多学者通过数值模拟和现场监测等方法对复杂地形因素下高填路堤变形规律展开了研究，如Anand J.等依托克莱伯恩市67号公路工程，基于双曲线模型对EPS土工泡沫塑料路堤进行沉降监测，并通过数值模拟合理预测路堤变形；侯亚玲等针对山西某黄土填料高填路堤，通过室内试验，结合二维有限元计算与现场实测数据比较分析，提出路堤沉降计算方法；李占锋以西北地区某山区高速公路为对象，结合现场实测数据和有限元法对不同高填土路基沉降影响因素进行分析，研究高填路基沉降变化特征；孙笑等通过对某高填路堤不同断面的二维数值模拟，得到典型断面高填路堤的沉降变形规律，并分析了黏土路基经过石灰土换填后的沉降变形情况；Wu P.等基于UH模型，以OCR为控制参数建立软弱地基岩土层数值模型，研究统一硬化模型下土石混合体的沉降变形；李忠友等借助三维有限元模拟，对某高填路堤及其支挡结构进行数值模拟；丁静声等基于强度折减法，对不同地形条件下V形冲沟路堤进行稳定性分析，认为该类路堤的三维效应不可忽略；徐佩华等对折线地基上高填石路堤的变形和稳定性进行三维数值仿真，分析高烈度区浸水高填石路堤变形规律；薛新华等以成昆(成都—昆明)线攀枝花南站昔格达层高填方路堤工程为依托，利用ABAQUS软件建立三维整体有限元模型，分析分层填筑中路堤的沉降变形规律。若考虑高填路堤所在地形的三维效应，高填路堤将呈现独特的变形特性，但目前对这类问题的研究尚不完善。该文以杭绍台(杭州—绍兴—台州)高速公路(台州段)扩建工程为依托，通过正交试验，考虑V形冲沟三维效应，对高填路堤建设期的沉降变形与侧移变形展开研究，为V形冲沟条件下高填路堤设计和施工提供借鉴。

1 V形冲沟条件下高填路堤变形特性

1.1 工程概况

杭绍台高速公路(台州段)地处东南沿海，为山岭重丘区，属东南亚热带气候，区内植被茂密，雨水充沛。线路呈南东-北西向展布，由东向西穿过博平岭。总体地势东南低、西北高，海拔为110～310 m，高程最大为340 m，海拔最低处约60 m，相对高差一般为40～190 m。全长27.7 km，为双向八车道，设计时速80 km/h。考虑挖填方平衡问题，线路共设计20余处高填路堤段，途经多处V形冲沟等特殊地形。

1.2 V形冲沟条件下高填路堤数值模型

以ZK64+200—800穿越某小型V形冲沟的典型高填路堤为工程原型，在FLAC3D数值平台上对其填筑过程展开数值模拟，探讨V形冲沟条件下高填路堤的变形特性。数值模型见图1，其中x轴为线路延展方向，总长220 m；y轴为V形冲沟纵深方向，总宽95 m；z轴为竖直方向，总高64 m。数值模型从下到上依次为深部地层(中风化花岗岩)、浅部地基(强～全风化花岗岩残积土)、路堤本体(残积土+砾石的混合填料)。路堤填筑前，将冲沟坡面上的虚土清理干净，数值模拟中可认为路堤本体与浅部地基是紧密连续的(无需采用接触面单元)。模型共包括37 320个实体单元、40 944个节点。模型顶面与路堤本体取自由边界，前后面与侧面边界采用法向约束，底面边界设置为固定约束。

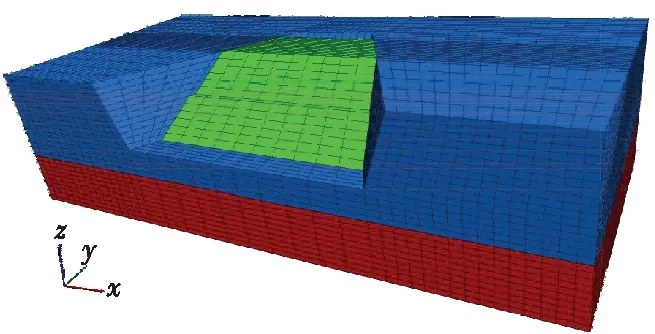
图1 V形冲沟条件下高填路堤数值模型

岩土体均采用MC本构模型，根据相关设计文件，深部地层、浅部地基及路堤本体的主要物性参数见表1。

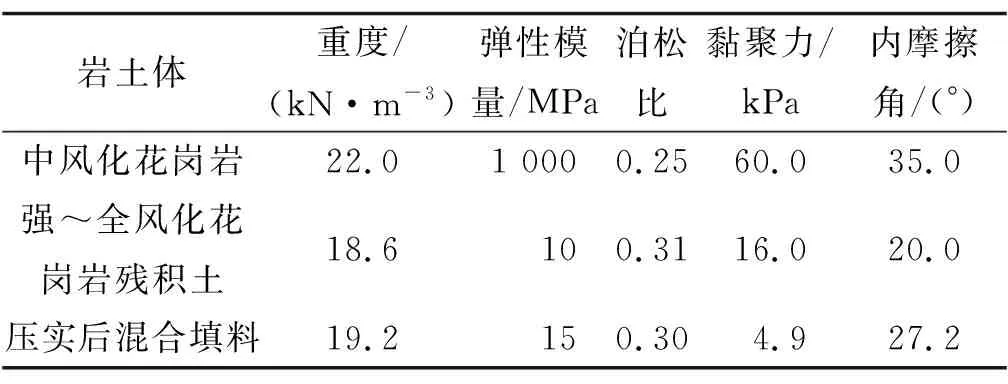
表1 岩土体的主要物性参数

1.3 工况及监测点

路堤本体总计填高24 m，按照每层堆填2 m并反复压实，自下而上共计12种工况。在路堤中心沿高程布置12个测点，观察各分层沉降变形(z向位移)随施工步的发展规律；在路堤坡面沿高程布置12个测点，观察各分层侧向变形(y向位移)随施工步的发展规律(见图2)。

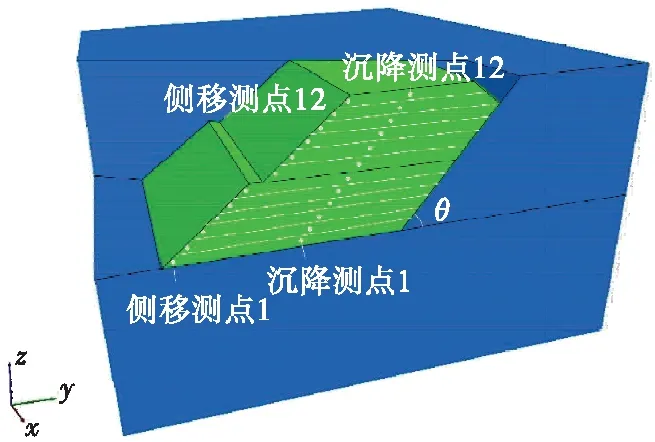
图2 测点布置示意图

1.4 高填路堤变形特性分析

根据数值模拟结果，得到典型V形冲沟条件下高填路堤分层沉降、分层侧移随施工步的发展规律(见图3、图4)。

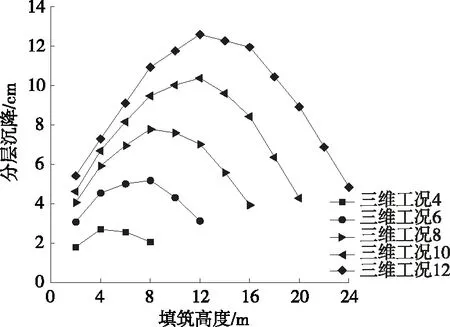
图3 高填路堤分层沉降

图4 高填路堤分层侧移

由图3、图4可知：路堤分层沉降与分层侧移均随施工步(填筑高度)不断增大，且沿高程方向均呈现中间大、两头小的发展形态，与已有结论一致。路堤中部既下伏有较厚的可压缩土层，又上覆有较大的堆填荷载，全部填筑完毕后，最大分层沉降δmax发生在路堤中部，约为12.6 cm，各分层平均沉降¯δ约为9.4 cm；最大分层侧移ηmax发生在路堤中下部，约为2.5 cm，各分层平均侧移¯η约为1.6 cm。

1.5 与二维地形的对比

若不考虑V形冲沟的三维效应，选取冲沟中心截面(图2中测点布设所在截面)按二维平面应变假定建立数值模型(见图5)，模型共计7 040个实体单元、8 404个节点，其地层及主要物性参数、模型边界条件、工况与监测点布设等均与前述相同。

图5 二维条件下高填路堤数值模型

根据数值模拟结果，对二维与三维条件下路堤分层沉降及分层侧移进行对比，结果见图6、图7。

图6 二维与三维条件下高填路堤分层沉降对比

图7 二维与三维条件下高填路堤分层侧移对比

由图6～7可知：二维条件下高填路堤的分层沉降及分层侧移规律与三维条件下基本一致，数值比三维条件下分别大3%～5%和5%～10%。

2 地形因素对高填路堤变形特性的影响

2.1 地形影响因素

根据V形冲沟的地形特点，其三维特性主要表现在开口角度α、冲沟侧坡坡度β、冲沟背坡坡度θ及沟谷均宽W四方面(见图8)。各因素对高填路堤变形的影响不同，下面通过正交试验分析各地形因素对高填路堤变形特性的影响。

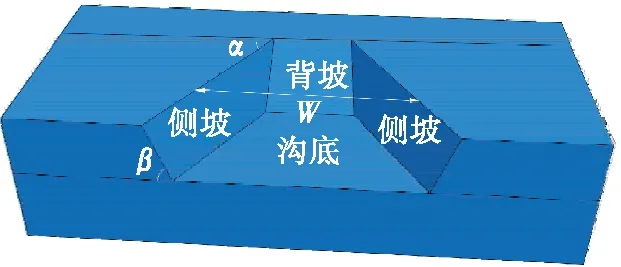
图8 V形冲沟的地形因素

2.2 正交试验设计

将V形冲沟的4个地形因素即开口角度、冲沟侧坡坡度、冲沟背坡坡度、沟谷均宽分别命名为因素A、B、C、D，每个因素设置3个水平，采用正交设计方案L9(34)，试验参数见表2。据此建立不同地形条件下高填路堤三维数值模型，其地层及主要物性参数、模型边界条件、工况与监测点布设等均与前述相同。对上述9个试验的数值模拟结果进行分析，以高填路堤分层沉降和分层位移为主要关注点，进行地形影响因素敏感性分析。

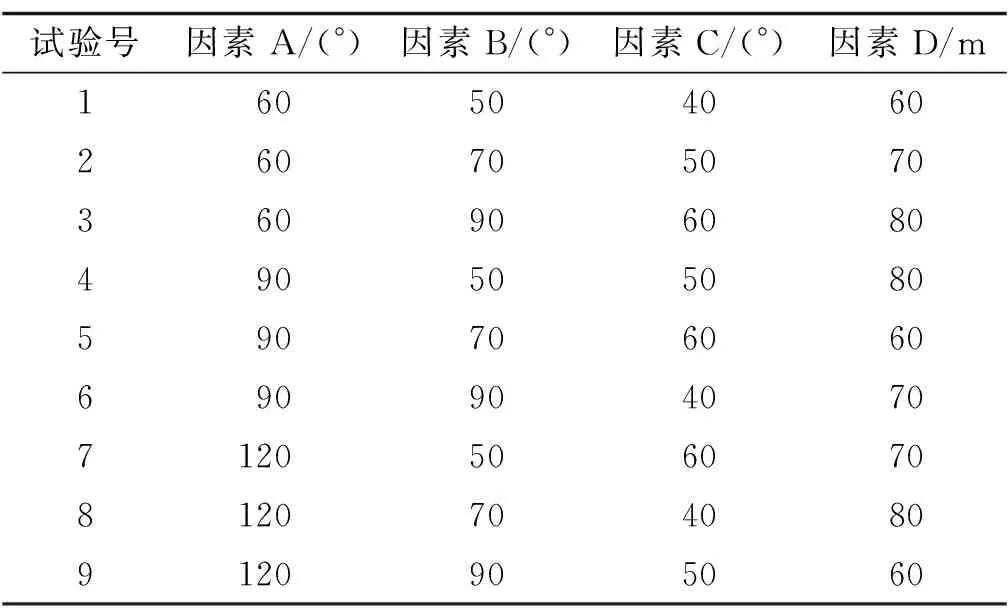
表2 正交试验设计表L9(34)

2.3 地形因素对分层沉降的影响分析

根据数值模拟结果，进行分层沉降极差分析(见表3)，各因素对最大分层沉降和平均分层沉降影响的直观分析见图9、图10。从图9、图10可看出：各地形因素对高填路堤最大分层沉降δmax影响的敏感性依次为D>B≈C>A，对平均分层沉降¯δ影响的敏感性依次为D>B≈A>C。

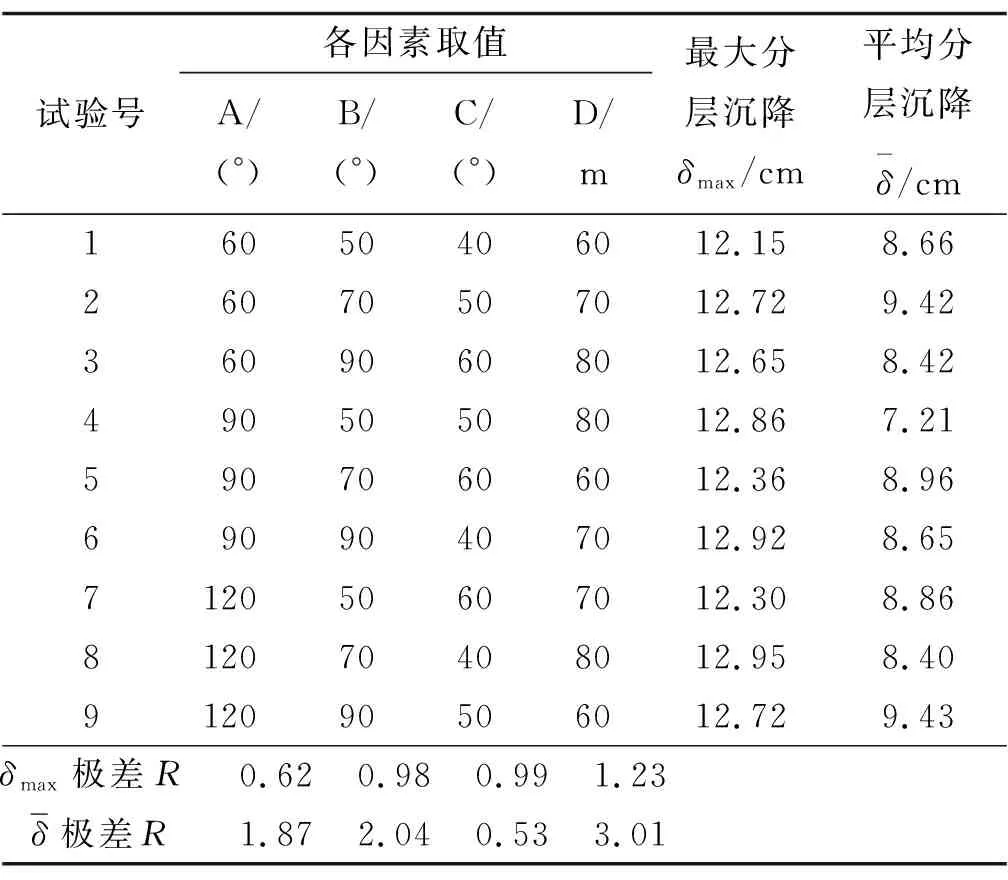
表3 分层沉降极差分析

分层沉降的方差分析见表4、表5。在置信水平α=0.05的条件(因素显著性临界值为19.0)下，对于最大分层沉降，各因素影响均不显著；对于平均分层沉降，因素D的影响显著，因素A、B、C影响不显著。与极差分析结果一致。

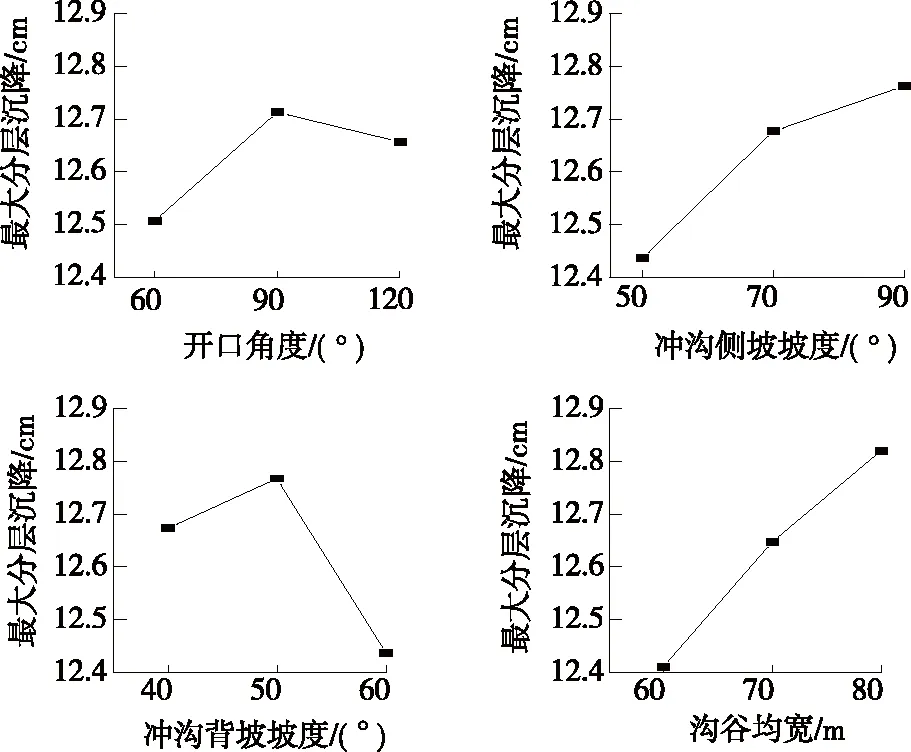
图9 地形因素对最大分层沉降影响的敏感性分析

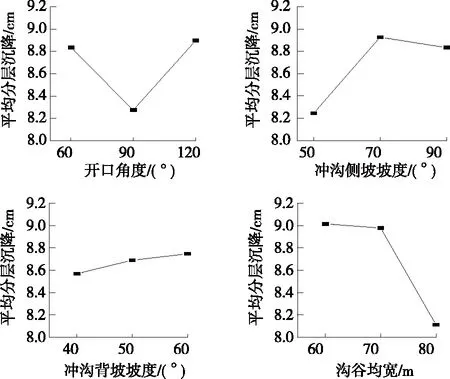
图10 地形因素对平均分层沉降影响的敏感性分析

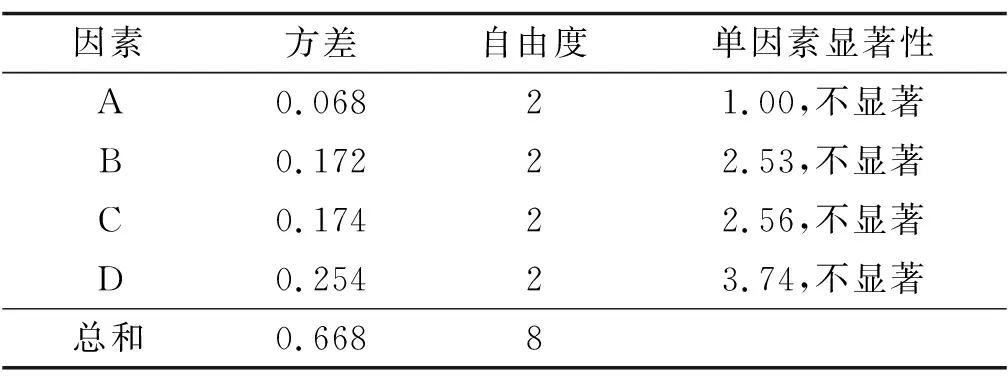
表4 最大分层沉降方差分析

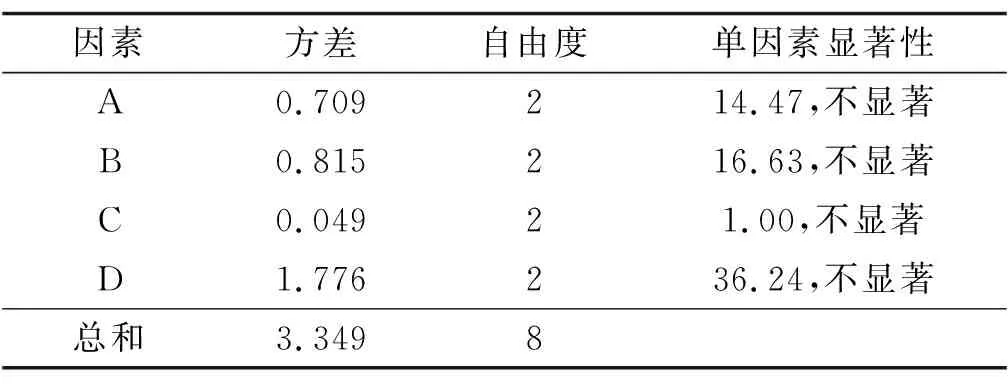
表5 平均分层沉降方差分析

综上，V形冲沟高填路堤分层沉降主要由沟谷均宽引起，且主要影响平均分层沉降，线路规划过程中应选取适宜沟谷均宽的冲沟地形。

2.4 地形因素对分层侧移的影响分析

分层侧移的极差分析见表6，各因素对最大分层侧移和平均分层侧移影响的直观分析见图11、图12。从图11、图12可看出：各地形因素对高填路堤最大分层侧移ηmax影响的敏感性依次为D>B>A≈C，对平均分层侧移¯η影响的敏感性依次为D>B>C>A。

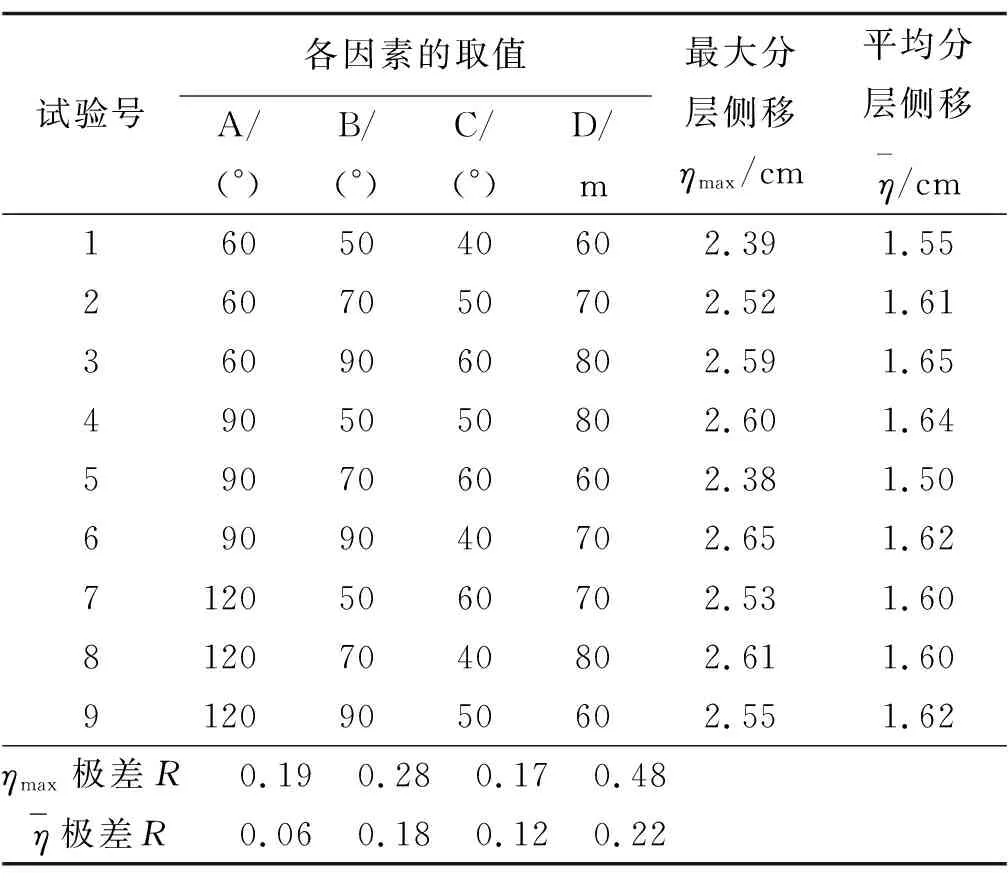
表6 分层侧移极差分析

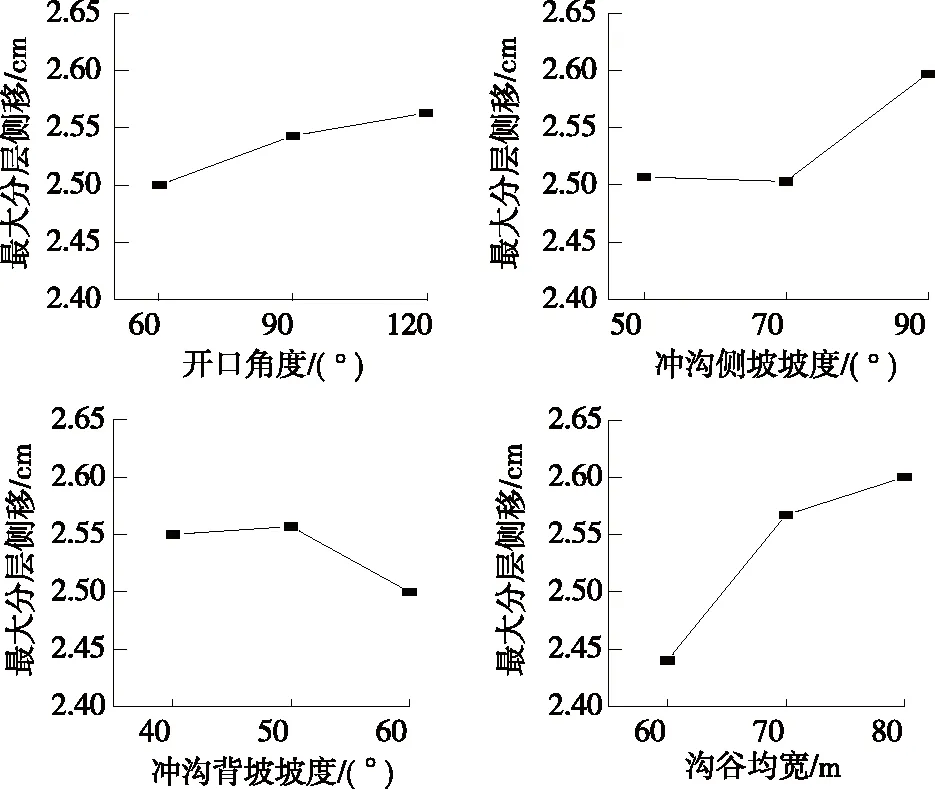
图11 地形因素对最大分层侧移影响的敏感性分析

分层侧移的方差分析见表7、表8。在置信水平α=0.05的条件下，对于最大分侧移，各因素影响均不显著；对于平均分层沉降，因素C、D的影响显著，因素A、B的影响不显著。与极差分析结果一致。

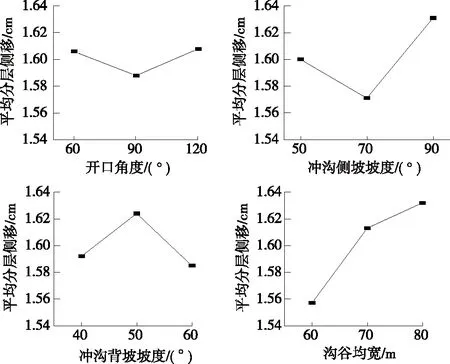
图12 地形因素对平均分层侧移影响的敏感性分析

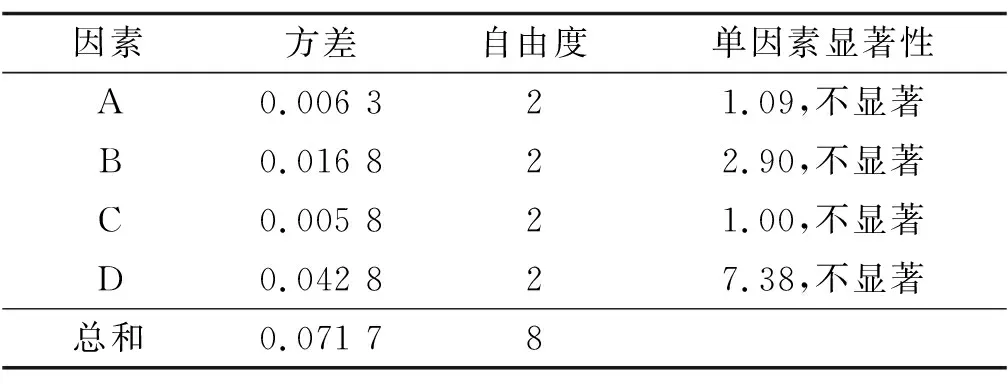
表7 最大分层侧移方差分析

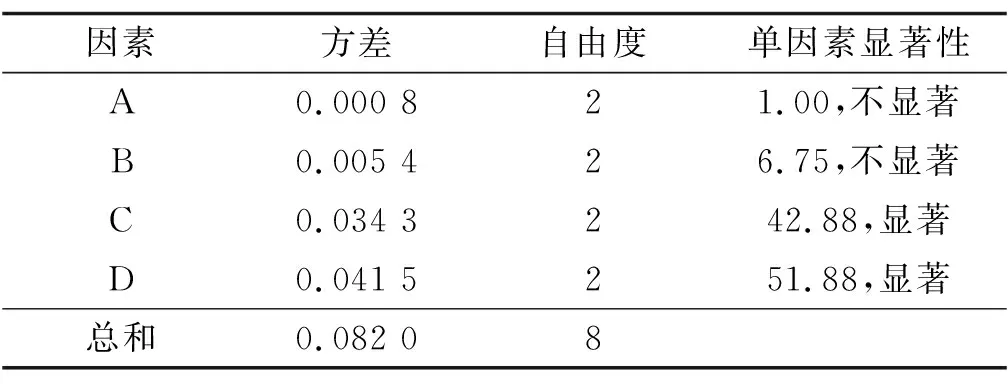
表8 平均分层侧移方差分析

综上，V形冲沟高填路堤分层侧移主要由沟谷均宽和冲沟背坡坡度引起，且主要影响平均分层侧移，线路跨越冲沟地形时应注意选取合适的沟谷均宽和冲沟背坡坡度。

3 结论

依托杭绍台高速公路(台州段)扩建工程，通过正交试验研究V形冲沟地形条件下高填路堤的变形特性，得到以下主要结论：

(1) 无论是在二维还是三维条件下，高填路堤的分层沉降与分层侧移均随施工步(填筑高度)不断增大，沿高程方向均呈现中间大、两头小的发展形态，且二维条件下高填路堤的分层沉降和分层侧移比三维条件下分别大3%～5%和5%～10%。

(2) V形冲沟的三维特性可归纳为开口角度、冲沟侧坡坡度、冲沟背坡坡度和沟谷均宽4个地形因素。对于平均分层沉降，沟谷均宽的影响显著，其余因素不显著；对于平均分层侧移，沟谷均宽和冲沟背坡坡度的影响显著，其余因素不显著。V形冲沟地形条件下修筑高填路堤应重点关注沟谷均宽和冲沟背坡坡度。