动态无功电压控制对频率振荡的影响及附加阻尼控制

李小菊，李青兰，詹航，司萌，陈磊，闵勇

(1. 国网重庆市电力公司电力科学研究院，重庆 401121；2. 清华大学电机工程与应用电子技术系，北京 100084)

0 引言

近年来，频率振荡事件多次出现于实际系统[1 - 4]。国内典型的频率振荡事件为2016年在云南电网异步联网试验中出现了频率低于0.1 Hz的振荡[3 - 4]。国内外展开了大量对频率振荡的研究工作。研究指出，频率振荡属于小扰动频率稳定问题，由电力系统有功频率控制过程中的小扰动不稳定引起。频率振荡表现为系统中所有发电机转速同调变化、系统频率整体振荡。一般振荡频率低于0.1 Hz，也称为超低频振荡[1 - 7]。

由于频率振荡是有功频率控制过程中的小扰动不稳定问题，因此对频率振荡的分析和控制主要集中于有功频率控制环节，尤其是发电机原动系统，抑制频率振荡的方法也是对调速器的参数优化。文献[8 - 12]都针对调速器进行了研究，并提出了相应的调速参数优化方法或附加阻尼控制策略以提高频率振荡阻尼。但是通过调速器抑制频率振荡也有其不足：一方面，因为调速器属于机械部件，在实际应用时会有灵敏度和磨损的问题；另一方面，提高频率振荡的阻尼和机组一次调频响应在进行调速器参数优化时不可同时兼备，若提高频率振荡阻尼，那么可能会恶化一次调频响应。除了调速器上的改进措施外，文献[13]利用储能控制抑制频率振荡，也是在有功频率控制环节进行的工作。

虽然频率振荡是有功频率控制过程的小扰动不稳定问题，但是，电力系统中无功电压控制过程和有功频率控制过程不是解耦的，无功电压控制也可以影响系统有功进而影响频率振荡。可以针对频率振荡为动态无功电压控制设备设计相应的阻尼控制环节提高频率振荡的阻尼。针对系统中已有的动态无功电压控制设备，增加附加控制的成本很低，在调速器参数优化之外提供一种频率振荡抑制的备选辅助手段，而且相比于机械部件的调速器，动态无功电压控制设备为动作灵敏、快速，不存在磨损的问题，可以为抑制频率振荡提供一种新的备选辅助手段。

本文所说的动态无功电压控制设备含义很广，包括专门的动态无功补偿设备如SVC、STATCOM，以及风电、光伏等新能源以及电池储能系统的无功电压控制环节，还有传统同步发电机的PSS等。PSS向励磁提供附加控制信号，改变励磁电压，本质上属于无功电压控制环节，文献[14 - 17]就是利用发电机PSS的改进或参数调整抑制频率振荡，说明无功电压控制确实可以影响频率振荡。但是，这些研究还是局限于PSS，没有从更加基础的层面去分析无功电压控制影响频率振荡的机理。

针对上述问题，本文首先分析了动态无功电压控制设备影响频率振荡的机理，然后提出了抑制频率振荡的附加阻尼控制策略，并分析了不同位置无功电压控制设备对频率振荡的影响大小。本文所提出的方法均在新英格兰10机39节点系统中验证了其正确性和有效性，并在某实际电网中进行了验证。

1 动态无功电压控制对频率振荡的影响分析

对于一个原始的包含无功电压控制设备的多机系统，在忽略网损和负荷仅考虑频率调节效应的情况下，文献[16]推导出图1所示的等值模型准确的计算频率振荡模式。图1的模型中不包含任何无功电压控制环节，说明原始系统中的无功电压环节对频率振荡模式的计算没有影响，即不考虑网损和负荷仅考虑频率调节效应的情况下，动态无功电压控制不会对频率振荡产生影响。

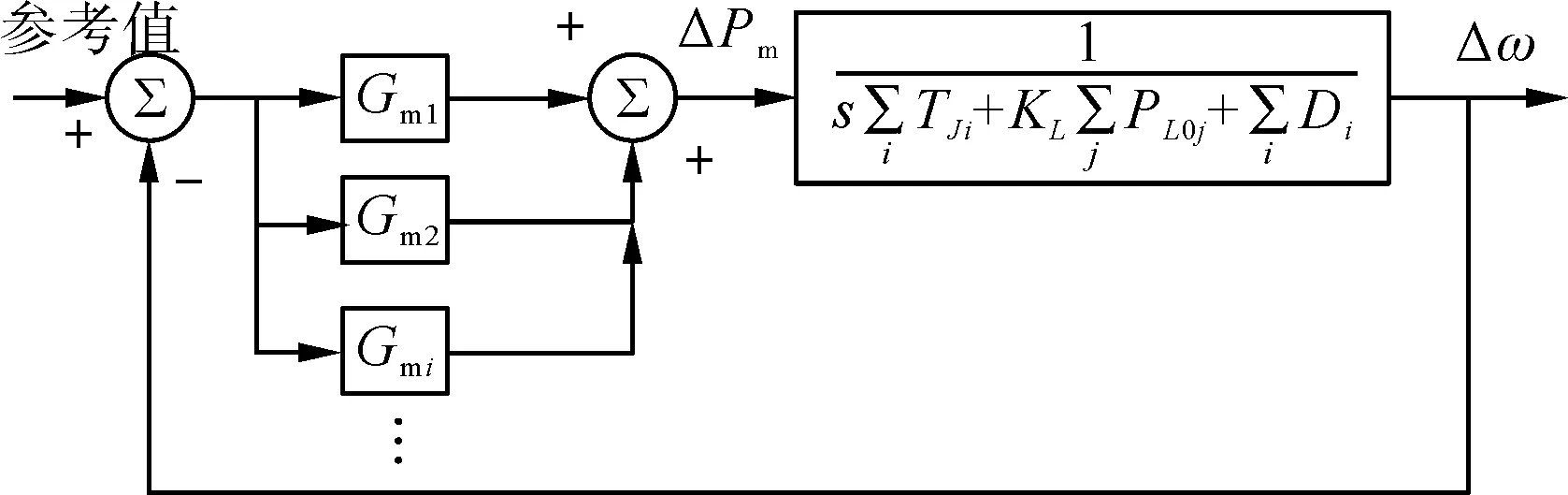
图1 多机系统中计算频率振荡模式的系统框图Fig.1 Block diagram for calculating frequency oscillation mode of multi-machine system

但是，实际电网中负荷具有电压调节效应，此时，无功电压控制会使节点电压发生变化，从而使负荷有功发生变化，无功电压控制和有功频率控制产生耦合，所以无功电压控制就会对频率振荡产生影响。网络电阻的存在也会产生类似影响，但影响大小一般比负荷的电压调节效应小。

因此，负荷的电压调节效应是无功电压控制影响频率振荡的桥梁。负荷具有电压调节效应，无功电压控制就会影响频率振荡。下面进行更加具体的分析。考虑式(1)所示的静态负荷模型。

(1)

式中：PL为负荷有功功率；PL0和U0分别为有功负荷和节点电压的额定值；U为负荷节点电压；Δf为频率偏差；KL为负荷频率调节效应系数；KZ和1-KZ分别是恒阻抗、恒功率负荷的比例系数。

对式(1)的负荷模型进行线性化处理，可得：

(2)

由于频率振荡中所有发电机转速同调，将所有发电机等值为1台机，线性化后的转子运动方程为：

(3)

式中：TJi、Di分别为发电机i的转子惯性时间常数和阻尼系数；Δω为发电机转速偏差；ΔPm、 ΔPe为所有发电机机械功率偏差、电磁功率偏差之和，忽略网损则ΔPe=ΔPL=KfΔf+KUΔU。

修改图1的模型使其包含KUΔU的影响，如图2所示。如果KZ=0，负荷没有电压调节效应，KU=0，无功电压控制不影响频率振荡；如果KZ≠0，负荷具有电压调节效应，KU≠0，无功电压控制就会通过图2中以ΔU作为输入的环节影响频率振荡。

图2 考虑负荷电压调节效应的频率振荡模式计算模型Fig.2 Diagram for frequency oscillation calculation mode considering voltage regulation effect of load

2 动态无功电压控制通过附加控制产生的频率振荡阻尼转矩

2.1 产生阻尼转矩的原理和过程

文献[6]将阻尼转矩法应用于频率振荡的阻尼分析。在频率振荡中，电磁功率偏差与发电机转速偏差(或系统频率偏差，频率振荡时两者相同)同相位的分量为正的阻尼转矩分量。对于给定系统，可以得到电磁功率偏差ΔPe与转速偏差Δω之间的传递函数为Ge(s)=ΔPe/Δω， 设振荡频率为ωd， 将s=jωd代入可得：

Ge(jωd)=KD+jKS

(4)

式中：KD=Re(Ge(jωd))为电磁功率的阻尼转矩系数；KS=Im(Ge(jωd))为电磁功率的同步转矩系数。若KD为正数，则有利于振荡的衰减。

因此，可以对动态无功电压控制设备设计以系统频率偏差Δf为输入信号的附加控制环节，通过附加控制环节产生ΔPe与Δf同相位的分量，增大电磁功率阻尼转矩系数KD， 从而提振荡阻尼。简单的附加控制可以考虑增加以Δf为输入的比例环节。

负荷电压调节效应是无功电压控制过程与有功频率控制过程耦合的纽带，无功电压控制使得电压变化，导致负荷有功变化。具体过程如图3所示。其中，GSC(s)是附加控制的传递函数，输入为Δf， 输出为附加控制信号USCS；GQ(s)表示的是无功电压控制设备输入信号到输出无功功率ΔQ的传递函数；输出无功ΔQ影响负荷节点电压ΔUL， 之间的系数KQU为与网络相关的系数；ΔPL为负荷有功功率，KU反映负荷电压调节效应系数。一般情况下，系数KQU和KU为正实数，只要使得Re(GSC(jωd)GQ(jωd))>0， 就可增大ΔPL中与Δf同相位的分量，即增大阻尼转矩分量，从而提高频率振荡的阻尼。

图3 动态无功电压控制影响有功功率偏差示意图Fig.3 Diagram of dynamic reactive power-voltage control affecting active power deviation

因此，动态无功电压控制设备的阻尼特性受到GSC(s)GQ(s)特性尤其是相位特性的很大影响。为抑制频率振荡，附加控制GSC(s)应该在超低频段尽量补偿GQ(s)的相位滞后。在发电机的励磁控制中，PSS以Δf作为输入，就是图5中的GSC(s)， 然后通过励磁系统和发电机环节(即GQ(s))产生无功输出ΔQ， 如果PSS能够补偿励磁系统和发电机环节产生的相位滞后，就可以对频率振荡产生正阻尼，这是文献[14 - 17]中抑制频率振荡的PSS设计或整定的基本原理。采用电力电子接口的动态无功补偿设备响应速度很快，时间常数远小于频率振荡的周期，一般情况下，在超低频段GQ(s)的相位滞后很小。本文以STATCOM为例，采用PSD-BPA中的模型，如图4所示。

图4 STATCOM模型Fig.4 STATCOM model

图4中U为STATCOM节点电压；UREF为STATCOM节点参考电压；USCS为附加信号；T1为滤波器和测量回路的时间常数；T2、T3、T4、T5分别为各级的超前或滞后时间常数；TP为比例环节时间常数；KP为比例环节放大倍数；KI为积分环节的放大倍数；TS为STATCOM响应延迟；KD为STATCOM的U-I特性曲线的斜率；UMAX为电压限幅环节的上限；UMIN为电压限幅环节的下限；ICMAX为最大容性电流；ILMAX为最大感性电流。本文对此模型进行简化，不考虑两个超前滞后环节，即(1+sT2)/(1+sT3)=1， (1+sT4)/(1+sT5)=1， 此时有：

(5)

采用参数：T1=0.02，KP=10，TP=0.02，KI=50，KD=0.03，TS=0.02， 0～2.5 Hz频段的相频特性如图5所示，相位滞后在10 °以内。此时附加阻尼控制器GSC(s)的设计非常简单，采用比例控制即可，整个GSC(s)GQ(s)的相位滞后很小，动态无功电压控制环节产生正的阻尼转矩。但是，具体的相位滞后大小和参数有关，如果某些参数下相位滞后较大，在设计GSC(s)是需要考虑一定的相位补偿，此时可以参考PSS的相位补偿方法。

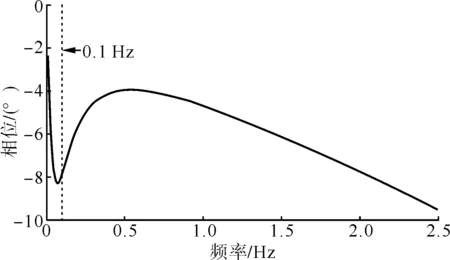
图5 动态无功补偿设备的相频特性Fig.5 Phase-frequency characteristics of STATCOM

在图4基础上，增加以Δf为输入信号的附加信号，即USCS=KSΔf， 形成如图3所示的Δf与ΔPL之间的关系。若KS>0，则Re(GSC(jωd)GQ(jωd))>0， 通过增加USCS=KSΔf环节可增加系统电磁功率的阻尼转矩系数，从而提高系统的频率振荡阻尼。

在图6所示的新英格兰10机39节点系统进行仿真分析。详细的网络参数和结构介绍见文献[18]，忽略网损，即支路电阻都设为0。发电机采用四阶模型，发电机励磁系统和发电机原动机均采用与文献[5]相同的模型和参数。负荷模型为式(1)，其中KL=1、KZ=0.4。分别在节点7、节点15和节点26处增加STATCOM，附加信号USCS=KSΔf。 同时改变3个STATCOM的参数KS， 计算系统频率振荡的特征值，得到频率振荡模式阻尼比随KS变化的曲线如图7所示。由仿真结果可知，随着KS的增加，系统频率振荡的阻尼比随之提高。考虑到控制一般具有两面性，增大KS提高频率振荡模式阻尼时，可能影响电压控制效果或低频振荡模式的阻尼，综合本文STATCOM模型参数与控制效果，本文仿真中KS参数范围为[0,30]。后续还需要进一步研究兼顾不同控制目标的协调控制算法[20]。

图6 带有STATCOM的新英格兰10机39节点系统Fig.6 New England 10-machine 39-bus system with STATCOMs

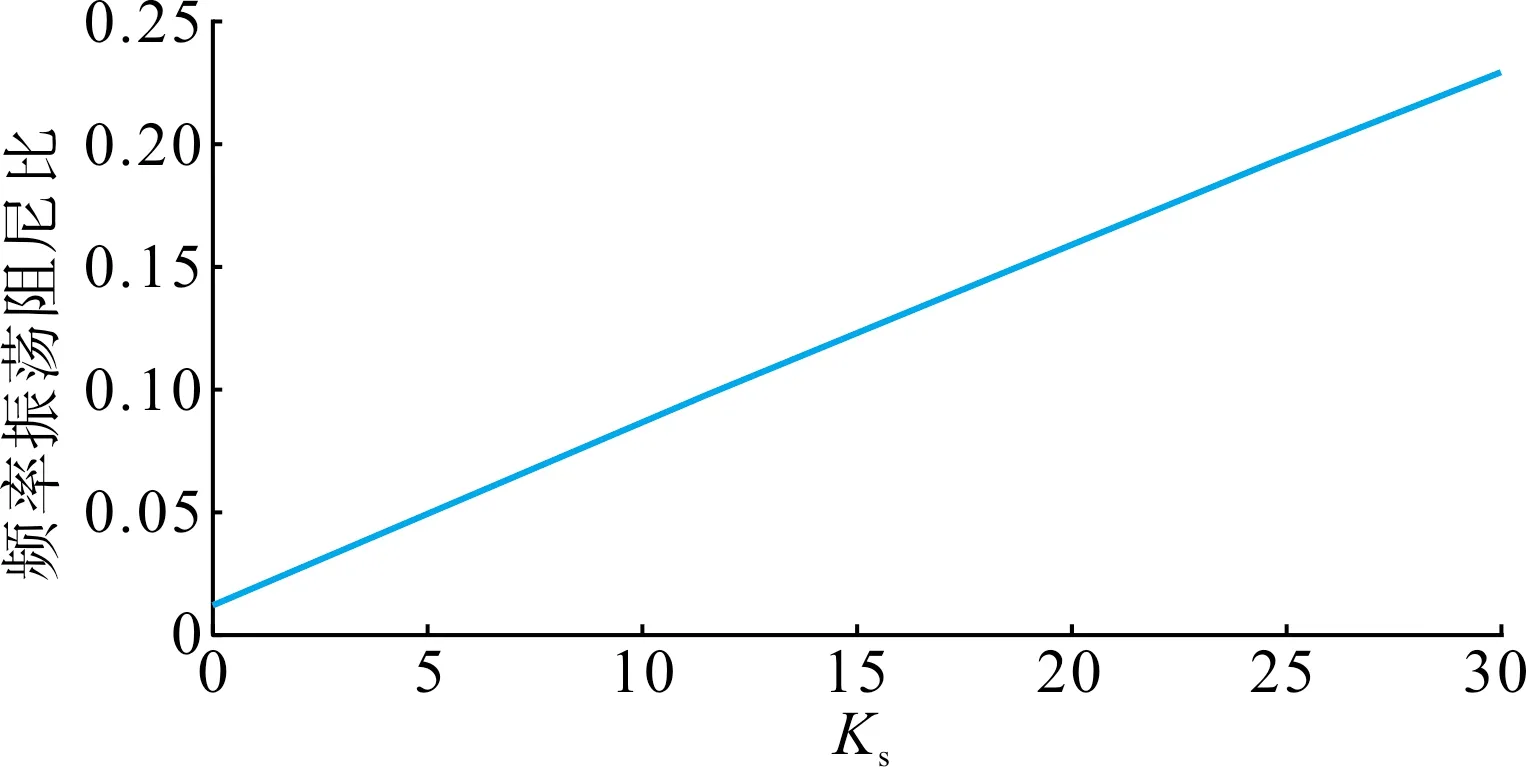
图7 频率振荡阻尼比随KS变化曲线Fig.7 Curve of frequency oscillation damping ratio changing with Ks

分别在KS=0、KS=15和KS=30的情况下进行时域仿真，对发电机转速偏差施加一个小的初始扰动，得到发电机G1转速偏差曲线如图8所示。

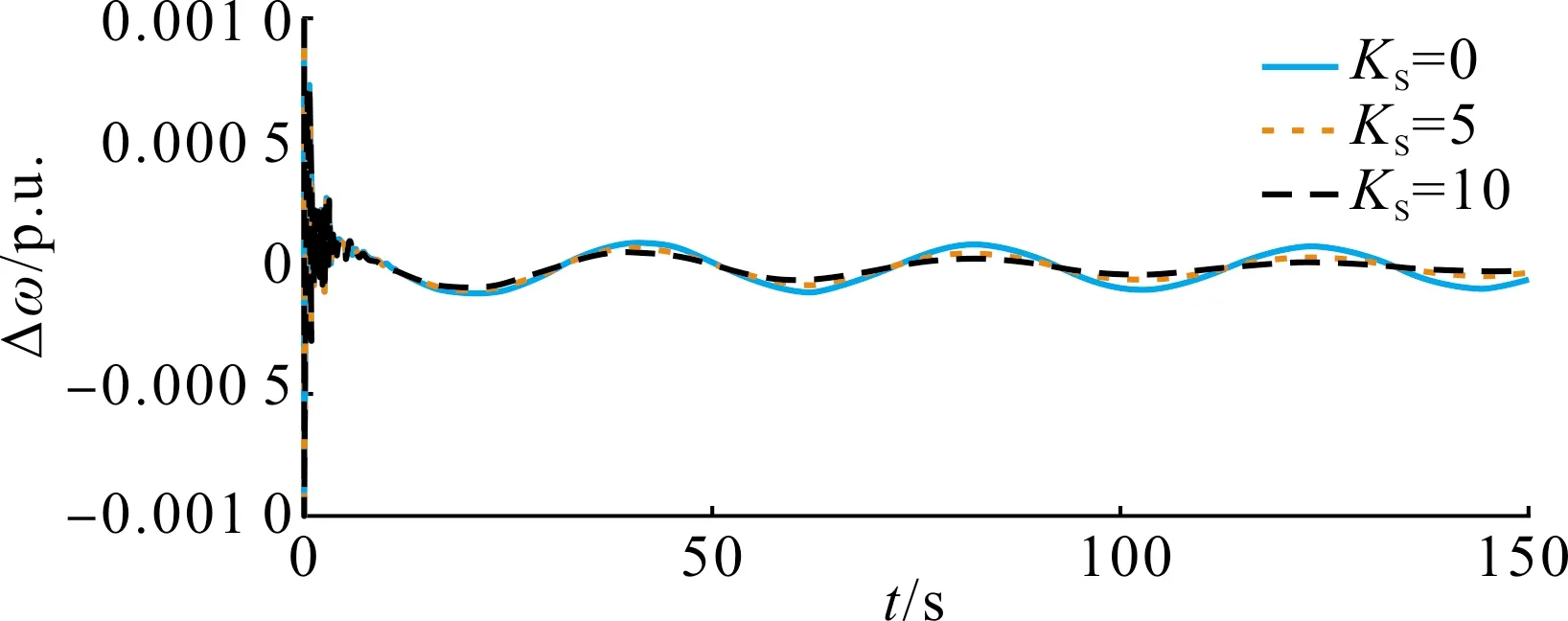
图8 不同KS下G1转速偏差时域仿真曲线Fig.8 Time domain simulation curves of G1 speed deviation with different Ks

由图8可知，曲线的前几秒为低频功角振荡模式的体现，低频振荡平息后主要体现为频率振荡模式。由时域仿真结果可知，KS越大，系统频率振荡越容易衰减。因此，本节所提出的阻尼控制策略能有效增加系统频率振荡的阻尼比，可以为提供频率振荡的阻尼提供一种新的辅助手段。

2.2 不同位置无功电压控制设备的影响大小评估

(6)

可以通过KSLi评估不同节点的无功电压控制设备对频率振荡的影响大小。KSLi越大，说明该节点无功功率变化对频率振荡的影响越大，在该节点的动态无功电压控制设备上增加阻尼控制能更有效的提高频率振荡模式的阻尼。

在图6所示的仿真系统中进行验证。采用上述方法计算KSLi， 节点输入无功功率变化量ΔQi=0.01，结算节点7、节点15和节点26的KSLi分别为：0.153 4、0.171 1、0.140 8。可知在此系统中，不同节点无功功率变化对频率振荡模式的影响大小为KSL15>KSL7>KSL26。

分别改变接入节点7、节点15和节点26的STATCOM参数KS大小，计算系统频率振荡的特征值，得到频率振荡模式阻尼比随KS变化的曲线如图9所示。结果表明，接入不同位置的STATCOM对频率振荡阻尼的影响大小排序为节点15>节点7>节点26，与KSLi顺序完全一致。可看出频率振荡阻尼比与KS近似成线性关系，计算其斜率分别0.693 1、0.816 1、0.657 0，比例关系为1.000 0:1.177 5:0.948 0，与KSL7:KSL15:KSL26=1.000 0:1.115 5:0.917 9大致相同。

图9 频率振荡阻尼比随不同位置STATCOM参数KS 变化的曲线Fig.9 Curves of frequency oscillation damping ratio changing with Ks of STATCOM at different positions

2.3 讨论

本节提出的附加控制策略，实际上是增大了负荷的频率调节效应系数，在负荷自身的频率调节效应之外，又通过附加控制和负荷的电压调节效应产生额外的频率调节效应，可等价为增大了式(2)的系数KL， 从而提高频率振荡模式的阻尼比。

需要说明的是，动态无功电压控制设备附加控制的效果取决于负荷电压调节效应，只要负荷的电压调节效应为正，附加控制就可以提高频率振荡的阻尼，但负荷电压调节效应的准确大小实际系统中难以获取，因此本节提出的阻尼控制策略主要作为一种辅助手段，在不影响设备主要功能的情况下为频率振荡抑制提供帮助。本文的分析和仿真虽然都是以动态无功补偿设备为例进行的，但结论和方法对于风电、光伏等新能源以及电池储能系统的无功电压控制环节也都是适用的。

3 实际系统仿真分析

本节利用某实际电网BPA数据分析动态无功电压控制设备附加控制对频率振荡的影响。该电网为一个省级电网，总节点数7 778，其中发电机节点数1 320，总发电功率54 995.5 MW，其中70%是水电，用电负荷23 254.7 MW，通过直流外送功率30 007.3 MW。

以STATCOM为例进行仿真分析，BPA数据中的STATCOM模型如图4所示。附加信号USCS控制结构如图10所示。KS1为第一级测量回路增益，KS2为第二级测量回路增益，KS3为增益，TS7为第一级输入滤波器的滞后时间常数，TS10为第二级输入滤波器的滞后时间常数，TS8为第一级超前时间常数，TS9为第一级滞后时间常数，TS11为第二级超前时间常数，TS12为第二级滞后时间常数，TS13和TS15为超前时间常数，TS14和TS16为滞后时间常数，A′为超前识别码，B′为滞后识别码，USCSMAX为信号限幅。

图10 STATCOM附加信号控制模型Fig.10 STATCOM supplementary signal control model

仿真分析中采用静态负荷模型，如式(7)所示，对应于BPA暂态稳定程序中的LB卡。

(7)

式中：U为母线电压；U0为母线电压额定值；Δf为母线频率偏差；P0为有功负荷的额定值；P1为恒定阻抗有功负荷比例；P2为恒定电流有功负荷比例；P3为恒定功率有功负荷比例；LDP为频率变化1%引起的有功变化百分数；Q0为无功负荷的额定值；Q1为恒定阻抗无功负荷比例；Q2为恒定电流无功负荷比例；Q3为恒定功率无功负荷比例；LDQ为频率变化1%引起的无功变化百分数。仿真中数据为：P1=1，Q1=1，LDP=1.2，LDQ=1.2，P2=P3=Q2=Q3=0。

在原BPA数据中，电网中不存在STATCOM，为验证在大电网中动态无功补偿附加控制对频率振荡的影响，分别在母线MJ50、HP50、DLE50、QD50、HH50、LH50接入STATCOM，额定容量为300 Mvar，参数如下：T1=0.02，T2=T3=T4=T5=1，TP=0.02，TS=0.02，KP=10，KI=50，KD=0.03，VMAX=-VMIN=1.0，ICMAX=1.0，ILMAX=1.0。

增加以Δf为输入附加信号USCS， 控制框图如图9所示，参数如下：KS1=10，KS2=0，KS3=30，TS7=0.02，TS8=1.0，TS9=0.02，TS13=1，TS15=1.0，TS14=0.02，TS16=1.0，A′=1，B′=1，VSCSMAX=10。

在BPA暂态稳定程序中进行时域仿真，施加一个功率扰动，得到各发电机时域仿真曲线。STATCOM无附加控制和增加附加控制后发电机XIAOW1G转速偏差时域仿真曲线如图11所示。由图11可知，在增加STATCOM附加控制后，系统频率振荡衰减速度更快，说明增加以Δf为输入的附加控制环节有利于抑制系统频率振荡。

图11 无附加控制和增加附加控制后XIAOW1G机组转速 偏差时域仿真曲线Fig.11 XIAOW1G generator speed deviation time-domain simulation curves without additional control and with additional control

4 结论

近年来，频率振荡问题引起广泛关注，传统控制手段集中于有功功率控制环节，本文提供了一种新的思路，通过动态无功电压控制环节的附加控制提高频率振荡阻尼。通过负荷的电压调节效应，动态无功电压控制设备也可以对频率振荡产生影响，为频率振荡的抑制提供一种辅助的手段。本文首先分析了动态无功电压控制设备通过附加控制产生频率振荡阻尼转矩的原理和过程，然后提出了附加阻尼控制策略。对于采用电力电子接口的快速无功控制设备，在原有无功电压控制环节中增加一个以系统频率偏差为输入的比例环节，即可提高频率振荡模式的阻尼比。同时提出了不同位置设备对频率振荡模式影响大小的评估方法，选择影响大的无功电压控制设备进行阻尼控制可更加有效的提高频率振荡阻尼。

需要强调的是，本文提出的控制策略主要作为一种备选的辅助手段，无法完全取代有功功率控制环节各种控制措施的作用。动态无功电压控制设备的附加阻尼控制效果取决于负荷电压调节效应，只要负荷的电压调节效应为正，附加控制就可以提高频率振荡的阻尼，但负荷电压调节效应的准确大小实际系统中难以获取，因此本文提出的控制策略效果难以准确评估，主要作为一种辅助手段。如果电网中已有一些动态无功补偿设备，在不影响设备主要功能的情况下为频率振荡抑制提供帮助，成本较低，可以作为一种备选的辅助手段。