基于小波包样本熵和支持向量机的框架结构损伤识别
2021-07-29方有亮李肖磊王晶晶
方有亮,李肖磊,张 颖*,王晶晶,刘 乐
(1.河北大学建筑工程学院,保定 071000;2.河北省土木工程监测与评估技术创新中心,保定 071000)
近年来,结构损伤检测技术一直是国际学术界和工程界研究的热点。基于振动测试的损伤识别方法取得了飞快的发展[1-2],很多机器学习的算法被应用到该领域,主要有神经网络[3]、小波分析[4]、遗传算法[5]、支持向量机等。Kourehli[6]提出一种利用静态响应和支持向量机进行结构损伤检测和估计的方法,分析得知即使存在不完全噪声数据和建模误差,该方法对结构的损伤定位和严重程度依然很敏感。刘泽佳等[7]结合了结构响应向量与支持向量机的损伤识别方法,在简支梁和实际桥梁模型中都验证了方法的有效性。张颖等[8]以钢框架模型的试验模态频率作为支持向量机的训练和测试样本的输入,支持向量机输出判断损伤位置,研究表明该算法对损伤位置敏感、识别精度较高。
熵对系统的非线性特征具有显著的凸显作用,其常见度量方法有近似熵和样本熵等。样本熵是一种用来描述时间序列复杂度的新方法,对所需的数据长度要求不高、抗噪声干扰能力强。孙增寿等[9]在小波包分析过程中结合样本熵建立了对数加速度能量差小波包样本熵作为损伤指标,识别效果显著且具有良好的鲁棒性。孙柯等[10]提出了小波包频带内局部样本熵的概念,将测点的时程数据进行小波包分解与重构,计算局部时间区间的样本熵作为损伤指标,通过有限元模型分析验证了方法的可行性。近年来样本熵被广泛应用于机械故障诊断[11]和医学信号处理[12]等领域。
现提出采用样本熵特征向量和支持向量机(support vector machine,SVM)相结合的方法,对四层钢框架结构进行损伤识别。利用单个加速度振动响应信号,进行小波包分解,提取样本熵作为特征值向量,该方法能有效地识别结构损伤位置和程度。
1 基本理论
1.1 小波包分析
小波分析只分解信号的低频部分(S),而对信号的高频部分(d)不再分解,导致信号的细节部分没有被分析,小波变换能很好地表征一大类以低频信息为主要成分的信号,但不能分解和表示包含大量细节信息的信号,比如非平稳的机械振动信号等。相比小波分析,小波包分析在信号处理方面作了进一步精细化,不仅信号的高频部分分辨率优于小波分析,还可以自适应地选择最佳的小波基函数。既无冗余,也无疏漏,对于信号能够更好地时频局部化分析。小波包3层分解结构如图1所示,Layer 0代表原始信号,经过小波包分解得到Layer 1的低频(S)和高频(d)两个节点信号,然后分别对低频(S)和高频(d)信号再进行一次小波包分解,得到Layer 2的4个节点信号,以此类推,经过3层分解后得到Layer 3的8个节点信号。
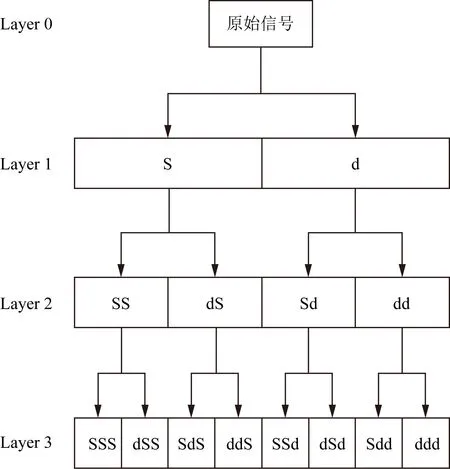
图1 小波包3层分解结构图Fig.1 Wavelet packet 3-layer decomposition structure diagram
对于一个在时域上采集的信号函数f(t),经过j层小波包分解后可以用式(1)表示:
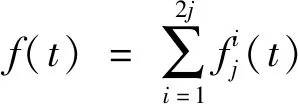
(1)
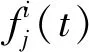

(2)
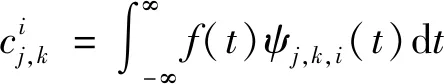
(3)
式(3)中:ψj,k,i(t)是具有尺度指标j、位置指标k和频率指标i的小波包函数。
1.2 样本熵
假设由小波包分解的各阶分解信号{x(n)}={x(1),x(2),…,x(N)}的数据个数为N个,则其样本熵计算步骤如下。
(1)由N个数据组成的时间序列{x(n)}={x(1),x(2),…,x(N)},按序号组成一组维数为m的向量序列,Xm(1),Xm(2),…,Xm(N-m+1),其中Xm(i)={x(i),x(i+1),…,x(i+m-1)},1≤i≤N-m+1。这些向量代表从第i点开始的m个连续的x的值。
(2)定义向量Xm(i)与Xm(j)之间的距离d[Xm(i),Xm(j)]为两者对应元素中最大差值的绝对值。即
d[Xm(i),Xm(j)]=maxk=0,1,…,m-1(|x(i+k)-
x(j+k)|)
(4)
(3)对于给定的Xm(i),统计Xm(i)与Xm(j)之间距离小于等于r的j(1≤j≤N-m,j≠i)的数目,并记作Bi。对于1≤i≤N-m,定义
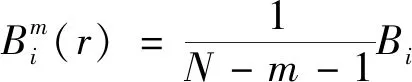
(5)
(4)定义B(m)(r)为
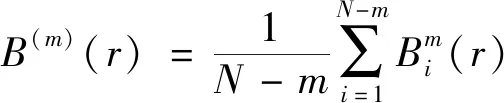
(6)
式(6)中:Bm(r)为两个序列在相似容限r下匹配m个点的概率。
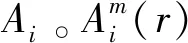
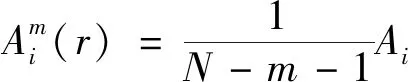
(7)
(6)定义Am(r)为
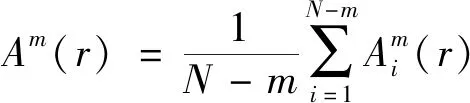
(8)
式(8)中:Am(r)为两个序列匹配m+1个点的概率。
样本熵定义为
(9)
当N为有限值时,可以用式(10)估计:
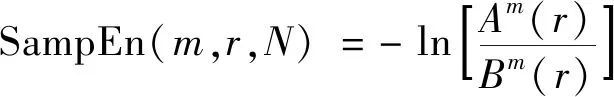
(10)
式(10)中:m为初始分段,每段的数据长度,重构维数,一般选择1或2,一般不取m>2,这里取m=1;r为阈值,一般选择r=(0.1~0.25)Std(data),其中Std(data)表示数据data的标准差。现采用r=0.15Std(data)。
1.3 SVM
支持向量机[13](support vector machine,SVM)是由苏联教授Vapnik等于1995年提出的,基于VC维理论和统计学习理论的结构,根据风险最低的原则,可以使用有限样本提供的信息来找到模型的复杂性与学习获得最佳泛化能力之间的最佳折中。
对于线性可分离性,支持向量机的分类算法从最佳分类面扩展而来的,原空间不可分的样本通过核函数映射到一个高维空间,从而可以在新的线性可分离空间内线性分离或者近似线性分离,在此空间中创建具有最大分类间隙的线性分类超平面,以对数据进行分类识别。如图2所示,图中圆圈和三角形分别代表两类不同的训练样本C1、C2。两条实线代表把两类样本正确分开的分类面,包括超平面P1以及最优超平面P0。两条虚线是每种类型样本最靠近超平面的点,且平行于最佳超平面P0。虚线之间的距离称为分类间隙D,沿虚线通过的点称为支持向量。最佳超平面不仅可以正确区分样本,而且可以最大程度地提高分类间隙D。较大的分类间隙实际上保证了最低的风险。

图2 支持向量机SVM示意图Fig.2 Support vector machine schematic
给定样本集{xi,yi|i=1,2,…,m},其中xi∈Rn表示输入矢量样本,yi∈{-1,1} 表示对应的类别符号,m为样本数,分类面方程wx+b=0 满足:
yi(wxi+b)-1≥0;i=1,2,…,l
(11)
式(11)中:w为样本的参数矩阵;b为类阈值。这样分类间隔D=2/‖w‖,因此使得D最大,等价于‖w‖最小,满足式(11)使‖w‖最小的分类面就是最优分类面,将上述问题表示为
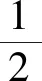
i=1,2,…,l
(12)
定义拉格朗日函数:

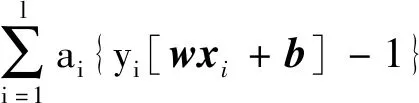
(13)
式(13)中:ai≥0为拉格朗日乘子,可以将上述问题转化为对偶问题:
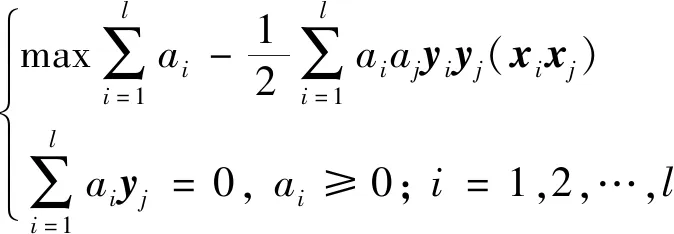
(14)
式(14)是一个二次规划问题,存在唯一解,且解中只有少部分ai不为零,其对应的样本就是支持向量。最终得到的最优分类函数为
(15)
式(15)中:n<l是支持向量个数;xi是支持向量;ai是对应的拉格朗日乘子;b是分类阈值,可用两类中任意一对支持向量取中值求得。
2 数值仿真分析
2.1 损伤定位识别分析
以一个4层的平面钢框架结构为例,每层高度280 mm,跨度280 mm,框架结构的梁和柱为长280 mm、宽30 mm、厚8 mm的钢板条,梁、柱之间连接的结点假设为刚结点。材料弹性模量E=2.1×105N/mm2,泊松比ν=0.3,密度ρ=7.85×10-6kg/mm3。钢架结构模型简图如图3所示,结构测点和单元编号如图4所示。
假设钢框架结构发生损伤,对其进行损伤位置识别。结构的损伤假设不改变损伤单元的质量,只改变损伤单元的刚度,通过刚度折减系数k来表示损伤程度,k取0~1。当k=0时,表示结构为完好状态;当k=1时,表示结构为完全损伤状态。本节采用的刚度折减系数为0.2,分为单损伤和多损伤两种工况进行分析验证,具体的损伤工况如表1所示。
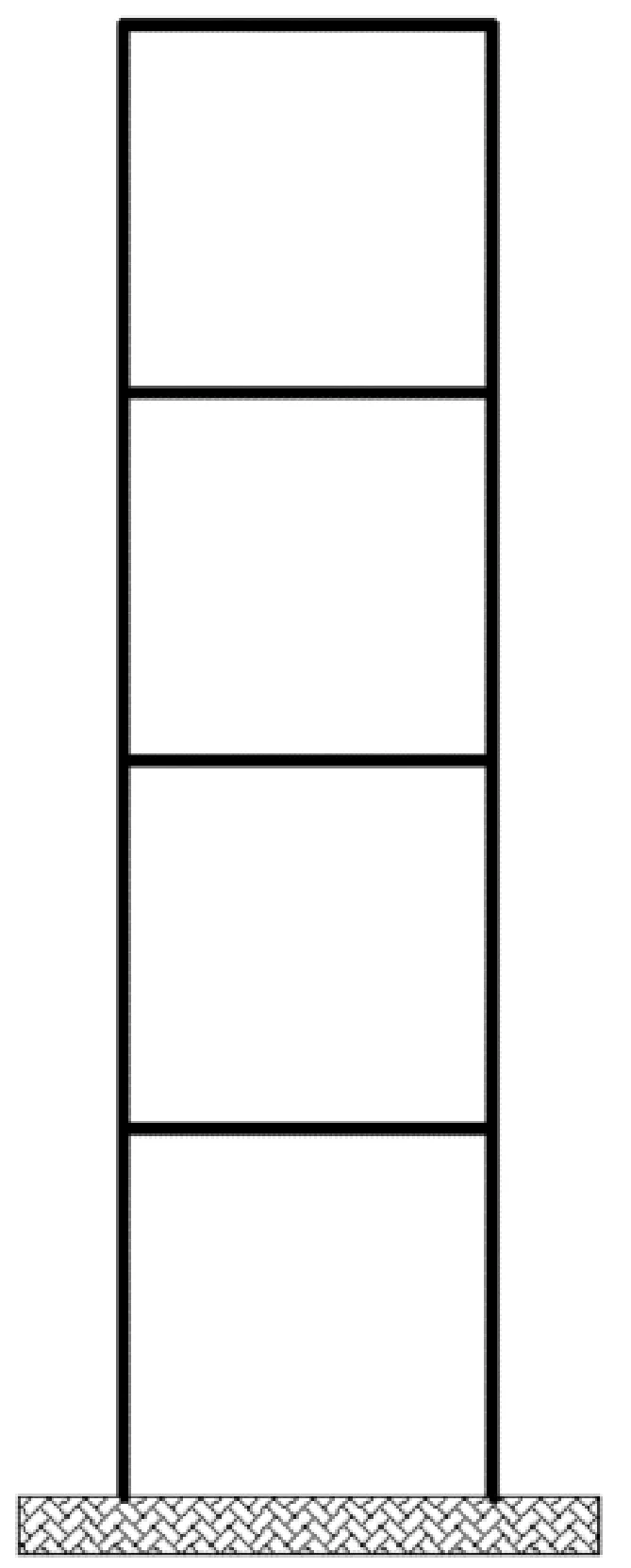
图3 钢框架结构模型及简图Fig.3 Steel frame structure model and diagram

1~10代表结构测点编号;①~代表单元编号图4 结构测点和单元编号Fig.4 Structural points and element numbers
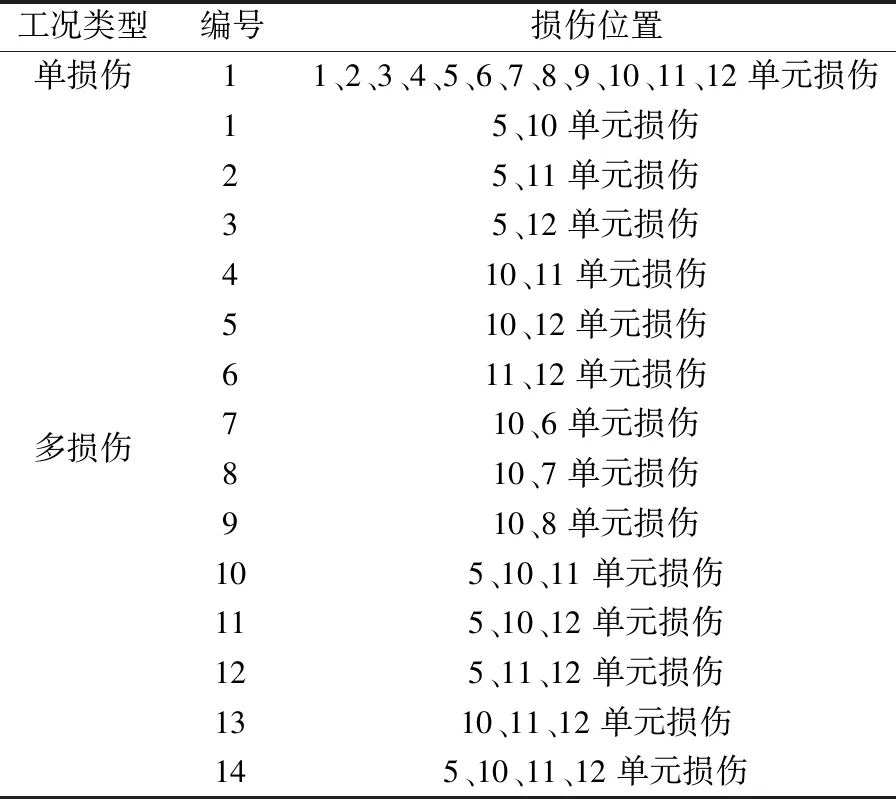
表1 损伤工况Table 1 Damage condition
在MATLAB中对四层钢框架结构进行动力响应有限元分析,在2号测点施加冲击荷载,力的大小范围240~270 N,共施加16次不同的冲击荷载,在6号测点采集加速度响应,采样频率为1 000 Hz。冲击荷载240 N的时程图如图5 所示。
如图6所示,给出第10单元损伤情况下,测点6的加速度相应信号及小波包分解过程。采用Daubechies(db5)小波函数进行3层分解,得到第3层的分解信号共8个节点,对每一个节点的信号计算样本熵,得到如表2所示的样本熵特征值,选择显示前0.2 s的响应信号。
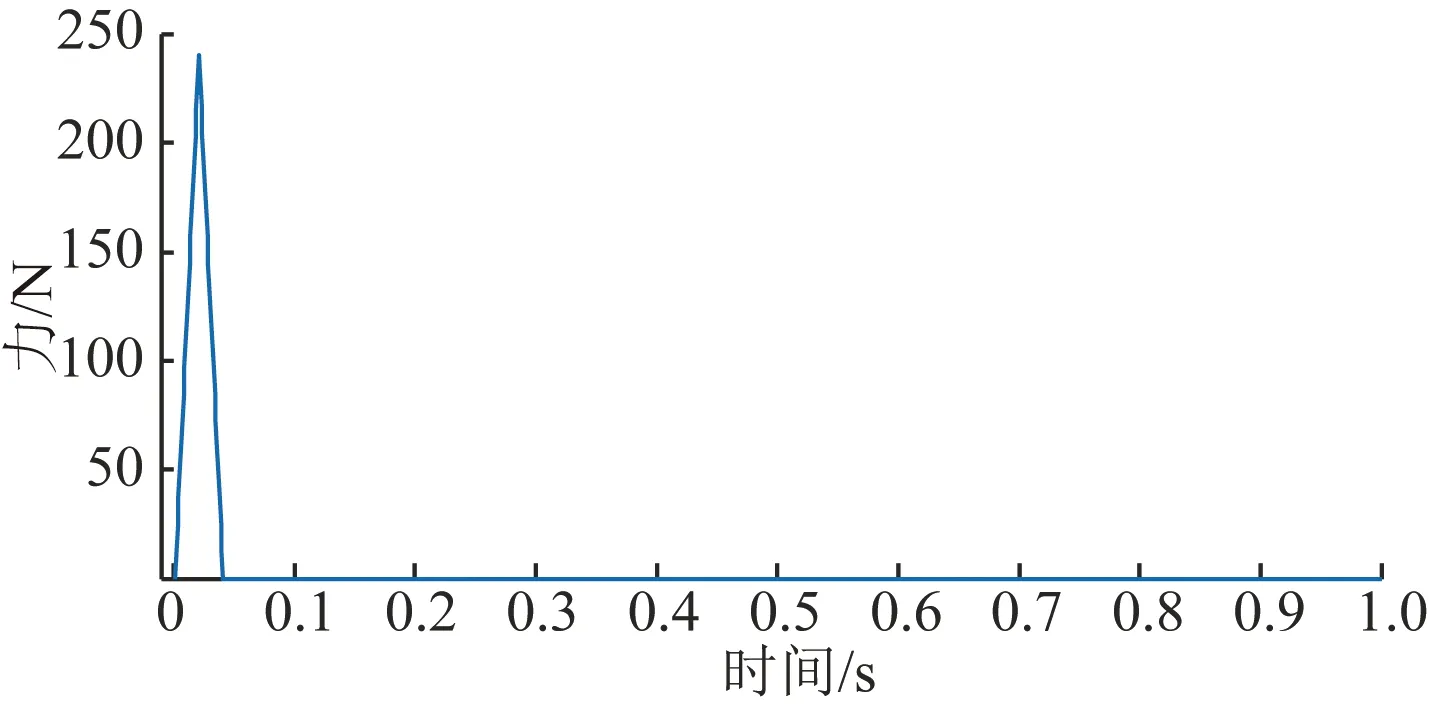
图5 冲击荷载Fig.5 Impact load
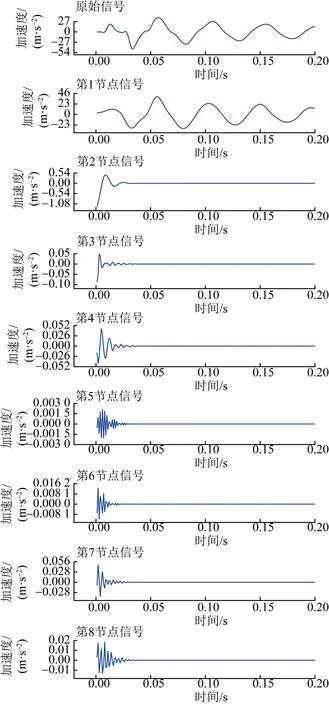
图6 小波包分解信号Fig.6 Wavelet packet decomposition signal
如表1所示的损伤工况,对每一种损伤工况下,施加不同冲击荷载,得到16组加速度响应,对每一组进行小波包3层分解,计算每一节点信号的样本熵特征向量,作为SVM机器学习的数据样本集。随机抽取10组样本熵特征向量,作为支持向量机的训练集,构建SVM模型,其他6组作为支持向量机的测试集,预测结构损伤情况。识别结果如图7所示。
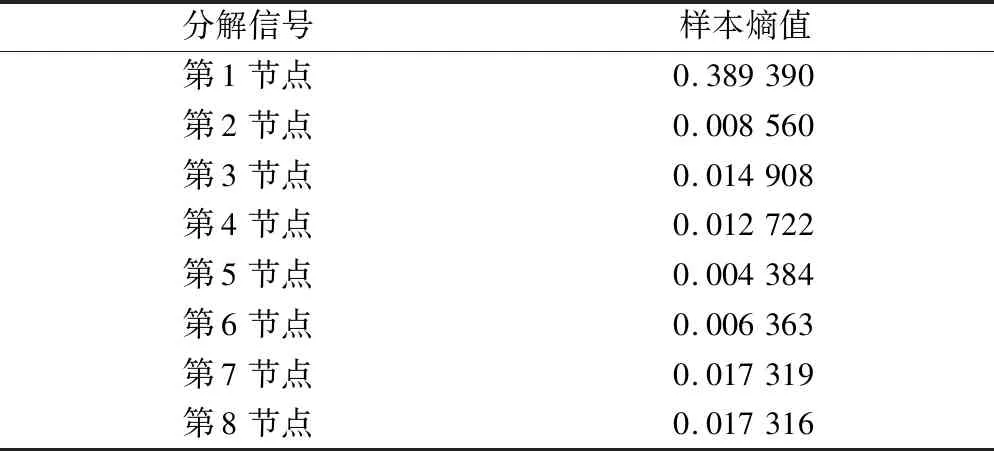
表2 样本熵值Table 2 The sample entropy
如图7所示,横坐标表示测试集的数据编号,每组有6个样本熵值,代表一种损伤工况;纵坐标则表示对应的损伤工况标签。圆圈符号与星号分别代表损伤的实际工况与预测工况,当两者重叠,说明识别准确。SVM的分析结果可见,当钢框架结构发生单一损伤、多损伤时,识别正确率都能达到100%。基于样本熵和SVM的定位识别达到了较好的效果。
2.2 损伤程度分析
确定了损伤位置后,需要对其损伤程度作进一步的评估。本节假设损伤工况为第10单元损伤,对不同的损伤程度进行分析,损伤程度k取0.1、0.2、0.3、0.4、0.5。如图8所示,随着损伤程度的增大,其加速度响应的幅值逐渐减小,而且信号的周期会随之增大,即频率减小。如图9所示,纵坐标为五种损伤程度,横坐标为测试集编号,可见识别结果精确度为100%。
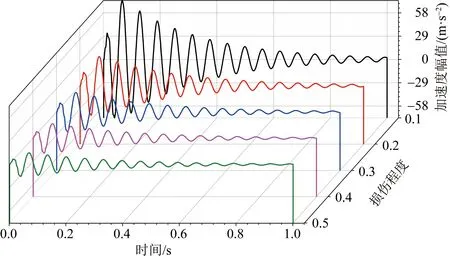
图8 不同损伤程度采集的加速度信号Fig.8 Acceleration signals collected at different damage degrees

图9 不同损伤程度的识别结果Fig.9 Identification results of different damage degrees
2.3 鲁棒性分析
为模拟实测时噪声的影响,需要对数值模拟得到的加速度、速度、应变、位移等结构响应或者动力响应中加入不同程度的噪声[14]。测试噪声主要由环境激励、传感器本身和测量仪器产生[15]。假设噪声为高斯白噪声[16],数值模拟中按照式(16)在各测点加入高斯白噪声。
xa,n=xa+(xa)maxRns
(16)
式(16)中:xa为无噪声测点a加速度响应;xa,n为有噪声测点a加速度响应;R为随机添加的均值为0、方差为1的数列,模拟测试时的高斯白噪声;ns为人工控制的噪声程度,加入噪声的标准差为该测点加速度幅值最大值的ns倍。
按式(17)计算该测点加速度信号的信噪比:
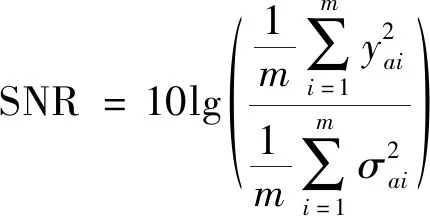
(17)
式(17)中:yai为侧点a第i时间的加速度值;σai为侧点a第i时间点的噪声值;m为时间点数。通过计算信噪比SNR与ns之间的对应关系如图10所示。
由图10曲线可知,SNR随ns的增大而减小,并且在ns=0.243时信噪比为0,说明此时噪声的能量与原始信号的能量相同,导致振动加速度响应的波动性更强,同时掩盖了损伤信号的信息,影响结构的损伤识别效果。加入0 dB的信号对比如图11所示。
为了验证加入信噪比后,该方法的识别精度,在第10号单元损伤时的原始信号中加入信噪比为80、60、40、20 dB的噪声进行分析,其结果如表3、表4所示。表3的损伤位置识别结果表明,60 dB以上信噪比,识别精度在98%以上。表4的损伤程度结果表明,40 dB以上信噪比,识别精度在93%以上。为得到较好精度,选取信噪比高于60 dB的试验环境中,进行实际测试,以保证较好的识别精度。
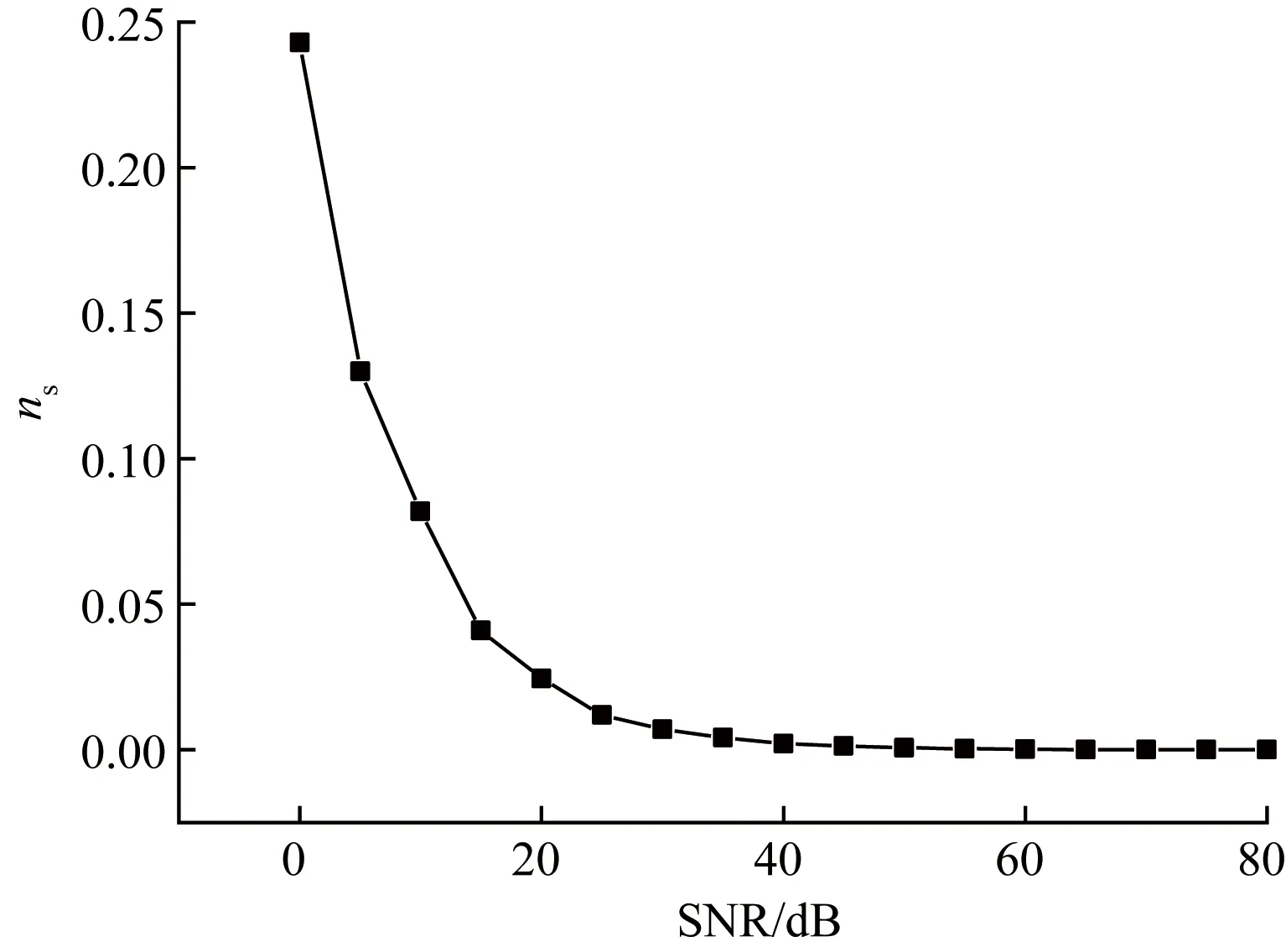
图10 SNR与ns的关系Fig.10 Relationship between SNR and ns

图11 原始信号与加噪信号对比Fig.11 Comparison of original signal and noise signal
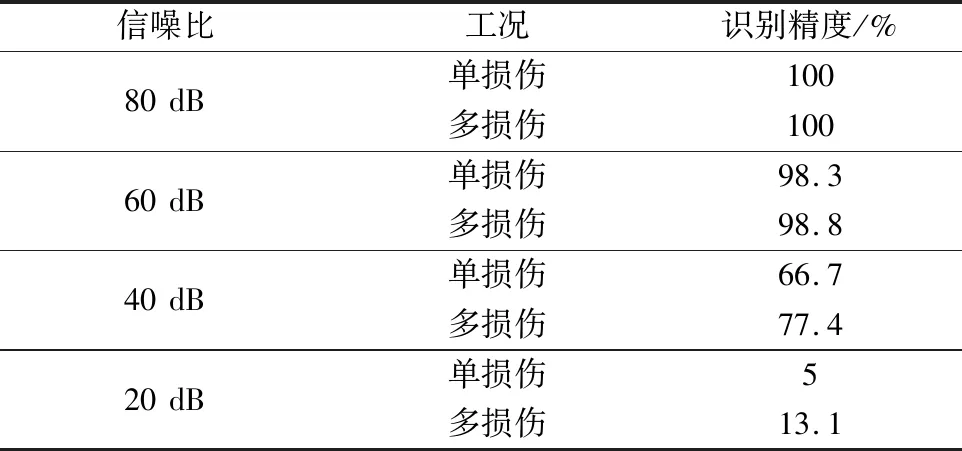
表3 损伤位置识别结果Table 3 Location identification results

表4 损伤程度识别结果Table 4 Damage degree identification results
3 试验模型验证
为了进一步验证在实际工程结构的适用性,在实验室搭建了6层框架模型,如图12所示。框架总高度1.8 m,每层高度0.25 m,梁的长度0.35 m,该框架结构构件采用的钢材型号Q235,其密度7 850 kg/m3,弹性模量为E=2.1×1011Pa,泊松比0.3。
实验结构的损伤方法如下:减小杆件厚度以模拟结构损伤。考虑结构可能的损伤情况,设计拆卸方便的梁、柱损伤工况(表5):①按照框架的损伤位置分为单一单元损伤和多单元损伤;②按照杆件类型可分为柱损伤和梁损伤;③实验中未考虑单元损伤程度的识别。
实验过程中,将横截面尺寸为30 mm×8 mm的杆件作为未损伤,将横截面尺寸为30 mm×6 mm作为损伤杆件,厚度变小导致单元的刚度减小,即表示单元损伤。未损伤及损伤的梁、柱杆件如图13所示。模拟损伤工况过程中,需要对模型的构件进行更换,所以更换构件的节点处采用螺栓固定,忽略螺栓连接对整体刚度的影响。

1~14代表结构测点编号;(1)~(18)代表单元编号图12 6层框架试验模型Fig.12 Six-layer frame experimental model

表5 损伤工况Table 5 Damage condition

图13 损伤杆件示意图Fig.13 Schematic diagram of damaged bar
力锤在12号节点施加水平方向的冲击力,采集8号节点水平方向加速度信号。根据支持向量机对数据集的要求,以及试验误差的影响,每一个工况先后施加20次冲击荷载,采集20组不同荷载下的水平加速度响应信号,其中14组数据作为支持向量机的训练集,用于形成SVM模型,6组数据作为测试集,基于SVM模型进行预测,实现识别的功能。
以第(15)号梁单元单一损伤为例,通过力锤施加激励,施加峰值为120 N的冲击荷载后,采集到的加速度响应信号如图14所示。由于噪声的影响,导致时域信号的复杂度增大,对所有工况的识别效果会产生一定的影响,单一损伤和多损伤工况的识别结果如图15所示。单一损伤的识别正确率为83.3%,多损伤的识别正确率为70.8%。在有限的试验条件下,实现了较好的识别效果。
从单一损伤的识别结果中可以得出,纵坐标标签为2、3的数据分别代表第(3)、(10)柱单元损伤的识别结果,基本能够全部识别,纵坐标标签为4的数据代表第(15)梁单元损伤的识别结果,6个测试数据中只有3个能够识别准确,准确率仅有50%,表明了柱单元的损伤识别准确率高于梁单元。
对于杆件而言,厚度的减小,对弯曲刚度(EI)的影响比对轴向刚度(EA)的影响大。对于本试验设计的结构而言,水平响应主要取决于梁单元的轴向刚度和柱单元的弯曲刚度。因此,在不考虑数据规模的因素的情况下,梁单元的损伤对结构响应的影响比柱单元的损伤要小,在识别梁单元的过程可能会出现偏差,所以导致梁单元的损伤工况比柱单元的损伤工况识别准确率低。
同时,从数值分析中可以得出噪声会降低识别的准确率这一结论,然而对于试验模型来说,噪声的影响无法避免,因此在后面的研究过程中,可以进一步从降噪算法方面改善此方法的应用。
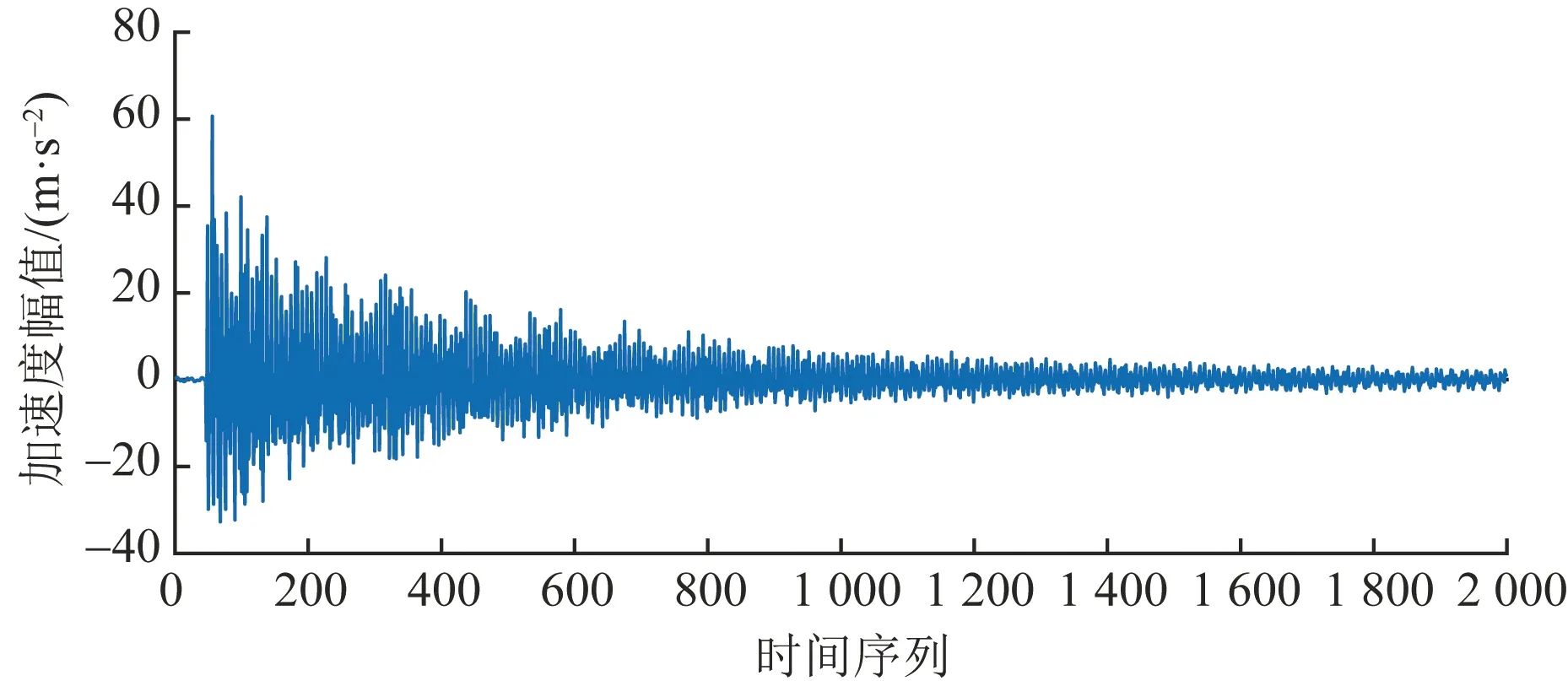
图14 加速度响应信号Fig.14 Acceleration response signal
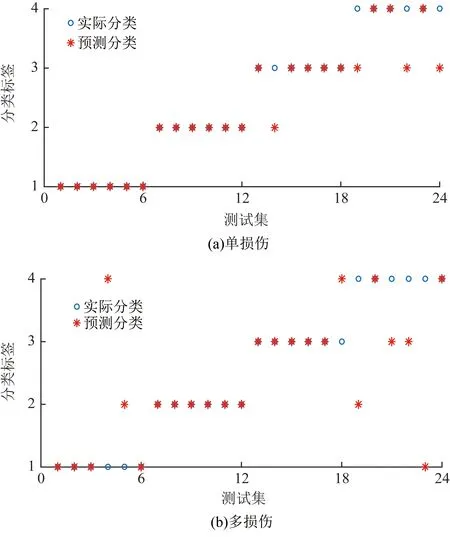
图15 实验损伤工况识别结果Fig.15 Experimental damage condition identification results
4 结论
(1)结合小波包样本熵和支持向量机的识别方法,利用框架结构上某一个测点的振动加速度响应识别整体结构的损伤状态,达到了较好的识别效果。此方法减少了传感器的数量,大大提高了识别效率。
(2)利用小波包样本熵作为损伤指标,不仅可以实现损伤位置的识别,也可以进一步对其损伤程度进行识别。损伤定位识别,需要实测信号的信噪比在60 dB以上,对不同程度的损伤识别,则需要实测信号的信噪比在40 dB以上,以保证识别的结果在90%以上。
(3)试验模型识别结果可知,框架结构中,柱的识别精度大于梁的识别精度,进一步将研究如何降噪、减少梁识别误差、以及开展损伤程度的识别研究工作。
